Stefanica D. Solutions Manual: A Primer For The Mathematics Of Financial Engineering
Подождите немного. Документ загружается.


134
CHAPTER
5.
TAYLOR'S
FORMULA.
TAYLOR
SERIES.
if
the
put
option expires in 1, 3, 5,
10
, and
20
years.
Solution:
The
approximate option values and
the
corresponding approxima-
tion errors are given below:
T
凡
.p
prox
PBS
Error
l 4.1317
4.1491
0
.4
2%
3
5.9834
6.1577
2.83%
5 6
.4
652
6.9714
7.26%
10
5.2187
7.3398
28.90%
20
-2.5067
6.0595
NjA
While
the
approximation formula is still within
3%
of
the
Black-Scholes
value when
the
maturity
is three years or less,
it
deteriorates for long
dated
options,
and
even produces a negative value for
the
20-years
option.
口
Chapter
6
Finite
Differences.
Black-Scholes
PDE.
6.1
Solutions
to
Chapter
6
Exercises
Problem
1: A butterfly spread
is
made of a long position in a call option
with strike
K
一叽
a
long position in a call option with strike
K
十凯
and
a short position
i
口
two
calls with strike
K.
The
options are on the same
underlying asset
and
have
the
same maturities.
(i) Show
也
at
the
value of
the
butterfly spread
is
C(K
十
x)
-
2C(K)
+
C(K
-
x)
,
where, e.g.,
C(K
+
x)
denotes
the
price of
the
call with strike
K
十
x.
(ii) Show
that
,in
the
limiting
cωe
when x goes
to
0,
the
value
of a position in
主
b
耐
er
组
y
spreads as above
co
盯
erges
to
the
second order partial derivative
of
the
value of
the
option, C, with respect
to
strike K ,i.e., show
that
C(K
十
x)
-
2C(K)
+
C(K
-
x)
护
C
=一
τ
(K).
2
、
6
x
2
8K2
(iii) Show
that
,in
the
limiti
吨
case
when x • 0,
the
payoff
at
maturity
of
a
po
副
on
in
~
butte
吻
spreads
as above
is
goi
吨
to
approximate
the
payoff
of a derivative security
that
pays 1
if
the
underlying asset expires
at
K , and
ootherwise.
Note: A security
that
pays 1in a certain
state
and 0
i
丑
any
other
state
is
called
an Arrow-Debreu security
, and its price is called
the
Arrow-Debreu price of
that
state
A position h i butter23rspreads as above7with Z
smll7is
a
synthetic way
to
construct
a
口
Arrow-Debreu
security for
the
state
S(T)
=
K.
Solution: (i)
The
value of a butterfly spread,i.
e.
,of a long position in a call
option with strike
K - x and value
C(K
-
x)
,a long position in a call option
with strike
K
十
x
and value
C(K
+
x)
,
and
a short position
i
口
two
calls with
strike
K
and
value
-2C(K)
is
C(K
+
x)
-
2C(K)
+
C(K
-
x).
135

136
CHAPTER
6.
FINITE
DIFFERENCES.
BLACK-SCHOLES
PDE.
6.1.
SOLUTIONS
TO
CHAPTER
6
EXERCISES
137
(ii)
The
value of a position
in
去
butterfly
spreads is
毛
(C(K
忖)
-
2C(K)
+
C(K
-
x)).
(6.1)
x
..
The
value of a call
option
as a function of
the
strike of
the
option
is infinitely
many
times
differentiable (for any fixed point
i
丑
time
except
at
maturity).
The;efore
the
expression from
(6.1)
represents
the
central
finite difference
approximation
of
在
(K)
and
we
know
山
t
C(K
叫一
2C
(K)
+C(K
-
x)
=
些
(K)
+
O(
泸)
σ
K2
Then
, in
the
limit as x goes
to
0,we
obtain
that
C(K
+
x)
-
2C(K)
+
C(K
-
x)
θ2C
=一
τ
(K).
z\o
x
2
8K2
Problem
2: A bull
spread
is
made
of a long position in a call
option
with
strike K
and
a
short
position in a call option
wi
出的
rike
K +x,
both
options
being on
the
same
underlying asset
and
having
the
same
maturities. Let
C(K)
and
C(K
+
x)
be
the
values
(创
time
t) of
the
call options
with
strikes
KandK
十叽
respectively.
(i)
The
value
of a position in
~
bull spreads is
cmf(K
刊
)In
the
limiting
case when x goes
to
0,show
that
C(K)
-
C(K
十
x)
θC
=一
~;/(K)
z\
",
0 x
θK
QU
)d
nu
e
ihJTL
kd
'+b
…
4EU
-u
an
mi
sn
a--
nuoo
:7;
-I7·1·1·1·IE
DAa
'ue
ne
DT
( 0, if 8 < K - x;
j
仨竖立
1
,
if K - x
::;
8
::;
K;
fx(8)
=
{刑,
--
~-
--
1
互年
-8
,
if
K::;
8
::;
K +
x;
I 0, if K + x < 8.
Note
that
fx(K)
= 1 for any
x
并
0
,
and
therefore
Ii闷儿
(K)
=
1.
z
\>U
(ii) Show
that
,in
the
limiting case when x • 0,
the
payoff
at
maturity
of
a position in ; bull spreads as above is going
to
approximate
the
payoff of a
derivative security
that
pays 1 if
the
price of
the
underlying asset
at
expiry
is above K ,
and
0 otherwise.
Note: A position in
~
bull
spreads
部
above
,
with
x small,is a synthetic way
to
construct a
cash-or-nothing
call
maturing
at
time
T.
Solution: (i) Since
the
value
C(K)
of
a call
option
as a function
of
the
strike
K of
the
option
is infinitely
many
times differentiable,
the
first order forward
且
nite
difference
approxim~tion
~f
~去
(K)
is
θC
C(K
十
x)
-
C(K)
一
(K)
=
一
+
O(x)
,
θK
as x •
O.
We conclude
that
C(K)
-
C(K
十
x)
θC
=一一
(K).
2
、
o
x
θK
(6.2)
(ii)
The
payoff
at
maturity
of
the
bull
spread
is
r 0, if
8
三
K;
max(8
- K ,
O)
-
max(8
一
(K
十
x)
,
O)
={
8-K
,
if
K<8
三
K+x;
, x,
if
K +x <
8.
If
gx(8)
denotes
the
payoff
at
maturity
of a position in
~
bull spreads,
then
r 0, if
8::;
K;
如何)
=
<与互,
if K <
8
三
K+x;
l 1, if
K
十
x
<
8.
If
8
三
K
,
then
gx(8)
= 0 for
any
x > 0
and
therefore
Ii
同
gx(8)
= 0, V
8
三
K.
Z\
。
U
(6
.4)
Let 8
笋
Kbea
直
xed
value of
the
spot
price of
the
underlyi
吨
asset.
Then
儿
(8)
= 0 for any x such
that
0 < x <
IK
-
81
,
and
therefore
li
同
fx(8)
= 0, V 8
并
K.
(6.3)
Z
\人
j
From
(6.2)
and
(6.3)
,we conclude
~hat
,
in
the
limiti
吨
case
when x • 0,
the
payoff
at
maturity
of a position in ;
butterfly
spreads as above is 1 if
the
underlying asset expires
at
K ,
and
0
otherwise.
口

138
CHAPTER
6.
FINITE
DIFFERENCES.
BLACK-SCHOLES
PDE.
6.1.
SOLUTIONS
TO
CHAPTER
6
EXERCISES
139
If
S > K ,
then
gx(S)
= 1 for
a
叮
x
such
that
0 < x < S - K , and
therefore
as
h
→
O.
口
(6.5)
Ii同
gx(S)
= 1, V S >
K.
x \ ,U
From
(6.4)
and
(6.5)
,
we
conclude
th~t
,
in
the
Ii
miti
吨
case
when x • 0,
the
payoff
at
maturity
of a position in
~
bull spreads as above is 1 if
the
underlying asset expires above K ,and 0
otherwise.
口
Problem
4: Find a
centralfinite
difference approximation for
the
fourth
derivative of
f
at
风
i.e.
,
for
f(4)(
α)
,
usi
吨
f(
α
-
2h),
f(
α
-h)
,
f(
α)
,
f(
α
十
h)
,
and
f(
α+
2h).
What
is
the
order of
this
缸
ite
difference approximation?
Solution: We will use
the
following Taylor approximation of
f(x)
around
the
point x =
α:
as h •
O.
We multiply
(6.7)
by 4 and subtracting
the
result from
(6.8)
to obtain
2h
3
f(
α
+
2h) -
4f(
α
+h)
=
-3f(
α)
-
2h
f'(
α)
十了
f(3)(
α)
+ 0
(的,
(6.9)
as h •
O.
By solving
(6.9)
for
f'(
α)
,
we
obtain
the
following second order
缸
lite
difference approximation of
f'
(α):
Problem
3: Find a second order finite difference approximation for
f'(
α)
using
f(
α)
,
f(
α
+
h), and
f(
α
+
2h).
Note: This
type
of approximation
is
needed, e.g., when discretizing a PDE
with
boundary conditions
i
盯
olvi
吨
derivatives
of
the
solution (also called
Robin boundary conditi
∞
s). For example, for Asian
Op
抖
tions
(c
∞
O
丑时叫
t
悦
lnuou
computed
ave
臼
ra
略
ge
rate
call,
to
be
more precise), this
type
of
finit~
_difference
approximation
is
used to discretize
the
boundary
conditio
丑誓+嚣=
0,for
R=O.
Solution: To obtain a finite difference approximation for
f'(
α)
in terms of
f(
α)
,
f(
α
+
h) ,and
f(
α
十
2h)
we
use
the
cubic Taylor approximation of f
(x)
around
the
point x
=
风i.
e.
,
f(x)
=
f(
α)
十
(x
一的
f'(
α)
+(气川
"(
α)
十(气川但)
(α)
十
o
((x
一
α)4)
, (6.6)
as x
→
α.
By
letti
吨
Z
工
α
十
h
and x
=
α
+
2h in
(6.6)
,
we
obtain
that
f(
α
十
h)
十
f(
α
-
h)
=
f(
α
+
2h) +
f(
α
-
2h) =
(x
一
α
)2
II(x
一
α)3(3)
f(
α)
十
(x
一
α
)
f' (α)
十
2
-J
f"
(α)
十
6f()(α)
+(zf
f(4)(
α)
+(
+ 0
((μZ
一
α
叫)
7)
,
(6.10)
f(x)
=
(4)(~\
_
f(
α
+
2h) -
4f(
α
+h)
十
6f(
α)
-
4f( α
-
h)
十
f(
α
-
2h)
f~4)
(α)
_ J
\~
I
-'UJ
~J
\~
I
'UJ
I
~Jh~
十
O(
的?
ash
→
O.
口
Problem
5:
The
goal of this exercise
is
to
emphasize
the
importance of sym-
metry
坦白
nite
difference approximations. Recall
that
the
central difference
approximations for
the
first and second order derivatives are
h
4
_IA\.
, h
6
2f(
α)
+ h
2
f"(
α)
十一
f(4)(
α)+-f(
川的
12
OJ
,--/.
360
十
o
(h
7
)
, as h •
0;
(6.11)
4h
4
_fA\.
, 8h
6
2f(
α)
+ 4h
2
f"(
α)
+
"or:
f(4)(
α)
十一
f(6)(
α)
3
OJ
,--/.
45
十
o
(h
7
)
,
(6.12)
as h •
O.
We
multiply
(6.11)
by 4 and
subtract
the
result from (6.12).
We
solve for
f(4)(
α)
and obtain
the
followi
口
g
second
order
丑
ni
te
difference
approximation:
as
x
一→
α-
For symmetry reasons, and keeping in mind
the
form of
the
central
diι
ference approximation for
f"
(
α)
,
we
use
(6.10)
to compute
h
2
_",'
h
3
_1
飞
A
f(
α)
+
h
f'(
α)+Efff(α)
+
'~
f(3)(
α)
+ 0
(的;
(6.7)
4h
3
川
A
f(
α)
+
2h
f'(
α)+
约
2f"(
α)+
了
f(3)(
α)
+ 0
(的,
(6.8)
f(
α
十
h)
f(
α
+2h)
f'(
α)
一
f(
α
+
2h) +
4f(
α
+h)-3f(
α)
h
2
r
(3)
2h
十';
f(3)(
α)
+ 0
(的
-f(
α
+
2h) +
4f(
α
十
h)
-
3f(
α)2
2h+O
(的?
f'(
α)
f"(
α)
f(
α
+
h)
-
f(
α
-
h)
2h
十
(h
2
)
;
f(
α
+h)-2f(
α)
+
f(
α
-
h)
~~""J
I J \""
'~J
+ 0
(h2)
,
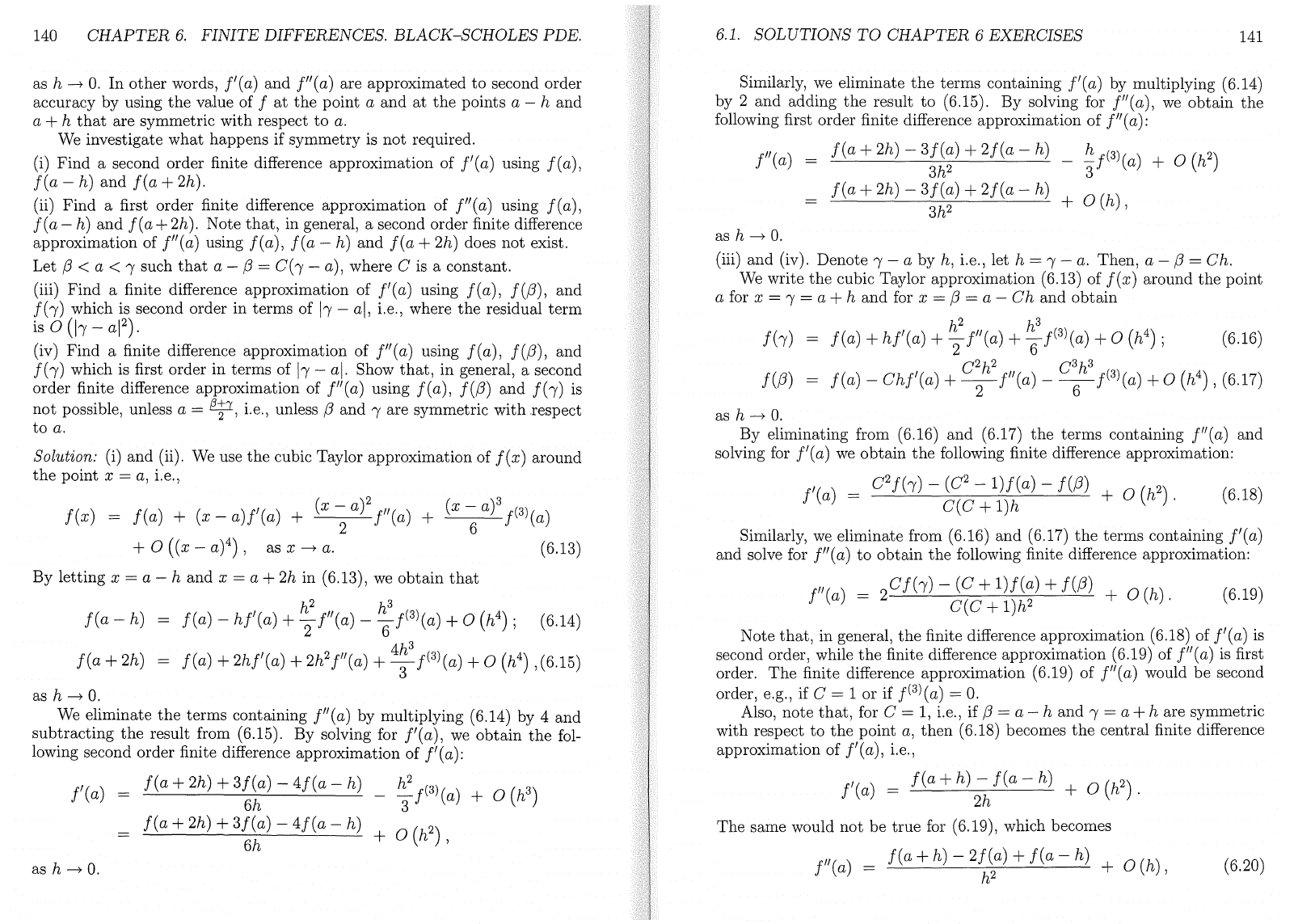
as h •
O.
(iii)
a
时
(iv).
Denote
γ
一
αby
h, i.e. , let h
=
γ
一
α.
Then
,
α-
(3
= Ch.
We write
the
cubic Taylor approximation (6.13) of
f(x)
around
the
point
α
for x
=
γ
=
α
+
h
and
for x
二二(3=
α
-
Ch
and obtain
Similarly
,
we
eliminate
the
terms
containi
吨1'
(α)
by multiplying (6.14)
by 2 and adding
the
result
to
(6.15). By solving for
f"(
α)
,
we
obtain
the
following
负
rst
order finite difference approximation of
f"
(α)
:
f"(
α)
=
f(
μα
+叶州叫
2
孰圳
h
均川)卜一斗3
豆♂扩??俨俨)忡川十叶叫
2
勾附
f
f(
归
α
+ 2h)
一
3f(
归刨
α
叫)
十
2f(
归
α
一
h
川
)
?+O
(h)7
3h
2
as h •
O.
By eliminating from (6.16) and (6.17)
the
terms
containi
吨
f"(
α)
and
solving for
1'
(α)
we
obtain
the
following finite difference approximation:
C
2
f (
'Y)
- (C
2
-
1)
f
(α)
-
f(
(3)
1'(
α)1C(C
十
l)h+O
(的
(6.18)
Similarly,
we
eliminate from (6.16) and (6.17)
the
terms
contai
时日
g
1' (α)
and solve for
f"
(α)
to
obtain
the
following finite difference approximation:
141
(6.19)
h
2
_".,
h
3
f(
α)
+ h
1'
(α)
+
';
f
勺)
+
'~
f(3)(
α)
+ 0 (h
4
) ;
(6.16)
C
2
h
2
_".,
c
3
h
3
_(9
飞
A
f(
α)
-
Ch
1'
(a)
十一
f-
fll(
α)
一
-rf(3)(α)
+0
(的,
(6.17)
Cf(
γ)
一
(C+1)f(
α)
+
f(
(3)
f"(
α)
=
2
十
o
(h).
C(C
十
1)h
2
f(
'Y)
f(
(3)
6.1.
SOLUTIONS
TO
CHAPTER
6
EXERCISES
Note
that
,
i
口
general
,
the
finite difference approximation (6.18) of
f'(
α)
is
second order
,while
the
finite difference approximation (6.19) of
f"(
α)
is
且
rst
order.
The
finite difference approximation (6.19) of
f"(
α)
would be second
order
,e.g., if C = 1 or if
f(3)(
α)
=
O.
Also, note
that
, for C = 1, i.e. , if
(3
=α
-h
and
γ=α
十
h
are symmetric
with respect
to
the
point
α
,
then
(6.18) becomes
the
central finite difference
approximation of
l'
(α)
,
i.e. ,
f(
α
+
h)
-
f(
α
-
h)
1'(
α)=+O
(的
门飞
The
same would not be
true
for (6.19), which becomes
f(
α
十
h)
-
2f(
α)
+
f(
α
-
h)
f"(
α)=79
十 o
(h)
, (6.20)
140
CHAPTER
6.
FINITE
DIFFERENCES.
BLACK-SCHOLES
PDE.
Solution: (i) and (ii).
vVe
use
the
cubic Taylor approximation of
f(x)
around
the
point x
=
矶
i.e.
,
f(x)
=
f(
α)
十
(x
一
α
)
1'
(α)
+
(x
一
α?
f"(
α)
十
(x
一
α)3
f(3)(
α)
2
+ 0
((x
一
α)4)
,
as x
→
α(6.13)
By letting x
=
α
-
h
and
x
=
α
+
2h in (6.13),
we
obtain
that
h
2
rill
\ h
3
f(
α
-
h)
=
f(
α)
-
h
1'(
α)+Eff(α)-lff(3)(α)
+ 0 (h
4
) ;
(6.14)
4h
3
f(
α
+
2h) =
f(
α)
十
2h
1'(
α)
+ 2h
2
f"(
α)
十了
f(3)(
α)
+0
(的,
(6.15)
as h •
O.
We eliminate
the
terms
c
∞
O
丑川
t
创口旧
in
吨
g f"
气
1
(μα)
by
ml
咄
i
毕
pI
趴
y
抖
ri
鸣
(仰
6.14
钊)
b
均
y
4
an
丑
1
su
由
b
忱
tractir
吨
the
resul
忧
t
from
(仰
6.1
臼叫
5
盯).
By solvi
吨
for f'(
α
),
we
obtain
the
fol-
lowing second
order
自
nite
difference approximation of
l'
(α)
:
一
f(
α
+
2h) +
3f(
α
)
4f(
α
…
h)h
2
1'(
α)-6h-Ef(
川
α)
+ 0
(h
3
)
f(
α
+
2h) +
3f(
α)
-
4f(
α
-
h) 2
6h
十
o
(h
2
)
,
as h •
O.
as h •
O.
In
other words,
f'(
α)
and
f"(
α)
are approximated
to
second order
accuracy by using
the
value of f
at
the
point
αand
at
the
pointsα-
hand
α
+
h
that
are symmetric with respect
toα.
We investigate what happens if symmetry is not required.
(i) Find a second order finite difference
approxi
口
lation
of
f'
(α)
usi
吨
f(
α)
,
f(
α
-
h)
and
f(
α
+
2h).
(ii) Find a first order finite difference approximation of
f"
(α)
usi
吨
f(
α)
,
f(
α
-
h)
and
f(
α
+
2h). Note
that
, in general, a second order finite difference
approximation of
f"
(α)
using
f(
α)
,
f(
α
-
h) and
f(
α
+
2h)
does
日
ot
exist.
Let
(3
<α<γsuch
thatα-
(3
=
C(γ
一
α)
,
where C
is
a constant.
(iii) Find a finite
differe
肌
e
approximation of
f'
(α)
四吨
f(
α)
,
f(
(3),
and
f(γ)
which
is
second order in terms of
b
一
αI
,
i.e., where
the
residual
term
isO
(Iγ
一
α1
2
)
(iv) Find
a
直
nite
difference approximation of
f"
(α)
using
f(
α)
,
f(
(3),
and
f (
'Y)
which is first order in terms of
b
一
αI.
Show
that
, in general, a second
order finite difference approximation of
f"
(α)
using
f(
α)
,
f
((3)
and f (
'Y)
is
not
possible
,叫
esMzEFFie?mlessβandγare
sym
皿
etric
with
.r
esp
创
to
α.

142
CHAPTER
6.
FINITE
DIFFERENCES.
BLACK-SCHOLES
PDE.
instead
of
the
central finite difference approximation
f(
α
+h)-2f(
α)
+
f(
α
-
h)
f
协)
=ω
十
O(
的
of
f"(
α).
This
is
due
to
the
fact
that
, for C = 1,
the
coe
自
cient
of h from
o(h)'
f~om
(6.20)
cancels
out
and
the
next
term
of order 0
(的
becomes
relevant.
口
Problem
6: Consider
the
following first order ODE:
y'(x) = Y(x), V
x
ε[0
,
1];
ν(0)
=
1.
(i) Discretize
the
i
且
terval
[0
,
1]
using
the
nodes
Xi
=
ih
, i = 0
:叽
where
h=
去
Use
forward finite differences
to
obtain
the
following
缸
lite
difference
discretization of
the
ODE:
的
+1
=
(1
+
f
仰
i
,
Vi = 0 :
(η-
1)
,
with
yo
=
1.
Show
that
的=
(1
+
f
讥
Vi
=
0:η.
(ii) Note
that
y(x) =
eX
is
the
exact solution of
the
ODE. Let
ei
=
Yi
- Y(Xi) =
(1
+ h)i - e
ih
be
the
approximation error of
the
finite difference solution
at
the
node
Xi
,
i = 0
:η.
Show
that
this
finite difference discretization is convergent, i.e.,
that
lim
J;ll
ftx
I
ei
I =
O.
n
一→。
C
2=U:η
Solution: (i) Recall
that
yo
= 1
and
Y
i+
1 =
(1
十
h)Yi
,
for all i = 0 : (n - 1).
It
is easy
to
see
by
induction
tl
川的=
(1
+}札
for
all i = 0
:η:
Initial
condition: for i = 0,
we
know
that
yo
= 1 =
(1
十
h)o.
Induction
step: assume
that
Yi
=
(1
十
h)2.
Then
,
的
+1
=
(1
+ h)Yi =
(1
+
h)
忡
17
which is
what
we
wanted
to
show.
(ii) Let Y(
x)
=
eX
be
the
exact solution of
the
ODE.
It
is easy
to
see
tl
时
the
approximation error ei
can
also
be
written
as
ei
=的
-
Y(Xi) =
(1
+ h)i - e
ih
= e
i1n
(1+h)
_ e
ih
=
e
仇(
e
i
(l
n(l+h)
6.1.
SOLUTIONS
TO
CHAPTER
6
EXERCISES
143
Using
the
Taylor approximation In
(1
+叫
:Z-4
十
O(X
3
)
we find
that
I I
1.-
2
\\
i ( (
h
一亏十
O(
的)
- h}
h2
1.-
2
-i
亏+
iO(
的工-~亏+
O(
时)
,
s
年
ce
ih
三
1
,
for all i = 0
:ηNote
that
the
estimate
iO(h
3
) =
O(h
2
) is
sharp
,since, for i
=叽
the
product
ih
is equal
to
ih
=
nh
=
1.
From
the
Taylor approximation
eX
=
1
十
X
+
O(x
2
)
,
it
now follows
that
i
(l
n
(1
+
h)
-
h)
ei
[ln(l
十
h)-h]
_ 1
\1llI/
\l/
qA
h
o
-mb
/IlI-\
//II11\
4t4
-o
-+
\1111/\lll/
/lit\/iil\2-
since
ih
三
1
for all i = 0
:η
,
and
therefore
'hM
\Ill-/
vhM
O
'h-2
/III-\
/It--1\
\11llI/
\1111/
\,
IJ
vhM
-nb
,
/Il--1\
/JIll-\
Since e
ih
< e for all i = 0 : n, we
obtain
that
回
iq | =
jE
臼眈
2
盟野
g
窍
3
l
卡
e
i
仇
h
(←
μ
伊
e
i
(
川沪
i(
呻巾
(1
队忡
in
::;
e
~~~
lei
(ln(l+h)-h)
-
11
1.-
2
<e
i22
号
I-i
亏
+O(
的|
<已;十
O(h
2
)
咐=
o(~)
We conclude
that
lim
J;ll
ftx
I
ei
I - 0,
n
一→。
o
2=u:n
and
therefore
that
the
finite difference discretization scheme of
the
ODE
is
convergent.

145
From
the
boundary conditions (6.22),
we
find
that
Yo
= 1
a
时
Un=i
(ii)For
n=67tkeaIlite
difemme
dberetizatiOII(624)of
tke
ODE
(621)
can be written in
matrix
form as
SOLUTIONS
TO
CHAPTER
6
EXERCISES
6.1.
where A
is
a tridiagonal 5 X 5
matrix
given by
一
(6i
2
-
1)
,
3i
2
十乞
3i2-j7
b
,
AY
i
=
1 :
5;
i
=
2:
5;
i
=
1 :
4
,
VVVVVV
A(i
,
i)
A(i
,
i-1)
A(i
,
i
十
1)
\illit--/
口
Pro
blem
8:
Show
that
the
ODE
=
0
f(x
,
Y(x))
,
Z
Y
\Iil/
of
/IIiI\
‘
f(x
,
Y(x))and
(削)
Y(X)
where
Solution: Note
that
y"(x)
=
2y'(x)
-
x
2
y(x).
Then
,
口
(UZj)z
(勾
fdt2U(Z))
(工
2;)(38)=(
工
2
n
Y(x)
Y'(x)
FINITE
DIFFERENCES.
BLACK-SCHOLES
PDE.
Note
that
we
actually
showed
that
the
finite
difference
discretization
is
first
order convergent
,
i.
e.
,
=
°G)
CHAPTER
6.
144
口
233|eii
(6.21)
(6.22)
Problem
7: Consider
the
following second order
ODE:
\I
x
ε[0
,
1];
-
0
,
3x
2
y"(x)
-
xy'(x)
+
y(x)
的
)=1;U(hj
0
0
25.5
-95
77.5
I.
e.
,
-5
13
O
O
O
Y
b
=
,
}qovhu
1iqAqOAUZWO
UUUUU
/IEt--11111\
A
(i)
Partition
the
interval
[0
,
1]
intoηequal
intervals
,
corresponding
to
∞
des
Xi
=
ih
,
i
=
0
:凡
where
h
=
土.
Write
the
finite
difference discretization
n
of
the
ODE
at
each
node
Xi
,
i
=
1
:
(η
…
1)
,
usi
吨
central
丑
nite
difference
approximations for
both
y'
(x)
and
y"
(x).
(ii)
If
n
=
6
,
we
find
,
from
the
boundary conditions
,
that
Yo
=
1 and
y6
=
~.
The
直丑
ite
difference discretization scheme presented above
will
have
自
ve
equations can
be
written
as a
5
x
5 linear system
AY
=
b.
Find A
and
b.
Solution: (i)
Let
Xi
=
仇,
i
=
0:
凡
where
h
=
~.
We
look for
Yo
,
y1
,
.
..,仇
such
that
yi
is
an
approximate value
of
y(Xi)
,
f6'r
all
i
=
0
:η-
By writing
the
ODE
(6.21)
at
each interior node
Xi
=
ih
,
i
=
1 :
(η-
1)
,
we
obtain
Vi=l:(η-
1).
(6.23)
We
substitute
the
second order
central difference approximations
for
Y"(Xi)
and
y'(
均),
respectively
,
i.e.
,
nu
3X;Y"(Xi)
-
xiy'(Xi)
+
y(Xi)
2y'(x)
十
x
2
y(X)
Y'(X)
y"(X)
can
be
written
as
-
2Y(Xi)
+
y(
向一
1)
2
h2+0(hzh
y(X
i+
1)
-
y(
叫一
1)
2
+
O(
的
7
2h
y(X
i+
1)
ν
"(Xi)
Y'(Xi)
into
(6.23)
,
use
the
approxi
血
a~e
values
yi
for
the
exact values
y(Xi)
,
for
i
=
0
:叽
and
ignore
the
O(
h'
2)
term.
The
followi
鸣
second
order finite
difference discretization of
(6.21)
is
obtained:
UU
+
Uu-
'h
q&
-
0
,
(
3i'
一
DYi
十
1
=
0
,
Vi
=
1
:
(n-1)
叫
十的
UU
'hM
since
Xi
=
ih
,
which
can
be written
as
(3
叶)的一
1
一
(6i
2
-1
如

146
CHAPTER
6.
FINITE
DIFFERENCES.
BLACK-SCHOLES
PDE.
Problem
9: Consider a six months plain vanilla European call option with
strike
18
on
a non-dividend-paying underlying asset with spot price 20. As-
sume
that
the
asset has lognormal distribution with volatility 20% and
that
interest rates are constant
at
5%.
(i) Compute
the
Greeks of
the
call
optio
凡i.
e
,
~,
f , P,vega, and
8.
Use finite differences
to
丑 nd
approximate values for
the
Greeks. Recall
that
A
θCθ2CρθC
一一一:
f
=一一·
ρ
一一一
…一
一
θ
S'
θ
S2'
t'
θγ7
δC
_
vega
-τ
一;。
。
σ
θC
θT
Denote by C
(S
,K ,
T
,
σ
,
r)
the
value of
the
call option obtained from
the
Black-Scholes formula.
(ii)
The
forward and central difference approximations
~f
and
~e
for
~,
and
the
central difference approximation f e for
fare
~f
=
C(S
十
dS
,
K
,
T
,
σ
,
r)
-
C(S
,
K
,
T
,
σ
,
r)
-
f =
dS
~e
=
C(S+dS
,
K
,
T
,
叽
γ)
-
C(S
-
dS
,
K
,
T
,
σr);
一
2dS
f
e
=
C(S+dS
,
K
,
T
,
σ
,
r)
一
2C(S
,
K
,
T
,
σ
,
r)
+
C(S
-
dS
,K ,
T
,
σ
,
r)
一
(dS)2
Compute
the
approximation errors for
the
following values of dS:
dS
6.
f
6.
e
f
e
1
6.
-
6.
fl
1
6.
-
~el
If
- fel
0.1
0.01
0.001
0.0001
0.00001
0.000001
(iii) Let
d
σ=
0.0001
,价=
0.0001,
and
dT
= 在,
i.
e.
, one day. Find
the
following forward difference approximations for
vega
,
ρ
,
and
8:
vegaf
C(S
,
K
,
T
,
σ
+d
σ
,
r) -
C(S
,K ,
T
,
σ
,
r)
dσ
C(S
,K ,
T
,
σ7
俨十
dr)
-
C(S
,K ,
T
,
σ
,
r)
dr
C(S
,K ,T +
dT
,
σ
,
r)
-
C(S
,
K
,
T
,
σ
,
r)
dT
(6.25)
(6.26)
(6.27)
Pf
8
f
6.1.
SOLUTIONS
TO
CHAPTER
6
EXERCISES
147
Solution: (i)
Usi
吨
the
formulas for
the
Greeks of a plain vanilla call option
derived from
the
Black-Scholes formula,
we
find
that
~
= 0.839523; f = 0.086191; P= 7.045377;
vega = 0.01501; 8 =
-1.
394068.
(ii)
The
Blac
k-
Scholes value of
the
call option
is
C = 2.699703.
The
corre-
sponding forward and central difference approximation errors for
the
Delta
and
Gamma
of
the
option are:
dS
6.
f
6.
e
f
e
I~-~fl
I~-~el
If
- fel
0.1 0.843774 0.839464
0.086199
0.00425158 0.00005840
0.0000081~
0.01 0.839952
0.839521
0.086196
0.00042959 0.00000138 0.0000042:
0.001 0.839565
0.839522 0.086195
0.00004228 0.00000082
0.0000042l
0.0001 0.839526
0.839522 0.086196
0.00000349
0.00000081
0.0000042!
0.00001 0.839522 0.839522
0.086207
0.00000037
0.00000081 0.0000153
0.000001 0.839522 0.839522
0.090594
0.00000076
0.00000081 0.0044029
(iii)
The
且由
e
difference approximations of vega,P
and
8
give
川
y
(6.25-6.27)
are
vegaf
3
.4
48385;ρ
f
= 7.045624; 8 f = -
1.
392998.
The corresponding relative approximation errors are
nL
nunununu
--
reJ-
e-
Ip- Pfl
一一一一一
= 0.000035;
p
18
一
8fl_
n
nnn7
C::
巧内
181
…-
Problem
10: Show
that
the
value of a
plai
口
vanilla
European call option
satis
直
es
the
Black-Scholes PDE. In other words, show
that
θC
1
叮叮
θ2C
δC
一
+
';a
2
S
2
一丁
+(γ
-
q)S
一
-
rC
- 0,
θ
t
' 2-
~
8υθS
where C = C
(S
,t) is given by
the
Black-Scholes formula.
Solution: Although direct computation can be used
to
show this result,
we
will use
the
version of
the
Black-Scholes
PDE
invol
飞
ring
the
Greeks, i.e.,
@+jd
价十
(γ
一仙一
rC
0,

148
CHAPTER
6.
FINITE
DIFFERENCES.
BLACK-SCHOLES
PDE.
substitute
for
.6.,
rand
e
the
values
ρ
-q(T-t)
d~
.6.
= e-q(T-t)
N(d
1
);
r-L
e-T-
Sσ
、
/2
作
(T
-
t)
σ
Se-q(T-t)
d~
e - qSe-q(T-t)
N(
d
1
) - rK e-r(T-t)
N(
d
2
) _
~
v
~~G
/~
.,
e-~
,
2 、
/2
作
(T
…
t)
and
substitute
for C
the
value given by
the
Black-Scholes formula, i.e.,
C -
Se-
旷
-t)
N(d
1
) -
Ke-r(T-t)
N(d
2
).
Then
,
@+jd
付
+
(r
…仙一
γc
qSe-q(T-t)
N(d
1
) - r
Ke-r(T-t)
N(d
2
)
σ
Se-q(T-t)
-21
2 飞
/2
作
(T-t)e2
十
σ
2s2
e-q(T-t)
一手
2
S
σ
、
/2
作
(T
-
t)
十
(r
一仙一
q(T-t)
N(d
1
)
一
r(
仇旷
v
川一吁呗
q
创
(T
阳叫
Tι
归叫一→卅
t
功
)N(
μd
出廿
1
0
队.口
Problem
11:
The
value
at
time t of a forward contract struck
at
K and
maturing
at
time T ,on
an
underlying asset
with
spot
price S paying dividends
continuously
at
the
rate
q,is
j(S
,t) = Se-q(T-t) -
Ke-r(T-t).
Show
that
j(S
,t)
satis
五
es
the
Black-Scholes
PDE
, i.
e.
, show
that
θ
j
I 1
_202
θ
2j
δf
百
+
~O'~S:
~a;2
+
(γ
-
q)S
页
-
rj
=
O.
Solution:
It
is easy
to
see
that
红
=
aSe-q(T-t) - rK
e-r(T-t)
坐
θ
t
":1--
.---
,
θS
e-q(T-t);
θ2
j A
θ
S2
-
Then
,
rlu
T
fJ-S
T
rff-qa
AU-nAU
oa
nL
1-2
w-a
6.1.
SOLUTIONS
TO
CHAPTER
6
EXERCISES
149
qSe
一矿
-t)
_
rKe-r(T-t)
+ 0 +
(γ
-
q)Se-q(T-t)
一
γ
(Se-q(T-t)
-
Ke-
r
叫)
O.
口

150
CHAPTER
6.
FINITE DIFFERENCES. BLACK-SCHOLES PDE.
6.3.
SOLUTIONS
TO
SUPPLEMENTAL EXERCISES
151
2.
Let
r
c
~c
6.2
Supplemental
Exercises
1.
Let 1(x) =
x
3
♂
-6
♂.
Show
that
the
central
differe
肌
e
approximation
for
l'
(x)
around
the
point 0 is a fourth order
approximatio
泣
C(K
十队
T)
-
2C(K
,
T)
+
C(K
- x,
T)
1(S)
=
x
2
where, e.g.,
C(K
,
T)
denotes
the
value of a plain vanilla call option
with strike
K and
maturity
T on an underlying asset with spot price
S following a lognormal distribution. Show
that
, for any continuous
function
g :
JR.
•JR.,
户。
c
Ii玛
I
1(S)g(S)
dS
= g(K).
Z\U
I
可出~
J-OC
4.
Consider a six months 5%
in-the-money
plain vanilla European call
option with strike
30
on an underlying asset with volatility
20%
,paying
dividends continuously
at
a
2%
rate. Assume
出
at
the
interest rates are
constant
at
5
%.
(i) Use central differences to compute
the
finite difference approxima-
tions
~c
and r
c
for
~
and
r, respectively, i.e.,
C(S
十
dS)
-
C(S
- dS)
2dS '
C(S
+ dS) - 2C(S) +
C(S
- dS)
(dS)2
for
dS
=
10-
2
with
i-I
:
12
, where, e.g.,
C(S
+ dS) =
C(S
十
dS
,
K
,
T
,
σ
,
r)
denotes
the
Black-Scholes value of
the
call option corre-
sponding
to
a spot price
S
十
dS
of
the
underlying asset.
1
+σ
2S2
r(C)
十十二一
2
8(C)
(ii) Compute
the
Delta and
Gamma
of
the
call using
the
Black-Scholes
formula
, and
the
approximation errors 1
~c
-
~
1
and
Ire
- r
I.
Note
that
these approximation errors stop improving,or even worsen, as dS
becomes too small. How do you explain this?
6.3
Solutions
to
Supplemental
Exercises
Problem
1: Let 1(x) = x
3
e
x
-
6e
X
•
Show
that
the
central difference ap-
proximation for
1'(
x)
around
the
point 0 is a fourth order approximation.
Solution: Recall
that
,in general,
the
central difference approximation of
the
first derivative is a second order approximation, i.e.,
1
'T
N'(d2)
1+
~
~一
-~μ
2r
/T
习
N(d
2
)
(ii)
If
q = 0
but
r
并
0
,
show
that
σ
2S2
r(C)
1
十一一一·一一一
2
8(C)
3.
(i) Show
that
the
approximate formula
(J
2S2
r
1
十二一-.一目
0
2 8
connecting
the
r and
the
θof
plain vanilla European options
is
exact if
the
underlying asset pays no dividends
and
if
the
risk-free interest rates
are zero.
In
other words,for, e.g., call options,show
that
,if r = q = 0,
then
(iii) Consider a six months plain vanilla European call option on
an
underlying asset with spot price
50
and volatility 30%. Assume
that
the
interest rates are constant
at
4%.
If
the
asset pays no dividends,
compute
σ
2S2
r(C)
1 +
一一一-
.一一一
2
8(C)
if
the
options are
at-th
e-
money, 10%,
20%
, 30%, and
50%
in-the-
money, and
10%
,
20%
,
30%
, and
50%
out-of-the-money
, respectively.
What
happens if
the
asset pays dividends continuously
at
a
3%
rate?
f(h) -
f(-h)
2
1'
(0)
= J
\'''/
2~
\ '''/ + 0 (h
2
)
,
as
h •
O.
(6.28)
To see why
, for
the
function f(x) = x
3
e
x
-
6e
气
the
central difference
appro
均
nation
for
l'
(x)
around
the
point 0
is
a fourth order approximation,
we
investigate how
the
approxi
日
lation
(6.28) is derived.
The
Taylor approximation of f (x) around
the
point 0 for n = 5
is
f(x) =
f(O)+x
1'
(O)+
旦
f"(O)
十
21f(
川
0)
+马队
)(0)
+主严
)(0)
2 J \ - / ' 6 J \ - I '
24
J \ - I ' 120
+ 0
(x
6
)
,
as
x•
O.
(6.29)

152
CHAPTER
6.
FINITE DIFFERENCES. BLACK-SCHOLES PDE.
6.3. SOLUTIONS
TO
SUPPLEMENTAL EXERCISES
where, e.g.,
C(K
,
1
寸)
denotes
the
value of a plain vanilla call option with
strike
K and
maturity
T
on
an underlying asset with
spot
price 8 following
a lognormal distribution. Show
that
,for
a
口
y
continuous function 9 :
~
→~,
We let x = h and x =
-h
in (6.29) and sum up
the
two resulting formulas.
After
solvi
鸣
for
1'
(0)
we
obtain
1'
(0)
=f(h)
-
f(
-h)
一句句
(0)
-
1~:f(5)(0)
+ 0
(的,
(6.30)
2h
6"
\ / 120
as
h •
O.
For f (x) = x
3
eX
-
6e
x
,
we
find
that
f(3)
(x) = (x
3
+
9x
2
十
18x
)e
X
,and
thus
that
f(3)(0) =
O.
Also, f(5)(0) =
54
乒
o
and
(6.30) becomes
f(h) -
f(
-h)9h
4
f(h) -
f(
-h)
ff(0)=2h-35+O
(问
:2h+O
(的?
as h •
O.
In
other words,
the
central difference approximation for
f'
(x)
around
the
point 0
is
a fourth order
approximation.
口
where
we
used
the
s
巾的
itutions
z =
8
一
(K
-x)
and
ω
=K+x
two integrals above,
respecti
飞
rely.
Let z =
xy
a
丑
dω=
xt.
Then
dz = x
dy
,
d
ω
=
x dt,
and
we
find
that
1:
f(S)g(S)
dS
=
l'扑
1'
yg
We let x
\、、
o
i
阳
n
(仰
6.3
臼
2
勾)
. Since
the
function 9 :
~
→~
is continuous,
we
obtain
that
炖时
fι:
贝阴川
S
冈归
)g
川
8 =
9
以州(仪川
K
which
is
what
we
wa
时
ed
to show;
ef.
(6.31).
For
the
sake of completeness,
we
provide rigorous proof of
the
fact
that
(6.32) becomes (6.33) when
x
\
¥
O.
To do
so
,
it
is
eno
吨
h
to
show
that
炖叫才
1'
yg
νω
川
g
Let
ε>
0 arbitrary. Since 9
is
continuous,
it
follows
that
there exists 6 > 0
such
that
Ig(K) -
g(7)1
<
εfor
all 7such
that
IK -
71
<
6.
Let x
ε(0
,
6)
and y
ε(0
,
1).
Then
jK
一
(K
-x
十
xy)
I = x(1 - y) < 6
and
therefore
Ig(K) -
g(K
- x
十
xy)1
<
飞
\:j
0 < x < 6, 0 < y <
1.
Therefore,
it
is easy
to
see
that
,for any 0 < x < 6,
l
1'
yg
νωg
川
+忖叫叫♂均
ωUω
忡
)d
<Jlydu=i
In other words,for any
ε>
0 there exists 6 > 0 such
that
l
1'
yg
川
+
xy) dy -
g(K)
1
1
y d
Y
! <
~,
V 0 < x < 6
Then
,by definition,
划
1
1'
yg(K
一叶
xy)
dy
-
g(K)
l'
y
叫=
0
口
(6.31)
~!!J
1:
f(S)
川
8
= g(K)
C(K+
民
T)
-
2C(K
,
T)
+
C(K
- x,
T)
x
2
f(8)
主
(ω(8
一
(K
一川
-2
日
lax(8
一
K
,
O)
+max(8
一协叫,
0))
。…三
K-x;
旦在纯
,
ifK-x<8
三
K;
qiifk<S
三
K+x;
Solution: From
the
definition of
f(8)
,
it
is
easy
to
see
that
f(8)
=
Problem
2: Let
Then
,
汇
f(8)g(8)d8
r
K
S
一
(K
-
x)r
K
+
x
K
十
x-8
儿
-X
泸州
)d8
+
儿泸州
)d8
主
1"
zg(K-x
十忡十刊
ω
g(K
十
Z
一
ω
)d
ω7
Problem
3: (i) Show
that
the
approximate formula
σ28
2
r
l
十一一一·一用。
2 e
