Stefanica D. Solutions Manual: A Primer For The Mathematics Of Financial Engineering

We will show

that

, for

allη;

三

0

，

Yn

十

1

>νnand

Yn+1

<

l.

Note

that

, by

de

且

nition

(33),

Yn

> 0 for all

η

三

O.

Then

,from (33),

it

is

easy

to

see

that

Yn+1

>

Yn

仁斗

(α2

十

I)Yn

十

α>αd+Uη

仁斗

α(ν;

一

α

Yn

- 1) <

O.

(36)

From

(35),

and

using

the

assumptio

且

that

Yn

< l,

it

follows

that

/d

可

4-a

\

Y~

一

αun-1=(un-J)(r2)<O

(37)

Eom(36)and(37)pwe

comiude

tht7if

yn<L

ttm

un+1

>

Um

for

any

η>

O.

From

(33),we

also

在 nd

that

with

Zo

=

年It

is easy

to

see

that

Zn

=

X2

叫

for

all

n

三

0

As expec'ted,

the

sequence

(zn)n

三

o

is decreasing

and

h

部

limit

equal

to

l.

The

prooffollows

by

induction: assuming

that

Zn

> l,we show

that

Zn+1

<

Zn

and

Zn

礼

>

l.

This

proof

is very similar

to

that

given above for

the

seque

丑

ce

(Yr

山三

o

and

is left

to

the

reader

as

an

exercise. We conclude

that

0.3.

SOLUTIONS

TO

SUPPLEMENTAL

EXERCISES

15

(40)

口

lim

X2n

十

1

=

l.

n

一→汉二

lim

Xn

α+

v'歹

τz

im

Xn

- l -

一一一一一

From (39)

and

(40), we find

that

Problem

3: (i)

Find

x > 0 such

that

1V

IATHE

1V

IATICAL

PRELI

1V

IINARIES

14

Yn+1

<

l

白

(α2

+

I)Yn

十

α<α

lYn

十

J

白

Yn

<

α217L1

=

l;

(

指)

XX"

2.

(41)

白叫It

-

I)

(It

+咛

-a)

=0

Since h > 0,

it

follows

that

h = l, i.e.,

that

limn

→∞

Yn

= l.

Recall

that

Yn

二

X2n

for

allη;

三

O.

We showed

that

the

subsequence

made

of

the

even

terms

of

(x

阳

7η

仇

1

by

(32), i.e.,

that

一

the

last

equality

can

be

derived as follows:

l-

α

α2

-

al

十

1

=

l

仁中

l

一

α=α

2l

-

al

2

十

l

仁斗

α

(l2

- al - 1) = 0,

where ttle

last

equality is tfle

same

as(34).

We conclude from (38)

that

, if

Yn

< l

,'

then

Yn+1

< l for all

η

主

O.

III

other

words7we showed

by

induction

that

the

seque

口

ce

(Yn)

吨。

giv

by

the

recursion (33)

with

Yo

=

αis

increasi

吨

and

bounded

from above

by

l.

Therefore,

the

seque

口

ce

(Yn)

吃

o

IS

co

盯

ergent.

Denote

by h =

limn

→∞

Yn

the

limit

of

the

sequence

(Yn)n

'2

o.

From

(33)-

and

using

(35)v

,

;;e

obtai~

th~t

J

一

(α2

十

l)h

十

α

《

1

一

αh

十

l

仁斗

α

(lt

一

α

II

- 1) = 0

X

n

十

1

> X

n

牛二中

2Xn/2

> 2

xn

-

I/

2

牛工:>

X

n

>

X

n

一

1

;

(42)

(43)

XXX'

=

b.

ll/l = 2

1

/

2

.

which is equivalent

to

Consider

the

sequence

(x

n

)n

'2

0

with

Xo

= y'2

and

satisfying

the

following

recurSIOn:

X

n

+1

<

2

伫二?

2

xn

/

2

<

2

宇::}

x

n

/2

<

1

仁::}

X

n

<

2.

We conclude

that

the

seque

口

ce

(x

n

)n

'2

0 is convergent.

If

l =

limn

--t∞

X

n

，

then

l =2l/27

(ii)

Find

the

largest possible value

of

x > 0

with

such

that

there

exists a

number

b> 0

with

~V2'

-/2

Y";'

=

2.

Also,

what

is

the

largest possible value of

b?

Solution: (i)

If

there

exists x such

that

(41) holds

true

,

then

x

2

= 2

a

缸

I

丑

l

therefore x =

y'2.

We

are

left

with

proving

that

队

+1

- -/2x

n

_

γrz/27V

71

主

O.

It

is easy

to

see

by

induction

that

the

sequence is increasing

and

bounded

from above by 2,since

(39)

lim

X2n

二

l.

n

一→

α2

Similarly, we define

the

sequence (zn)n

'2

o

by

the

recursion

一

(α2

+ l)zn

+

α

V

η>0

十 α

Zn

十

1

' ,

.v:::-v

,

16

lV

IATHE

lV

IATICAL

PRELIMINARIES

Then

f'

(t)

=

~卜勺丁

77

一

77?γt;J

俨!?于

1

叫

(t)

ex

~?te

that

the

function f (

t)

is

i

肌

reasi

吨

for

t < e

and

decreasing for t >

e.

Therefore?there will be two values of t such

ttlat(43)is

satis

五

ed

，

i.e.,

s

时

l

that

tl/t=21/27OIIe

value being equal

t027and

the

other

OIle

greater tham

Since

zn<2for

a!1n

主

o

and l =

limn

→∞

x

n

，

we

co

口

clude

that

l = 2,

a

缸

an

口

1

therefore

that

x

=

飞

/2

is

the

solution to (41).

(ii)

If

there exists a number b> 0 such

that

xxx·

- b

for a given x > 0,

then

x

b

= b and

the

时

·ore

x =

b

叭

Recall

from

part

(i)

that

the

functiozlfO)=tl/t

has

&Il

absolute maximum

at

t

=e.We

cOBelude

that

Z

二

b

1

/b

三

maxt

1

/

t

_

e

1

/e

自

1 .4

447

，

t>O

and

that

the

largest value of b such

that

the

limit (42) exists

is

b =

e.

口

Chapter

1

Calculus

review.

Plain

vanilla

options.

1.1

Solutions

to

Chapter

1

Exercises

Problem

1:

Compute Jln(x) dx.

Solution: Using integration by

parts

,

we

find

that

J

In

仪

f

户何叫川

d

伽

x

-

x

川叫

In

闻阳峭

n

叫巾刷(仪例

Z

叫)

一

f

户

μZ

叭呻巾喇

(In

倒川

In

以

n

叫(

Z

川巾叫

ln(

忡

n

叫巾(仪仲

Z

Problem

2: Compute J

x

击x)

dx

by using

the

substitution u = ln(

x)

Solution: Let u = ln(x).

Then

du

=

警

and

therefore

J

Xl~(X)

dx

= J

~

du

= ln(lull

=川

x)l)

+

C 口

xln(x)

--

J

Problem

3: Show

that

(ta

阳

a

缸

n

川

lX

叫

)'=1ν/(

巾

C

∞

Oωsx

叫

)2

a

丑

J

1:

丁训

dx

-

町肌

ctω

阳叫

ta

阳

a

缸

I

l+x

Solution: Using

the

Quotient Rule,

we

find

that

(tan

x)'

(:25)f=(sinx

阳

x

- sin x (cos

x)'

(COSX)2

+

(sinx)2l

(COSX)2

(cosx)2

45i

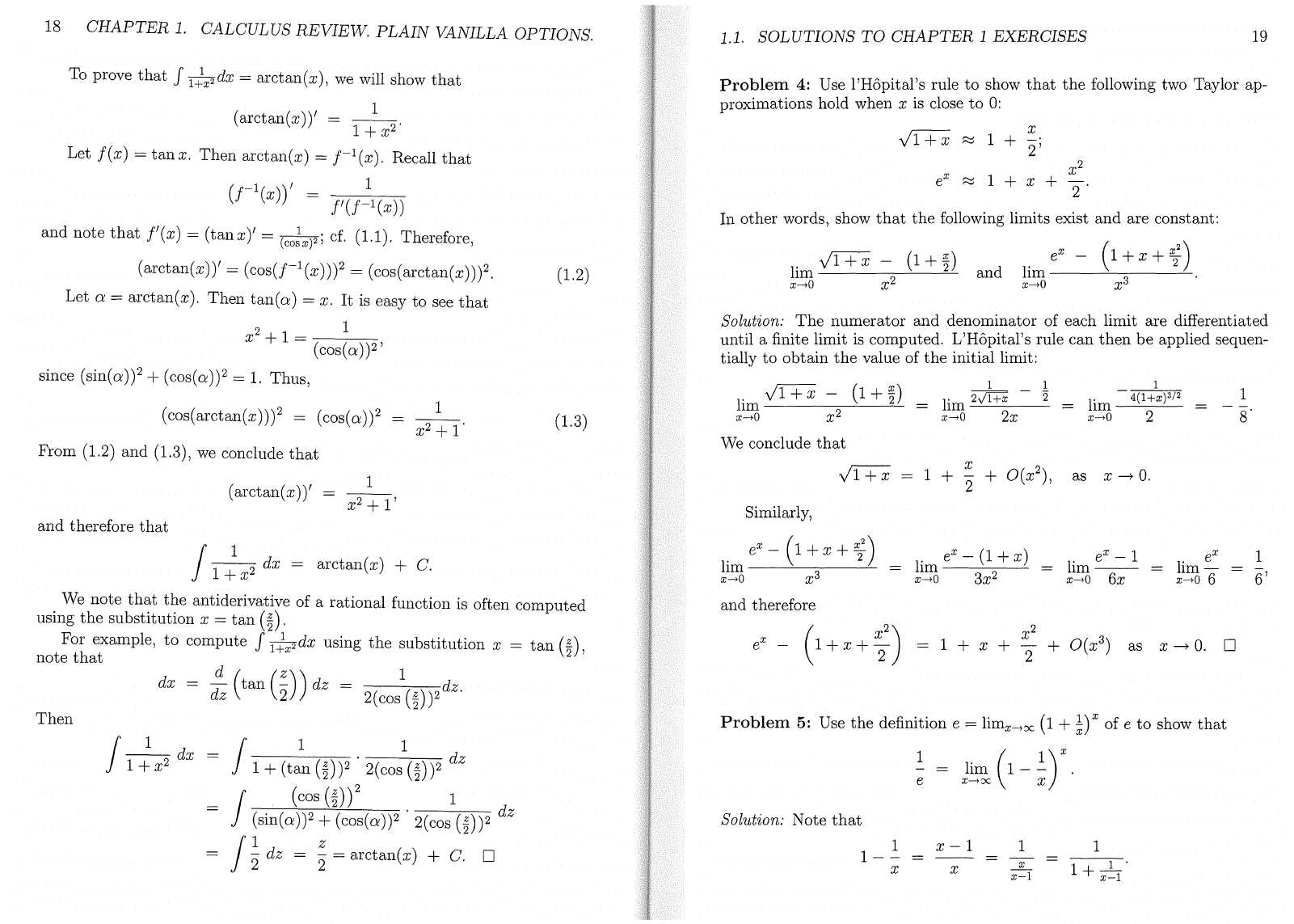
18

CHAPTER

1.

CALCULUS

REVIEW.

PLAIN

~生

NILLA

OPTIONS.

To prove

that

J

1;'x

2

dx

=

arctan(

x)

,

we

will show

that

(arctan(

训

=Jτ

i

十

x~

Let

f(

叫=

tan

x.

Then

arcta

叫

x)

=

f-I(x).

Recall

that

(f-

I

(x))1

= • J

and

note

that

l'

(x)

二

(tanx)'

=讨

x

)2;

c

f.

(1.

1).

Therefore,

(arcta

口

(x))'

= (COS(f-I(X))? = (cos(arctan(x)))2.

Let

α=

arctan(x).

Then

tan(α)=ι

It

is easy to see

that

x

2

十

1=__1

(cos(α)

)2'

since

(sin(α))2

十

(cos(α))2

=

1.

Thus

,

(

cos(arcta

口

(x)))2

=

(co

巾)?

l

x

2

十

1

From

(1.

2)

and

(1.

3)

,

we

conclude

that

(arcta

叫

x))'

and

therefore

that

(1.

2)

(1.

3)

f

市

dx

二

arctan(x)

+ C

We

note

that

tke

antiderivative

of

a rational

fuzlctiOII

is often computed

using

the

Sl

阳

titution

x =

tan

(~)

则

:12Eample?to

compm

j

市

dx

using

the

substitution x

=

阳(~)，

dx

=

~

(tan

(~\飞-

x -

-;-

(

tan

(

~

) ) dz - /

~

\

'"

......

dz.

dz

\-\2))

山

Then

11+

山

~))2

2(

∞

J(5))2dz

f

(∞

S(~))2

1 v

(sin(α))2+(COS(α))2-2(cos(5))2u

I~

d

命

z

= ;

=可

a

叫

n

叫巾(归例

Z

叫)

十

C

口

1.1.

SOLUTIONS

TO

CHAPTER

1

EXERCISES

19

Problem

4: Use I'H6pital's rule

to

show

that

the

following two Taylor ap-

proximations hold when

x is close

to

0:

Jτ

王旬

l+j;

♂自

1

+

x

十二

In other words, show

that

the

following limits exist

and

are constant:

mJ

百三(1

+~)and

liJ-(lfz

呼)

X• o

x'::;

X• o x

Solution:

The

numerator and denominator of each limit are differentiated

until a finite limit is computed.

L'

H6pital's rule can

then

be

applied sequen-

tially

to

obtain

the

value of

the

initialli

皿

it:

1;~

dτ

王一

(1

+~)_

1;

…对古

-i

..…一

汇

;6

x

2

♂巧。

2x

vVe

conclude

that

lim

m• 0

1

8

dτzz

l+i+0(

泸)，

as x • 0

Similarly

,

eX

-

(1

十

Z

十豆}

lim

、/

X• o x

lim

eX

一

(1

+

x)

z• 6

3x

2

lim

eX

- 1

1

日

1

一一一一

m• o

ox

~X

lim

二

X• o h

l

6'

eX

一

(1

十

Z

十二)

1 + x 十二十

O(

内部户。口

Problem

5: Use

the

definition e =

limx

-t

χ(1

+

~)X

of e

to

show

that

\1llI/

1-z

/IIiI\

1IZ

--

1-e

Solution: Note

that

1

一

Z

x-I

1

1+

击

Z

z

x-I

20

CHAPTER

1.

CALCULUS

REVIEW.

PLAIN

VANILLA OPTIONS.

The

口?

\Iiil/

l-z

1i3

IH

Z-z

hhkh

e

1

Sl

日

ce

lim1+_

1

_. _ 1

z

→∞

x-I

and

J

马

(1

+击

r

一

=J414

♂

e.

口

Problem

6:

Let

K ,

T

，

σand

r

be

positive

constants

,

and

define

the

function

g :

lR

•lR

as

g(x) =

~左

i

七言

l(X)

叫协刷(仰例♂叫

V)

wh

阳

1

Solut

刮

4

切

on:

Recall

that

UU

Vd

rJ

31j

ftm

f(b(x))b'(x)

-

f(

α

(x

))α

'(x).

Therefore

,

g'(x)

-Lp

一鸣垣

.

J/

(

川一

1

凸-O-~

(

(b(x))2

飞

而

V

υ

川-y12在叭叭一←厂/

1

eXD

(一

(In

(去)十

(r

十号

)T

门内

飞

12

7f

T

.L

\

2σ

2T

I'

~

xcrVT

Problem

7: Let

f(x)

be

a

contin

∞

us

function.

Show

that

出去

ffz

川

1.1.

SOLUTIONS

TO

CHAPTER

1

EXERCISES

21

Solutio

衍

Let

F(x)

=

J

f

(x)

dx

be

the

antiderivative

of

f

(x).

From

the

Fundamental

Theorem

of

Calculus

,

it

follows

that

fα

+h

F(

α

+

h)

-

F(

α

-

h)

n~_

I

f(x)

dx

=

2h

J

α-h

2fz

Using

I'H6pital's rule

and

the

fact

that

F'(x)

=

f(x)

,

we

find

that

fα

+h

F(

α

+

h)

-

F(

α

-

h)

n~

I

f

(

x)

dx

=

FII!

h

•

62h

J

α

-h

-

,

h

•

6

2h

lim

f(

α

+

h)

+

f(

α

-

h)

h

•

o

2

f(

α)

，

since

f

(x) is a

continuous function.

Note: Let

F(t)

=

J~

f(x)

dx.

The

central finite difference

approximation

of

F'(

α)

is

F(

α

+

h)

-

F(

α

-

h)

2

F'(

α)

=

.L

\'""

I

I~)

2h

.L

\'""

I~)

+

0

(h

2

)

,

(1.

4)

as h

•

o

(if

F(

剖

(t)

=

fll(t)

is

contin

∞叫.

Since

F'(

α)

=

f(

α)

，

formula

(1.

4)

can

be

written

as

1

I'

α

十

h

f(

α)

=

i

二

I

f(x)

dx

+

O(h

2

).

口

2h

J

α

-h

Problem

8:

Let

f

:

lR

•lR

given

by

的)

=

LCi

e

呐?

where

Ci

and

ti

,

i

=

1

:叽

are

positive

constants.

Compute

f'

(y)

and

f"

(y).

Solution:

Note

that

(

e-

yti

)'

e

AFU

NU

U·t

-,

?-b

=t?e-Uti

-tte-uta;

The

丑

7

n

f'(y)

=

-

L

Citi

e

一队;

i=l

n

f"(y)

=

LCi

中

-yti

口

i=l

22

CHAPTER

1.

CALCULUS

REVIEW.

PLAIN

VANILLA

OPTIONS.

Note:The

fmction

f(u)represents

the

price

ofa

bond

with

caskHOWS

Ci

paid

at

time

tt

as a function of

the

yield U

of

tfle

bond.WheIlscaled

appropztate1377

the

丑

rst

and

second derivatives of f

(y)

吼叫

1

respect

to

y give

the

duration

and

convexity of

the

bond

,respectively.

Problem

9: Let f :

JR3

•

JR

given by

f(x)

= 2xr -

XIX2

十

3X2

均

-

x~

，

where

x =

(Xl

,

X2

,

X3).

(i)

Compute

the

gradient

and

Hessian of

the

fur

时

ion

f

(x)

at

the

point

α=

(1

,

-1

,0), i.e., compute

Df(l

,

-1

,

0)

and

D2f(1

，

一

1

，

0).

(ii) Show

that

刷工川的

+Df(

仲

Here

，叽

α

，

and

x

一

αare

3 x 1 column vectors, i.

e.

,

1in

,,"

ZZ

//iz--\

Z

\Illi--/

-i1inu

//11111\

=

\It--/''

ZZZ

Z

Note:

Formul~

(1.

5)_

,is,

the

quadratic

Taylor approximation of

f(x)

around

the

pointαSin~e_

!(x) is a second order polynomial,

the

quadr~tic

Taylor

approximation of

f(x)

is exact.

Solution: (i) Recall

that

Df(x)

(θfθfθf)

瓦

(x)

瓦

(x)

瓦(叮

(

4X

l -

X2

, -

Xl

+

3X3

,

3X2

-

2X3)

;

在

(x)

忐

(x)

忐

(x)

品

(x)

~(x)

蔬

(x)

I =

\11111/

//11111\

D

2

f(x)

Then

,

f(

α)

Df(

α)

f(l

,

-1

,0) = 3

D

f(l

,

~1

，

0) =

(5

, - 1, - 3);

的

(1

，

-1

←(一

;-i

e-;)

(1.

6)

(1.

7)

(1.

8)

D

2

f(

α)

1.

1-

SOLUTIONS

TO

CHAPTER

1

EXERCISES

23

(ii)

W~

substitute

the

叫

ues

from

(1.

6)

,

(1.

7)

and

(1.

8)

for

f(

α)

，

Dt(

α)

~nd

D

2

f(

α)

，

respectively, in

the

expression f

(α)

+

Df(

α

)

(x

一

α)

+ 1

(x

一

α

)t

D

2

f(

α

)

(x

一

α)

and

obtain

that

f(

α

)

+Df(

α

)

(x

一

α)+1(z

一

α

)t

D

2

f(

α

)

(x

一

α)

2

/

Xl

- 1 \

3 +

(5

,

-1

,

-3)

I

X2

+1 J

飞

X3

I

/ 4 … 1

0

飞/

Xl

-

1

飞

寸仙一

1

，

X2

十

LZ3)i-103ilh+1)

飞

o

3

-2

J

飞

X3

J

3 +

(5Xl

-

X2

-

3X3

…

6)

+ (2xi -

5Xl

-

XIX2

+

X2

十

3X2X3

+

3X3

-

x~

十

3)

2xi

-

x

向

+3x

仇

-zi

f(x)

，

口

Pro

blem

10:

Let

u(x

,

t)

I 2

~-已一古，

for

t

>

0

,

x

ξJR.

飞

/4

时'

Compute

絮

and

g

主，

and

show

that

θuθ2

也

θtθz2·

Note:

This exercise shows

that

the

function

u(

x

,

t)

is

a

solution of

the

heat

equation.

In

fact

,

u(x

,

t) is

the

fundamental solution of

the

heat

equation

,

and

is used

in

the

PDE

deri

飞

ration

of

the

Black-Scholes formula for pricing

European

plain vanilla options.

Also

,

note

that

u(x

,

t)

is

the

same as

the

density function of

a

normal

variable

with

mean

0

and

variance

2t.

Solution: By direct

computation

and

using

the

Product

丑

ule

，

we

find

that

θ

u

1

'J问

1

.r

2

1

.r

2

(

x

2

(

1\\

一一

=

一

_t-u/~

一-=

e

"4

τ+

一一

=

e-

4i

I

一一.

I

一

~II

at

2

V

y4王

d

召

\4\

t

2

)

.r

2

x

2

1

.r

2

=一一一

=e

右十一·一

=e

一石;

(1.

9)

2t

y4巧

4t

2

y4言:

θ

u

x

1

.r

2

一一一

ω

-

-…-叩】

.--…-一

ρ

4t·

ax

2t

v4

1r

t

~

,

24

CHAPTER

1.

CALCULUS

REVIE1

iV.

PLAIN

VANILLA

OPTIONS.

1.1.

SOLUTIONS

TO

CHAPTER

1

EXERCISES

25

θ

2

U

δ

x

2

••

E

,,,,,,

nu

4t4

S(T)

<

30 30

<

S(T)

<

35 35

< S

T)

< 40 40 <

S(T)

黯

mm

。

S(T)

-

30

S(T

-

30

S(T)

-

30

。

S(T

-

35

sjTj35

O

。

SrT)

-

40

O

S(T)

-

30

40 -

S(T)

。

From

(1.

9)

and

(1.

10),

we

c

∞

onc

叫

i

比

tcll

时

e

t

由

ha

创

t

θ

2

U

θu

θ

x

2

θ

t'

L....J

Problem

11:

Co

斗

sider

a portfolio with

the

following positions:

• long one call option with strike K

1

=

30;

• short two call options with strike K

2

=

35;

• long one call option with strike K

3

= 40.

All options are on

the

same

underlyi

吨

asset

and

have

maturity

T. Draw

the

payof

dlagram

at

maturity

of tile portfolio?i.e-7plot

the

value of

the

port

fo

lio V(T)

at

m

at

uyity as a function of S(T)7the price of the m d

e

臼创

rl

J

坊刷

y

抖

rm

S

臼

se

创

t

a

肮

t

time

T.

Note: This is a

but

臼

rgy

pead

A

tMer

mks

a

10

吨

Pωi

阳

1

in a

b

飞阳

rfly

pread

if

the

price of

the

underWIngmset

at

maturity

is expected

to

be

h

the

K

1

三

S(T)

三

K

3

range.

SoJTLtiOTZJA

butterny

spread is

&Il

optiOIls portfolio

made

of

a long positiOII

IIe

call option with strike

kh

a long position

iIla

call option

with

strike

khazld

a

short

position

intwo

calls

with

strike equal

to

the

average

of

tlm

strikes K

1

and

K3 , i.e., with strike

K

2

二且寿县

;

all options have

the

same

maturity

and

have

the

same underlying

asse(

The

payof

at

maturity

of a

butterdy

spread is aiways11OIIIlegativtand

it

is

POSItive

if ttle price of

the

mdeElying asset

at

maturity

is

betweeiltbe

strikes K

1

and

K

3

,i.e., if K

1

<

S(T)

<

K;.

For our particular example?tfle values

of

the

three

call options

at

maturity

e, respectively,

Problem

12:

Draw

the

payoff diagram

at

maturity

of a bull spread

with

a

long position

in

a call

with

strike

30

and

short a call with strike

35

, and of a

bear

spread

with

long a

put

of strike

20

and

short a

put

of strike

15.

Solution:

The

payoff of

the

bull spread

at

maturity

T is

只

(T)

=

max(S(T)

30

,

0)

-

max(S(T)

-

35

,0).

Depe

口

ding

on

the

value of

the

spot price

S(T)

,

the

value of

the

bull spread

at

maturity

Tis

I

S(T)

< 30 I30 <

S(T)

<

35

I

35

<

S(T)

I

vi

(T)

I 0 I

S(T)

30

I 5

The

value of

the

bear

spread

at

maturity

T is

巧

(T)

= max(20 -

S(T)

,

0)

- max(15 -

S(T)

,

0)

,

which can

be

written

i

口

terms

of

the

value of

S(T)

as

C

1

(T)

C

2

(T)

C

3

(T)

max(S(T)

- K

1

,0)

皿

ax(S(T)

- K

2

,0)

max(S(T)

- K

3

,0)

max(S(T)

-

30

,0);

max(S(T)

-

35

,0);

max(S(T)

- 40,

0)

A

trader

takes a long position

in

a bull spread if

the

underlying asset is

expected

to

appreciate in value, and takes a long position

in

a bear spread if

the

value of

the

underlying asset is expected

to

depreciate.

口

V(T)

= C

1

(T)

2C

2

(T)

+C

3

(T).

Problem

13:

Which of

the

following two portfolios would you rather hold:

• Portfolio

1:

Long one call option with strike K = X - 5 and long one call

option with strike

K =

X

十

5;

• Portfolio

2:

Long two call options with strike K =

X?

(All options are on

the

same asset and have

the

same maturity.)

Solution: Note

that

being long Portfolio 1

and

short Portfolio 2 is equivalent

to

bei

吨

long

a

butte

and

the

value of

the

portfolio

at

maturity

is

Depend,ing o,n

t~~

，

~~lu~s_

of

the

spot

S(T)

of

the

underlying asset

at

maturity

,

the

value

V(T)

of

the

portfolio

at

t'i~e

T is given

beiow~

27

SOLUTIONS

TO

CHAPTER

1 EXERCISES

VeT)

当〈几

O

K

1

< SeT) < K

2

3Z22S

1δS

TiT-

一

-Z

Z1K1

K

2

<

S(T

页

)

<

K

3

(Xl

+

x2)S(T)

-

X1K1

X2K2

K

3

<

SeT)

(Xl

十

X2

+

x3)S(T)

-

x

1

K

1

-

X2

K

2

-

X3K3

1.1.

Note

that

VeT)

is

no

日

negative

whe

丑

SeT)

三

K

2

only

if a long position is

taken

in

the

option

with

strike K

1

,

i.e.

,

if

Xl

三

0.

The

payoff

VeT)

decreases

when

K

2

<

SeT)

<

K

3

,

accounting for

the

short

position

in

the

two

call

options

with

strike K

2

,

and

then

increases when

SeT)

三

K

3

·

We

conclude

that

VeT)

三°

for

any

value of

SeT)

if

and

∞

ly

if

Xl

主

0

，

if

the

value of

the

portfolio when S

(T)

=

K

3

is

nonnegative

,

i.e.

,

if

(Xl

十

x2)K

3

-

X1

K

1

-

X2

K

2

~三

0

，

and

if

Xl

十

b

十均主

0.

Thus

,

an

arbitrage

exists

if

and

only

if

the

values

C

1

(0)

,

C

2

(0)

,

C

3

(0)

are

such

that

we

can

find

Xl

,

X2

,

and

X3

with

the

following properties:

。;

0;

0.

For C

1

(0)

=

8

,

C

2

(0)

=

5

,

C

3

(0)

=

3

and

K

1

=

100

,

K

2

=

120

,

K

3

=

130

,

the

problem

becomes finding

Xl

主

0

，

and

X2

and

X3

such

that

(For these

option

prices

,

arbitrage

will be possible

since

the

middle

option

is

overpriced

relative

to

the

other

two options.)

The

easiest way

to

find values

of

Xl

,

X2

,

and

X3

satisfying

the

constraints

above is

to

note

that

arbitrage

can

occur

for

a portfolio

with

long positions in

the

options

with

lowest

and

highest

strikes

,

and

with

a

short

positio

日出

the

option

with

middle strike

(note

the

similarity

to

butterfly

spreads).

Then

,

choosi

吨

X3

=

-Xl

-

X2

would

be

optimal;

ef.

(1.

13).

The

constraints

(1.

11)

and

(1.

12) become

(1.

11)

(1.

12)

(1.

13)

。;

0;

0.

8X1

+

5X2

+

3X3

30X1

+

10x2

Xl

十

X2

+

X3

- 1

and

X2

-

-3

,

which

nunu

These

constraints

are

satisfied

,

e.g.

,

for

Xl

corresponds

to

X3

=

2.

Xl

C

1

(0)

+

X2C2(0)

十

X3

C

3(0)

Xl

(Xl

十

x2)K

3

-

X1

K

1

-

X2

K

2

Xl

+

X2

十

X3

<

>

5X1

+

2X2

3X1

+

X2

CALCULUS

REVIE1

iV.

PLAIN

VANILLA

OPTIONS.

rather

aomegative)payof

M

maturity-Ttmrefore7if

you

are

to

α

ss

包

ω

un

η

阳

7

POSItion

ln

either

om

of

th

portfolios

(口

ot

to

purchase

the

portfolios)

,

you

are

better

of

owniIlg

Portfolio

17since

its

payofat

maturity

wiH

always

be

at

least as

big

as

the

payoff

of

Portfolio

2.

More

precisely

,

note

that

CHAPTER

1.

26

问

(T)

-

\i2

(T)

max(S(T)

一

(X

-

5)

，

0)

十

max(S(T)

一

(X

+

5)

,

0)

-

2max(S(T)

-

X

,

O).

V(T)

The

value

of

the

portfolio

at

time

T

is

detailed

below:

V(T)

S(Tf<X

-

5

O

X

-

5

<

S(T)

<

X

S(T)

一{~-

5)

X

<

S(T)

<

X

+

5

(X

+

5)

--

S(T

X_+

5

<

S(T)

。

Problem

14:

Call

options

with

strikes

100

,

120

,

an

丑

d

130

on

the

sam

丑

le

under-

l

牛

yi

凶

n

吨

g

ass

们

E

时

w

呐

it

由

ht

出

h

盯

e

sa

缸

me

丑

lema

肮刷

t

机切

u

江哟

I

(there

is no

bid-ask

spread).

Is

there

an

arbitrage

opportunity

prese

时?

If

yes

,

how

can

you

make

a

riskless

pro

缸?

SoJTLUOTZJFor

marbitrage

opPOEtunity

to

be

preseIlt7there

must

be

a

portm

folio

made

of

the

three

options

with

nonnegative

payoff

at

maturity

and

with

a negative

cost

of

setting

up.

Let

K

1

=

100

<

K

2

=

120

<

K

3

=

130

be

the

strikes

of

the

options.

Denote

,

by

x~

，

X2

,

!3

..!~e

options

positions

(which

can

be

either

negative

or

positive)

at

time

0.

Then

,

at

time

0

,

the

portfolio

is

worth

十

X3

C

3(0)

十

X2

C

2(0)

=

X1

C

1(0)

V(O)

At

maturity

T

,

the

value

of

the

portfolio

will

be

X1

C

1(T)

+

X2

C

2(T)

十

X3

C

3(T)

Xl

max(S(T)

-

K

1

,

0)

+

X2

max(S(T)

-

K

2

,

0)

+

X3

四

ax(S(T)

-

K

3

,

0)

,

V(T)

respectively.

Dependi

鸣

on

the

value

S(T)

of

the

underl}

也

g

asset

at

maturity

,

the

value

V(T)

of

the

portfolio

is

as follows:

28

CHAPTER

1.

CALCULUS

REVIEW.

PLAIN

VANILLA

OPTIONS.

V(O)

=

一

P(O)

-

S(O)e-

qT

十

C(O)

+ 39.5821 =

O.

Note

that

by shorting

the

shares

you

are

responsible for paying

the

accrued

dividends. Assume

that

the

dividend

p

句

rments

are

financed

by

shorting

29

more shares of

the

underlying asset

and

usi

吨

the

casg

proceeds

to

make

the

dividend payments.

Then

,

the

short

position

in

e-

q1

shares

at

time

0 will

become a

short

position

in

one

share

1

at

time

T.

The

value

of

the

portfolio

at

maturity

is

V(T)

= -

P(T)

-

S(T)

+

C(T)

+39.5821e

rT

.

Recall from

the

proof

of

the

Put-Call

parity

that

P(T)

+

S(T)

-

C(T)

=

max(K

-

S(T)

,

0)

+

S(T)

-

max(S(T)

- K ,

0)

= K ,

regardless of

the

value

S(T)

of

the

underlying asset

at

maturity.

Therefore,

V(T)

=

一

(P(T)

十

S(T)

-

C(T))

+39.5821e

rT

- - K + 39.5821e

rT

- - 40 + 40.2473 - 0.2473.

This

value represents

the

risk-free profit

made

by

exploiting

the

discrep-

ancy from

the

Put-Call

parity

,

and

is

the

same

as

the

future

value

at

time

T

of

the

misprici

吨

from

the

Put-Call

parity;

d.

(1.

15).

口

Problem

16:

The

bid

and

ask prices for a six

months

European

call option

with

strike 40

on

a

non-dividend-paying

stock

with

spot

price

42

are

$5

and

$5.5, respectively.

The

bid

and

ask prices for a six

months

European

put

option

with

strike 40

on

the

same

underlying asset are $2.75

and

$3.25,

respectively. Assume

that

the

risk free

rate

is equal

to

O.

Is

there

an

arbitrage

opportunity

present?

Solution: For r = 0,

the

Put-Call

parity

becomes P +S - C = K , which in

this

case

can

be

written

as C - P =

2.

Thus

,

an

arbitrage

occurs if C - P

can

be

"bought"

for less

than

$2

(i.

e.

,

if a call

option

is

bought

and

a

put

option

is sold for less

than

$2),

or

if C - P

can

be

"sold" for more

than

$2

(i.e., if a call

option

can

be

sold

and

a

put

option

can

be

bought

for more

than

$2).

From

the

bid

and

ask

prices,

we

直

nd

that

the

call

can

be

bought

for $5.5

and

the

put

can

be

sold for $2.75.

Then

, C - P

can

be

"bought" for

$5.ι

$2.75=$2.75, which is more

than

$2. Therefore, no risk-free profit

can

be

achieved

this

way.

Also

, a call

can

be

sold for

$5

and

a

put

can

be

bought

for $3.25. There-

fore

, C - P

can

be

"sold" for $5-$3.25=$

1.

75, which is less

than

$2. Again,

no risk-free profit

can

be

achieved.

口

lThis

is

similar

to

converting

a

long

pm;ition

in

c

qT

shares

at

time

0

into

a

long

position

i

丑

one

share

at

time

T:

thro

吨

h

continωus

purchases

of

(fractions

of)

shares

usi

吨

the

dividend

payments:

which

is

a

more

intuitive

process.

1.1.

SOLUTIONS

TO

CHAPTER

1

EXERCISES

(1.

15)

(39.5821

-

39.3389)

产=

0.2473

Buying

one

option

with

strike 100, selling

three

options

with

strike 120,

and

buying

two options

with

strike 130 will

generate

a positive cash flow of

$1

,

and

will result in a portfolio

that

will

not

lose money, regardless

of

the

value of

the

underlying asset

at

the

maturity

of

the

options.

口

since

shorting

the

shares means

that

e-

qT

shares

are

borrowed

and

sold

on

the

market

for cash.

(The

short

will

be

closed

at

maturity

T

by

b

可

i

吨

shares

a

丑

the

market

and

returning

them

to

the

borrower; see below for

more

details.)

At

time

0,

the

portfolio consists of

the

following positions:

•

short

one

put

option

with

strike K

and

maturity

T;

•

short

e-

qT

shares;

• long one call

option

with

strike K

and

maturity

T;

• cash: +$39.582

1.

The

initial value of

the

portfolio is zero, since no money were invested:

To show

this

,

start

with

no money

and

sell one

put

option

,

short

e-

qT

shares,

and

buy

one call option.

This

will

generate

the

following

cash

amount:

P +

Se-

qT

- C 39.5821,

Problem

15:

A

stock

with

spot

price 40 pays dividends continuously

at

a

rate

of

3%.

The

four

months

at-the-money

put

and

call options

on

this

asset

are

trading

at

$2

and

$4, respectively.

The

risk-free

rate

is

constant

and

equal

to

5%

for all times. Show

that

the

Put-Call

parity

is

丑

at

satis

丑

ed

and

explain how would you

take

advantage

of

this

arbitrage

opportunity.

Solution:

The

followi

吨

values

are

give

口

:

S = 40; K = 40; T =

1/3;

r = 0.05;

q = 0.03; P =

2;

C =

4.

The

Put-Call

parity

is

not

satisfied, since

P +

Se-

qT

- C - 39.5821 > 39.3389 -

Ke-

rT

.

(1.

14)

Therefore, a riskless profit

can

be

obtained

by "buying low

and

selling

且

igh

飞

i.e.

，

by

selling

the

portfolio

a

丑

the

left

hand

side of (1.14)

and

buying

the

portfolio

on

the

right

hand

side of (1.14) (which is

cash

only).

The

riskless

profit

at

maturity

will

be

the

future

value

at

time

T of

the

mispricing from

the

Put-Call

parity

, i.e.,

At

maturity

,

the

asset is bought for 12100 and

the

short is closed (the

dividends paid on

the

short position increase

the

size of

the

short position

to

1 unit of

the

index).

The

realized gain is

the

interest accrued

on

the

cash

resulting from

the

short position minus 12100, i.e.,

e

O

.

08

/

4

(e-

O

.

03

30

CHAPTER

1.

CALCULUS

REVIEVV.

PLAIN

VANILLA

OPTIONS.

Problem

17:

You expect

that

an

asset

with

spot price

$35

will

trade

in

the

$40

一

$45

range in one year. One year

at-the-money

calls on

the

asset

can

be

bought for

$4.

To act on

the

expected stock price appreciation, you

decide

to

either

buy

the

asset,or

to

buy

ATM calls. Which

strategy

is

better

,

depending

on

where

the

asset price will

be

in a year?

Solution: For every $1000 invested,

the

payoff

i

口

one

year of

the

first

strategy

,

i.e.,of buying

the

asset, is

叫

T)

=

1~~0

S(T)

,

w

且

ere

S(T)

is

the

spot price of

the

asset

in

one year.

For every $1000 invested

,

the

payoff

in

one year of

the

second strategy,

i.e.,of investing everything in buying call options,is

1I2

(T)

=

半

max(S(T)

-

35

，

0)

工(平叫

)-35)iijzjZZJ

It

is easy

to

see

that

,if

S(T)

is less

than

$35,

than

the

calls expire worth-

less

and

the

speculative strategy of investing everything in call options will

lose all

the

money invested in it, while

the

first

strategy

of buying

the

asset

will

not

lose all its value. However, investing everything in

the

call options

is very

pro

自

table

if

the

asset appreciates

in

value, i.e. ,is

S(T)

is

signi

五

cantly

larger

than

$35.

The

breakeven point of

the

two strategies,i.e.,

the

spot price

at

maturity

of

the

underlying asset where

both

strategies have

the

same payoff

is $39.5161

, since

1000

_._, 1000

一:~

S(T)

=

一一

(S(T)

-

35)

仁斗

S(T)

= 39.516

1.

35

If

the

price of

the

asset will,indeed,

be

i

口

the $40

一

$45

range in one year,

then

buying

the

call options is

the

more profitable

strategy.

口

Problem

18:

The

risk free

rate

is

8%

compounded continuously

and

the

dividend yield of a stock index is 3%.

The

index is

at

12

,000

and

the

futures

price of a contract deliverable in three months is

12

,100. Is there

an

arbitrage

opportunity

, and how do you take advantage of it?

Solution:

The

arbitrag

e-

free futures price of

the

futures contract is

12000e

r

-

q

)T

=

12000e(0.08

一

0.03)/4

12150.94 > 12100.

Therefore

,

the

futures contract is underpriced

and

should

be

bought while

hedged statically by shorting

e-

qT

= 0.9925 units of index for each futures

contract

that

is sold.

1.1.

SOLUTIONS

TO

CHAPTER

1

EXERCISES

31

32

CHAPTER

1.

CALCULUS

REVIEW.

PLAIN

VANILLA

OPTIONS.

1.2

Supplemental

Exercises

1.

Compute

户口

(x)

dx

2.

Compute

J

xne

x

dx

3.

Compute

J

(I

n(

x)

)n

dx

4.

Show

that

>-

Z

]

V

+

z

\11I/

1-z

/IIlt\

<

e

<

Z

l-z

+

/it\

5.

Let

(

(x

一

μ)2\

f(x)

=

一古

=exp(-

i

σ

〉习作

\

2σ2

)

Assume

that

g :

JR

•

JR

is a continuous function which is uniformly

bounded

, i.e.,

there

exists a

constant

C such

that

jg(

x)

I

三

C

for all

x E

JR.

Then

, show

that

M:

削川

x

=

g(

μ)

6.

Let

内)工艺

Ci

Compute

g'

(y).

7.

A derivative security pays a cash

amount

C if

the

spot

price of

the

underlying asset

at

maturity

is between K

1

and

K

2

,where 0 < K

1

< K

2

,

and

expires worthless otherwise. How do you synthesize

this

derivative

security (i.e.

,how do you recreate

its

payoff almost exactly) using plain

vanilla call options?

1.

3.

SOLUTIONS

TO

SUPPLENIENTAL

EXERCISES

33

8.

Create

a portfolio

with

the

following payoff

at

time

T:

(

2S(T)

, if

0

三

S(T)

<

20;

V(T)

= <

60

-

S(T)

, if

20

三

S(T)

<

40;

l

S(T)

-

20

, if

40

三

S(T)

，

where

S(T)

is

the

spot

price

at

time T of a given asset. Use plain

vanilla options

with

maturity

T as well as cash positions

and

positions

in

the

asset itsel

f.

Assume, for simplicity,

that

the

asset does not pay

dividends

and

that

interest

rates

are zero.

9.

Call options

on

the

same underlying asset

and

with

the

same

maturity

,

with

strikes K

1

< K

2

< K

3

, are

trading

for C

1

, C

2

and

C

3

,respectively

(no

Bid-Ask

spread),

with

C

1

> C

2

> C

3

.

Find

necessary

and

sufficie

时

conditions

on

the

prices C

1

, C

2

and

C

3

such

that

no-arbitrage

exists

corresponding

to

a portfolio

made

of positions in

the

three

options.

10. Denote by C

bid

and

C，

α

sk

，

and

by

1

毛

id

and

~α

sk

，

respectively,

the

bid

and

ask prices for a plain vanilla

European

call

and

for a plain vanilla

European

put

option,

both

with

the

same strike K

and

maturity

T ,

and

0

日出

e

same underlying asset

with

spot

price S

and

paying dividends

continuously

at

rate

q.

Assume

that

the

risk-free interest

rates

are con-

stant

equal

to

r.

Find

necessary

and

sufficient

no-arbitrage

conditions

for

Cbid

,

Cask

,

Pbid

,

and

凡

sk·

1.3

Solutions

to

Supplemental

Exercises

Problem

1:

Compute

Jx

n

ln(x)

dx

Solution:

If

n

乒

-1

，

we

use integration by

parts

and

find

that

fzn+llf

x

n

ln(x)

dx

=

一

-Mz)-j

zn+1·-dz

η+1η

十

1)

x

n

十

11

n

(

吟

x

n

十

1

、

A

+

C.

For n

=

一

1

，

we

obtain

that

rn~x)

一

WJ

dx

=

(ln(x)?

+

C.

口

Stefanica D. Solutions Manual: A Primer For The Mathematics Of Financial Engineering

Подождите немного. Документ загружается.