Stefanica D. Solutions Manual: A Primer For The Mathematics Of Financial Engineering
Подождите немного. Документ загружается.


155
SOLUTIONS
TO
SUPPLEMENTAL
EXERCISES
6.3.
FINITE
DIFFERENCES.
BLACK-SCHOLES
PDE.
CHAPTER
6.
(ii) For q = 0,
we
obtain
from (6.34)
and
(6.35)
that
-
rKe-
rT
N(d
2
).
σ
8V2
7r
T
σ8
_~
二百万
e
2
154
connecting
the
f
and
the
8 of plain vanilla
European
options is exact if
the
underlying asset pays no dividends a
r:
d if
the
risk-free interest
rates
are zero.
In
oth~r
';ords
,for, e.g.,call options
!,
f(C)
8(C)
AU
σ28
2
f(C)
1
十一-一·一一
2
8(C)
+γ
Ke-
rT
N(d
2
)
σSfii
2
V2irT
V -
σ
S
~一手
2
V2irT
V -
rK
e-
rT
N(d
2
)
uS
p.
一手
2
飞!27r
T-
+γ
Ke-
rT
N(d
2
)
1
一
σ28
2
f(C)
1+
一一一·一一一
2
8(C)
Then
,
1
l+~u
rn:;旦旦~.
2rVT
N(d
2
)
(ii)
If
q = 0
and
r
笋
0
,
show
that
1
十
σ28
2
f(C)
一---.一
2
8(C)
(iii) Consider a
si
议
xmo
∞
n
川
thsp
抖
la
创
i
川
a
缸
ωani
丑川
l
让
i
让
llaE
盯
opea
缸
I
川
allopμtio
∞
I
丑
ω1
on
an
unde
臼创
rlyi
沁
I
口
l
asset
with
s
印
po
创
t
price 50
and
volatility 30%. Assume
that
the
interest
rates
are constant
at
4%.
If
the
asset pays no dividends, compute
1
1+
~
U
1m
S .
l.-
e
一手
rVT
Ke-
rT
N(d
2
)'
J2王
1
σ28
2
f(C)
1
十一一一·一一一
2
8(C)
(6.36)
since
N'(t)
=
在
λfor
all
tεR
Recall
that
the
"magic" of Greek computations is due
to
the
following
result:
1+
动
T
K:JX:Zii2)
if
the
options are
at-the-money
, 10%, 20%, 30%,
and
50%
in-th
e-
money,
and
10%, 20%, 30%,
and
50%
out-of-th
e-
money, respectively.
What
happens
if
the
asset pays dividends continuously
at
a 3% rate?
1
l+~ulm
旦旦~.
rVT
N(d
2
)
8
N'(d
1
) =
Ke-
rT
N'(d
2
);
cf.
Lemma 3.15 of
[2]
for q =
O.
Then
, (6.36) becomes
σ28
2
f(C)
1
十一一一·一一
2
8(C)
Solution: Recall
that
the
f
and
the
8 of a plain vanilla
European
option are
(6.34)
e-qT-fi
aS
V2
汗
7
σ
8e-
qT
_5.
2V2
7r
T
e
2
c
pi
(6.35)
- r K e
-rT
N
(d
2
)
,
十
qSe
一叫
V(d
1
)
8(C)
(iii) Let 8 = 50 , T =
0.5
,
σ=
0.3,
and
r = 0.04.
The
table
below records
the
values of
σ28
2
f(C)
l
十一-一·一一一
2
8(C)
(denoted by
"Val
时')
both
for q = 0,
and
for q = 0.03, for
the
following
values of
the
moneyness of
the
option:
S
K
where d
1
=
(In
(圣)十(叫到
T)
/
(σvr)a
叫
=
d
1
一
σ
♂
(i) For r = q = 0,
we
obtain
from (6.34)
and
(6.35)
that
σS-fi
2V2
7r
T
8(C)
σS
刁万
e2;
f(C)
{1,
1.
1,
1.
2,
1.
3,
1.
5,0.9,0.8,0.7,0.5},
corresponding
to
call options
that
are
at-th
e-
money, 10%, 20%, 30%,
and
50%
in-the-money
,
and
10%,20%,30%,
and
50%
out-of-the-money
,respec-
tively:
=
O.
Then
,
1+σ2S2r(C)-1+σ2~2
(_~飞
十一.---一
十二
,
2θ
(C)
2\σ28
2
)
lNote
that~
if r = q =
O~
then
f(
P)
=
f(
C) and
8(P)
=
8(C).

156
CHAPTER
6.
FINITE
DIFFERENCES.
BLACK-SCHOLES
PDE.
6.3.
SOLUTIONS
TO
SUPPLEMENTAL
EXERCISES
157
-S
IK
Value for q = 0
Value for q = 0.03
1 0.1897
0.0238
1.
1
0.2582
0.0233
1.
2
0.3518
0.0144
1.
3
0
.4
711
-0.0187
1.
5
0.7361
-0.5503
0.9
0.1412
0.0214
0.8
0.1068
0.0184
0.7
0.0822
0.0155
0.5
0.0505
0.0107
We
note
that
the
approximation
σ
2S2
r
1+
一一一·一但
O
2 e
is
better
for deep
out-of-the-money
options (corresponding
to
small values
of
SI
K)
and
is worse for deep
in-th
e-
money options (corresponding
to
large
values of
SI
K).
Also, for this particular case,
the
approximation is more
accurate if
the
underlying asset pays
dividends.
口
Problem
4: Consider a six months 5%
in-th
e-
money plain vanilla European
call option
with
strike 30 on
an
underlying asset
with
spot
price 20
and
volatility 20%,paying dividends continuously
at
a 2% rate. Assume
that
the
interest rates are constant
at
5%.
(i) Use central differences
to
corr
职
lte
the
finite difference approximations
~e
and
f e for
~
and
f , respectively,i.e.,
Solution:
The
spot price S = 3
1.
5 corresponds
to
a 5% ITM call
with
K = 30.
We
find
that
~
= 0.692130579727
and
r = 0.077379043990.
The
central
且
nite
difference approximations
~e
and
the
approximation
errors I
~e
-
~
I are recorded
in
the
table below:
dS
~e
I~e-~I
0.1
0.692112731743
0.000017847983
0.01
0.692131730564
0.000001150838
0.001
0.692131920566
0.000001340839
0.0001
0.692131922513
0.000001342786
10-
b
0.692131922087
0.000001342360
10-
0
0.692131918000
0.000001338274
10-(
0.692131916226
0.000001336498
10-δ
0.692131862934
0.000001283207
10-
\:1
0.692132573477
0.000001993750
10-
1υ
0.692104151767
0.000026427960
10-
11
0.691890988946
0.000239590780
10-
U
0.687450096848 0.004680482879
The
approximations became more precise when
dS
decreased,until
dS
=
10-
8
;
the
best approximation was within
about
10-
6
of~.
However,for values
of
dS
smaller
than
10-
9
,
the
finite difference approximations deteriorated very
quickly.
To explain this phenomenon
, denote
the
exact value
2
of Delta by
~exaet.
Note
that
the
value of
~
is
given
by
the
Black-Scholes formula, i.
e.
,
~
=
~BS
=
e-
qT
N(d
1
).
f
e
~e
This value is computed using a numerical approximation of
N(d
1
)
that
is
accurate within
7.5 .
10-
7
;
d.
[1
],
page 932.
In
other
words,
we
0
日
ly
know
that
When
computing
the
且
nite
difference approximation
~e
,
we
use a nu-
merical estimation of
the
Black-Scholes formula
to
compute
C(S
+
dS)
and
C
(S
-
dS)
which once again involves
the
numerical approximation of
the
cumulative density of
the
standard
normal variable. In other words,
(6.38)
(6.37)
I~BS
-
~exaetl
<
10-
6
.
~e
=
CBS(S
十
dS)
-
CBS(S
- dS)
-
2dS
2N
ate
that
~exact
is
a
theoretical
value
,
and
is
口
at
the
~
from
the
table
above.
C(S
+
dS)
…
C(S
-
dS)
2dS
'
C(S
+
dS)
-
2C(S)
十
C(S
-
dS)
(dS)2
for
dS
=
10-
2
with i = 1 :
12
,where,e.g.,
C(S
十
dS)
=
C(S
+
dS
,K ,
T
,
σ
,
r)
denotes
the
Black-Scholes value of
the
call option corresponding
to
a spot
price
S +
dS
of
the
underlying asset.
(ii) Compute
the
Delta
and
Gamma
of
the
call using
the
Black-Scholes for-
mula
,
and
the
approximation errors
I~e
-
~I
and
Ife q. Note
that
these
approximation errors stop improving
, or even worsen, as
dS
becomes
too
smal
l.丑
ow
do you explain this?

158
CHAPTER
6.
FINITE DIFFERENCES. BLACK-SCHOLES PDE.
6.3.
SOLUTIONS
TO
SUPPLE
1V
IENTAL EXERCISES
159
s
dB
•
O.
Since
CBS(S)=SfqTN(dl)-ke--TTlV(d2)7and
since lV(do and
lV(d2)
are
comput~d
'm~merically
within
10-
6
of their exact value,it follows
that
Deω
te
by
Cexaet(B
十
dS) and
C
口
mα
et(B
一
dB)
the
exact
v
刊叫
a
址
lues
of
the
opμt
挝
io
丑
Since
the
central
fi
缸
n
川
l
让
it
臼
ed
出
i
宦
erence
is a
sec
∞
or
丑
ld
order
approx
对
im
丑
1a
创
tion
凡
1
,
i
让
t
follows
that
,for
ex
α
ct
values of Delta and of
the
call options,
~ex
ω=
Cexact(B
+
dB)
-
C
口
aet(B
-
dB)
十
o
((dB)2) ,
2dB
(6.39)
dB
r
e
We
-
f/
0.1
0.077370009586 0.000009034404
0.01 0.077371495486
0.000007548504
0.001 0.077371502982
0.000007541008
0.0001 0.077371709040
0.000007334951
10-
b
0.077271522514 0.000107521476
10-
0
0.074606987255 0.002772056735
10-(
-0.355271367880 0
.4
32650411870
10-
1:>
7
1.
054273576010 70.976894532020
\CBs(B
十
dB)
-
Cexaet(S
十
dB)1
<
α10-j;
jCBs(B -
dB)
-
Cexaet(B
- dB)j
<
α10-°
,
where
αis
a constant proportional to
the
values of
Band
K ,
Usi
吨
(6.38)
and(6.39)
we
find
that
~e
-
~BS
(~e
-
~exaet)
+
(~exaet
-
~BS)
CBs(B +
dB)
-
Cexaet(S
十
dB)
2dB
CBs(B -
dB)
-
C
口创
t(B
-
dB)
2dB
十
~exaet
-
~BS
十 o
((dB?) ,
(6
.4
0)
(6
.4
1)
(6
.4
2)
For
dB
三
10-
9
,
the
values of re increased dramatically, reaching
10
9
for
dB
=
10-
12
, and were no longer recorded.
The
finite difference approxima-
tions of
r became more precise while
dB
decreased
to
10-
4
,
but
were much
worse after
that;
the
best approximation was within
10-
5
of r.
The
reason
for this
is
similar
to
the
one explained above for
the
finite difference approx-
imations of
~.口
as
dB
•
O.
The
only estimate
we
can find using (6.37), (6.40),
(6
.4
1)
, and
(6
.4
2)
for
the
approximation of
~BS
by
~e
as
dB
• o
is
\~e
-
~BS\
三
\CBS(S
十
dB)
-
C
ex
α
et(S
十
dB)1
2dS
十
ICBS(B
-
dB)
-
Cexaet(B
-
dB)j
2dB
+I~exαet
-
~BSj
+ 0 ((dB)2)
α10-
6
〈一一
+
10-
6
+ 0 ((dB)2) ,
dB
(6
.4
3)
as
dB
•
O.
While
the
approximation error
j~e
-
~j
may
be
better
in practice,
the
bound
(6.43) provides
the
intuition behind
the
fact
that
,for
dS
too small,
t_h~
numerical approximation error
I~e
-
~I
=
I~e
-
~Bsl
deteriorates
as
斗主
becomes large.
The central finite difference approximations
re and
the
approximation
errors
Ire
- r j are recorded in
the
table below:

r
e
4L
p
a
c
Multivariable
calculus:
chain
rule
,
integration
by
sUbstitution
,
extremum
points.
Barrier
options.
Optimality
of
early
exercise.
7.1
Solutions
to
Chapter
7
Exercises
Problem
1: For q = 0,
the
formula for
the
Gamma of a plain vanilla Euro-
pean call option reduces to
r
=s
中叫一叮?〉
(7.1)
where
In
(丢)十
(γ
十号
)T
d
1
(S)
=
识
I
(7.2)
飞
IT
Show
that
, as a function of S > 0,
the
Gamma
of
the
call option is first
increasing until
it
reaches a maximum point and
then
decreases. Also, show
that
31lr(S)=O
and
liIII
Y(
句=
°
S
→∞
(7.3)
Sol
仰
on:
From
(7.1)
we
自时
that
r can
be
written as
/
(d
1
(S)? \
r(s)
=
一古二
exp
(一
ln(S)
) , (7.4)
飞
2
---\'-
/ J
where d
1
(S)
is
given by (7.2).
Since
r(S) > 0,
it
follows
that
the
functions r(S) and
ln(r(S))
have
the
same monotonicity intervals. Let 1:
(0
,∞)→1R
given by
1(S)
=
ln(r(S))
=一叩
2
-ln(S)
-1
巾而)

162
CHAPTER
7.
MULTIVARIABLE
CALCULUS.
Then
,
1'
(S)
-~
(1+
扭)
d
1
(S)
1
Sσn
S
(7.5)
Recall from (7.2)
that
d
1
(S)
It
is easy
to
see
that
d
1
(S)
is
an increasing function of S
and
that
gsdl(S)=
一∞;
lim
州)=∞
S
→∞
(7.6)
From (7.5)
we
find
that
I(S)
has one critical
poi
风
denoted
by
S*
, with
d
1
(S*)
=
一
σn.
From (7.5) and (7.6)
it
follows
that
1'(S)
> 0 if 0 < S <
S*
and
1'
(S)
< 0 if
S*
<
S.
In other words,
the
function
I(S)
=
ln(r(S))
is
increasi
吨
when
0 < S <
S*
and is decreasing when
S*
<
S.
We
conclude
that
r(
侈
S)
川
is
a
址
Isωo
1
沁丑肌
C
盯
reaωasl
且
i
恒
I
丑
1
when 0 < S <
S*
and decreasing when
S*
<
S.
We
now compute
lir
町、
o
r(S)
and
lims
→∞
r(s).
Note
that
lims
→∞
d
1
(S)
=
∞.
Therefore,
1 (
(d
1
(S))2
\
Fm
r(S)
=
lim
一?古
exp
(一
-ln(S)
I =
O.
S
→。
G
"
S
→∞
σV
'l.作
l\2
\
I)
Fro
皿
(7.2)
,
and using
the
fact
that
lims
\o
ln(S)
=一∞,
it
follows
that
s
n-WM/
2-n
Ju
…-
mwa
1:
…
{(ln(S)
-
1
日
(K)
+
(γ+
~2)
T)
2I
1 )
s~o
\
2σ2T(1
日
(S))2
'
1
口
(S)
J
2σ
2T
Since
Ii
町、。
(exp
(一
(ln(S)?))
= 0,
we
obtain
that
/一
(d
1
(S)?
\
(门一
ln(S)
I = 0
S\O\
乙/
7.1.
SOLUTIONS
TO
CHAPTER
7
EXERCISES
163
from
(7
.4),
we
conclude
that
1 (
(d
1
(S))2
\
li~
r(S)
-
li~
一万亏
exp
(一
门
-ln(S))
=
O.
口
3
、
v
a
、
uσV
L:
7r
1 \
中/
Problem
2: Let D be
the
domain bounded by the x-axis, the y-axis, and
the
line
x
十
ν=
1.
Compute
fLEjdzdu
(7.7)
Solution: Note
that
D = {(x,y) I
x
主
O
,
y
三
O
,
X
十
y
三
1}
We
use
the
change of variables 8 = X
十
y
and t = x - y,which
is
equivalent
to
S
十
t
8 - t
x -
-2-;
y -
-2-
It
is
easy
to
see
that
(x
,
y)
ε
D
if and only if
(8
,
t)
εn
,
where
n = {(8,t) I
0
三
S
三
1
,
-8
三
t
三
8
}.
The Jacobian of
the
change of variable
(x
,
y)
εD
→
(8
,
t) E n is
lθzθuδzθyl
dxdy =
I
一一一一
~V
I d8dt -
~d8dt
,
lθsθtθtθ81
and therefore
f
儿
:jM=f(/:
二战
)
ds
ij1:(l:tdt)ds=0
j
儿可叫
fL7fjdzdu
l'
U'-Y~
号刊
dy
L
((x
-
2yln(
川))
I~
二
tu
句)
l'
1-
y
+
勾
ln(y)
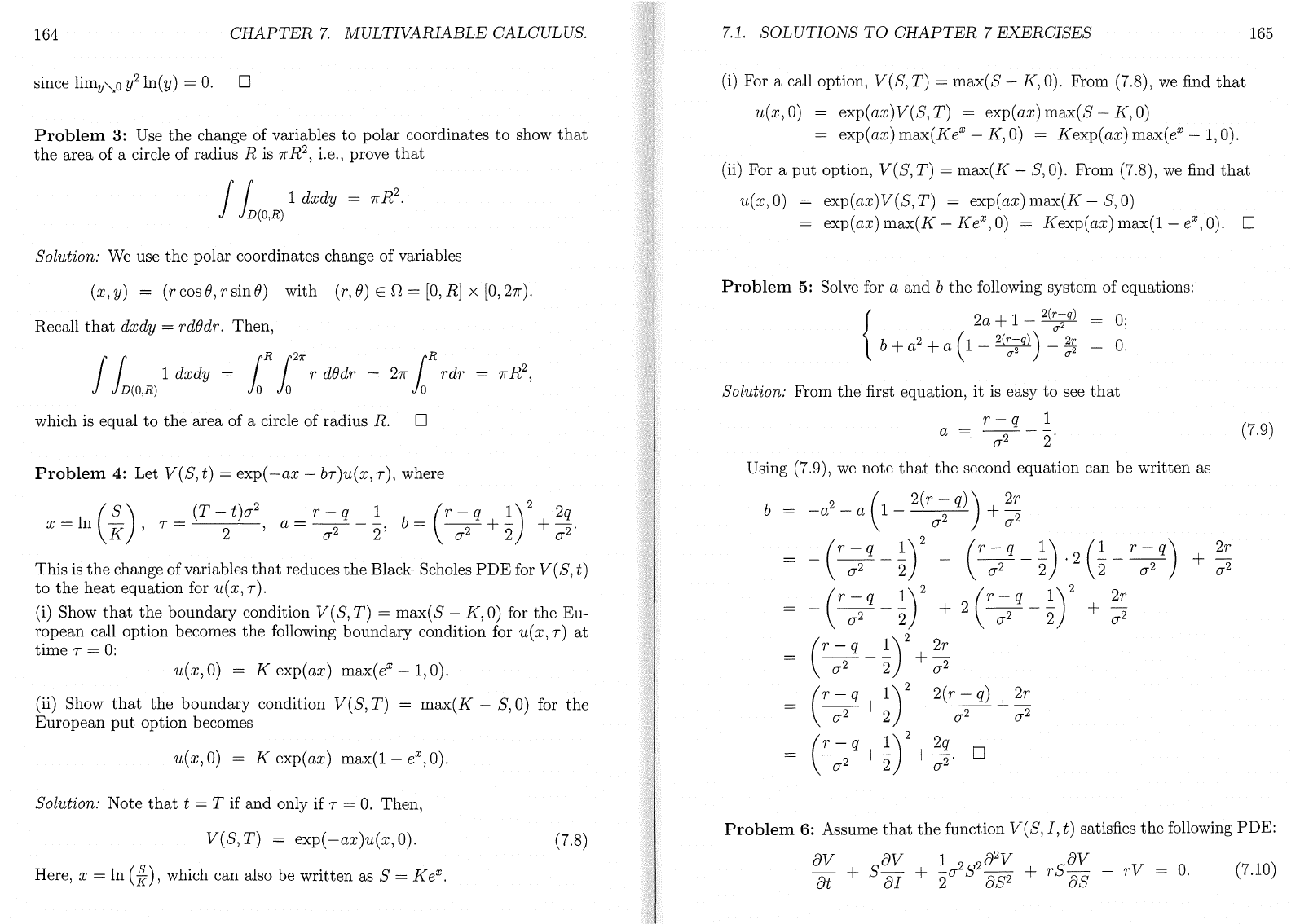
u(x
,
O)
= K
exp(α
x)
max(l
-
eX
,
0).
Solution: We use
the
polar coordinates change of variables
si
丑
ce
limy\o y
2
I
n
(y)
=
O.
口
165
(7.9)
Solution: From
the
且
rst
equation,
it
is easy
to
see
that
Usi
吨
(7.9)
,
we
note
that
the
second equation can be
written
创
b =
~a2
- a
(1
一勺牛二
一(子
-D
2
一(子
-D'2G
一子
)+Z
(子
~r
十
2(
子
-D
2
十二
(子
-32+
主
(子
+;)2-2(γ)
十三
(子寸
)24
口
Problem
5: Solve for
αand
b
the
following system of equations:
(
川一半-
0;
b+
ια(1-~)
~去
z
。
(i) For a call option,
V(S
,
T)
=
max(S
- K ,
O).
From
(7.8)
,
we
find
that
u(x
,
O)
=
exp(α
x)V(S
,
T)
=
exp(α
x)
max(S
- K,
O)
-
exp(α
x)
max(Ke
X
- K
,
O)
-
Kexp(
α
x)
max(e
X
一
1
,
0).
(ii) For a
put
option,
V(S
,
T)
=
max(K
- S,
O).
From
(7.8)
,
we
且时
that
u(x
,
O)
工
exp(α
x)V(S
,
T)
=
exp(α
x)
max(K
- S,
O)
-
exp(α
x)max(K
-
KeX
,
O)
-
Kexp(
α
x)
max(1 -
eX
,
0).
口
7.
1.
SOLUTIONS TO
CHAPTER
7 EXERCISES
CHAPTER
7.
MULTIVARIABLE CALCULUS.
This is
the
change ofvariables
that
reduces
the
Black-Scholes
PDE
for
V(S
,t)
to
the
heat
equation for u(x,
T).
(i) Show
that
the
boundary condition
V(S
,
T)
=
max(S
- K ,
O)
for
the
Eu-
ropean call option becomes
the
following
boundary
condition for u(x,
T)
at
time
T =
0:
u(x
,
O)
= K
exp(α
x)
max(e
X
-
1,
0).
(ii) Show
that
the
boundary
condition
V(S
,
T)
=
max(K
- S,
O)
for
the
European
put
option becomes
fL)ldzdu=d2
(x ,y) =
(r
cos e,r sin
e)
with (r,
e)
εit
=
[0
,
R]
x
[0
,
2
作)
.
Recall
that
dxdy = rdedr.
Then
,
川旷
dxdy
工
flo
川价:叫
R
巾=作
R27
which is equal
to
the
area of a circle of radius
R.
口
Problem
4: Let
V(S
,t) =
exp(
一
αx
-
bT)U(X
,
T)
,where
L
(S
\ (T -
t)
σ2γ
-q
1
1~
(γ
-q
\2
x = In I
-:;:-;
I , T
='
~
,
α=
…
n
一~,
b=
I
一
n
十一
i
十一
τ
-飞
K
J"
2σ2
2'
飞
σ2
'2
J
俨
Problem
3: Use
the
change of variables
to
polar coordinates
to
show
that
the
area of a circle of radius R is 1f
R2
,i.e.,prove
that
164
Solution: Note
that
t = T if and only if T =
O.
Then
,
V(S
,
T)
=
exp(
一
α
x)u(x
,
O).
Here,x = In
(丢),
which can also be
written
as S = K
eX
(7.8)
Problem
6: Assume
that
the
function
V(S
,
I
,
t)
satis
自
es
the
following
PDE:
θVθ
V
1
θ
2V
θV
一十
S
一十一
σ
2S2
一一
+
rS
一
-
rV
=
O.
(7.10)
θtδ
I
'
2θ
S2
θS

166
CHAPTER
7.
MULTIVARIABLE
CALCULUS.
7.1.
SOLUTIONS
TO
CHAPTER
7
EXERCISES
167
(7.11)
By substituting
inω(7.10)
,
it
follows
that
oθVθ
V
1
<)_<)θ
2V
θV
=一一十
S
一一十一
σ
,c,
5
,c,
一一一十
r5
一一
-
rV
θtθ
I
'
2θ52θS
θHθ
H
1
'>
_,>
R
2
θ
2H
_
(θH\
S
一-十
S
一一十…
σ
于一一一十
γ
5IH-R
一~
1 -
r5H
θtθ
R
'
2--
5
θ R2
飞
θ
RJ
θ
H
1
叮叮
θ
2H
θH
S
一十
::'-(7".<l
5R
".<l
一丁十
5(1-
rR)
一
θ
t
'
2
山
LθR
By
dividi
吨
by
5,
we
conclude
that
H(R
,t)
satis
且
es
the
PDE
θ
H
1
叮叮
θ
2H
θH
37+rzRZ
否
E
十
(1
- r
R)
百五
0,
which
is
the
same as
(7.12).
口
Consider
the
following change of variables:
V(
川
)=5H
川
7where
R
=i
Show
that
H
(R
,t) satisfies
the
followi
吨
PDE:
θ
H 1
'>_'>θ
2H
θH
万
J+2σ
".<l
R
".<l
否
R2
+
(1-
rR)
否五口。
(7.12)
Note:
An
Asian call option pays
the
maximum between
the
spot price
5(T)
of
the
underlying asset
at
maturity
T and
the
average price of
the
underlying
asset over
the
entire life of
the
option,i.e.,
\liI/
T
JU
T
T
PI''''nu
--T
T
/III-\
x
a
m
Thus
,
the
value V (5,I,t) of
an
Asian option depends
not
only on
the
spot
price
5 of
the
underlying asset and on
the
time
t,
but
also on
the
following
random variable:
I(t)
= I 5(7)
d7.
JO
It
can be shown
that
V(5
,I ,
t)
satis
丑
es
the
PDE
(7.10). Similarity
sol
沁
u
叫
1
of
the
type
(7.11) are good candidates for solving
the
PDE
(7.10).
The
PDE
(7.12) satisfied by
H(R
,
T)
can
be
solved numerically, e.g., by using finite
differences.
Problem
7:
The
price of a non-dividend-paying asset is lognormally dis-
tributed. Assume
that
the
spot
price is
40
,
the
volatility is 30%,
and
the
interest rates are constant
at
5%.
Find
the
Black-Scholes values of
the
IT
Jv
I
put
options
0
丑
the
asset with strikes
45
,48 and
51
,
and
maturities 3 months
and 6 months.
For which of these options is
the
intrinsic value
max(K
- 5,
0)
larger
than
the
Black-Scholes value of
the
option (in which case
the
c
∞
orrespo
丑时
d
剑
i
丑
Arne
臼创
flca
缸
I
卫
1
put
is guaranteed
to
be worth more
than
the
European p
叫
?
Solution:
The
values of
the
out
options are summarized
in
the
table below:
S
豆豆
.
θ
t
'
S
纽纽一
θH
一
θRθIθ
R'
θHθRδ
H
(
I
\IθH
H+5
一一…一
=H+5
一一!一一
l=H
一一一一
θRθSθR
飞
52
J
~~
5
θR
δH
H-R
一一:
δ
R
J
θHθRθRθHθ
2H
θ
R
_
I
θ
2H
一一一一一一一一一
-
R
一一一一…
-
R
一一一一一
θRθSθSθRθ
R2
δ5
-
.L"
52
θ
R2
R
2
θ
2H
S
θ
R2'
Option
Type
Strike
Jv
laturity
Value
K-5
Put
45
6 months 5.8196
5
Put
45
3 months
5.3403 5
Put
48
6 months
8.0325 8
Put
48
3 months 7.8234
8
Put
51
6 months
10
.4
862
11
Put
51
3 months
10.5476
11
Sol
仰
on: Let
V(5
,I ,t) = 5
H(R
,t),
with
R
=~'
Using Chain Rule,
we
白缸
fin
丑
l
that
θ
2V
δ52
In
general,
the
values of
deep-in-the
money European
put
options are
lower
than
the
premium K - 5. This feature was observed for
the
options
priced here:
the
values of
the
51-puts
and
of
the
three months
48-put
are
below their intrinsic value
K - 5.
Also, note
th
创
for
the
51-puts
(i.e., for deep
in
the
money puts),
the
values of
the
short
dated
options are higher
than
the
values of
the
long
dated

168
CHAPTER
7.
l\
1ULTIVARIABLE
CALCULUS.
7.1.
SOLUTIONS
TO
CHAPTER
7
EXERCISES
169
(7.18)
(7.17)
(7.16)
8K
E~
~;.,~
N(d
2
)
B\()
B
N(d
2
)
θ
出
8K
问丁
-zSKB
可
LNf(d2)
一
θB
1 I
d~
\2
8K
li
囚一二
eXD
I -
-~.4
I
.一一
τ
B\
、
0 飞
12
1f
品\
~J
B
σ
飞
IT
28K..
I
d~
\
τF
王三
Ulr~
exp ( -
~.4
-
I
口
(B)
)
σ
〉乙
1f
T
B
\J\~
" }
As B
\、
0
,
the
term
一手-
In(B) is on
the
。阳.
of
一(l
n(
B))2
,
and
阳
efore
I
-3
2 \
』史坷吃~~←一
7?
一
-In
峭
n
From
(σ7.16
叫
6
创)
a
叫
(σ7.17η)
we
直nd
that
8K
问~~~
N(d
2
)
= 0,
and,
fro
皿
(7.14)
,
(7.15), and (7.18),
we
conclude
that
(
_.
_.
_ _
_,
_ , 8K \
U~
V(8)
=
h~
(0(8)
-
BN(d
1
)
十一:;-
N (d
2
))
= 0 (8)
.口
\O\.0
飞
B
_.
'--"'I
J
plain vanilla call
with
strike K when B
\、
O.
For simplicity, assume
that
the
underlying asset does
not
pay dividends
and
that
interest rates are zero.
Sol
毗
on:
Let t = 0 in formula (7.13). For r = q = 0,
we
find
that
α=-i
Therefore,
the
value of
the
down-and-out
call is
8
_.
I
β2\
V(8)
=
0(8)
一;,
0
I:
)
B
飞
8
J
81B
2
\
0(8)
一一(
~n
N(d
1
) -
KN(d
2
) I
B
飞
8
-
,--.J.
I
--_.
'-"'I
J
8K
0(8)
-
BN(d
1
) +
~~~
N(d
2
) ,
(7.14)
B
where
0(8)
is
the
value of
the
plai
口
vanilla
call
wi
出
strike
K and
l
叫到十卓
T
I
川剧
_
~2T
d
1
=
γ
一/一
-and
d?
=
γ 一/一-
σ
飞
IT
…
σ
飞
IT
Note
that
0 <
N(d
1
)
<
1.
Then
,
且也
BN(d
1
)
=
O.
(7.15)
Using I'H6pital's rule
,
we
obtain
that
whereα=
手-
~'
to
find
the
value of a six months
down-and-out
call on a
non-dividend-paying asset with price following a lognormal distribution
with
30% volatility
and
spot
price 40.
The
barrier is B =
35
and
the
strike for
the
call is K =
40.
The
risk-free interest
rate
is constant
at
5%.
Solution:
The
value of
the
down-and-out
call is
$3.398883.
口
OBs(8)
-
max(8
- K ,
O)
is obtained for 8 = K , where
OBs(8)
is
the
Black-Scholes value of
the
plain
vanilla European call option with strike
K and spot price
8.
Solution: Let
j(8)
=
OBs(8)
-
max(8
- K ,
O).
It
is easy
to
see
that
J
OBs(8)
,
if
8
三
K;
f(S)=i
cm(S)-S+K7if
S
>K
Problem
9: Use
the
formula
IB
\2α
I
B
2
\
V(8
,K ,t) =
0(8
,K ,
t)
一(计
o
\
~
,K ,t ) ,
(7
叫
Problem
10:
Show
that
the
value of a
down-and-out
call
with
barrier B
less
than
the
strike K of
the
call, i.e., B < K , converges
to
the
value of a
lThis
premium
is
also called
the
time value of
the
option.
Note
that
j
(8)
is a
continωus
function,
but
it is
not
differentiable
at
8 =
K.
For 8 < K ,
the
function
j(8)
is
the
value of a call
with
strike K ,
a
缸
an
丑
1
tr
扭
lerefore
is
ir
丑
lcreasir
卫
19.
For 8 > K ,
we
find
that
1'
(8)
=
~(CBS)
- 1 =
e-
qT
N(d
1
)
- 1 <
N(d
1
)
… 1
=-N(-d
1
)<0
,
and
therefore
the
function
j(8)
is decreasing.
We conclude
that
j(8)
has
an
absolute maximum point
at
8 =
K.
口
Problem
8: Show
that
the
premium
1
of
the
Black-Scholes value of a Euro-
pean
call option over its intrinsic value max(8 - K ,
0)
is largest
at
the
money.
In
other
words, show
that
the
maximum value of
options. This is
to
be
expected; for example, if
the
spot
price is 0,
the
value
of a European
put
is K
e-
r1
\
in which case longer
dated
puts
are worth less
than
short
dated
ones.
口

170
CHAPTER
7.
MULTIVARIABLE CALCULUS.
7.2.
SUPPLEMENTAL EXERCISES
171
Problem
11:
Compute
the
Delta
and
Gamma
of a
down-and-out
call
with
B<K.
Solution: We rewrite formula (7.13)
to
emphasize
the
dependence
ofthe
value
V(8)
of
the
down-and-out
call
0
日
the
spot
price 8 of
the
underlyi
吨
asset
as follows:
B
2
α
(B
2
\
V(8)
=
C
B
s(8)
一
~')n
CBS
(
~n
).
(7.19)
8
2α
飞
8
}
By
differentiati
吨
(7.19)
with respect
to
8 ,
we
obtain
that
2α
B2
α
(B2
\
B2
α+2
.
,_.
•
(B2
\
~(V)
=
~(CBs)(8)
+
一一
-CBsl-i
十一丁
~(CBS)
(一)
8
2α
+1
飞
8
)
υj
飞
j
where
~(CBS)(X)
=
e-
qT
N(d
1
(x)),with
l
丑(是)
+
(γ-q
十号
)T
d
1
(x)
=
\一/
7.2
Supplemental
Exercises
1.
Compute
J
!n
xdX
where
D =
{(川
D
n
a
m
o
d
e
A?U
QU
ny
a
m
u-z
,
TLU
n
BU
UU
z
--
QU
5]
af-
-n
×
a
pe
DE-si
n-g
an
C41
c
euu
hI
TK
MD
(7.20)
2.
Which number is
larger
,俨
or
7r
e
?
3.
Let
叩)
:
[0
,∞)→
[0
,∞)
be
two continuous functions with positive
values. Assume
that
there exists a constant M > 0 such
that
2α(2α
十
1)B
2
α
(B
2
\
r(V)
=
r(CBs)(8)
一例。
C
BS
(
一)
8
'2
α
十万
飞
8 J
(4α
+
2)B
2
a+2(B
2
\Bh+4/\
~(CBS)
\
~
)一百
a+4
r(CBs)
(τ)
,
u(x)
三
M+fa
叫
t)v(
忖
\f
x~O
Show
that
u(x)
三
M
叫俨
(t)
dt)
,
If x
?:
0
where
Hint: Investigate
the
monotonicity of
the
fu
日
ction
e-
qT
( d
1
(x)2
\
r(cBS)(x)
=
~exp
(
_
v'
1
':
J
I
x
σ
飞/三7r
1\
,e,
/
with
d
1
(x)
given by
(7.20).
口
\It's//
,
,
d
,
?b
u
z
PI'120
/III-\
D&
x
e
,
TLU
/,
11\
A'LU
U
Z
V
J
/III-\
Note: This is
a
version of
Gronwall's
inequality
,
and
it
is
needed
,
e.g.
,
to
prove
the
uniqueness of
the
solution
of
an
initial value
problem
for
ordinary differential
equations.
4.
What
does
the
boundary
condition
V(B
,
t)
=
R for a
down-and-out
call
with
barrier
B
and
rebate
R
>
0
correspond
to
for
the
function
也
(x
,
T)
defined
as
follows:
V(8
,
t)
二
exp(
一
α
x
-
bT)U(X
,
T)
,
where
(8\
(T
-
t)
σ2γ
-q
1
1-._
(γ
-
q
,
1\2
,
2q
x
=
In
I
=-_
I.
T
二
龟
α=
一一「一丁、
b=l
一"十丁
1+
一
τ·
飞
K
J
I
2σ
:L
~'\σ
:L
~J
σ4

aωsaf
旬
un
肌
ct
杜
10
∞丑
of
σ
町
irr
η1
以
K).
Note:
The
values of Asian options with continuously sampled geometric
average satisfy
the
PDE
(7.21).
6. One way
to
see
that
American calls on non-dividend-paying assets are
never optimal to exercise
is
to note
that
the
Black-Scholes value of
the
European call
is
always greater
than
the
intrinsic premium S - K ,for
S>K.
Show
that
this argument does not work for dividend-paying assets.
In
other words, prove
that
the
Black-Scholes value of
the
European call
is
smaller
than
S - K for S large enough, if
the
underlying asset pays
dividends continuously
at
the
rate
q > 0 (and regardless of how small
q is).
173
[[~去
ω
H[
VS
dS
)
([忐
dt)
i(;
二1:)(剖)
f
儿
z
伽
J
!n
XdX
D =
{何?们}R
2
Ix
~
0,
1
三时
2
,
1
才三
2}
Then
,
Problem
2: Which number is
larger
,♂
or
7r
e
?
Solution: We show
that
7r
e
<♂.
By taking
the
natural
logarithm,it
is
easy
to
see
that
l
叫7r)
/ 1 _ ln(e)
作
e<
♂仁中
eln(
作)
<作仁学一一<一一
-7·
(722)
7r
e e
Sol
仰
on:
The
change of variables 8 =
xy
and t =
~
is equivalent
to
x-~andY=
而?
when
x
主
o
and y
~三
O.
This change of variables maps
the
domain D into
the
recta
吨
Ie
n=
[1
,
2]
x
[1
,
2].
It
is
easy
to
see
that
|θzβ
钊
θzβ111
dxdv _
I:~
~~i1
一一一立
I
d8dt
IJ
-
Iθsθtθtθ81
|土豆-
(-均丘[出
dt
2
VSt
20 \
2t0)
2ft
i
dsdt
2t
where
Problem
1: Compute
7.3
Solutions
to
Supplemental
Exercises
7.3.
SOLUTIONS
TO
SUPPLEMENTAL
EXERCISES
CHAPTER
7.
Iv
IULTIVARIABLE
CALCULUS.
7.
For
the
same
maturity
,options with different strikes are
traded
simul-
taneously.
The
goal of this problem
is
to
compute
the
rate
of change of
the
implied volatility as a function of
the
strike of
the
options.
In other words
, assume
that
S ,T , q and r are given, and let C
(K)
be
the
(known) value of a call option with
maturity
T and strike
K.
As-
sume
that
options with all strikes K exist. Define
the
implied volatility
σ
imp(K)
as
the
unique solution
to
C(K)
=
CBs(K
,
σ
问
(K))
,
where
CBs(K
,
σ
imp(K))
=
CBs(S
,K ,
T
,
σ
imp(K)
,
r
,
q)
represents
the
Black-Scholes value of a call option with strike K on an underlying
asset following a lognormal model with volatility
向
mp(K).
Find an
implicit differential equation
satis
自
ed
byσ
问
(K)
,
i.e.,
fi
日
d
δσ
imp(K)
θK
5.
Assume
that
the
function
V(S
,I ,t) satisfies
the
PDE
θVθ
VI')
~')θ
2V
δV
一+
InS
一十一
σ
乎一一
+
rS
一
-
rV
=
O.
(7.21)
δtθ
I
2θ
S2
θS
Consider
the
following change of variables:
I +
(T
-
t)
InS
V(S
,I ,t) =
F(y
,
t)
, where y = - ,
,-
T
Show
that
F(y
,t)
satis
且
es
the
followi
吨
PDE:
主主十
σ
2(T
-
t)2
~2:
+
(r
一到丘
t
8F
rF
= 0
δ
t
2T2
8y2
\2)
Tθu
172
