Станішевський С.О. Вища математика. Конспект лекцій. Модуль 1

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ХАРКІВСЬКА НАЦІОНАЛЬНА АКАДЕМІЯ МІСЬКОГО

ГОСПОДАРСТВА

С.О.Станішевський

ВИЩА МАТЕМАТИКА

КОНСПЕКТ ЛЕКЦІЙ

Модуль 1

Харків – ХНАМГ – 2009

Вища математика

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

1

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ХАРКІВСЬКА НАЦІОНАЛЬНА АКАДЕМІЯ МІСЬКОГО ГОСПОДАРСТВА

С.О.Станішевський

ВИЩА МАТЕМАТИКА

КОНСПЕКТ ЛЕКЦІЙ

Модуль 1

Напрям підготовки 6.060101 – «Будівництво»

Харків – ХНАМГ – 2009

Вища математика

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

2

УДК 517.2 + 517.51

С.О.Станішевський. Вища математика. Конспект лекцій. Модуль 1.

Напрям підготовки 6.060101 – «Будівництво». – Харків: ХНАМГ, 2009.

– 151 с.

Конспект містить двадцять вісім лекцій з вищої математики.

Зміст яких відповідає діючої програмі першого модуля дисципліни для

бакалаврів денної та заочної форм навчання за фаховим напрямом під-

готовки 6.060101 «Будівництво».

В лекціях наведено стислі теоретичні відомості з аналітичної

геометрії на площині та у просторі, лінійної та векторної алгебри, ди-

ференціального та інтегрального числення функцій однієї змінної, які

підкріплені відповідними прикладами.

Рецензент: д-р ф.-м. наук, професор А.І.Колосов

Рекомендовано кафедрою вищої математики,

протокол № 6 від 27.01.09.

Вища математика

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

3

ПЕРЕДМОВА

Даний конспект є першою частиною цикла лекцій з вищої мате-

матики, які автор читає на факультеті інженерної екології міст Харків-

ської національної академії міського господарства (ХНАМГ).

Програма курсу вищої математики для бакалаврів денної та за-

очної форм навчання за фаховим напрямом підготовки 6.060101 «Буді-

вництво» складається з трьох модулів, які розраховані на 14,5 кредитів

або 522 години.

Для денної форми навчання ці години розподіляються так: 138 –

лекції; 156 – аудиторні практичні заняття; 228 – самостійна робота по

засвоєнню лекційного курсу.

Для заочної форми навчання відповідно: 30 – лекції; 24 – прак-

тичні заняття і 468 – самостійна робота.

Кожний модуль містить по три залікових модуля, кожний з яких

охоплює відповідні теми курсу.

Програмою за першим модулем (210 годин) охоплені такі розді-

ли вищої математики, як аналітична геометрія на площині та у просто-

рі, лінійна та векторна алгебра, диференціальне та інтегральне числен-

ня функцій однієї змінної.

Кожна лекція має відповідні приклади, що дає змогу студентам

всіх форм навчання самостійно опановувати курс вищої математики.

Нумерація рисунків і формул має дві цифри. Перша цифра вка-

зує на порядковий номер теми, а друга – номер у темі.

Зауваження і пропозиції щодо конспекту лекцій надсилайте на

кафедру вищої математики за адресою: м. Харків, вул. Революції, 12,

ХНАМГ.

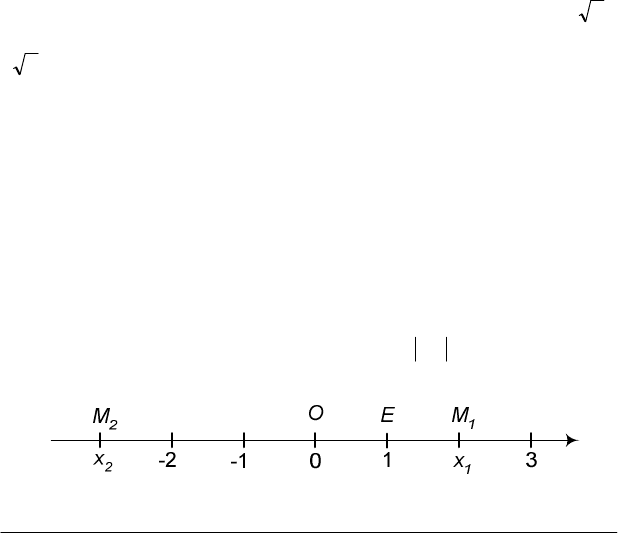
Вища математика

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

4

ТЕМА 1. АНАЛІТИЧНА ГЕОМЕТРІЯ НА ПЛОЩИНІ

ЛЕКЦІЯ № 1

Дійсні числа. Число - це найважливіше математичне поняття,

яке з'явилось у давнину і на протязі тисячоліть удосконалювалось та

узагальнювалось.

1. Дійсні числа охоплюють: натуральні числа - це числа 1, 2,

3,...,n, які використовують для лічби; цілі числа - це числа утворені

внаслідок додання до множини всіх натуральних чисел числа нуль і

від'ємних цілих чисел (...,-3,-2,-1,0,1,2,З,...); раціональні числа - це такі

числа, які можна подати у вигляді p/q, де р належить до множини ці-

лих чисел, а q - до множини натуральних чисел; ірраціональні числа -

це такі числа, які не можна записати у вигляді p/q.

Раціональні числа можна записати у вигляді десяткового дробу

(скінченого або нескінченного періодичного), а ірраціональні числа

можна записати у вигляді нескінченного неперіодичного десяткового

дробу.

Приклад: число 2/3 = 0,6666...= 0,(6) - раціональне; число

2

-

ірраціональне, його можна записати раціональним числом:

≈2

1,414213...

Для кожної множини чисел введено позначення: N – натуральні;

Ζ - цілі; Q - раціональні; S – ірраціональні; R – дійсні.

Отже, до множини Q належать множини Ζ та N, а множина R

утворена з об'єднання множин Q та S.

2. Дійсні числа упорядковані по величині, тобто для кожної па-

ри дійсних чисел х та у має місце одне і тільки одне із співвідношень:

х<у, х = у, х>у

Дійсні числа можна відобразити точками числової прямої (осі).

Числовою віссю називають нескінченну пряму (рис.1.1), на якій узято:

1) довільну точку О, яку звуть початком координат;

2) додатний напрям, який позначаємо стрілкою;

3) масштаб для вимірювання довжин (

ОЕ

– одиниця вимірю-

вання).

Риc.1.1

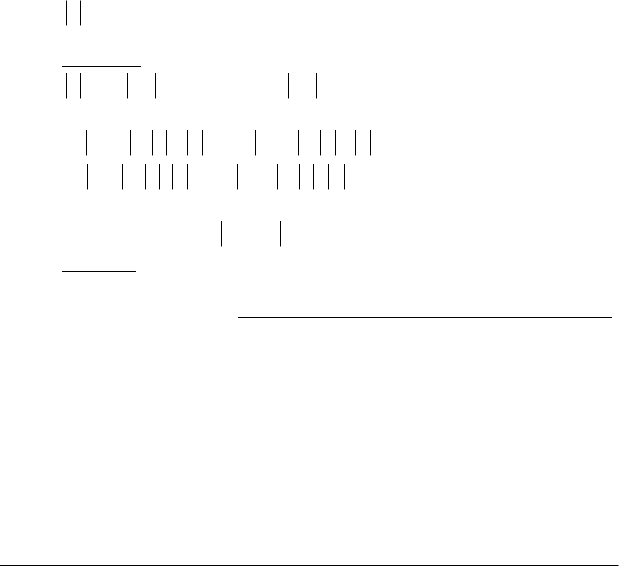
Вища математика

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

5

Якщо число х

1

додатне, то його зображує точка М

1

, яка лежить

праворуч від точки О на відстані ОМ

1

= х

1

; якщо число х від'ємне, то

його зображує точка М

2

, яка лежить ліворуч від точки О на відстані

ОМ

2

= –х

2

. Точка О відображує число нуль. Отже, кожне дійсне число

відображається визначеною точкою на числовій вісі, а кожна точка

числової вісі є відображенням тільки одного дійсного числа (раціона-

льного або ірраціонального).

Таким чином, між дійсними числами і точками числової вісі іс-

нує взаємно однозначна відповідність. Нагадаємо (без доведення) важ-

ливу властивість дійсних чисел: між двома довільними дійсними чис-

лами знайдуться як раціональні, так і ірраціональні числа.

Отже, координатою точки М

0

, що лежить на координатній вісі,

називають число х

0

, яке визначається рівністю х

0

= ±|ОМ| / |ОЕ|; знак

'+' беруть, якщо M

0

розташоване праворуч і '–' - ліворуч від точки О.

3. Абсолютним значенням (або модулем) числа а називають чи-

сло, яке позначають |а| і обчислюють за правилом







<−

≥

=

.0 а якщо ,а

,0а якщо ,а

а

Приклад. Знайти абсолютні значення чисел 4 та –3.

33 ;44 =−=

тому, що

(

)

333 =−−=−

.

Нагадаємо деякі властивості абсолютних величин:

а) ухух

+≤+

; б) ухух

−≥−

;

в) ухух

⋅=⋅

; г) у

/

ху

/

х

=

.

4. Відстань d між точками М

1

і М

2

з координатами х

1

і х

2

обчис-

люють за формулою

12

хх

d −=

.

Приклад. Знайти відстань між точками: М

1

(–3); М

2

(2).

d = |–3–2| = |–5| = 5.

Метод координат. Прямокутна система координат на площині.

Візьмемо на площині дві взаємно перпендикулярні прямі. Далі їх бу-

демо називати координатні вісі Ох і Оу. Точку перетину осей позна-

чимо через

О

і на кожній вісі відкладемо одиничні відрізки

1

ОЕ

і

2

ОЕ

(рис. 1.2).

Вісі Ох і Оу упорядкуємо так: якщо вісь Ох повернути навколо

точки О на кут

2/

π

проти руху стрілки годинника, то вона співпаде з

віссю Оу. При цьому точки Е

1

і E

2

теж збігаються тому, що

1 2

|

ОЕ

| |

ОЕ

| 1

= =

. Прийнято називати вісь Ох віссю абсцис, а вісь Оу –

Вища математика

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

6

віссю ординат.

Отже, площину з побудованою системою координат звуть коор-

динатною площиною.

Розглянемо дві задачі у методі координат.

1. Ділення відрізку у даному відношенні. Нехай А(х

1

,у

1

) і В(х

2

,у

2

)

дві точки на координатній площині Oxy (рис.1.2).

Проведемо пряму АВ і встановимо на ній додатний напрям від А

до В. Нехай M(x,y) - точка прямої АВ. Якщо Μ лежить між точками А i

В, кажуть, що вона ділить відрізок [АВ] внутрішнім чином; якщо точка

Μ лежить праворуч або ліворуч від точок А і В - кажуть, що точка Μ

ділить відрізок [АВ] зовнішнім чином. Назвемо відношенням, у якому

точка Μ ділить відрізок [АВ], число λ, яке знаходимо за правилом

λ = AM/MB,

Рис. 1.2

якщо відомі координати точок А, В і М. Коли ж маємо число λ, треба

знайти координати точки М. Число λ

0

>

, якщо відрізок ділиться внут-

рішнім чином, і λ

0

<

у другому випадку (відрізки AM і MB мають про-

тилежні напрями). λ = 0 коли A = B (точки збігаються). Розглянемо

проекції відрізка [ΑΒ] на вісь Ох (рис.1.2).

Тоді: λ = (х – х

1

)/(х

2

– х), звідки x = (х

1

+ λx

2

)/(1+λ).

Зробивши те саме з у-ю координатою, матимемо:

у =(у

1

+ λy

2

)/(1 + λ).

Приклад. Знайти координати точки М(x,y), якщо А(1, 2),

В(–1, –2) і λ = 1/2.

Рішення:

;3/1)2/3/()2/1()2/11/())1(2/11(

х

==+−+=

•

у

2

у

1

х

1

х

2

х

А

М

В

О

Е

1

φ

0

С

N

Вища математика

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

7

;3/2)2/3/(1)2/11/())2(2/12(

у

==+−+=

Відповідь: М (1/3, 2/3).

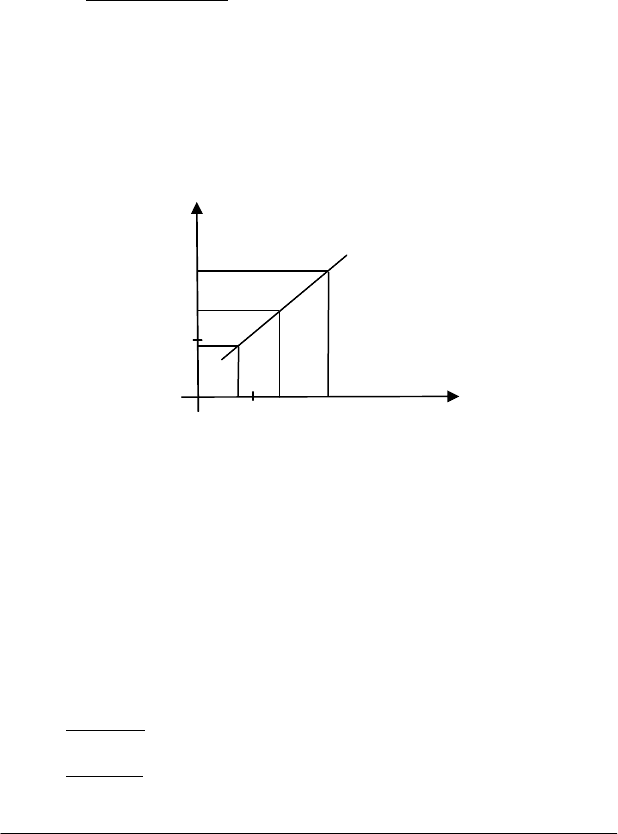
2. Площа трикутника. Відомі координати вершин

АВС

∆

: А(х

1

,

у

1

), В(х

2

, у

2

) і С(х

3

,.у

3

) (рис.1.3). Знайти площу ∆ΑΒС.

Рис. 1.3

Нехай |CA|=d

1

, |CB|=d

2

і φ - кут між відрізками [АС] і [ВС]. Ві-

домо, що площа трикутника обчислюється за формулою:

1 2

S 1/ 2|d d sin |

∆

ϕ

=

,

де

12

ααϕ

−=

. Перетворимо вираз:

(

)

1 2 2 1

1/ 2 d d sin

α α

− =

1 2 2 1 2 1

1/ 2 d d (sin cos cos sin )

α α α α

= − =

1 1 2 2 2 2 1 1

1/ 2 d сos d sin d сos d sin

α α α α

= − =

1 3 2 3 1 3 2 3

АВС

1/ 2 ( х х )( у у ) ( у у )( х х ) S

∆

= − − − − − =

Тут скорочено позначені проекції сторін трикутника на відповідну

вісь:

Ох 1 1 1 3

Пр АС d cos х х

α

= = −

;

Оу 1 1 1 3

Пр АС d sin у у

α

= = −

;

Ох 2 2 2 3

Пр ВС d cos х х

α

= = −

;

Оу 2 2 2 3

Пр ВС d sin у у

α

= = −

.

Приклад. Обчислити площу

∆

АВС, де: А(1, 2),В(-2,3) і С(0,5).

42/8|)52)(02()53)(01(|2/1S

АВС

==−−−−−−=

∆

од

2

.

Наслідок. Якщо

0)хх)(уу()уу)(хх(

32313221

=−−−−−

, то

точки А, В і С лежать на одній прямій.

y

1

B

A

C

φ

α

2

α

1

y

3

x

2

x

1

x

3

0

y

2

Вища математика

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

8

ЛЕКЦІЯ № 2

Лінії першого і другого порядку на площині. Візьмемо на коор-

динатній площині деяку лінію і її довільну точку. Якщо ця точка буде

переміщатися по цій лінії, то її координати х і у будуть змінюватися,

залишаючись, однак, зв'язаними деякими умовами, які характеризують

точки лінії. Виходячи з цих умов, лінії на площині відповідатиме деяке

рівняння F(x,y)=0.

Якщо F(x,y) - многочлен першого степеня, то лінія, яка визнача-

ється цим рівнянням, є лінія першого порядку. Лінія першого порядку

- це пряма.

Якщо F(х,y) - многочлен другого степеня, то лінія, яка визнача-

ється цім рівнянням, є лінія другого порядку.

Лінія другого порядку залежно від коефіцієнтів визначатиме:

коло, еліпс, гіперболу або параболу, а при деяких значеннях коефіцієн-

тів – точку або дві прямі (останні випадки звуть виродженими).

Лінії першого порядку на площині. Щоб скласти рівняння пря-

мої треба якимось чином задати умови, що визначають положення її

відносно прямокутної системи координат.

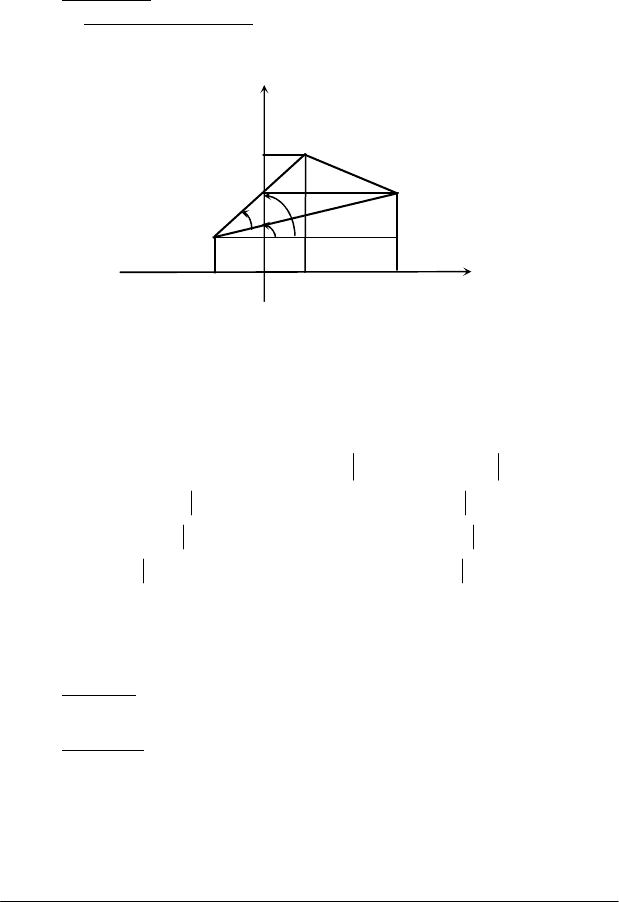
Рівняння прямої з кутовим коефіцієнтом. Назвемо кут нахилу

прямої до вісі Ох той кут, на який треба повернути вісь Ох проти стрі-

лки годинника, щоб вона збіглась з даною прямою.

Тангенс кута нахилу прямої до вісі Ох називають кутовим кое-

фіцієнтом прямої.

Якщо кутовий коефіцієнт дорівнює нулю, то пряма паралельна

вісі Ох. При додатному значенні коефіцієнта кут нахилу прямої до вісі

Ох буде гострим, при від'ємному значенні - кут тупий. Пряма, перпен-

дикулярна до вісі Ох, не має кутового коефіцієнта.

Розглянемо рівняння Ах + Ву + С = 0. (1.1)

Розв'яжемо його відносно змінної у:

у = (–А/В) х – С/В, це можливо при В

≠

0.

Якщо позначити: –A/B=k; –C/B=b, то останнє рівняння матиме

вигляд

у = kx + b, (1.2)

який має назву: рівняння прямої з кутовим коефіцієнтом. Якщо х=0,

маємо у=b - це відрізок, який відсікає дана пряма на вісі ординат. Як-

що α - кут, який утворює пряма з віссю Ох, то k=tgα.

Рівняння (1.2) можна скласти безпосередньо з рис.1.4 через від-

повідні проекції (Пр) на вісі.

Так:

Ох

BN

ОР Пр ВМ х

= = =

;

Оу

QB

МN Пр ВМ у b

= = = −

.

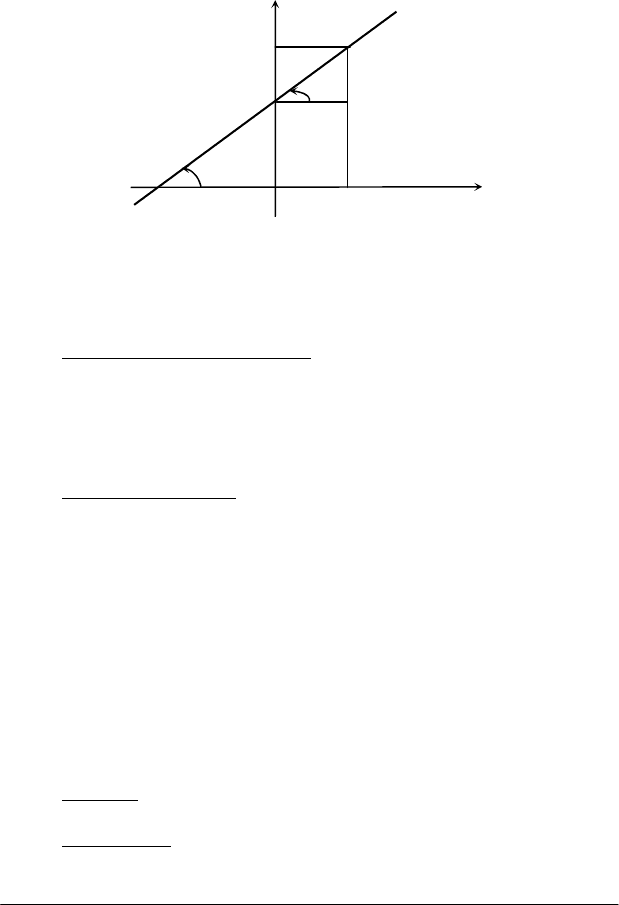
Вища математика

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

9

Рис. 1.4

З

BNM

∆

знаходимо:

b)/х-(уQB/OPMN/BNtg

=

α

. Розв'яза-

вши останнє співвідношення відносно у, маємо (1.2).

Рівняння прямої у відрізках. Якщо рівняння (1.1) перетворити

таким чином:

х/(–С/А) + у/(–С/В) = 1 і позначити: –С/А = а; –С/В = b, то ма-

тимемо рівняння прямої у відрізках

х/а + у/b = 1 . (1.3)

Останнє можливо коли

0А

≠

,

0В

≠

і

0С

≠

.

Дослідження прямої (1.1):

а) нехай С=0. Рівняння має вигляд Ах+Ву = 0 і визначає пряму,

яка проходить крізь початок координат;

б) нехай Α = 0. Рівняння має вигляд Ву + С = 0 i визначає пряму,

яка паралельна вісі абсцис;

в) нехай В=0. Рівняння має вигляд Ах + С = 0 i визначає пряму,

яка паралельна вісі ординат;

г) нехай В=0, С=0. Рівняння має вигляд Ах=0 i при

0А

≠

визна-

чає вісь Оу;

ж) A=0, С=0. Рівняння має вигляд Bу = 0 і при

0В

≠

визначає

вісь Ох.

Таким чином усяке рівняння першого порядку відносно змінних

x і у визначає пряму лінію.

Приклад. Перетворити рівняння 2х – 3у + 6 = 0 до вигляду (1.2) та

(1.3).

Розв'язання:

а) 3у = 2х + 6; у = (2/3)х + 6/3; у = 2х/3 + 2;

б) 2х – Зу = –6; 2х/(–6) – Зу/(–6) = 1; х/(–3) + y/2 = 1.

y

B

A

α

x

a

0

Q

N

M(x,y)

P

b

α

Станішевський С.О. Вища математика. Конспект лекцій. Модуль 1

Подождите немного. Документ загружается.