Станішевський С.О. Вища математика. Конспект лекцій. Модуль 1
Подождите немного. Документ загружается.


Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
30
1, є неперервною і монотонною, тобто вона має обернену функцію; її
звуть арксинусом і записують х = arcsiny. Позначивши незалежну
змінну буквою х, а залежну – буквою у,
далі писатимемо
у = arcsinх. Область її визначення - проміжок [–1, 1], область зміни –
проміжок
]2/ ,2/[
ππ
−
. Графік подано на рис. 2.13.
Рис. 2.13 Рис. 2.14 Рис. 2.14 Рис. 2.15
у = arccosx. Виділимо на числовій вісі Ох проміжок
] ,0[
π
. На
цьому проміжку функція у = cosх спадає від 1 до –1, є неперервною і
монотонною, тобто вона має обернену функцію; її звуть арккосинусом
і записують х = arccosy. Позначивши незалежну змінну буквою х, а
залежну - буквою у, далі писатимемо у = arсcosx. Область зміни про-
міжок
] ,0[
π
;
область визначення - проміжок [–1;1]. Графік подано на
рис. 2.14.
у = arctgx. Виділимо на числовій вісі проміжок
]2/ ,2/[
ππ
−
.
На цьому проміжку функція відповідає умовам існування у неї обер-
неної функції. Функцію обернену до у = tgx звуть арктангенсом і запи-
сують х = arctgy, де у - незалежна змінна, а х - залежна. Позначивши
незалежну змінну буквою х, а залежну - буквою у, далі писатимемо у =
arctgx. Область визначення - вся числова пряма; область зміни - про-
міжок
]2/ ,2/[
ππ
−
. Графік подано на рис. 2.15.
у = arcctgx. Виділимо на числовій осі Ох проміжок
] ,0[
π
. На
цьому проміжку функція у = ctgx відповідає умовам функції, яка має
обернену. Цю функцію звуть арккотангенсом і записують х = arcctgy,
де у - незалежна змінна, а х - залежна. Позначивши, незалежну змінну
буквою х, а залежну - буквою у, далі писатимемо у = arcctgx Область
визначення - вся числова пряма; область зміни - проміжок
] ,0[
π
.
Графік функції у = arcctgx подано на рис. 2.16.
-1
1
у
х
π/2
0
-π/2
-1
1
у
х
π/2
0
π
у
х
π/2
0
-π/2
π/2
у
х
0
π

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
31
Складна функція. Нехай у - f(х) - числова функція з областю ви-
значення D(f) і областю аміни E(f), z = g(y) - числова функція, задана на
множині E(f) або деякій її підмножині, з областю зміни E(g). Відповід-
ність, яка відносить кожному даному числу х з множини D(f) єдине
число у з множини E(f), a числу у - єдине число z з множини E(g) звуть
складною функцією і записують
z = G(f(x)).
Більшість функцій, які вивчають у математиці, можна розгля-
дати як складні функції.
Приклад. Функцію
1
х
z −=
можна записати:
ху
=
; z = y –1.
Операція "функція від функції", може робитись не один, а будь-
яке скінчене число разів.
Приклад. Функція у = lg(sin(x
2
+ 1)) утворюється внаслідок та-
ких операцій (визначення таких функцій);
1
х
2
+=
ν
,
vsinu
=
,
gu1у
=
.
Елементарна функція. Елементарною функцією зветься функція,
яка може бути задана однією формулою у = f(x), де праворуч записано
вираз, складений із основних елементарних функцій і сталих величин
за допомогою скінченого числа операцій додавання, віднімання, мно-
ження, ділення та узяття "функції від функції". Таким чином, елемен-
тарні функції є функції, які задані аналітично.
Приклад. Функція
)arctgx
х
10/()tgx2
х
4
х
(lg
у
х
3
+−++=
, є
елементарною.
Приклад. Функція у =
⋅
⋅
⋅
321
…
п
⋅
= n! не є елементарною, тому
що число операцій змінюється із змінною n. Читається "ен факторіал".
Алгебраїчні функції.
Ціла раціональна функція або многочлен
n
1n
1
n
0
а
...
хахау
+++=
−
,
де
n10
а
,...,
а
,
а
- сталі числа, які є коефіцієнтами; n - ціле додатне чис-
ло, яке має назву степінь многочлена. Зрозуміло, що ця функція визна-
чена і неперервна при будь-якому
R
х
∈
.
Приклад. у = ах + b - лінійна функція. у = ах
2
+bх+с - квадрати-
чна функція
)0а(
≠
. Ці функції розглядалися раніше.
Дробово-раціональна функція. Ця функція визначається як від-
ношення двох многочленів:
)b...
х
b
х
b/()
а
...
хаха
(
у
m
1m
1
m
0n
1n
1
n
0
++++++=
−−
.
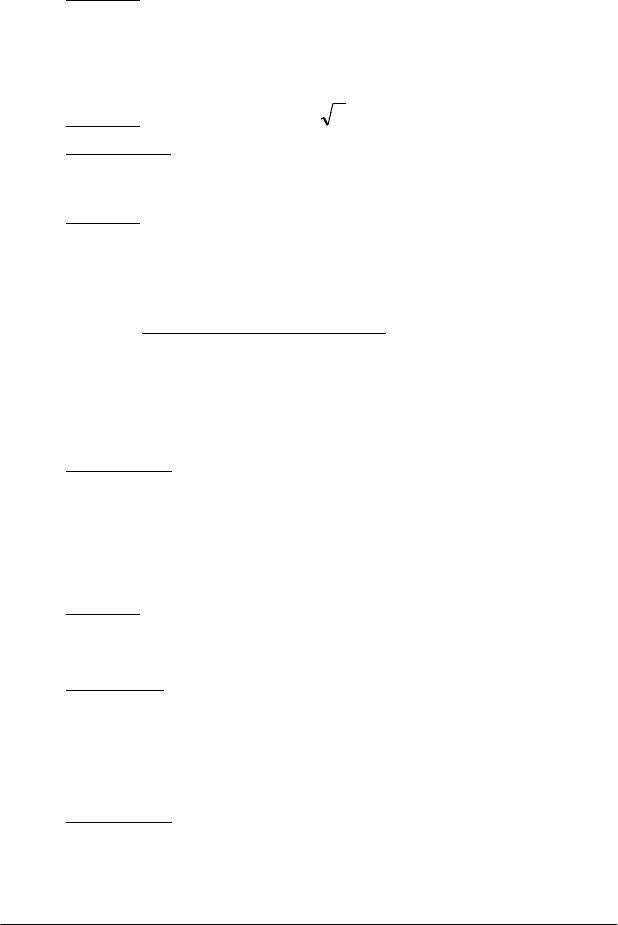
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
32
Приклад. Функція у = а/х,
)0х ,0а(
≠
≠
виражає обернено про-
порційну залежність.
Ірраціональна функція. Якщо у функції у = f(х) має місце підне-
сення до степені з раціональним дробовим показником, то вона є ірра-
ціональною.
Приклад. Функція
)
х
51/()
хх
2(
у
22
++=
є ірраціональна.
Зауваження. Розглянуті три види алгебраїчних функцій не виче-
рпують усіх алгебраїчних функцій. Функції, які не є алгебраїчні, звуть
трансцендентними.
Приклад. Функція у = cosx + 10
х
є трансцендентна.
ЛЕКЦІЯ № 6
Границі. Границя змінної величини. Будемо розглядати упоряд-
ковані змінні величини, які змінюються спеціальним чином, який ви-
значається термінами "змінна величина прямує до границі". Далі по-
няття границі змінної (функції) буде мати фундаментальне значення,
тому що з ним безпосередньо зв'язані основні поняття математичного
аналізу: похідна, інтеграл та ін.
Визначення. Стале число а є границею змінної величини х, якщо
для кожного наперед даного довільно малого числа
0
>
ε
можна вка-
зати таке значення змінної х, що всі наступні значення змінної будуть
задовольняти нерівності |х - а| <
ε
.
Якщо число а є границя змінної величини х, то кажуть, що х
прямує до границі а, і пишуть
а
х
→
або lίт x = а.
Приклад. Змінна величина x послідовно набуває значення:
11
х
1
+=
,
2/11
х
2
+=
,
3/11
х
3
+=
,…
n/11
х
n
+=
,…
Довести, що змінна величина має границю а = 1.
Розв'язання. За визначенням:
n/1|1)n/11(||1
х
|
n
=−+=−
.
Для будь-якого довільно малого
0
>
ε
всі наступні значення
змінної, починаючи з номера n, де
ε
<
n/1
, буде виконуватись нерів-
ність
ε
<− |1
х
|
n
, що і треба було довести.
Зауваження:
а) границя сталої величини є сама стала величина;
б) змінна величина не може мати дві границі;
в) не кожна змінна величина має границю.
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
33
Границя функції. Нехай функція f(х) визначена в усіх точках
проміжку (а;b), за винятком, можливо, деякої точки
∈
0
х
(а;b). Побу-
дуємо послідовність значень її аргументу:
1 2 n і 0
х
,
х
,...,
х
, n N,
х х
,
і
1, n
∈ ≠ =
(*)
таку, щоб всі
х
і
у
(а;b) і вона збігалась до точки х
0
:
0n
n
хх
lim =
∞→
.
Тоді значення функції f(х) також утворюють деяку числову пос-
лідовність.
1 2 n
f (
х
), f(
х
),..., f (
х
)
. (**)
Визначення 1. Число А є границею функції f(х) при х, яке прямує
до х
0
, якщо для будь-якої послідовності значень аргументу (*), яка збі-
гається до числа х
0
, послідовність значень функції (**) збігається до
числа A, і записують:
А)х(flim
0
хх
=
→
.
Є й інше, еквівалентне сформульованому вище, означення гра-
ниці функції.
Визначення 2. Число А є границею функції f(x) при x, яке прямує
до х
0
, якщо для будь-якого малого числа
0
>
ε
знайдеться таке мале
число
0
>
δ
, яке залежить від
ε
, що при всіх
)b;а(х
∈
, які задоволь-
няють нерівність
0
| х х |
δ
− <
, виконується нерівність
ε
<
−
|А)х(f|
.
Якщо f(x)=A, коли х→х
0
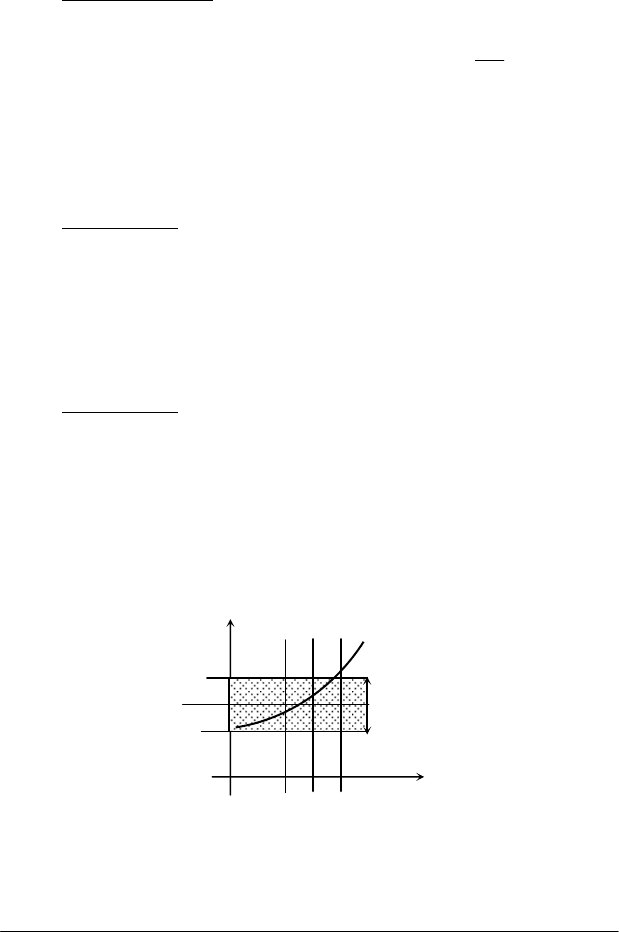
, то на графіку (рис. 2.17) це означає,
що для всіх точок х які лежать від точки х
0
не далі ніж на δ, точки Μ (х,
f(х))
Рис. 2.17
лежать у середині смуги шириною 2ε, межі якої прямі:
ε
−
=
Ау
i
у
А+
ε
А
−
ε
y=f(x)
2
ε
M
0
x
x
0
−
δ
x
0
x
0
+
δ

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
34
ε
+
=
Ау
.
Приклад. Довести, що границя функції
)1х/()1х()х(f
2
+−=
при x, яке прямує до –1, дорівнює –2.
Розв'язання. Доведемо, що для будь-якого числа
0
>
ε
існує чи-
сло
)(
ε
δ
при всіх
1х
−
≠
, які задовольняють нерівність
δ
<
+
|1х|
,
виконується нерівність
ε
<++− |2)1х/()1х(|
2
. (І)
Справді, при
1х
−
≠
маємо:
|1х||21х||2)1х/()1х)(1х(| |2)1х/()1х(|
2
+=+−=+++−=++−
(ІІ)
Якщо взяти
ε
δ
=
, то з нерівності
δ
<
+
|1х|
випливає
ε
<
+
|1х|
, і внаслідок (II) нерівність (І) доведено.
Тобто,
2)1х/()1х(lim
2
1
х
−=+−
−→
.
Сформульовані вище означення границі функції можна узагаль-
нити на випадок, коли замість числа х
0
, береться
+∞
(або
−∞
).
Односторонні границі. Число А є границею функції f(х), де
(
)
0
х а;х
∈
, у точці x
0
ліворуч і записують:
А)х(flim
0
хх
0
=
−→
.
(ІІІ)
Аналогічно, число
А
є границею функції f(x), де
(
)
0
х х ;b
∈
, у
точці
0
х
праворуч і записують:
0
х х 0
lim f (
х ) А
→ +
=
.
(IV)
Ці границі функції звуть односторонніми і вони повинні відпо-
відати визначенню.
Якщо функція визначена на проміжку (а;b), крім, можливо, точ-
ки
)b,a(х
0
∈
, то для існування границі (2.1) необхідно і достатньо,
щоб обидві границі (ІІІ) і (IV) функції f(x) у точці х
0
існували і були
рівними:
=
−→
)х(flim
0
хх
0
А)х(flim
0
хх
0
=
+→
.
У загальному випадку обидві границі функції f(х) у точці х
0
мо-
жуть існувати, але не дорівнювати одна одній.
Наприклад, функція у = arctg(1/x) має область визначення
Rх
0
∈
і
0х
0
≠
. Розглянемо:

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
35
2/)х/1(arctglim
0
х
π
=
+→
,
2/)х/1(arctglim
0
х
π
−=
−→
,
тобто, обидві границі існують, але не дорівнюють одна одній.
Нескінченно малі величини.
Поняття нескінченно малої величини. Числова функція f(x) не-
скінченно мала величина при х, яке прямує до а, якщо виконується
визначення 2, коли
А 0
=
. Тобто,
0)х(flim
ах
=
→
.
Підкреслимо, що нескінченно малу величину треба розуміти як
змінну величину, яка тільки в процесі своєї зміни (коли х прямує до а)
буде менша за довільне наперед дане мале число ε > 0.
Приклад. Величини:
)2/х(сos)х(f
π
+
=
;
2
х)х(f =
;
f(x) = ln(x + 1) нескінченно малі при х, яке прямує до нуля.
Властивості нескінченно малих величин:
- якщо функція у = f(х) має границю b, то вона може бути запи-
сана у вигляді
α
+
=
bу
, де
х а
lim (
х ) 0
α
→
=
α
(х). Правильно й зворотне;
- якщо
α
(х) нескінченно мала величина і не дорівнює нулю при
а
х
→
(або при
∞
→
х
), то
)х(/1у
α
=
нескінченно велика величина;
- алгебраїчна сума двох, трьох і взагалі скінченого числа нескін-
ченно малих величин є нескінченно мала величина;
- добуток нескінченно малої величини на обмежену функцію,
коли х прямує до а (або
∞
→
х
), є нескінченно малою величиною;
- частка від ділення нескінченно малої величини на обмежену
величину, яка має границю відмінну від нуля, коли
а
х
→
(або
∞
→
х
), є нескінченно мала величина.
Усі ці властивості можна подати як теореми і доводити їх. На-
приклад, доведемо останнє твердження.
Нехай
α
(х) - нескінченно мала величина, тобто
0)х(lim
ах
=
→
α
;
z(x) - обмежена функція, тобто
0b)х(zlim
ах
≠=
→
Розглянемо функцію
α
(х)/z(x) коли
а
х
→
. Функцію можна записати так
α
(х)(1/z(x)).
Але
0)х(
→
α
, коли
а
х
→
, а
b/1)х(z/1
→
, тому що
0b
≠
.
Маємо добуток нескінченно малої величини на обмежену величину,
який дає нескінченно малу величину.
Нескінченно великі величини.
Поняття нескінченно великої величини. Функція f(x) нескінчен-
но велика величина при х, яке прямує до а, якщо для будь-якого напе-

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
36
ред даного скільки завгодно великого числа Е > 0 знайдеться таке чис-
ло
0
>
δ
, яке
)Е(
δ
, що для усіх
а
х
≠
, які належать області визначен-
ня функції і задовольняють нерівності
|х а|
δ
− <
, виконується нерів-
ність
Е |)х(f| >
.
Як і у випадку з нескінченно малими, треба зазначити, що жод-
не окремо взяте значення нескінченно великої величини не можна на-
звати як "нескінченно великим" - нескінченно велика величина - це
функція, яка тільки в процесі своєї зміни може стати більшою від дові-
льно взятого числа Е > 0. Тобто
∞=
→
)х(flim
ах
.
Приклад. Величини: f(x) = 1/х при х, яке прямує до нуля;
f(х) = tg(х) при х, яке прямує до
2/
π
є нескінченно великими.
Нескінченно малі й нескінченно великі величини зв'язані між
собою такою залежністю: якщо величина f(х) - нескінченно велика при
а
х
→
, то її обернена величина
)х(f/1)х(
=
α
є нескінченно малою
величиною.
Сформульовані вище означення нескінченно малої та нескін-
ченно великої величин можна узагальнити і на випадок, коли замість
числа а береться
+∞
або
−∞
.
Приклад.
∞=
±∞→
2
х
хlim
. Це нескінченно велика величина;
0хlim
1
х
=
−
±∞→
. Це нескінченно мала величина.
Обмеженість функції. Поняття про обмеженість функції, яка
прямує до границі, розв'язується теоремою.
Теорема. Якщо
b)х(flim
ах
=
→
, при цьому b є скінчена величина,
то функція f(x) є обмеженою.
Доведення. З рівняння
b)х(flim
ах
=
→
, маємо, що
ε
<
−
|b)х(f|
,
якщо
)( |ах|
ε
δ
<
−
. Перепишемо першу нерівність у вигляді
ε
+
<
|b| |)х(f|
. А це і означає, що функція f(х) обмежена при
а
х
→
.
Основні теореми про границі.
Теорема 1. Границя алгебраїчної суми скінченого числа змінних
дорівнює алгебраїчній сумі границь цих змінних:
k
ах
2
ах
1
ах
k21
ах
ulim...ulimulim)u...uu(lim
→→→→
++=+++
.
Доведіть самостійно.

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
37
Теорема 2. Границя добутку скінченого числа змінних дорівнює
добутку границь цих змінних:
k
ах
2
ах
1
ах
k21
ах
ulim...ulimulimu...uulim
→→→→
⋅⋅=
.
Доведіть самостійно.
Висновок. Сталий множник можна виносити за знак границі:
ulimссulim
ахах →→
=
.
Доведіть самостійно.
Теорема 3. Границя частки двох змінних дорівнює частці цих
змінних, якщо границя знаменника не дорівнює нулю:
)vlim/()ulim()v/u(lim
ахахах →→→
=
, якщо
0vlim
ах
≠
→
.
Доведення. Нехай
1
ах
аulim =
→
. Тобто
α
+
=
a
u
,
β
+
=
bv
, де
β
α
,
- нескінченно малі. Напишемо тотожність
=
+
+
=
)b/()а(v\u
β
α
))b(b/()аb(b/а)b/а)b/()а((b/а
β
β
α
β
α
+
−
+
=
−
+
+
+
=
.
Частка а/b є стала величина, а частка
))b(b/()аb(
β
β
α
+
−
є не-
скінченно мала величина. Знаменник
)b(b
β
+
має границею
0b
2
≠
.
Отож,
)vlim/()ulim(b/аv/ulim
ахахах →→→
==
Приклад.
=−+=−+
→→→
))2х4(lim/())5х3(lim()2х4/()5х3(lim
1х1х1х
42/8)214/()513()2хlim4/()5хlim3(
1х1х
==−⋅+⋅=−+=
→→
.
Теорема 4. Якщо між відповідними значеннями трьох функцій
u = и(х), z = z(x), ν = v(x) виконується нерівність
v
z
u
≤
≤
, при цьому
и(х) і ν(x) при
а
х
→
(або при
±∞
→
х
) прямують до однієї границі b,
то z = z(x) при
а
х
→
(або при
±∞
→
х
) прямує до тієї ж границі b.
Доведіть самостійно.
Теорема 5. Якщо при
а
х
→
(або при
∞
→
х
) функція у прий-
має значення
0y
≥
і при цьому прямує до границі b, то
0b ≥
.
Доведіть самостійно.
Теорема 6. Якщо між відповідними значеннями двох функцій
u = и(х) і ν = ν(x), які прямують до границь при
а
х
→
(або при
∞
→
х
), виконується нерівність
uv
≥
, то має місце нерівність
0ulimvlim
ахах
≥≥
→→
.
Доведіть самостійно.

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
38
Приклад. Довести, що
0xsinlim
0х
=
→
.
Розв'язання. Розглянемо сектор АОВ одиничного кола
(рис.2.18). Якщо: ОА = 1, х > 0, то відрізок АС = sinx, дуга
хАВ =
∪
, sinx
< х. Очевидно, що при х < 0 буде |sinx|<|x|. З цих нерівностей та тео-
рем 5 і 6 прямує, що
0xsinlim
0х
=
→
.
Теорема 7. Якщо змінна величина ν зростаюча, тобто будь-яке її
наступне значення більше від попереднього, і якщо вона обмежена
(v < М), то ця змінна величина має границю
Avlim
ах
=
→
, яка не переви-
щує
М
.
Доведіть самостійно.
Приклад. Довести, що
1xcoslim
0х
=
→
.
Розв'язання. Змінна величина
cos x
обмежена зверху одиницею.
З тригонометричних тотожностей маємо:
)2/x(sin21xcos
2
−=
, тоб-
то
))2/x(sin21(limxcoslim
2
0х0х
−=
→→
, але
|xsin| |)2/xsin(| <
і тому
0)2/xsin(lim
0х
=
→
. Таким чином
101))2/xsin(lim(21))2/x(sin21(lim
2
0х
2
0х
=−=−=−
→→
.
Отже,
х
0
limcos x 1
→
=
.
ЛЕКЦІЯ № 7
Деякі важливі границі. У теорії границь важливе місце займають
подані нижче границі, за допомогою яких обчислюють багато границь
від елементарних функцій:
1х/)x(sinlim
0х
=
→
;
е)x1(lim
х/1
0х
=+
→
;
е)x/11(lim
х
х
=+
∞→
;
alnх/)1а(lim
х
0х
=−
→
;
1х/)1е(lim
х
0х
=−
→
;
aln/1х/))х1((loglim
а
0х
=+
→
;
х
0
lim(ln(1
х ))/ х 1
→
+ =
.
Тут введено число
...71828,2е
=
, яке є ірраціональним.
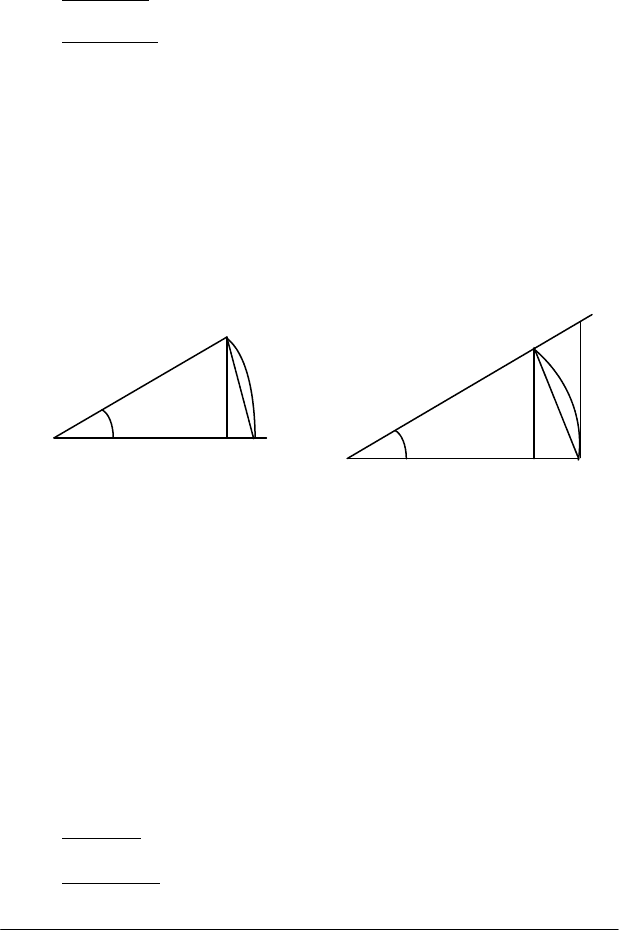
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
39
Теорема 1.
1)х/x(sinlim
0х
=
→
.
Доведення. Функція у = sinx/x не визначена при х = 0, тому що
чисельник та знаменник дробу перетворюються у нуль. Знайдемо
границю цієї функції коли
0х
→
. Розглянемо сектор
АОМ
кола, раді-
ус якого ОА = ОМ = 1; центральний кут ∠МОА = x =
∪
МА
, нехай
2/х0
π
<
<
(рис.2.19). Відносно площин безпосередньо маємо:
S
∆MOA
< S
сектора МOA
< S
∆ОАС
.
Обчислимо кожну з цих площин:
MOA
S (1/2)
ОА МВ (1/2)1sinx (1/2)sinх
∆
= = =
;
S
сектора МОА
2
(1/2)
ОА МА (1/2)1x (1/2)х
= = = ;
OA
С
S (1/2)
ОА АС (1/2)1tgx (1/2)tgх
∆
= = =
.
Рис. 2.18 Рис. 2.19
Ці величини підставимо у нерівність. Після скорочення на 1/2,
маємо: sinx < х < tgx. Розділимо усі члени нерівності на sinx;
1 < x/sinx < 1/cosx, або 1 > sinx/x > cosx.
Останні нерівності виведені з умови, що х > 0, але функції:
sin(–х)/(–х) = sinx/x і cos(–x) = cosx парні, тобто нерівність правильна,
коли х < 0.
Раніше було доведено, що
1xcoslim
0x
=
→
, а
11lim
0x
=
→
.
Отже, змінна sinx/x розташована між двома величинами, які ма-
ють одну й ту ж границю, яка дорівнює 1; таким чином, за теоремою 4
(попередня лекція), маємо
1)х/x(sinlim
0x
=
→
.
Приклад. Знайти границю
)х2/()xcos1(lim
2
0x
−
→
.
Розв'язання
.
2 2 2 2
x 0 x 0
lim( 2sin ( x / 2))/( 2
х ) lim sin ( x / 2 )/(2х / 2 )
→ →
=
M
B
C
0
x
A
A
B
C
0
