Станішевський С.О. Вища математика. Конспект лекцій. Модуль 1
Подождите немного. Документ загружается.


Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
50
)хх()х(fуу
000
−⋅
′
=−
. (2.9)
Приклад. Знайти тангенс кута нахилу дотичної до графіку фун-
кції
2
ху =
у точці M(1/2, 1/4).
Розв'язання. Візьмемо похідну від функції
2
ху =
.
х2у =
′
;
0 0
tg
у ( х ) 2(1/ 2) 1
α
′
= = =
. Відкіля
0
α
= 45°.
Загальні правила здобуття похідної. Нехай маємо деякі функції
)х(uu
=
,
(
х )
υ υ
=
, які диференційовані у проміжку (а,b). Тоді:
- якщо
сu
у
=
, то
uс)сu(у
′
=
′
=
′
, (2.10)
де с – const, тобто сталий множник можна виносити з-під знаку похід-
ної;
- якщо
у u
υ
= ±
, то
у (u ) u '
υ υ
′ ′ ′
= ± = ±
(2.11)
тобто похідна суми або рівниці функцій дорівнює сумі або різниці їх-
ніх похідних;
- якщо
у u
υ
=
, то
у (u ) u 'u
υ υ υ
′ ′ ′
= = +
, (2.12)
тобто похідна добутку двох функцій дорівнює сумі добутків похідної
першої функції на другу функцію і похідної другої функції на першу
функцію;
- якщо
у u /
υ
=
, то
2
у (u / ) (u ' u )/
υ υ υ υ
′ ′ ′
= = −
, (2.13)
тобто похідна частки двох функцій дорівнює дробу, у якому знамен-
ник є квадрат знаменника, а чисельник є різниця між добутками похід-
ної чисельника на знаменник і добутком похідної знаменника на чисе-
льник дробу;
- якщо функція у = f(x) має похідну у деякій точці
)b;а(х
∈
, а
функція z = F(y) має похідну у відповідній точці у = f(x), то й складна
функція z = F(f(x)) май похідну у точці х, причому
)х(f))х(f(F))х(f(F(z
x
'
у
′
⋅=
′
=
′
, (2.14)
де індекси у і x біля похідних кажуть, за яким аргументом обчислюють
похідні;
- якщо функція у = f(х) задовольняє умові існування оберненої
функції і у точці
)b;а(х
∈
має скінчену і відмінну від нуля похідну, то
обернена функція х = f
–1
(у) у відповідній точці у = f(х ) також має похі-
дну. Похідні цих взаємно обернених функцій зв'язані рівністю
)х(f/1))у(f(
'
х
'
у
1
=
−
. (2.15)
Кожне з цих правил можна розглядати як теорему.
Доведемо,
наприклад, правило (2.13). Тут: у = u/
υ
; ∆y, ∆u i ∆
υ
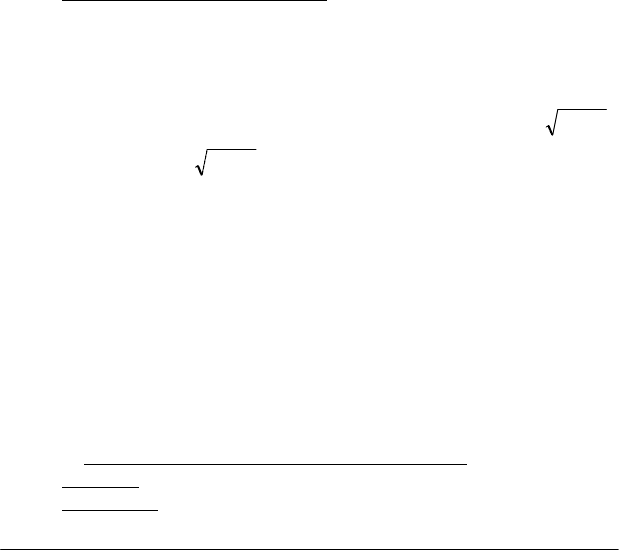
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
51
є прирости функцій у(х), и(х),
υ
(x), відповідні приросту ∆x аргументу
х.
Тоді
у у (u u )/( ),
∆ ∆ υ ∆υ
+ = + +
у (u u ) /( ) u / ,
∆ ∆ υ ∆υ υ
= + + − =
( u u )/( ( ))
υ∆ ∆υ υ υ ∆υ
= − +
.
Останню рівність розділимо на ∆x:
у / х ( u u )/( х ( ))
∆ ∆ υ∆ ∆υ ∆ υ υ ∆υ
= − ⋅ + =
( u /
х u / х )/( ( )).
υ∆ ∆ ∆υ ∆ υ υ ∆υ
= − +
Знайдемо границю цього співвідношення. Маємо:
х
0
х
0
х
0
у lim у / х lim ( u / х u / х )/ lim ( ( ))
∆ ∆ ∆
∆ ∆ υ∆ ∆ ∆υ ∆ υ υ ∆υ
→ → →
′
= = − + =
2
х
0
х
0
х
0
( lim u /
х u lim / х )/( lim ).
∆ ∆ ∆
υ ∆ ∆ ∆υ ∆ υ υ ∆υ
→ → →
= − +
Так як ν(x) - диференційована і, отже, неперервна функція, то
х
0
lim 0
∆
∆υ
→
=
. Маємо
2
у ( u u ')/
υ υ υ
′ ′
= −
, де
0
υ
≠
,
що і треба було довести.
Похідні елементарних функцій.
Якщо у = const, то у' = 0.
Степенева функція; у = u
α
,
1
у u u
a
a
-
ў ў
= Ч
, де u=u(x).
Тригонометричні функції: у = sinx, y' = cosx; у = cosx, y' = –sinx; у =
tgx, y' = 1/cos
2
x; у = ctgx, y' = –1/sin
2
x.
Обернені тригонометричні функції:
xarcsinу
=
,
2
х1/1у −=
′
;
x
arccos
у
=
,
2
х1/1у −−=
′
;
arctgx
у
=
,
)х1/(1у
2
+=
′
;
arcсtgx
у
=
,
)х1/(1у
2
+−=
′
.
Показникова функція:
х
ау =
,
alnау
х
=
′
; якщо у = e
x
,
х
еу =
′
.
Логарифмічна функція:
хlogу
а
=
,
)alnх/(1у =
′
; якщо
хlnу
=
,
х/1у =
′
.
Гіперболічні функції:
shxу
=
,
сhxу =
′
;
сhxу
=
,
shxу =
′
;
thxу
=
,
xсh/1у
2
=
′
;
сthxу
=
,
xsh/1у
2
−=
′
.
Показниково-степенева функція:
у u
υ
=
, (де
u(
х ), (х))
υ
;
1
у u u u 'lnu
υ υ
υ υ
−
′ ′
= ⋅ +
. (2.16)
Доведення деяких формул диференціювання.
Теорема.
Похідна від sinx є cosx.
Доведення.
Дамо аргументу х приріст
х
∆
;

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
52
тоді:
)ххsin(уу
∆
∆
+
=
+
,
де у = sіnx.
=
+
+
⋅
−
+
=
−
+
=
)2/)хххcos(()2/)хххsin((2хsin)ххsin(у
∆
∆
∆
∆
)2/ххcos()2/х(хsin2
∆
∆
+
⋅
=
; розділимо на
х
∆
.
х/))2/ххcos()2/х(хsin2(х/у
∆
∆
∆
∆
∆
+
⋅
=
.
Знайдемо границю:
)2/ххcos(lim)2/х/()2/х(sin(limх/уlimу
0х0х0х
∆∆∆∆∆
∆∆∆
+==
′
→→→
,
але
1))2/х/()2/х(sin(lim
0х
=
→
∆∆
∆
, тому
xcos)2/ххcos(limу
0х
=+=
′
→
∆
∆
.
Остання рівність має місце тому, що функція cosx є непере-
рвною у області свого визначення.
Теорема. Похідна від tgx є
хcos/1
2
.
Доведення. Функція у = tgx може бути записана у вигляді дробу:
у = sinx/cosx, за правилом (2.13), маємо:
x.1/cosxx)/cossinx(cosxcos/)хsin)(cosx-cosx)x((sinу
22222
=+=
′′
=
′
Теорема. Похідна від функції
хlog
а
дорівнює
)alnх/(1
⋅
.
Доведення. Якщо
у
∆
є приріст функції
хlogу
а
=
, який відпо-
відає приросту
х
∆
аргументу х, то
);хх(logуу
а
∆∆
+=+
хlog)хх(logу
аа
−+=
∆∆
; після потенціювання
)х/х1(logу
а
∆∆
+=
.
Поділимо обидві частини останньої рівності на
х
∆
:
)х/х1(log)х/1(х/у
а
∆∆∆∆
+=
.
Помножимо і поділимо на х вираз, який стоїть праворуч у останній
рівності:
х/х
аа
)х/х1(log)х/1()х/х1(log)х/х)(х/1(х/у
∆
∆∆∆∆∆
+=+=
.
Вираз, який стоїть під знаком логарифму, має границю е, коли
0х
→
∆
. Виконавши граничний перехід з обох сторін, маємо:
х
/
х
а а
х
0
х
0
у lim у / х lim (1/ х )log (1 х / х ) (1/ х )log
∆
∆ ∆
∆ ∆ ∆
→ →
′
= = + = ×
х
/
х
а
х
0
lim (1
х / х ) (1/ х )log е 1/( х lna )
∆
∆
∆
→
× + = = ⋅
.
Отже, теорему доведено.
Теорема. Похідна від функції
α
ху =
, де
R
∈
α
, дорівнює
1
x
−
α
α
.
Доведення. Нехай х > 0. Логарифмуємо дану функцію, маємо
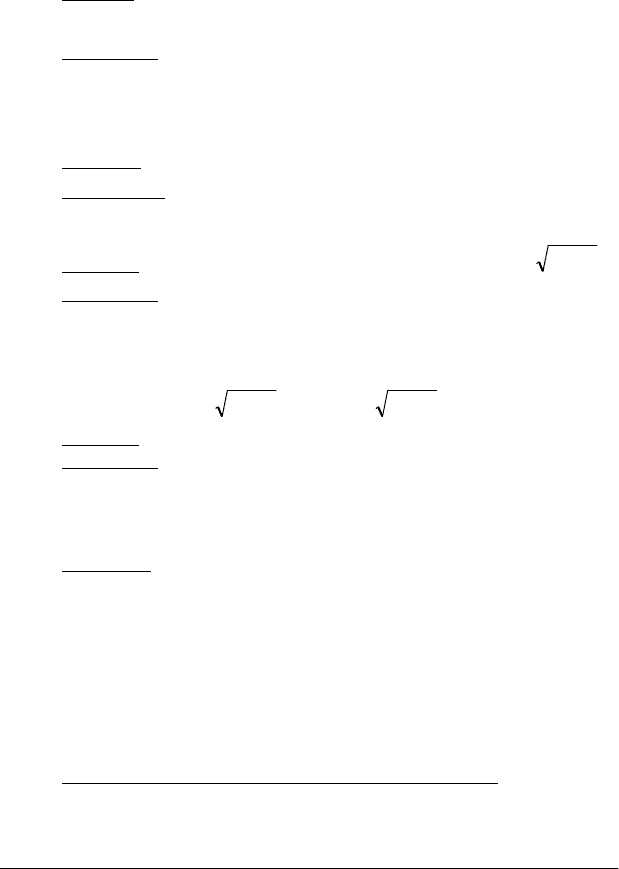
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
53
xlnyln
α
=
. Візьмемо похідну від обох частин рівності:
x/у/y
α
=
′
. Звідси
1
x)x/(x)x/(yy
−
===
′
αα
ααα
.
Теорема. Похідна від показниково-степеневої функції
(
х
)
у u( х )
υ
=
дорівнює
u ( 'lnu u / u )
υ
υ υ
′
+
.
Доведення. Логарифмуємо дану функцію:
ln y lnu
υ
=
.
Візьмемо похідну від обох частин рівності:
y /
у 'lnu u / u
υ υ
′ ′
= + ⋅
.
Відкіля
y u ( ' lnu u / u )
υ
υ υ
′ ′
= +
. Це формула (2.16).
Приклад. Знайти похідну від функції
х
ху =
.
Розв'язання.
xlnxyln
=
;
)х/1(xxlnу/у +=
′
;
)1x(lnуу +=
′
;
)1x(lnху
х
+=
′
.
Теорема. Похідна від функції
xarcsinу
=
дорівнює
2
х1/1 −
.
Доведення. Оберненою функцією до функції
xarcsinу
=
є фун-
кція х = siny. За теоремою про похідну оберненої функції (формула
2.15) маємо:
))xin/(cos(arcs1ycos/1)у/(sin1)x(arcsin ==
′
=
′
.
Оскільки
2
х1)xcos(arcsin −=
, то
2
х1/1у −=
′
.
Теорема. Похідна від гіперболічної функції shx дорівнює chx.
Доведення. За визначенням гіперболічних функцій:
2/)ее(shx
хх
−
−=
;
2/)ее(сhx
хх
−
+=
.
(
)
'
ах
е
=
ах
ае
. Маємо
chx2/)ее()2/)ее(()shx(
хххх
=+=
′
−=
′
−−
.
Приклади. Знайти похідні:
x3sinху
2
=
;
=
′
+
′
=
′
)x3(sinхx3sin)х(у
22
2
2
х sin3x 3х cos3x
+
;
x2cos/ху
3
=
;
=
′
−
′
=
′
x2cos/)х)x2(cosx2cos)х((у
233
x2cos/)x2sinх2x2cos3(хx2cos/)х)x2sin2(x2cosх3(
22232
+=+=
.
ЛЕКЦІЯ № 10
Похідна функції, заданої у параметричній формі. Нехай функ-
цію задано у параметричній формі:
)t(у
ψ
=
,
)t(х
ϕ
=
, де t – параметр. (2.17)

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
54
Функції
)t(
ψ
і
)t(
ϕ
- неперервні і диференційовані, коли
);(t
β
α
∈
. Нехай у деякій точці
);(t
0
βα
∈
існує додатна похідна
)t(х
0tt
ϕ
′
=
′
, тоді вона додатна і у деякому околі
0
t
і, отже, у цьому
околі функція
)t(
ϕ
монотонно зростаюча. З попереднього відомо, що
неперервна і монотонно зростаюча функція має обернену функцію t =
t(x), їх похідні зв'язані рівністю
xt
t/1х
′
=
′
. (2.18)
Підставивши t = t(x) у другу з рівностей (2.17), дістанемо явну
форму завдання функції (2.17) на деякому проміжку значень х:
)х(f))х(t(у
=
=
ψ
.
її похідну, як похідну складної функції, обчислюємо за формулою
хtх
tу
′
⋅
′
=
′
ψ
.
За формулою (2.18) цю похідну запишемо у вигляді:
ttх
х/у)t(/)t(у
′
′
=
′
′
=
′
ϕψ
або
)dt/dх/()dt/dy(dx/dy
=
. (2.19)
Знайдений вираз для першої похідної функції, заданої в параме-
тричному вигляді, дає можливість обчислити тангенс кута нахилу до-
тичної до її графіка:
tt
х/уtg
′
′
=
α
, (2.20)
а також написати рівняння дотичної до графіка функції (2.17) у заданій
точці, коли
0
tt =
.
Приклад. Знайти кут нахилу дотичної до графіка функції:
t
cos
а
х
=
,
tsinау
=
, де
π
≤
≤
t0
, у точці, яка відповідає
4/t
π
=
.
Розв'язання.
ctgt)tsinа/()tcosа()tcosа/()tsinа(у
ttх
−==
′
′
=
′
;
1)4/(ctgtg
−
=
−
=
π
α
; відкіля
4
3
135
0
π
α
==
.
Похідні вищого порядку. Нехай функція f(х) диференційована у
проміжку (а;b). Похідна цієї функції f'(x) є функцією аргументу x. Ві-
зьмемо деяку точку
)b;а(х
0
∈
; дамо приріст аргументу
0
ххх −=
∆
, і
матимемо приріст функції f'(x) у точці х
0
:
)х(f)хх(f)х(f
000
′
−+
′
=
′
∆∆
.
Розглянемо границю
)х(fх/)х(flim
00
0
х
′
′
=
′
→
∆∆
∆
.
Якщо ця границя існує, то кажуть, що функція f(х) має похідну другого
порядку (або другу похідну) у точці х
0
і
ЇЇ
позначають:
)х(fу
0
′
′
=
′
′
, або
2
0
2
dx/)х(fd
, або
0
хх
)х(f
=
′′
.

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
55
Аналогічно визначають похідні третього, четвертого і наступ-
них порядків.
Складніше обчислити другу похідну функції, заданої у парамет-
ричній формі:
ххtххtххtхххх
)t(t)()t()у(у
′
′
′
+
′
⋅
′
′
=
′
′
⋅
′
=
′
′
=
′
′
ψψψ
.
Обчисливши похідну по х від функції
t
ψ
′
як похідну складної
функції:
хttхt
t)(
′
⋅
′
′
=
′
′
ψψ
, дістанемо
ххt
2
хtttt
t)t(у
′′
⋅
′
+
′′′
=
′′
ψψ
. Оскільки
tх
х/1t
′
=
′
, то
3
tttхtt
2
tхtхххх
)х/(хtх))х/(1()х/1()t(t
′′′
−=
′
⋅
′′
⋅
′
−=
′′
=
′′
=
′′
.
Остаточно маємо:
3
ttttttttt
)х/()хуху(у
′′′
⋅
′
−
′
⋅
′′
=
′′
. (2.21)
Приклад. Знайти
у
′
′
′
, якщо у = sin
3
х.
Розв'язання. Послідовно знайдемо у', у",
у
′
′
′
:
xcosxsin3у
2
=
′
;
=
′
=
′′
)xcosxsin3(у
2
2 2 3
3sin x(2cos x sin
х ) 6 sin x 9 sin х
− = −
.
)хsin92(xcos3xcosхsin27xcos6)xsin9xsin6(у
223
−=−=
′
−=
′′′
.
Приклад. Знайти
xx
y
′
′
, якщо
t
cos
а
х
=
,
tsinbу
=
.
Розв'язання. Знайдемо
xx
y
′
′
за формулою (2.21). Для цього обчи-
слимо перші і другі похідні від даних функцій по змінній t:
tsinах
t
−=
′
,
tcosах
tt
−=
′
′
;
tcosbу
t
=
′
,
tsinbу
tt
−=
′
′
.
2 2 3
d y / dx (( а sint )( b sint ) (bcost )( а cost ))/( а si
nt )
= − − − − −
)tsinа/(b
32
−=
.
Диференціал. Визначення. Нехай у = f(х) функція, де
х
∈
(а;b),
неперервна у деякій тичці x
0
(
а;b)
∈
і приросту аргументу
х
∆
відпові-
дає приріст функції:
)х(f)хх(f)х(fу
000
−+==
∆∆∆
, який є функці-
єю аргументу
х
∆
.
Якщо для приросту функції
у
∆
існує таке число
0А
≠
, що при-
ріст функції можна записати у вигляді:
у А х ( х ) х
∆ ∆ ε ∆ ∆
= ⋅ + ⋅
, де до-
даток
)х(
∆
ε
задовольняє рівності:
0х/)х(lim
0х
=
→
∆∆ε
∆
, то кажуть, що
дана функція диференційована у точці х
0
.
Вираз
хА
∆
⋅
є диференціалом функції у = f(x) у точці х
0
, його
позначають dy або
)х(df
0
. Отже, диференціал - це лінійна частина
приросту функції.
Зв'язок між диференційованістю функції та існуванням її похід-
ної встановлюють за теоремою.

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
56
Теорема. Щоб функція у = f(х) у точці х
0
була диференційована,
необхідно і достатньо, щоб вона мала у цій точці скінчену похідну
)х(f
0
′
. Якщо виконується ця умова, то f'(х
0
) = А і
х)х(fdу
0
∆
′
=
.
Тут
х
∆
не обов'язково нескінченно мала; але якщо
х
∆
- нескін-
ченно мала, то й dy - нескінченно мала і саме у цих випадках dy (за
умови, що
0)х(f
0
≠
′
) є головною частиною нескінченно малого при-
росту функції
у
∆
.
Диференціалом незалежної змінної х у точці х
0
звуть її приріст
х
∆
,
тобто
хdx
∆
=
.
З урахуванням цієї рівності, маємо:
dx)х(fdу
′
=
. (2.22)
Отже:
dx/dy)х(f =
′
, (2.23)
тобто похідна дорівнює відношенню диференціалів функції та аргуме-
нту.
Правила обчислення диференціалів. Правила обчислення дифе-
ренціалів суми, різниці, добутку і частки двох функцій аналогічні від-
повідним правилам обчислення похідних:
d(cf(x)) = c(df(x)), де с - стала;
d(f(x) ± g(x)) = df(x) ± dg (x);
d(f(x)
· g(x)) = g(x) df(х) + f(x)dg(x);
d(f(x)/g(x)) = (g(x)·df(x) – f(х) dg(x))/g
2
(x).
Приклад. Знайти диференціал функції у = x
2
/sinx.
Розв'язання.
=−= xsin/))x(sindх)х(xd(sin)xsin/х(d
2222
xsin/dx)xcosxxsinх2(
22
−=
.
Геометрична інтерпретація диференціала. Нехай у = f(х) - деяка
функція, Μ (х
0
; f(х
0
))- точка, яка належить графіку функції. Проведемо
через точку Μ дотичну до графіка функції. Кутовий коефіцієнт нахилу
дотичної (тангенс кута нахилу) дорівнює значенню похідної
)х(f
0
′
.
Якщо аргументу функції надати приріст
х
∆
,
то приріст функції
у
∆
дорівнюватиме:
)х(f)хх(fу
00
−+=
∆∆
.
На рис. 2.27 приріст ординати функції
у
∆
дорівнює довжині ві-
дрізка М
1
Р.
При тому самому прирості аргументу
х
∆
приріст дотичної до-
рівнюватиме довжині відрізка ΝΡ. Обчисливши |ΝΡ| як катет прямоку-
тного трикутника МNР, знаходимо:
0
| NP| |
МP|tg f (х ) х
α ∆
′
= =
.
За
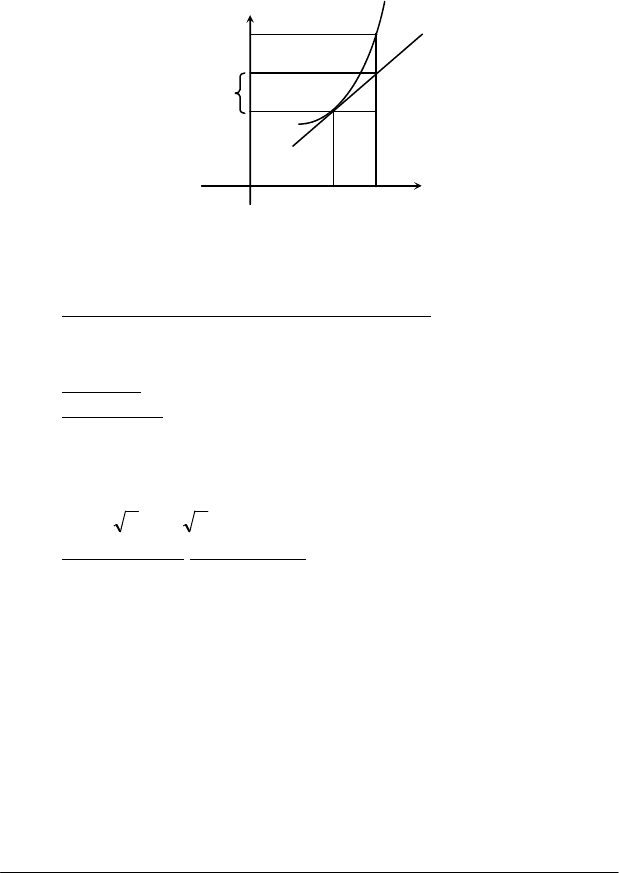
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
57
означенням
dyх)(хf
0
=
′
∆
, отже |NP| = dy. Таким чином, dy є прирос-
том ординати дотичної.
Рис. 2.27
Диференціал у наближених обчисленнях. Формули приросту
функції записуємо у вигляді:
)f(хх)(хfх)f(х
000
+
′
≈+
∆∆
. (2.24)
Приклад. Обчислити sin46
0
.
Розв’язання. Покладемо
4/х
0
π
=
, що відповідає 45
0
;
180/х
π
∆
=
, що відповідає 1
0
;
180/4/хх
π
π
∆
+
=
+
. Підставивши ці
величини у (2.24), будемо мати:
)4/cos()180/sin()4/sin()180/4/sin(46sin
0
πππππ
⋅+≈+=
;
7191,00175,07071,07071,0180/2/22/246sin
0
≈⋅+≈⋅+≈
π
.
Інваріантність диференціала. Нехай у = f(x) і х = g(t) - деякі фун-
кції зазначених аргументів такі, що з них можна утворити складну фу-
нкцію
))t(g(fу
=
.
Диференціал функції у = f(x) в припущенні, що х - незалежна
змінна, визначається рівністю
dх)x(fdy
′
=
.
Якщо розглядати функцію у як функцію незалежної змінної t, то
її диференціал визначається рівністю
dtydy
t
⋅
′
=
.
Підставивши в цю рівність замість похідної
t
у
′
її вираз через
х
f
′
і
t
g
′
, за формулою похідної складної функції, дістанемо
dtgfdy
t
х
⋅
′
⋅
′
=
. (2.25)
Але, з іншого боку,
dxdgdtg
t
==
′
; отже, рівність (2.25) запи-
у
0
х
f(x
0
+∆x)
f(x
0
)
N
P
M
x
0
+∆x
x
0
M
1
dу
y=f(x)

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
58
шемо у вигляді
dхfdy
х
⋅
′
=
.
Таким чином, припустивши, що у є функція аргументу t, ми діс-
тали той самий вираз для диференціала dy, як і тоді, коли припускали,
що у є функція аргументу х, тобто форма диференціала не залежить від
того, чи є функція х незалежною змінною, чи вона в свою чергу є фун-
кцією якоїсь змінної. Це і є інваріантність диференціала.
Диференціали вищих порядків. Вище введено перший диферен-
ціал:
dх)х(fdy ⋅
′
=
. Він є функцією х, але від x може залежати тільки
перший множник
)х(f
′
, другий множник dх є приріст незалежної
змінної х і від значення цієї змінної не залежить. Оскільки dy є функція
від х, то маємо право говорити про диференціал цієї функції.
Диференціал від диференціала функції називають другим дифе-
ренціалом або диференціалом другого порядку і позначають:
22
)dx)(х(fdx)dx)х(f()dx)х(f(d)dy(dyd
′′
=
′′
=
′
==
.
Прийнято, коли записуємо степінь диференціала, дужки не пи-
сати. Тобто, замість (dx)
2
пишемо dx
2
.
Третім диференціалом або диференціалом третього порядку
функції зветься диференціал від її другого диференціала і так далі.
ЛЕКЦІЯ № 11
Основні теореми диференціального числення.
Теорема 1. Про корені похідної або теорема Ролля. Якщо функ-
ція f(x) неперервна на відрізку [а;b], диференційована в усіх внутріш-
ніх точках цього відрізку і f(а) = f(b), то знайдеться хоча б одна точка
х = с, де а < с < b, в якій
0)с(f =
′
.
Доведення. Оскільки функція f(x) неперервна на [а,b], то вона
має на ньому найбільше значення Μ і найменше значення т.
Якщо
Μ = т, то функція стала. Похідна від сталої величини до-
рівнює нулю і теорема доведена.
Нехай f(c) = Μ, де а < с < b. Через те, що f(с) - найбільше зна-
чення функції, то f(с +
∆
x) – f(с)
0
≤
як при
0х
>
∆
, так і при
0х
<
∆
.
Отже:
0х/))с(f)хс(f(
≤
−
+
∆
∆
, коли
0х
>
∆
,
0х/))с(f)хс(f(
≥
−
+
∆
∆
, коли
0х
<
∆
.
Оскільки за умовою теореми f(с) існує, тобто,
)с(fх/))с(f)хс(f(lim
0
х
′
=−+
→
∆∆
∆
. Але тут
0)с(f ≤
′
, коли
0х
>
∆
і
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
59
0)с(f ≥
′
, коли
0х
<
∆
. Ці співвідношення сумісні лише тоді, коли
f (
с )
′
= 0. Отже, між а і b є точка с, де похідна дорівнює нулю.
Теорема доведена повністю. Геометрично це означає, що дотич-
на до графіка функції у точці с паралельна вісі абсцис.
Теорема 2. Про скінченні прирости функції або теорема Лагра-
нжа. Якщо функція f(х) неперервна і диференційована на відрізку [а;b],
то знайдеться хоча б одна точка с, де а < с < b, в якій
)ab)(с(f)а(f)b(f −
′
=−
.
Доведення. Визначимо число Q рівністю
Q)ab/())а(f)b(f( =−−
. Складемо допоміжну функцію
F(
х ) f ( х ) f (а ) ( х а )Q
= − − −
. Очевидно, що
0)а(F
=
і
0)b(F
=
.
Функція F(x) неперервна на відрізку [a,b] і диференційована у кожній
внутрішній точці. Отже, вона відповідає теоремі Ролля, за якою усере-
дині відрізка є точка с така, що
0)с(F =
′
. Але
Q)х(f)х(F −
′
=
′
.
Отже,
0Q)с(f)с(F =−
′
=
′
, відкіля
Q)с(f =
′
, тобто
)ab)(с(f)а(f)b(f −
′
=−
, що і треба було довести.
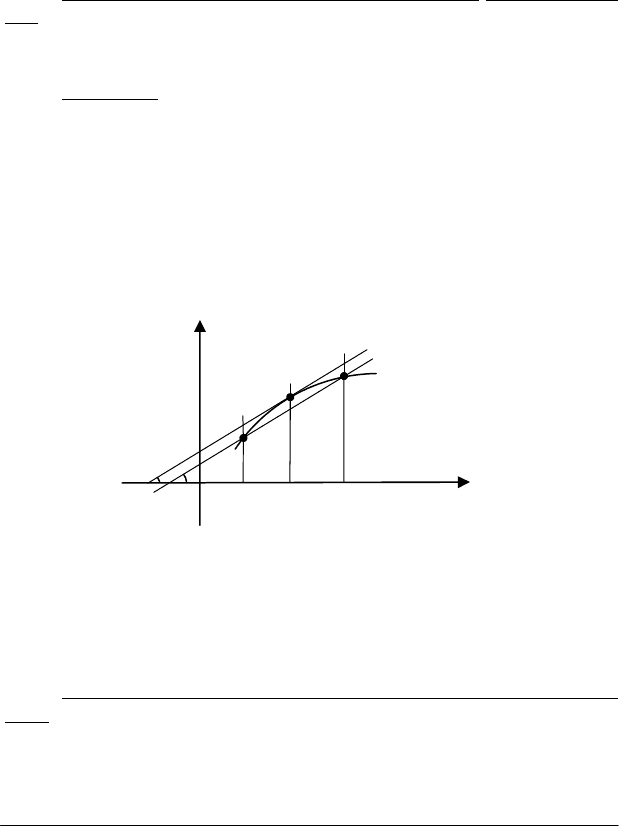
Рис. 2.28
Геометрично це означає, що на дузі графіка функції у = f(x)
знайдеться точка С між А і В, у якій дотична паралельна хорді, яка
з'єднує точки А і В (рис. 2.28).
Теорема 3. Про відношення приросту двох функцій або теорема
Коші. Якщо f(х) і
ϕ
(х) - дві функції, неперервні і диференційовані на
відрізку [а,b], причому
(
х ) 0
ϕ
′
≠
, то знайдеться така точка х = с, а < с
< b, що матиме місце рівність:
)с(/)с(f))a()b(/())а(f)b(f(
ϕϕϕ
′
′
=−−
.
α
α
у
у=f(х)
В
А
0
с
b
