Станішевський С.О. Вища математика. Конспект лекцій. Модуль 1
Подождите немного. Документ загружается.


Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
40
2 2 2 2
x 0
(1/ 2) lim(sin( x/ 2 ))/(
х / 2)) (1/ 2) 1 1/ 4
→
= = ⋅ =
Число е. Розглянемо змінну величину
n
)n/11( +
, де n - зроста-
юча змінна величина, яка має значення 1,2, 3, ...
Теорема 2. Змінна величина
n
)n/11( +
при
∞
→
n
має границю,
яка розташована між 2 і 3.
Доведення. Запишемо формулу бінома Ньютона:
+⋅−++=+
2n
)n/1)(21/())1n(n()n/1)(1/n(1)n/11(
n3
)n/1(...)n/1)(321/())2n)(1n(n( ++⋅⋅−−
.
Перетворимо частину, яка розташована праворуч:
++−−⋅⋅+−⋅++=+ ...)n/21)(n/11)(321/(1)n/11)(21/(111)n/11(
n
)n/)1n(1)...(n/21)(n/11)(n...321/(1
−
−
−
−
⋅
⋅
+
.
Остання рівність вказує на те, що величина
n
)n/11( +
- зростаюча
змінна величина при зростаючому n. Покажемо, що вона обмежена.
Замінимо одиницею кожний вираз вигляду:
)n/11(
−
,
)n/21(
−
…,
матимемо:
)n...321/(1...)321/(1)21/(111)n/11(
n
⋅⋅++⋅⋅+⋅++<+
,
перетворимо кожний добуток у знаменнику у степінь двійки і запише-
мо:
+<+ 1)n/11(
n 1n2
2/1...2/12/11
−
++++
.
Підкреслені праворуч елементи нерівності утворюють геометричну
прогресію із знаменником 1/2 і першим членом 1, тому
3)2/1(21)2/11/())2/1(1(1)n/11(
1nnn
<−+=−−+<+
−
.
Якщо n = 1 маємо ліворуч 2. Тобто,
3)n/11(2
n
<+≤
, що й треба бу-
ло довести.
Таким чином, розглянута змінна величина зростаюча і обме-
жена, тому за теоремою 7 (попереднього розділу) вона має грани-
цю. Цю границю позначають буквою е:
е)n/11(lim
n
n
=+
∞→
.
Теорема 3. Функція у = (1 + 1/х)
х
, коли
±∞
→
х
, прямує до гра-
ниці, яка дорівнює е:
е)х/11(lim
х
х
=+
±∞→
.
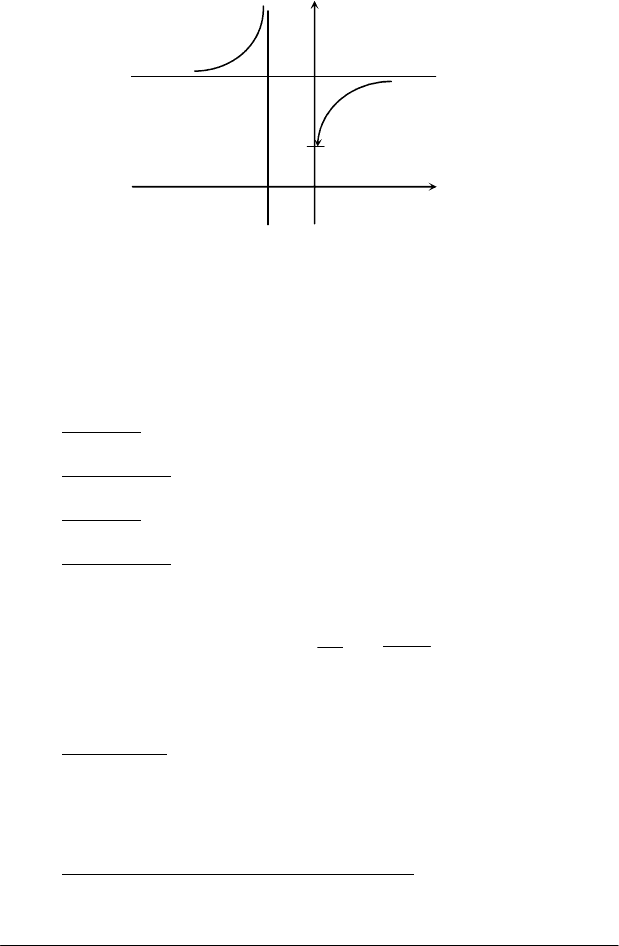
Доводити цю теорему не будемо, а розглянемо її графік
(рис.2.20). Функція визначена, коли
x ( ; 1) (0; )
∈ −∞ − ∪ ∞
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
41
Рис. 2.20
Бачимо, що
е)х/11(lim
х
х
=+
±∞→
. Якщо зробити заміну 1/х = α, то
коли
∞
→
х
, маємо:
0
→
α
(але
0
≠
α
) і можемо записати:
е)1(lim
/1
0
=+
→
α
α
α
.
Приклад. Обчислити границю:
х
х
)х/21(lim +
∞→
.
Розв'язання.
222/х
х
х
х
е))х/21(lim()х/21(lim =+=+
∞→∞→
.
Приклад. Обчислити границю:
3х
х
))1х/()3х((lim
+
∞→
−+
.
Розв'язання.
=−+
+
∞→
3х
х
))1х/()3х((lim
=−+=−−++=
+
∞→
+
∞→
3х
х
3х
х
))1х/(41(lim)1)1х/()3х(1(lim
.
4
1х
4)3х(
lim
4
1х
х
е))1х/(41(lim(
х
=−+=
−
+
−
∞→
∞→
,
де
4)1х/()4)3х((lim
х
=−⋅+
∞→
.
Зауваження. Функція
х
еу =
має назву експонента. Вона відіграє
дуже велику роль у технічних науках. Функція у = lnx має назву лога-
рифма натурального. У його основі лежить число е. Між логарифмом
десятковим і логарифмом натуральним є зв'язок:
lgx = lnx/ln10, або lпх = 2,302585 lgx.
Порівняння нескінченно малих величин.
Нехай одночасно декі-
лька нескінченно малих величин
)х(
α
,
)х(
β
,
)х(
γ
прямують до ну-
у
е
х
1
–1
0

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
42
ля, коли
а
х
→
(або
±∞
→
х
). Розглянемо їх відношення (при цьому
мають на увазі, що величина, яка стоїть у знаменнику дробу, відмінна
від нуля принаймні для значень х, досить близьких до числа а).
Будемо далі користуватися такими визначеннями:
Визначення 1. Якщо
А/lim
ах
=
→
αβ
, причому
0
≠
Α
і
1
А
≠
, то
нескінченно малі
)х(
α
і
)х(
β
одного порядку мализни.
Приклад. Нехай
х)х(
=
α
,
х2sin)х(
=
β
, де
0х
→
.
2)x/x2(sinlim
0х
=
→
. Отже, нескінченно малі х і sin2x одного по-
рядку.
Визначення 2. Якщо
0/lim
ах
=
→
αβ
, то нескінченно мала β вищо-
го порядку мализни, ніж нескінченно мала α.
Приклад. Нехай
х
=
α
,
n
х=
β
,
1n
>
,
0х
→
. Тоді
0xlimx/xlim
1n
0х
n
0х
==
−
→→
.
Тобто, нескінченно мала α
нижчого по-
рядку мализни, ніж нескінченно мала β.
Визначення 3. Нескінченно мала β k -го
порядку мализни відно-
сно нескінченно малої α, коли β і α
k
- нескінченно малі одного порядку.
Приклад. Нехай
х
=
α
,
3
х=
β
. Коли
0х
→
величина
β
є не-
скінченно мала третього порядку мализни відносно нескінченно малої
α.
Визначення 4. Величини α і β звуть еквівалентними нескінченно
малими і пишуть
β
α
∼
, якщо
1/lim
ах
=
→
αβ
.
Приклад. Показати, що
2
х/)1х( +=
α
і
х/1=
β
еквівалентні
нескінченно малі величини, коли
∞
→
х
.
Розв’язання.
=+=
∞→∞→
)х/1/()х/)1х((lim/lim
2
хх
βα
1)х/11(limх/)1х(lim
хх
=+=+=
∞→∞→
.
Дані величини еквівалентні.
Зауваження 1. Якщо відношення двох нескінченно малих α і β
не має границі і не прямує до нескінченності, то α і β непорівнянні між
собою.
Приклад.
х)х(
=
α
,
)х/1sin(х)х( =
β
при
0х
→
.
Зауваження 2.
Нескінченно великі і нескінченно малі величини
порівнюють між собою однаково.

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
43
ЛЕКЦІЯ № 8
Неперервність функцій. З поняттям границі функції тісно пов'я-
зане інше важливе поняття математичного аналізу - поняття непере-
рвності функції.
Поняття неперервності функції. Розглянемо функцію у = f(х), визна-
чену на деякому проміжку. Нехай x
0
деяка точка цього проміжку, в якій
функція має значення у
0
= f(х
0
).
Якщо x одержить деякий додатний або від'ємний - не має значення - приріст
х
∆
і матиме значення
ххх
0
∆
+=
,
то і функція у одержить деякий приріст
у
∆
. Нове значення функції буде
)xx(fуу
00
∆∆
+=+
(рис. 2.21).
Рис. 2.21
Визначення. Функція у = f(х) неперервна у точці х
0
, якщо вона
визначена у деякому околі точки х
0
(очевидно, і у самій точці х
0
) і як-
що
0уlim
0х
=
→
∆
∆
. Тут
)x(f)xx(fу
00
−+=
∆∆
(2.1)
Умову (2.1) можна записати так:
)x(f)xx(flim
00
0х
=+
→
∆
∆
, тут
0
ххх −=
∆
. (2.2)
Тому
)x(f)x(flim
0
хх
0
=
→
, але
xlimх
0
хх
0
→
=
Рівність (2.2) можна переписати так:
)x(f)xlim(f)x(flim
0
хххх
00
==
→→
. (2.3)
тобто, для того, щоб знайти границю функції коли
0
хх →
, достатньо у
вираз функції підставити замість аргументу х його значення х
0
.
Приклад.
Доведемо, що функція у = sinx неперервна у довільній
у
х
у
0
+∆у
у=f(х)
∆
у
у
0
0
х
0
+∆х
х
0
∆
х
М
М
0
N

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
44
точці х
0
. Справді,
00
xsinу =
,
)xxsin(yу
00
∆∆
+=+
,
)2/xxcos()2/xsin(2xsin)xxsin(y
000
∆∆∆∆
+=−+=
. Раніш було
доведено, що
0)2/xsin(lim
0
х
=
→
∆
∆
. Величина
)2/xxcos(
0
∆
+
обмеже-
на. Отже,
0ylim
0х
=
→
∆
∆
.
Аналогічним чином, розглядаючи кожну основну елементарну
функцію, можемо довести, що вона неперервна у кожній точці свого
визначення.
Спираючись на властивості границі, можна довести такі теоре-
ми.
Якщо функції f
1
(x), f
2
(x) неперервні у точці х
0
, то функції
)x(f)x(f)х(
21
±=
ψ
, або
)x(f)x(f)х(
21
⋅=
ψ
, або
)x(f/)x(f)х(
21
=
ψ
, якщо
0)x(f
2
≠
, також є неперервні у точці х
0
.
Якщо
)x(u
ϕ
=
неперервна у точці х
0
і f(u) неперервна у точці
)x(u
00
ϕ
=
, то й складна функція
))x((f
ϕ
неперервна у точці х
0
.
Таким чином, будь-яка елементарна функція неперервна у кож-
ній точці, у якій вона визначена.
Визначення. Якщо функція у = f(x) неперервна у кожній точці
деякого інтервалу (а, b), де а < b, то кажуть, що функція неперервна на
цьому інтервалі.
Однобічна неперервність. Нехай функція f(x) визначена на проміжку
(а; х
0
]. Кажуть, що функція f(х) неперервна у точці х
0
ліворуч, якщо
)x(f)x(flim
0
0хх
0
=
−→
. (2.4)
Аналогічно, функція f(x), визначена на проміжку [x
0
;b), непере-
рвна в точці x
0
праворуч, якщо
)x(f)x(flim
0
0хх
0
=
+→
. (2.5)
Якщо функція f(x) визначена на інтервалі (а;b) і точка
)b;а(х
0
∈
, то для неперервності функції у точці х
0
необхідно і достат-
ньо, щоб функція f(x) була неперервна ліворуч і праворуч від точки х
0
.
Якщо рівність (2.4) або рівність (2.5) не виконується, то кажуть
що функція f(x) розривна у точці х
0
ліворуч або - праворуч. Точка х =
х
0
, у цьому випадку зветься точкою розриву функції.
Класифікація розривів функції. Розрізняють такі види розривів
функції у точці: розриви першого роду і розриви другого роду. Коли
функція f(х) у точці х
0
не визначена або має стрибок скінченої величи-
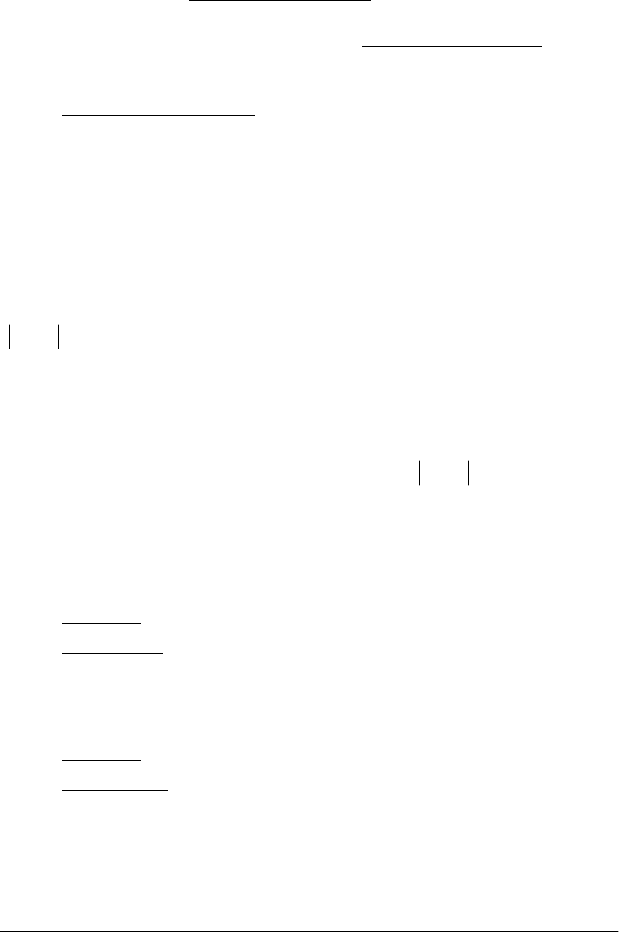
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
45
ни, то кажуть, що це розрив першого роду. Якщо функція у точці х
0
не
має хоча б однієї з односторонніх границь, або вона дорівнює
±∞
, то
кажуть, що функція f(x) має у точці х
0
, розрив другого роду. У обох
випадках точка х
0,
може як належати, так і не належати області визна-
чення функції.
Розриви першого роду.
Границі функції f(x) ліворуч і праворуч від точки
)b;а(х
0
∈
іс-
нують і скінченні.
А)x(flim
0хх
0
=
−→
,
В)x(flim
0хх
0
=
+→
,
А)x(f
0
=
або f(x
0
) = В.
А)x(flim
0хх
0
=
−→
,
В)x(flim
0хх
0
=
+→
,
А)x(f
0
≠
або
В)x(f
0
≠
.
А)x(flim
0хх
0
=
−→
,
А)x(flim
0хх
0
=
+→
,
В)x(f
0
=
.
У цих випадках функція у точці х
0
має стрибок, який дорівнює
В А
−
.
Границі функції f(х) ліворуч і праворуч від точки
)b;а(х
0
∉
:
)b;x()x;a()f(D
00
∪=
існують і скінченні.
А)x(flim
0хх
0
=
−→
,
B)x(flim
0хх
0
=
+→
.
Тут функція має стрибок, який дорівнює
В А
−
.
А)x(flim)x(flim
0хх0хх
00
==
+→−→
.
Тут
0
x
- точка усувного розриву, бо поклавши f(x
0
) = А, діста-
немо неперервну функцію.
Приклад. З'ясувати, який розрив має функція
х/1
2у =
.
Розв’язання. Ця функція не визначена у точці
0
х
= 0.
Розглянемо:
+∞=
+→
х/1
0x
2lim
;
02lim
х/1
0x
=
−→
. Функція у точці
0
х
= 0 має розрив другого роду (рис.2.22).
Приклад. З'ясувати, який розрив має функція
2
х/1
2у
−
=
.
Розв’язання. Функція не визначена у точці
0
х
= 0 (рис.2.23).
Розглянемо:
02lim
2
х/1
0x
=
−
−→
і
02lim
2
х/1
0x
=
−
+→
. Якщо додамо до
функції рівність f(0) = 0, то дістанемо неперервну функцію у точці
0
х
= 0. Отже, маємо усувний розрив першого роду.

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
46
Рис. 2.22 Рис. 2.23
Деякі властивості неперервних функцій.
Теорема 1. Якщо функція у = f(x) неперервна на відрізку [а;b],
то знайдеться хоча б одна точка x = x
1
, де
]b;а[х
1
∈
така, що значення
функції у цій точці буде влаштовувати нерівності:
)x(f)x(f
1
≥
і знайдеться хоча б одна точка x = x
2
,
]b;а[х
2
∈
така, що значення
функції у цій точці буде влаштовувати нерівності:
)x(f)x(f
2
≤
.
Тоді f(x
1
) матиме назву найбільшого, а f(x
2
) - найменшого зна-
чення функції. Нехай f(х
1
) = М, а f(х
2
) = m. Сенс цієї теореми наочно
ілюструється рис.2.24.
Рис. 2.24
Зауваження.
Твердження теореми може бути невірним, якщо
у
х
1
0
у
х
1
0
у
у=f(х)
х
х
2
х
1
b
а
0
М
m

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
47
(
)
х а;b
∈
.
Теорема 2. Нехай функція у = f(х) неперервна на відрізку [а,b] і
на кінцях його має значення різних знаків f(a) < 0; f(b) > 0, тоді між
точками а і b знайдеться хоча б одна точка x = с, така, що f(с) = 0.
Ця теорема має просту геометричну ілюстрацію (рис.2.25).
Рис. 2.25
Теорема 3. Нехай функція у = f(x) визначена і неперервна на ві-
дрізку [а,b]. Якщо на кінцях цього відрізка функція приймає значення
f(а) = А, f(b) = B і А < B, то яке б не було число (А <
µ
< B) знайдеться
така точка х = d, (a < d < b), що f(d) =
µ
.
Сенс цієї теореми чітко ілюструється рис. 2.25.
ЛЕКЦІЯ № 9
Похідна. Нехай у = f(х),
)b,а(х
∈
і
)b,а(х
0
∈
. Візьмемо довіль-
не
)b,а(х
∈
і складемо різницю
0
хх −
. Це приріст незалежної змінної,
який позначають
х
∆
.
Приріст функції f(х) у точці x
0
позначають
у
∆
. Він дорівнює
у)х(f)хх(f
00
∆∆
=−+
.
Оскільки точка х
0
фіксована, то приріст функції
у
∆
є функцією
приросту аргументу
х
∆
.
Складемо відношення
х/ух/))х(f)хх(f(
00
∆∆∆∆
=−+
,
f
(a)=А
у=f(х)
f(b)=В
c
µ
у
х
d
а
0
b

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
48
яке також буде функцією приросту аргументу
х
∆
.
Визначення похідної. Розглянемо границю виразу при
х
∆
, яке
прямує до нуля довільно. Якщо ця границя існує, то кажуть, що функ-
ція f(x) має похідну у точці х
0
, і записують
)х(fх/уlimх/))х(f)хх(f(lim
0
0х
00
0х
′
==−+
→→
∆∆∆∆
∆∆
. (2.6)
Число
)х(f
0
′
є значення похідної функції f(x) у точці х
0
. Похід-
ну функції у = f(x) у точці х
0
, також позначають
0
хх
(x) fу
=
′
=
або
dx/)х(df
0
.
Якщо існує границя (2.6), то також кажуть, що функція f(х) ди-
ференційована у точці х
0
. Коли функція f(х) диференційована у кожній
точці проміжку (а;b), то кажуть, що вона диференційована у проміжку
(а;b). Похідна функції f(х) диференційованої у проміжку (а;b), сама є
функцією х.
Приклад. Дано функцію у = х
2
. Знайти її похідну і обчислити її,
коли х = 3.
Розв'язання. Для будь-якого х маємо у = х
2
. Якщо аргумент до-
рівнює
хх
∆
+
,
маємо
2
)хх(уу
∆∆
+=+
. Звідси
222
)х(хх2х)хх(у
∆∆∆∆
+=−+=
.
Складемо відношення
хх2х/))х(хх2(х/у
2
∆∆∆∆∆∆
+=+=
.
Обчис-
лимо границю:
х2)хх2(lim
0х
=+
→
∆
∆
. Тобто
х2у =
′
;
632у
3х
=⋅=
′
=
,
або
632)3(fу =⋅=
′
=
′
.
Швидкість руху. Нехай матеріальна точка рухається під дією
деяких сил. Візьмемо який-небудь момент часу t і розглянемо промі-
жок часу
t
∆
від моменту t
0
до моменту
ttt
0
∆
+=
. За цей проміжок
часу точка пройде деякий шлях, який позначимо через
)t(S
0
∆
. За ві-
домим з фізики означенням, відношення
)t(S
0
∆
/
t
∆
є середня швид-
кість руху точки за час
t
∆
. Розглядатимемо дедалі менші проміжки
t
∆
, щоб
t
∆
прямувало до нуля. Границя
)t(V)t(St/)t(Slim
000
0t
=
′
=
→
∆∆
∆
є миттєвою швидкістю точки у момент часу t
0
.
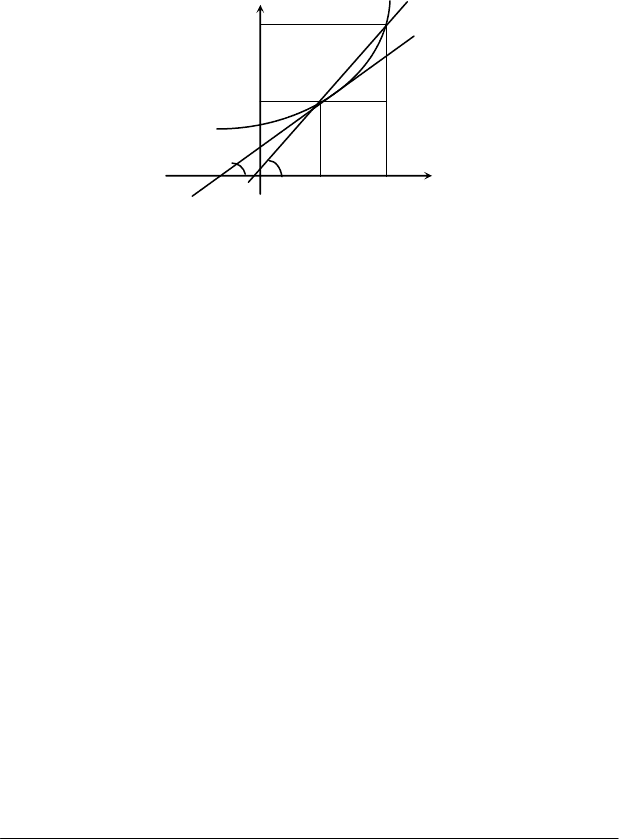
Геометричний сенс похідної. Нехай дано деяку лінію L і на ній
точку М (рис. 2.26). Візьмемо на лінії L деяку точку N, яка не збігаєть-
ся з точкою М. Пряма МN є січною для лінії L. Нехай тепер точка N
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
49
наближається до точки М, залишаючись на лінії L. Тоді кожному по-
ложенню точки N відповідатиме своя січна і усі ці січні проходити-
муть через точку М.
Рис. 2.26
Дотичною до лінії L у точці М звуть граничне положення МK
січної MN, якщо точка N прямує до точки М. Нехай у = f(х) - деяка фу-
нкція, графіком якої є лінія L, диференційована у точці х
0
. У декарто-
вій прямокутній системі координат точка М, яка лежить на графіку
функції у =f(x) і має абсцису х
0
, має координати (x
0
; f(x
0
)). Нехай точка
N належить графіку функції (рис. 2.26) і має координати
)хх(f);хх(
00
∆∆
++
.
Проведемо через точку М пряму, паралельну вісі
Ох, і позначимо точку перетину цієї прямої і прямої
хх
0
∆
+
через Р.
Розглянемо
∆
ΜΝΡ. Відношення його катетів
NP : MP
має вигляд:
α∆∆
tgх/))х(f)хх(f(
00
=−+
. (2.7)
Тобто, це тангенс кута нахилу січної MN до додатного напряму
вісі Ох.
Якщо приріст
0х
→
∆
, то геометрично це означає, що точка
)уу ,хх(N
00
∆∆
++
рухатиметься по лінії L, наближаючись до точки
М, а кут
α
прямуватиме до кута
0
α
- кута нахилу дотичної до додат-
ного напряму вісі Ох.
Оскільки границя рівності (2.7) при
0х
→
∆
з одного боку дорі-
внює
)х(f
0
′
, а з другого боку дорівнює
0
tg
α
, тому
)х(f
0
′
=
0
tg
α
. (2.8)
Використавши формулу (2.8), рівняння дотичної до графіка фу-
нкції у = f(х), яка проходить через точку Μ (х
0
; у
0
), має вигляд:
у
0
х
f(x
0
+∆x)
f(x
0
)
N
L
K
P
M
x
0
+∆x
x
0
α
0
α
