Станішевський С.О. Вища математика. Конспект лекцій. Модуль 1
Подождите немного. Документ загружается.

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
10
Рівняння прямої, яка визначена двома точками.
Нехай маємо дві точки, які не збігаються: А(х
1
, у
1
) і В(х
2
, у
2
).
Треба знайти рівняння прямої у вигляді у = kx + b.
Припустимо, що точка А належить цій прямій, тоді y
1
= kx
1
+ b.
Віднімемо з рівняння (1.2) останнє рівняння. Матимемо:
у – у
1
= k(x – х
1
). Ця пряма проходить крізь точку В(х
2
, у
2
), тобто маємо
тотожність у
2
– у
1
= k(x
2
– х
1
), звідки
k = (у
2
– у
1
)/(x
2
– х
1
).
Таким чином, шукане рівняння має вигляд:
у
– у
1
= (у
2
– у
1
)(x – х
1
)/(x
2
– х
1
), або
(у – у
1
)/(у
2
– у
1
) = (x – х
1
)/(x
2
– х
1
) . (1.4)
Приклад. Знайти рівняння прямої, яка визначена двома точками
А(–1,2) і B(2,5).
Розв'язання. Скористаємося рівнянням (1.4):
3ху1х2у)12/()1х()25/()2у(
+
=
⇒
+
=
−
⇒
+
+
=
−
−
.
З рівняння (1.4) маємо необхідну і достатню умову того, що три
точки А(х
1
, у
1
), В(х
2
, у
2
), С(х
3
, у
3
) належать до однієї прямої:
(x
3
– х
1
)/(x
2
– х
1
) = (у
3
– у
1
)/(у
2
– у
1
).
Рівняння прямої, яка проходить через задану точку А(х
1
, у
1
) у ві-
домому напрямі k.
Рівняння прямої будемо шукати у вигляді (1.2). Невідоме b зна-
ходимо з умови проходження прямої через точку А(х
1
, у
1
):
11
kxуb −=
.
Таким чином, маємо:
11
kxуkxу −+=
або
)xх(kуу
11
−=−
. (1.5)
Тангенс кута між двома прямими. Нехай маємо дві прямі:
11
bxkу +=
і
22
bxkу +=
, які зображено на рис. 1.5. Нехай φ - кут, на
який треба повернути проти стрілки годинника пряму І до прямої II,
щоб вони збіглися. Тоді
12
ααϕ
−=
. Обчислимо tgφ:
)tgtg1/()tgtg()(tgtg
121212
ααααααϕ
+−=−=
, але
11
ktg =
α
, а
22
ktg =
α
. Тобто:
)kk1/()kk(tg
1212
+−=
ϕ
. (1.6)
З останнього виразу випливають дві умови:
умова їх паралельності
12
kk =
;
(1.7)
умова їх перпендикулярності
2 1
k k 1
= −
. (1.8)
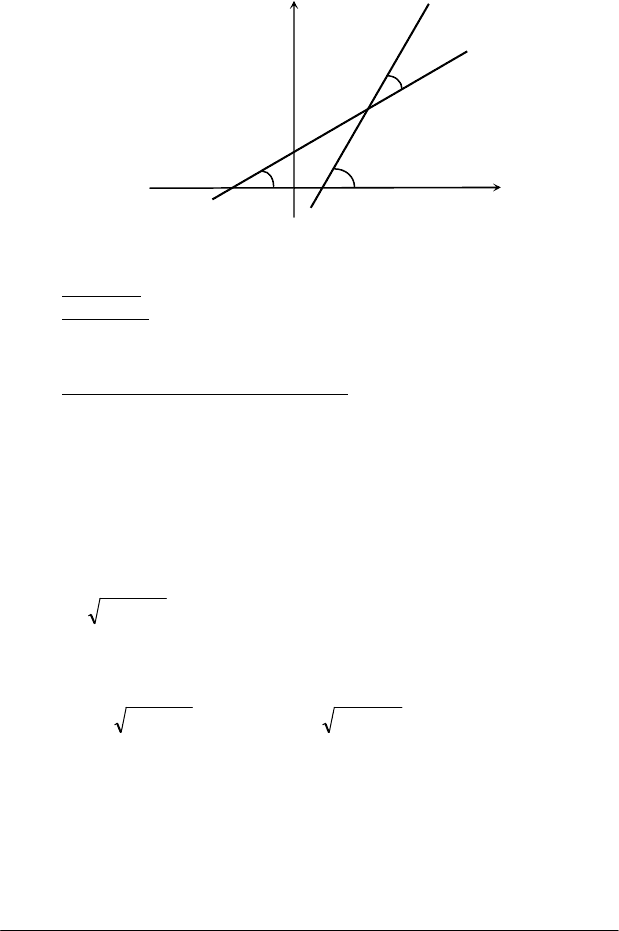
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
11
Рис. 1.5
Приклад. Знайти кут між прямими y = 2x – 3 і у = –3х+2.
Розв’язок. Тут k
1
= 2, a k
2
= –3. Підставимо їх у формулу (1.6):
1)2)3(1/()23(tg
=
−
+
−
−
=
ϕ
. Тобто, tgφ = 1. Відкіля φ = 45
0
.
Нормальне рівняння прямої лінії. Рівняння (1.1) помножимо на
число
ОМ
≠
:
0МСМВуМАх
=
+
+
.
Нехай: МА = cosα, ΜВ = sinα i МС = –р. Тоді:
0рnуsiхcоs
=
−
+
α
α
, (1.9)
це нормальне рівняння прямої. Знайдемо М:
α
22
cоs)МА( =
,
α
22
sin)МВ( =
. Додамо ці вирази:
1sincоs)МВ()МА(
2222
=+=+
αα
. Звідки M
2
(A
2
+ B
2
) = 1, або
)ВА/(1М
22
+±= .
Число Μ звуть нормуючим множником, його знак беруть проти-
лежним знаку вільного члена С.
З'ясуємо, що це за кут α? Тут МА = cosα, a МB =sinα, або
)ВА/(Аcos
22
+±=
α
, )ВА/(Вsin
22
+±=
α
.
Поділимо ці вирази:
А/Вcos/sin
=
α
α
;
1
kА/Вtg ==
α
.
У рівнянні (1.2) мали k = –A/В. Якщо перемножити
k
і
1
k
, ма-
тимемо (1.8). Тобто кут α має пряма y = k
1
x, яка перпендикулярна до
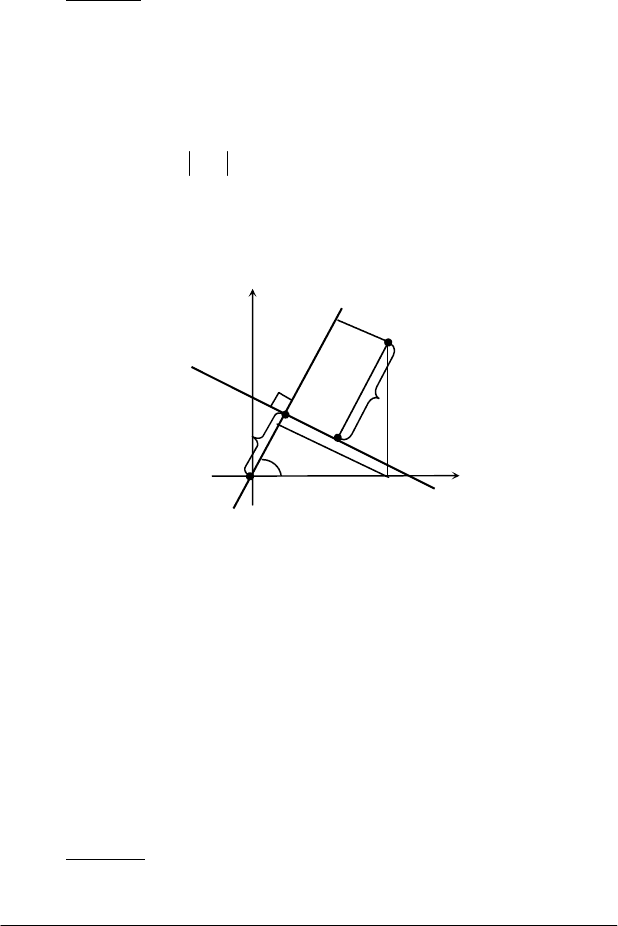
прямої (1.2). Довжина відрізка від початку координат до точки перети-
ну цих прямих дорівнює –р (рис. 1.6).
y
α
1
x
0
φ
α
2
II
I
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
12
Відстань від довільної точки М(x
1
, y
1
) до прямої (1.1).
Позначимо шукану величину через d. Тоді, якщо
0СВуАхМ
=
+
+
∈
, матимемо d = 0.
Нехай точка і пряма розташовані так, як зображено на рис. 1.6.
Позначимо дану пряму – II. Пряму, яка їй перпендикулярна - І.
Розглянемо ламану замкнену лінію OPKMRO. На прямій ОР ви-
беремо додатній напрям від точки О до Ρ і позначимо цю вісь буквою
ℓ. Довжина відрізка
КМ
= d. Спроектуємо замкнену ламану лінію на
вісь ℓ. Відомо, що сума проекцій (позначимо її
Пр
l
)замкненої ламаної
дорівнює нулю. Запишемо це:
Пр ОР Пр РК Пр КМ Пр
MR
Пр
R
О
0
+ + + + =
l l l l l
.
Рис. 1.6
Розглянемо кожну проекцію:
Пр ОР р
=
l
;
Пр КМ
d
=
l
;
Пр РК
0
=
l
;
1
Пр
MR NQ y sin
α
= − = −
l
;
1
Пр
R
О
NO
х
cos
α
= − = −
l
.
Додамо знайдені величини:
0cosxsin
у
dp
11
=−−+
αα
З останнього виразу маємо;
|
р
cosxsin
у
| d
11
−+=
αα
. (1.10)
Таким чином, щоб знайти d, треба рівняння (1.1) привести до
вигляду (1.10) і замість координат х і у підставити координати х
1
і у
1
точки М. Число d матиме знак "+", якщо М(x
1
,y
1
) і О(0,0) розташовані
по різні сторони від прямої II, і знак "–" у протилежному випадку.
Оскільки d - відстань, то праворуч у (1.10) взято абсолютну величину.
Приклад.
Знайти відстань від точки А(1,2) до прямої
3х – 4у + 10 = 0.
y
x
0
α
II
I
Q
P
K
R
N
M(x
1
,y
1
)
d
ℓ
–р

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
13
Розв'язок:
5/125/1))4(3/(1
М
2/122
−=−=−+−= ;
1|1||10)/583(||1/5)(101/5)(421/5)(31|d
=
−
=
−
+
−
=
−
⋅
+
−
⋅
⋅
−
−
⋅
⋅
=
.
Взаємне розміщення двох прямих на площині.
Нехай маємо дві прямі:
А
1
х + В
1
у + С
1
= 0, А
2
х + В
2
у + С
2
= 0.
Розглянемо систему двох лінійних рівнянь:
1 1 1
2 2 2
А х В у С
0,
А х В у С
0.
+ + =
+ + =
Можливі такі випадки:
прямі перетинаються, якщо
1 2 1 2
А
/
А В
/
В
≠ ;
прямі паралельні, якщо
1 2 1 2 1 2
А
/
А В
/
В С
/
С
= ≠ ;
прямі збігаються, якщо
1 2 1 2 1 2
А
/
А В
/
В С
/
С
= = .
Приклад. З'ясувати, як розташовані прямі:
5x3y
−
=
,
4y2x
=
+
.
Розв'язок. Складемо систему
3x y 5,
x 2y 4
− =
+ =
. Тут
3 1
1 2
≠ −
.
Отже, маємо перший випадок. Систему розв’язуємо шляхом ви-
ключення невідомих. Маємо:
27/14x
=
=
;
17/7y
=
=
.
Висновок. Прямі перетинаються. Точка перетину М (2;1).
ЛЕКЦІЯ № 3
Лінії другого порядку на площині. Розглянемо рівняння
0L
Ку
Dx
СуВхуАх
22
=+++++
, де
0
СВА
222
≠++
, це многочлен
другого степеня. Як було сказано вище, він визначатиме (в залежності
від коефіцієнтів) відомі криві другого порядку: коло, еліпс, гіперболу
або параболу. Розглянемо їх.
Коло - це множина всіх точок площини, які лежать на даній до-
датній відстані (радіус) від даної точки площини.
Виведемо рівняння кола. Нехай: М(х, у) довільна точка кола;

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
14
О(а, b) – центр і R - радіус. Із визначення кола запишемо співвідно-
шення:
ОМ
R
=
;
( ) ( )
2 2
х а у b R
− + − =
. Звідки
222
)bу()ах(R −+−=
, (1.11)
яке і є канонічним рівнянням кола.
Приклад. Записати канонічне рівняння кола, якщо його радіус
R=3 і центр знаходиться у точці О(1,-2).
Розв’язання. Підставимо дані величини у (1.11). Маємо каноніч-
не рівняння кола:
9)2у()1х(
22
=++−
.
Еліпс – це множина точок площини, для яких сума відстаней від
двох даних точок площини (фокусів) дорівнює 2а.
2
а 0
>
і більша за
відстань між фокусами.
Канонічне рівняння еліпса. Нехай на площині взято прямокутну
систему координат Оху, а точки F
1
(-с;О) і F
2
(с;О) - фокуси еліп-
са(рис.1.7). Якщо М(x,y) - довільна точка еліпса, то, згідно з означен-
ням еліпса, виконується рівність
.а2МFМF
21
=+
(1.12)
Рис. 1.7
Відрізки [F
1
M] і [F
2
M] є фокальні радіуси еліпса, довжини
яких обчислюємо за формулами:
( )
2
2
1
усхМF ++=
,
( )
2
2
2
усхМF +−=
.
Підставимо ці вирази у рівність (1.12) і виконаємо відповідні
перетворення:
( ) ( )
2
2
2
2
усха2усх +−−=++
;
( )
2222
2
2222
уссх2хусха4а4усхс2х ++−++−−=+++
;
y
x
B
b
M(x,y)
A
a
c
-c
F
1
F
2
-b
-a
a
e
a
e

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
15
( )
сх4а4усха4
22
2
−=+−
;
(
)
(
)
.саауахса
22222222
−=+−
.
Розділимо обидві частини останньої рівності на величину
(
)
222
аса −
і позначимо
222
саb −=
(тут а > с), матимемо канонічне
рівняння еліпса:
1b/уа/х
2222
=+
. (1.13)
Точки перетину еліпса з його вісями симетрії (рис.1.17), які
співпадають з вісями координат Ох і Оу, є вершинами еліпса. Вони
мають координати: (а;О), (-а;О), (О;b), (O;-b). Відрізок |ОА|=а звуть
великою піввіссю еліпса, а відрізок |ОВ|=b - малою піввіссю еліпса.
Точка О є центр еліпса. Еліпс є центрально-симетричною фігурою від-
носно центру.
Ексцентриситет еліпса це відношення відстані між фокусами
еліпса до довжини його великої осі:
1)а2/()с2(е <=
, або
2
)a/b(1е −=
. (1.14)
Ексцентриситет характеризує форму еліпса: чим ближчий екс-
центриситет до одиниці, тим менше відношення b/а і тим більше еліпс
витягнутий; чим менший ексцентриситет, тим ближче відношення b/а
до одиниці і тим ближче еліпс за формою наближається до кола.
Директриси еліпса. Припустимо, що еліпс, заданий канонічним
рівнянням (1.13), має а >b. Тобто, він має таку форму, як на рис.1.7.
Дві прямі, перпендикулярні до великої вісі еліпса (у цьому випадку
вісі Ох) і розміщені на відстані а/e від центра еліпса, звуть директри-
сами еліпса. Рівняння директрис еліпса мають вигляд:
е/ах
±
=
. (1.15)
Оскільки для еліпса е<1, то директриси розміщені зовні від еліпса.
Властивість директрис еліпса. Якщо r - відстань від довільної
точки еліпса до якого-небудь фокуса, d - відстань від тієї самої точки
до директриси, яка відповідає цьому фокусу, то відношення r/d є стала
величина, яка дорівнює ексцентриситету еліпса: r/d = е.
Приклад. Скласти канонічне рівняння еліпса, велика піввісь
якого дорівнює 3, а фокус знаходиться у точці
)0 ,5(F
.
Розв'язок. Канонічне рівняння еліпса має вигляд (1.13). За умо-
вою задачі велика піввісь а = 3, а половина фокусної відстані
5с =
.
Ці величини зв'язані співвідношенням
222
bас −=
. Підставивши дані
величини, маємо
(
)
453b
2
22
=−=
. Шукане рівняння еліпса:

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
16
14/у9/х
22
=+
.
Гіпербола – це множина точок, для яких абсолютна величина рі-
зниці відстаней від двох даних точок площини (фокусів) дорівнює 2а.
2
а 0
>
і менша за відстань між фокусами.
Канонічне рівняння гіперболи. Нехай на площині узято прямо-
кутну декартову систему координат Оху (рис. 1.18), а точки F
1
(–c;O) і
F
2
(c;O) - фокуси гіперболи. Множина точок М(х,у), які згідно з озна-
ченням утворює гіперболу, задовольняє рівняння
.а2МFМF
21
=−
(1.16)
Відрізки F
1
М і F
2
М є фокальні радіуси гіперболи. Обчисливши
їх довжину, маємо рівняння
( ) ( )
а2усхусх
2
2
2
2
=+−−++
.
Перетворення цього рівняння аналогічні тим, що робилися з рі-
внянням (1.12) еліпса. Звільнившись від ірраціональностей, рівняння
зводимо до вигляду
(
)
(
)
22222222
асауахас −⋅=−⋅−
. Позначивши
)aс(bас
222
>=−
, і поділивши останнє рівняння на
(
)
2 2 2
а c a
⋅ −
, зво-
димо його до канонічного рівняння гіперболи:
1b/уа/х
2222
=−
. (1.17)
Точки перетину гіперболи з віссю Ох є вершини гіперболи (на
рис. 1.8 це точки А
1
(-а;О) і А
2
(а;О) відповідно). Точка О є центр гіпер-
боли. Відрізок |A
1
A
2
| є дійсною віссю гіперболи, а відрізок |В
1
В
2
| є
уявною віссю гіперболи. Прямокутник зі сторонами 2a і 2b, розміще-
ний симетрично відносно осей гіперболи, звуть основним прямокутни-
ком гіперболи.
Рис. 1.8
В
1
-b
А
1
0
b
у
х
В
2
а
с
-а
-
с
F
2
F
1
А
2
М(х,у)

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
17
Асимптоти гіперболи. Гіпербола є центрально-симетричною фі-
гурою і має дві вітки. Вітки гіперболи, що лежать у першій і третій
координатних чвертях, при нескінченному зростанні х наближаються
до прямої у=(b/a)x. Вітки гіперболи, що лежать у другій та четвертій
координатних чвертях, при нескінченному зростанні x наближаються
до прямої у=(-b/a)x. Ці прямі звуть асимптотами гіперболи. Подамо
загальне визначення асимптоти.
Асимптота графіка функції у = f(х) є пряма, яка має таку власти-
вість, що відстань від точки на графіку (х, f(х)) до цієї прямої наближа-
ється до нуля, якщо ця точка рухається вздовж вітки графіка до не-
скінченності.
Тобто, рівняння асимптот гіперболи знаходимо з рівняння
(1.17), розв'язавши його відносно у:
( ) ( )
2
х/а1хa/bу −⋅±=
.
Зробивши граничний перехід, коли х прямує до нескінченності, маємо
рівняння асимптот гіперболи:
(
)
хa/bу ±=
. (1.18)
Ексцентриситет гіперболи є відношення відстані між її фокуса-
ми до відстані між вершинами цієї гіперболи:
1)а2/()с2(е >=
, або
( )
2
a/b1е +=
. (1.19)
Ексцентриситет гіперболи характеризує форму її основного
прямокутника, а отже , і форму самої гіперболи: чим менший ексцент-
риситет гіперболи, тим більше витягнутий її основний прямокутник у
напрямі осі, яка з'єднує вершини.
Якщо b = a, то гіперболу звуть рівносторонньою.
Директриси гіперболи. Дві прямі, перпендикулярні до дійсної
осі гіперболи і розміщені на відстані а/е від центра гіперболи, звуть
директрисами гіперболи.
Рівняння директрис у прямокутній системі координат, відносно
якої гіпербола задається канонічним рівнянням (1.17), мають вигляд:
е/ах
±
=
. (1.20)
Оскільки для гіперболи е > 1, то директриси розміщені між вершинами
гіперболи (рис. 1.8). Директриса гіперболи має таку властивість: якщо
r - відстань від довільної точки гіперболи до якого-небудь фокуса, d -
відстань від тієї самої точки до директриси, яка відповідає цьому фо-
кусу, то відношення r/d - стала величина, яка дорівнює ексцентрисите-
ту гіперболи. Тобто, r/d=e.
Приклад.
Точки

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
18
М(5,8/3) і N(–4,(2
7
/3)) належать гіперболі. Знайти її канонічне рів-
няння, ексцентриситет, рівняння асимптот і директрис, якщо вісі коор-
динат є вісями симетрії гіперболи.
Розв'язок. Канонічне рівняння гіперболи будемо шукати у ви-
гляді (1.17). Оскільки точки Μ і N належать до гіперболи, то маємо
тотожності:
(
)
1b/3/8а/5
2
2
22
=−
і
( )
(
)
1b/3/72а/4
2
2
2
2
=−−
.
Це система двох рівнянь з двома невідомими
2
а
і
2
b
. Нехай
uа/1
2
=
і
vb/1
2
=
, тоді:
(
)
( )
25u 64 / 9 v 1,
16u 28 / 9 v 1.
− =
− =
Розв'язок цієї системи дає:
9/1u
=
,
4/1v
=
. Тобто, а
2
= 9 і b
2
= 4 і канонічне рівняння гіперболи матиме вигляд
.14/у9/х
22
=−
Обчислимо ексцентриситет за формулою (1.19):
е 13 / 3.
=
Рівняння асимптот:
(
)
х3/2у ±=
.
Рівняння директрис:
(
)
х 9 13 / 13
= ±
.
Парабола – це множина точок площини, для яких відстань до
заданої точки F (фокуса), дорівнює відстані до певної заданої прямої
(директриси).
Відстань
p
(
0р
≠
) від фокуса F до директриси параболи є па-
раметр параболи. Таким чином, множина точок М, які утворюють па-
раболу, відповідно до означення параболи, задовольняє рівняння:
/FM/ = /MN/ . (1.21)
Канонічне рівняння параболи. Нехай на площині узято прямо-
кутну декартову систему координат Оху, а точка F (p/2; 0) - фокус па-
раболи; пряма х = –р/2, є директриса параболи (рис.1.9). Координати
будь-якої точки М(x, y), яка належить параболі, задовольняють рівнян-
ня (1.21). Отже, маємо:
( )
2/рху2/рх
2
2
+=+−
.
Звільнившись від ірраціональності, останнє рівняння зводимо до вигляду
рх2у
2
=
, (1.22)
яке є канонічним рівнянням параболи. Вісь симетрії параболи (у дано-
му випадку це вісь Ох) є вісь параболи. Точка перетину параболи з
віссю симетрії є вершина параболи.

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
19
Зазначимо (згідно з означенням параболи і властивостями дире-
ктрис еліпса і гіперболи), що парабола має ексцентриситет, який дорі-
внює одиниці.
Рис. 1.9
Приклад. Скласти канонічне рівняння параболи, у якої рівняння
директриси х = –4.
Розв'язок. Оскільки рівняння директриси х = –р/2, то –р/2 = –4.
Звідси р = 8. Вісь симетрії параболи співпадає з віссю Ох. Таким чи-
ном,
рх2у
2
=
або
х16у
2
=
є шукане рівняння.
ЛЕКЦІЯ № 4
Полярна система координат. Щоб визначити положення точ-
ки на площині, крім розглянутої вище прямокутної системи координат,
ще є полярна система координат. Визначимо її. Для цього візьмемо на
площині довільну точку О, яку звуть полюсом, і направлений промінь
ОР, який звуть полярною віссю. На ній відкладемо відрізок ОЕ який
звуть одиничним або масштабним відрізком (рис.1.10).
Рис. 1.10
у
х
М(х,у)
0
F(р/2,0)
N(
-р/2,у)
-р/2
0
E
P
M (r,φ)
φ
M
0
(3,π/6)
3
r
