Skiadas C.H., Skiadas C. Chaotic Modelling and Simulation. Analysis of Chaotic Models, Attractors and Forms

Подождите немного. Документ загружается.

174 Chaotic Modelling and Simulation

(a) a = 1, t = 10 (b) a = 0.25, t = 100

FIGURE 8.13: Rotations

and the resulting diﬀerential equation for x, y:

x∆θ

a − y∆θ

This equation leads to the following form

ady = (∆θ)rdr

The solution of this diﬀerential equation depends on the form of the function ∆θ. In

this section, we use a function known from mechanics, that deals with the rotation

angle. This function arises from the law related to the transverse component of the

acceleration in a circular movement. The function is expressed by the formula

θ =

where c

is a constant. Provided that ∆t = 1, the following approximation for ∆θ is

obtained

∆θ ≈

Finally, we proceed to the solution of the equation:

ady =

The solution is

ln(r) = ay + h (8.20)

where h is an integration constant.

This last equation can be transformed in the following form:

ln(x

+ y

) = ay + h (8.21)

Rotations 175

Exploring the properties of this last equation, we set x = 0 when y = r. In this

case the maximum or minimum values of y are obtained. The resulting equation for

y is

ln(y) = ay + h

The maximum value for y is achieved when y =

. Then, the value of the para-

meter h at this limit is

crit

= c



− 1



This value of h

crit

, applied to equation (8.21), gives an equation for the path of a

trajectory in the (x, y) plane, which divides the plane in two segments. This trajectory

is the outer limit of the vortex region of the rotation. When h > h

crit

, the trajectories

diverge and the rotating object heads oﬀ to inﬁnity. When h < h

crit

, the object rotates

inside the limits set by the above trajectory.

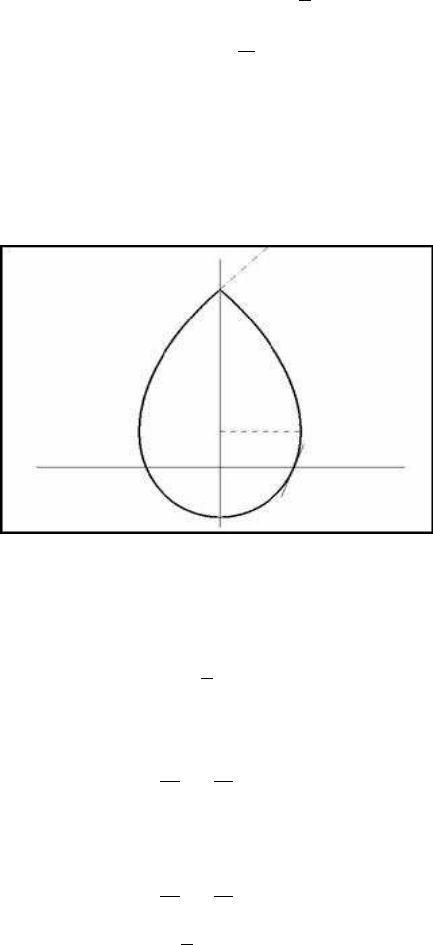
FIGURE 8.14: The characteristic trajectory

Some very interesting properties of the two-dimensional function are illustrated in

Figure 8.14. The trajectory in the limit of escape is shaped as an egg. The sharper

corner is at the maximum value of y =

where x = 0. These values of x, y set the

derivatives ˙x , ˙y equal to zero. However, this point is not stable. This maximum value

is obtained by solving the following equation for y:

−

+ 1 = 0

The minimum value of y is obtained when the rotation speed is maximum. The

resulting equation for y is:

+ 1 = 0

A numerical solution gives y = 0.278

176 Chaotic Modelling and Simulation

The maximum x

max

is estimated by equating to zero the ﬁrst derivative of the

following equation for x, y:

ln(x

+ y

) = ay + c





− c

After appropriate diﬀerentiation, a numerical solution of the resulting equation gives

max

= 0.402

. This is achieved at y = 0.203

When y = 0, then x =

. The tangent at this point is

= e. This tangent appears

in Figure 8.14.

The tangent at the top sharp corner of the egg-shaped form can be computed as

before, using Taylor approximation of the curves in a neighbourhood of the point





. Setting z = y −

, equation (8.21) becomes:







+ z

+ 2

z +







= az + c

+ h (8.22)

Using the expansion

(

a + x

)

= ln(a) +

−

+ ···

where a =

and x = x

+ z

+ 2

z, we see that equation (8.22) becomes:

az + c

+ h =















+ z

+ 2



−



+ z

+ 2



+ ···

Finally, after simpliﬁcation, this becomes:

0 =



− 2z

+ ···



In other words, the two tangent lines at the point (x, z) = (0, 0) are given by the

equation:

= 2z

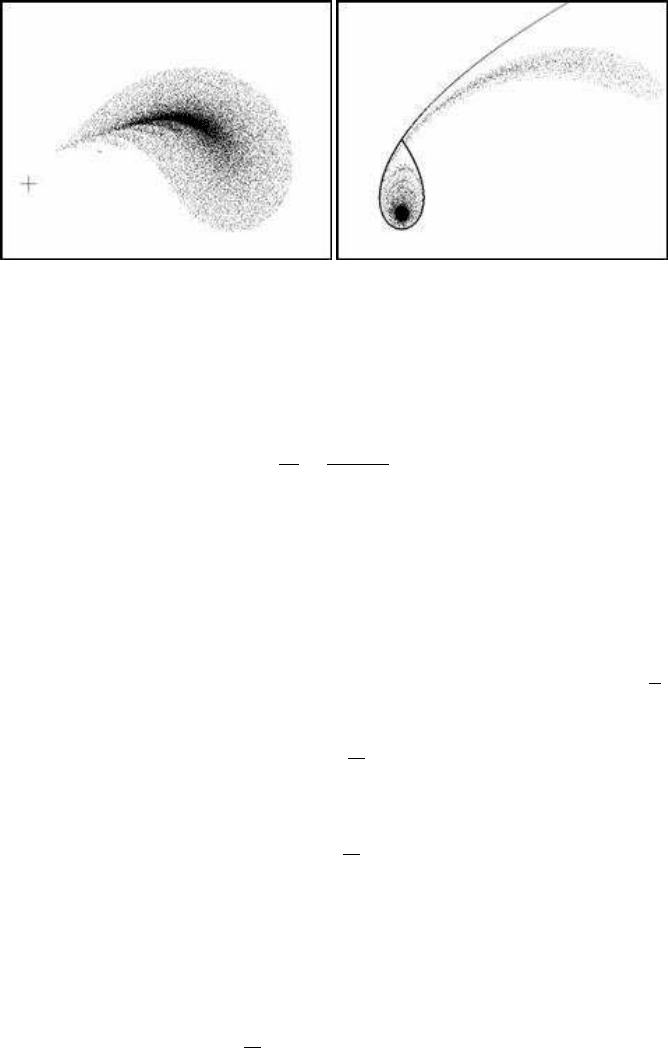
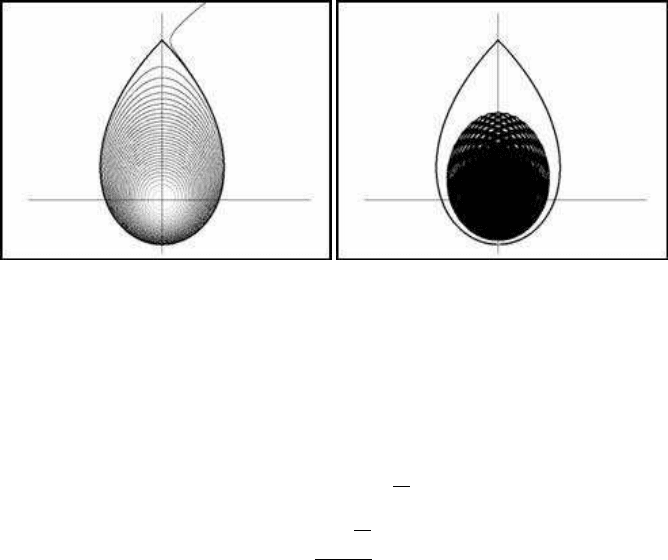
In Figures 8.15(a) and 8.15(b), important properties of the model are presented.

In Figure 8.15(a), the continuous model presented above is simulated. On the other

hand, in Figure 8.15(b), the discrete analogue of the model appears. Figure 8.15(b)

illustrates the central bulge in the case of a = 2.7 and c

= 100. The value of

the translation parameter is quite high. This causes the appearance of an enormous

chaotic attractor in the middle of the egg-shaped area. As in the case discussed

previously, strong bifurcation is present.

As is illustrated in Figure 8.15(a), the particle follows an anti-clockwise direction.

It starts from a point near zero, and it rotates away from the centre until the highest

Rotations 177

(a) The continuous case (b) The central chaotic bulge

FIGURE 8.15: Comparison of the continuous and the discrete models

permitted place. Then, it escapes to inﬁnity following the tangent on the top of the

egg-shaped path. The iterative formula for the above simulations is the following:

n+1

= x



a − y



n+1

= y

+ x

+ y

(8.23)

The parameters in both ﬁgures are a = 2.7, c

= 100 and d = 0.0001.

178 Chaotic Modelling and Simulation

Questions and Exercises

1. Show that the maximum speed in the rotating mass of system (8.7) is obtained

exactly when

y = −

, x = 0

2. Show that for h >

the orbits of system (8.7) go to inﬁnity.

3. Consider the system (8.14), expressed via the simpler form (8.15). Show, by

considering the resulting system for z

−a

ab/(1−b)

, that if f

is within the circle

centred at (a, 0) and with radius

1−b

, then f

n+1

is also within that circle. What

happens with point outside this circle?

4. Derive equation (8.17) for the ﬁxed points of the system (8.14).

5. Show that if z is a complex number, its reﬂection along the line x =

will be

a − ¯z.

6. Construct the level curves in the x, y plane of equation (8.9) for h = 0, and

varying values of a. What is the form of the curves when a = 0?

7. Use the equations (8.7) where

∆θ =

to determine the rotation speed in the x and y directions for the level curves

examined in the previous question.

8. Construct the levels curves in the x, y plane of equation (8.9) when h =

2MG

for various values of a.

9. Draw the level curves (x, y) of equation (8.18) for various values of β, and

especially for β = 1.

10. Following the methodology of section 8.6, draw escape paths of particles

through an egg-shaped form.

11. Construct a rotating model providing an egg-shaped form, and draw a chaotic

bulge and escape paths for both small and large values of the parameter a.

12. Explain why the continuous case of Figure 8.15(a) does not show any chaotic

behaviour.

13. Draw trajectories for the discrete case of Figure 8.15(a).

Chapter 9

Shape and Form

9.1 Introduction

About 2300 years ago, Euclid of Alexandria wrote his famous book on geometry

called The Elements. This book, and its famous ﬁve postulates, became the basis of

what is now known as Euclidean geometry. The usual notion of distance in space,

essential when we design geometric forms in two or three dimensions, carries his

name (the “Euclidean metric”).

The development of science throughout the centuries brought new theories and

improvements in all scientiﬁc ﬁelds. Nevertheless, the Euclidean metric remains

unchanged, and still plays an essential part in a bevy of topics. The theory of the

simulation of chaotic shapes included in this book is based on an analytic approach

that for the most part uses the fundamental notions of traditional Euclidean geom-

etry. The essential components of this theory, namely the notions of translation,

rotation and reﬂection, are deﬁned and explored in this chapter, along with applica-

tions related to the development of chaotic forms and shapes.

As one can readily verify, a large number of chaotic objects that appear in the

literature may be classiﬁed as geometric objects produced by following simple geo-

metric rules. Even non-chaotic objects are similarly simulated by following the same

geometric rules.

Translation, rotation and reﬂection are not only tools essential in forming geomet-

ric objects, but can also be used as a basis of understanding how a process, chaotic

or not, can generate shapes and forms. The linear movements of physical objects

are easily modelled geometrically by using translation. Rotation and translation are

present in stellar systems, galaxies, tornados and vortex movements. Reﬂection is

generally associated with light refraction, galactic object formation, as well as vor-

tex formation.

This chapter includes a brief introduction to the elementary rules of analytical ge-

ometry that are used throughout this book, along with several applications on the

shape and form of chaotic and non-chaotic objects. This theoretical treatment is

combined with applications to special relativity and Penrose’s tiling theory, via sim-

ulations based on relatively simple aﬃne transformations. Interested readers may

ﬁnd related topics in books on hyperbolic geometry.

179

180 Chaotic Modelling and Simulation

9.1.1 Symmetry and plane isometries

Any subset of the plane is called a ﬁgure. It can be easily observed that some

ﬁgures are more interesting than others. Figures with a high degree of symmetry

are most interesting, not only because of interesting forms arising in simulations, but

also because they often occur in nature. Spiral galaxies, snowﬂakes, molecules and

crystals are examples of objects with symmetric cross sections.

By symmetry for a ﬁgure A, we mean simply a transformation that preserves the

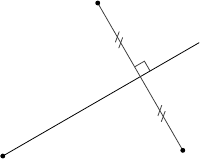
ﬁgure. The simplest kind of symmetry in a plane ﬁgure is that of symmetry with

respect to a line. Two points X and X

′

are symmetrical with respect to a line l, if the

line l bisects and is perpendicular to the segment XX

′

. We will also say that X

′

is the

reﬂection of X along ℓ (Figure 9.1).

ℓ

′

FIGURE 9.1: Symmetry/reﬂection along a line

An isometry is a transformation which preserves distances; i.e. it is a transforma-

tion

T : R

→ R

with the property that the distance from T (A) to T (B) is the same as the distance

from A to B. A standard theorem in Euclidean geometry is that

every planar isometry is completely determined by its eﬀect on three

non-collinear points.

The proof is fairly straightforward and instructive: Since distances are preserved,

the circle centred at A and with a given radius is mapped to the circle centred at

T A, and with the same radius. If we consider the three circles through D, and with

centres A, B, C respectively, and look at their images, then T D must be the point of

intersection of these three circles (Figure 9.2).

Isometries respect the two fundamental aspects of geometry: the incidence aspect

based on the notion of collinearity, and the metric aspect based on the notion of

distance. The fact that isometries respect collinearity is left as an exercise.

There are four basic kinds of planar isometries:

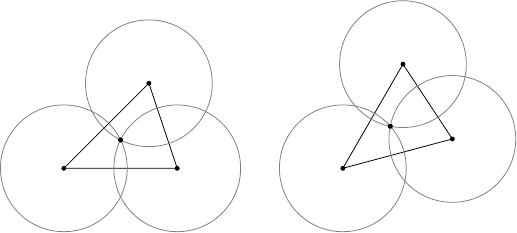
Shape and Form 181

A T A

T B

T D

FIGURE 9.2: Planar isometries are determined by their eﬀect on three points

Translations These are fully described by a single vector

v. Such a transformation

is given simply by:

w =

w +

Rotations These correspond to a rotation with a given angle and around a speciﬁc

point. Assuming the rotation is around the origin, the transformation is given

simply by the matrix:

rot θ =

cos θ − sin θ

sin θ cos θ

in other words:

w = rot(θ)

x cos θ − y sin θ

x sin θ + y cos θ

Reﬂections A reﬂection across a line ℓ passing through the origin and forming angle

θ with the x axis is given by the matrix

ref θ =

cos 2θ sin 2θ

sin 2θ −cos 2θ

and therefore it has the form:

w = ref(θ )

x cos 2θ + y sin 2θ

x sin 2θ − y cos 2θ

Glide Reﬂections A glide reﬂection is a translation followed by a rotation along

a line parallel to the translation direction. The translation and rotation can

be performed in either order. An example of a glide reﬂection is given in

ﬁgures 9.3(a) and 9.3(b). You can see that a glide reﬂection can be thought of

also as the composition of a rotation followed by a reﬂection (or equivalently,

three reﬂections along lines that do not all have a point in common).

182 Chaotic Modelling and Simulation

ℓ

T O

T A

T B

(a) Glide reﬂection as a rotation, fol-

lowed by a reﬂection

ℓ

′

T O

T A

T B

(b) Glide reﬂection as a translation, followed

by a reﬂection

FIGURE 9.3: Glide reﬂection seen in two diﬀerent ways

The matrices rot θ, ref θ have a series of useful properties, which we summarise

here:

rotθrotφ = rot(θ + φ) (9.1)

rot(0) = I (9.2)

refθrefφ = rot(2(θ − φ)) (9.3)

refθrotφ = ref(θ − φ/2) (9.4)

rotφrefθ = ref(θ + φ/2) (9.5)

refθrefφrefy = ref(θ − φ + y) (9.6)

We leave the veriﬁcation of these identities to the reader.

It is worth pointing out that the composition of two reﬂections with the same centre

is a rotation with angle twice the angle between the two reﬂection lines:

ref θ ref φ =

cos 2(θ − φ) −sin 2(θ − φ)

sin 2(θ − φ) cos 2(θ − φ)

= rot 2(θ − φ)

For a geometric proof of this fact, consider the eﬀect of the combined transformation

on the points O, A, B in Figure 9.4(a). The ﬁrst reﬂection, along the line ℓ

, takes the

points O, A, B to the points O, A, B

′

and the second, along the line ℓ

, takes those

Here, as well as in the rest, we will identify a point P(x, y) with the vector

w starting at the origin

and ending at (x, y).

Since a reﬂection ﬁxes all points on the reﬂection line.

Shape and Form 183

points to the points O, A

′

, B

′

. The same eﬀect would be obtained by the aforemen-

tioned rotation.

At this point, you might be wondering, what happens when we take the composi-

tion of two reﬂections along parallel lines. The result is a translation with a vector

twice the distance between the two lines (Figure 9.4(b)).

ℓ

′

(a) The composition of two re-

ﬂections along intersecting lines

is a rotation around the intersec-

tion

ℓ

′′

= A

′

′′

= C

′

(b) The composition of two reﬂections

along parallel lines is a translation

FIGURE 9.4: The composition of two reﬂections

A very striking result is that these four types, along with the identity, are all the

plane isometries, namely:

1. Every plane isometry is a composition of reﬂections.

2. Every composition of reﬂections in the plane can be performed

with at most three reﬂections.

The relation between isometry groups and symmetries is given by the following

theorem, already known to Leonardo da Vinci:

All ﬁnite isometry groups can occur as symmetry groups of ﬁgures, and

cannot contain translations or glide reﬂections.

We ﬁnish this section with a brief discussion of the points and shapes left invariant

by the various isometries. A shape/set S is said to be left invariant by a transforma-

tion T , if the sets T (S ) and S coincide (i.e. if the transformation preserves S as a

whole, though it might move the points of S around). We omit the identity, which

leaves everything ﬁxed.

Points Translations and glide reﬂections have no ﬁxed points. A rotation ﬁxes its

centre, while a reﬂection ﬁxes every point on the line of reﬂection.