Skiadas C.H., Skiadas C. Chaotic Modelling and Simulation. Analysis of Chaotic Models, Attractors and Forms

Подождите немного. Документ загружается.

204 Chaotic Modelling and Simulation

and

n+1

= b −

respectively. Try several values for the parameter a, and explore if there is a

relation between a and b related to the chaotic behaviour of the system.

Chapter 10

Chaotic Advection

10.1 The Sink Problem

Questions related to chaotic advection go back to the nineteenth century and the

development of hydrodynamics, especially the introduction of the Navier-Stokes

equations (Claude Navier, 1821 and George Stokes, 1845). The vortex ﬂow case

and the related forms including vortex-lines and ﬁlaments, vortex rings, vortex pairs

and vortex systems can be found in the classical book by Horace Lamb, ﬁrst edited

in 1879 (Lamb, 1879). However, the formulation of a theory that partially explains

the vortex problem and gives results that coincide with the real life situations has

only been achieved in recent years, thanks to progress in computer simulations. The

introduction of terms like chaotic advection and the blinking vortex system appeared

only in last decades, in order to deﬁne and analyse speciﬁc vortex ﬂow cases.

In most cases, the formulation and solution of the problem followed the diﬀer-

ential equations approach, mostly directed towards the solution of a Navier-Stokes

boundary value problem. Few interesting cases are based on diﬀerence equations

analogues. However, the formulation and analysis of vortex ﬂow problems by means

of diﬀerence equations can be very useful for several cases if a systematic study is ap-

plied. In this chapter we follow the diﬀerence equations methodology by introducing

rotation-translation diﬀerence equations and a non-linear rotating angle, along with

a space contraction parameter, in order to study chaotic advection problems. The

interconnections between the diﬀerence and the diﬀerential equations case is also

studied in speciﬁc cases.

10.1.1 Central sink

Consider a circular bath with a sink in the centre at (x, y) = (0, 0). The water inside

the bath is rotating counterclockwise. A coloured ﬂuid is injected in the periphery

of the bath. The question we propose to address is to determine the shape of the

ﬂuid ﬁlaments if the sink is open. Geometrically the problem is that of rotation with

contraction by a parameter b < 1. The rotation-translation model (9.10) is applied,

The ﬁrst three sections of this chapter have previously appeared in Skiadas (2007).

205

206 Chaotic Modelling and Simulation

with the translation parameter a being zero. The equations of ﬂow would then be:

t+1

= b(x

cos φ

− y

sin φ

)

t+1

= b(x

sin φ

+ y

cos φ

)

(10.1)

The contraction in the radial direction (r =

+ y

) is found from system (10.1):

t+1

= b

+ y

= br

(10.2)

The rotation angle is assumed to follow a function of the form

= c +

. (10.3)

The space contraction is given by estimating the Jacobian of the ﬂow J = b

. When

b < 1, a particle is moving from the periphery of the bath to the sink in the centre

of coordinates following spirals, as illustrated in Figure 10.1(a). The parameters are

b = 0.85, c = 0, d = 0.4, and the initial point is (x

, y

) = (1, 0).

When the same case is simulated for particles entering from the periphery of the

rotating system at time t = 0, 1, 2, . . ., Figure 10.1(b) results. The spiral forms start

from the periphery and are directed towards the central sink. It is also interesting

that full concentric circles appear while the spiraling ﬂow continues. These circles

have a smaller diameter, or even disappear completely, when the rotation parameter

d gets smaller. The parameter b also inﬂuences the spiral. Figure 10.1(c) illustrates

an advection case when b = 0.95, c = 0 and d = 0.01.

(a) Spiral particle paths (b) Spiral forms directed

to the sink

ward a central sink

FIGURE 10.1: Spiral forms

Chaotic Advection 207

10.1.2 The contraction process

From the rotation-contraction equations (10.1) and (10.2), it follows that the radial

contraction is:

∆r

= r

t+1

− r

= br

− r

= −(1 −b)r

The diﬀerential equation for the contraction process is found by observing that:

≈

∆r

∆t

t+1

− r

(t + 1) − t

= −(1 −b)r

The resulting diﬀerential equation expressing the radial speed

˙r = −(1 − b)r

is solved to give

r = r

−(1−b)t

where r

is the initial radius.

The movement is then totally determined, as the equation for the rotation angle has

been given earlier. The paths form spirals towards the centre. When the movement

covers a full circle, the new radius will be:

r = r

−(1−b)

2π

10.2 Non-Central Sink

In the following case, a circular bath with a non-central sink is examined. The

sink is located at (x, y) = (a, 0). The equations of ﬂow are:

t+1

= b



− a) cos φ

− y

sin φ



t+1

= b



− a) sin φ

+ y

cos φ



(10.4)

The rotation angle is assumed to follow an equation of the form

= c +

where r

− a)

+ y

. The ﬁxed points for this map are given by the equation

+ y

= b



(x − a)

+ y



or, after transformation:

x +

1 − b

+ y

1 − b

208 Chaotic Modelling and Simulation

This is the equation of a circle with radius R =

1−b

centred at (x, y) =



1−b

, 0



The ﬂow is not symmetric. The coloured ﬂuid starting from the outer periphery of

the bath approaches the sink in few time periods, as illustrated in Figure 10.2(a). The

parameters are a = 0.15, b = 0.85, c = 0 and d = 0.1. To simplify the process, it is

assumed that the coloured ﬂuid is introduced simultaneously in the periphery of the

bath. Then, the circular form of the original coloured line is gradually transformed

into a chaotic attractor located at the sink’s centre (x, y) = (a, 0). The attractor is

quite stable in terms of form and location.

The attractor appears even if the coloured particles are introduced into a small

region of the bath, as presented in Figure 10.2(b). The coloured particles are intro-

duced in a square region (0.1 × 0.1) at the right end of the bath at (x, y) = (1, 0). The

parameters are a = 0.15, b = 0.85, c = 0 and d = 0.8. As the vortex parameter d is

higher than in the previous case, the chaotic attractor appears at the 6th time step of

the process. The attractor is also larger than in the previous case.

(a) (b)

FIGURE 10.2: Chaotic attractors in a non-central sink

10.3 Two Symmetric Sinks

10.3.1 Aref ’s blinking vortex system

Chaotic mixing in open ﬂows is usually modeled by using the blinking vortex-sink

system, invented by Aref (see Aref, 1983, 1984; Aref and Balachandar, 1986). Aref’s

system models the out-ﬂow from a large bath tub with two sinks that are opened in

Chaotic Advection 209

an alternating manner, in order for chaotic mixing to take place in the course of the

process. To model the velocity ﬁeld caused by a sink, we assume the superposition

of the potential ﬂows of a point sink and a point vortex. If z = x + iy is the complex

coordinate in the plane of ﬂow, the complex potential for a sinking vortex point is

w(z) = −(Q + iK) ln

z − z

where z

= (±a, 0), 2πQ is the sink strength and 2πK the vortex strength. The imag-

inary part of w(z) is the stream function:

Ψ = −K ln r − Qφ

The streamlines are logarithmic spirals deﬁned by the function:

φ = −(K/Q) ln r + const

The diﬀerential equations of motion in polar coordinates are

˙r = −

φ =

(10.5)

and their solutions are:

r =

− 2Qt

φ = φ

−

(10.6)

The ﬂow is fully characterised by the adimensional sink strength η and the ratio of

vortex to sink strength ξ, given by:

η =

, ξ =

(10.7)

The parameter T is the ﬂow period, usually set to 1, and a is the distance of each sink

from the centre of coordinates. As indicated in the literature (K

arolyi and T

el, 1997;

arolyi et al., 2002), chaotic ﬂow appears for parameter values η ≥ 0.5 and ξ = 10.

More precisely, when particles are injected into the ﬂow in few time periods, they

are attracted to a speciﬁc region (the attractor) of the ﬂow system. In recent years,

several studies have appeared investigating this phenomenon both theoretically and

experimentally. The theoretical studies also include simulations using large grids

(1000 ×1000), as well as numerical solutions of the general equations of ﬂow. These

studies suggest that the attractors are time periodic according to the time periodicity

of the ﬂow. However, if only one sink is used, a stable attractor could be present,

both theoretically and experimentally, as the simulations presented above show.

We apply Aref’s blinking vortex system ﬁrst of all to a rotating ﬂuid. We select a

counterclockwise rotation. The symmetric sinks are located at (x, y) = (−a, 0) and

210 Chaotic Modelling and Simulation

FIGURE 10.3: The two symmetric sinks model

(x, y) = (a, 0) and the time period is T = 1. According to this system, the ﬂow is

not stationary and there are jumps in the velocity ﬁeld at each half period T/2. In

other words, a particle located at (−a, 0) appears at (a , 0) in the next time period, as

illustrated in Figure 10.3.

We propose to analyse a discrete time system, like Aref’s system, by using the the-

ory of diﬀerence equations and discrete systems. It is more straightforward to con-

sider the geometry of this system. The model we search must be a rotation-translation

one with a contraction parameter b < 1 expressing the gradual shortening of the ra-

dius r that causes the particles to follow logarithmic spiral trajectories around the

sinking vortices. In accordance with the theory just discussed, a rotation-translation

model of this type is expressed by the diﬀerence equation:

t+1

= a + b(z

− z

iφ

(10.8)

Equation (10.8) can be written as

t+1

+ iy

t+1

= a + b



+ a) + iy



(cos φ

+ i sin φ

) (10.9)

The system of iterative diﬀerence relations for x and y is obtained by equating the

real and imaginary parts of (10.9):

t+1

= a + b(x

+ a) cos φ

− by

sin φ

t+1

= b(x

+ a) sin φ

+ by

cos φ

(10.10)

If a particle is located at (x

, y

) = (−a, 0), then after time t = 1 it will be located

at (x

, y

) = (a, 0). We next need to specify the form of the angle φ

. We will use the

form:

= φ

ηξ

= c +

(10.11)

Chaotic Advection 211

where c = φ

= π is chosen to account for the half-cycle rotation, d = ηξ is the

vortex strength, and r = r

is the distance from the vortex (−a, 0), namely:

r =

(x + a)

+ y

For the experiments presented in the literature, η = 0.5, ξ = 10 and thus d = 5.

However, the chaotic region is wider, as illustrated in the following ﬁgures.

FIGURE 10.4: Chaotic attractor in the two-sink problem

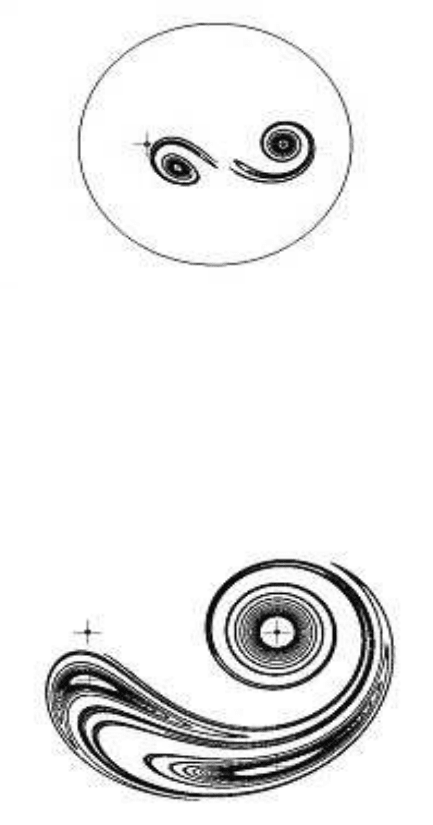
The chaotic attractor in Figure 10.4 illustrates the two-sink case for parameter

values a = 1, b = 0.8, c = π and d = 3. There are two main vortex forms

counterbalancing each other. The ﬁrst form is located at the right-hand-side sink at

(x, y) = (a, 0). The second vortex form is centred at (x, y) = (a+2ab cos φ, 2ab sin φ),

where φ = d/(4a

). The two main vortex forms can be separated when the parameter

d expressing the vortex strength is relatively small. Such a case is presented in Fig-

ure 10.5. The parameter d here is set to 1, while the other parameters remain the

same as in the previous example. The attractor is now completely separated into two

chaotic vortex forms (attractors).

Another possibility is to give high values to the parameter d expressing the vortex

strength. The value d = 2π leads to a more complicated vortex form, as presented

in Figure 10.6. There are three equilibrium points, for times t = 1, 2, 3. The ﬁrst of

these points is the centre of the right-hand-side sink.

One can also ﬁnd the form of the vortices in the case of three sinks located in an

equilateral triangle. The simulation of this situation is achieved by selecting a value

c =

2π

for the sink strength. The other parameters are b = 0.95, d = π and a = 5.

Figure 10.7(a) illustrates this case.

A form with four vortices is presented in Figure 10.7(b). This is achieved by as-

suming a special value, c =

2π

, for the parameter c, thus dividing the total circle in

four sectors. The positions of the four sinks are located on the corners of a square.

212 Chaotic Modelling and Simulation

FIGURE 10.5: Two distinct vortex forms (d = 1)

FIGURE 10.6: The chaotic attractor with strong vortex strength parameter

d = 2π

Chaotic Advection 213

The parameters selected for the simulation are b = 0.98, d = π and a = 5. Simi-

larly, a ﬁfth order vortex form results when c =

2π

and the other parameters remain

unchanged (Figure 10.7(c)).

(a) Third order (b) Fourth order (c) Fifth order

FIGURE 10.7: Vortex forms

10.4 Chaotic Forms without Space Contraction

Chaotic forms similar to those produced earlier in this chapter, but without any

space contraction, i.e. when b = 1, resulting in a Jacobian of J = 1, are of particular

interest. As there is no radial or space contraction, the ﬂow could be chaotic, but the

resulting chaotic attractors are not classiﬁed as main vortex forms.

Figure 10.8(a) illustrates the case where a = 1, b = 1, c = π and d = 1. The chaotic

form is symmetric. The axis y = 0 is the symmetry axis. A division of the main

chaotic form is starting. As the vortex strength parameter d is decreasing (d = 0.4 for

Figure 10.8(b) and d = 0.3 for Figure 10.8(c)) two distinct symmetric chaotic forms

arise. Figure 10.8(d) gives an enlargement of the right-hand-side chaotic attractor

produced when d = 0.3. Interesting chaotic details are present in this attractor.

10.5 Other Chaotic Forms

In the following simulation, we use the classical rotation-translation model with a

rotation angle expressed by an inverse function of the square of the radius r:

= c +

+ y