Skiadas C.H., Skiadas C. Chaotic Modelling and Simulation. Analysis of Chaotic Models, Attractors and Forms
Подождите немного. Документ загружается.

11.7 Chaotic forms of a simple rotation-translation model . . . . . . . . 233
11.8 Attractors and attracting points in rotation-translation model . . . . 234
11.9 A rotation image following a Contopoulos-Bozis paper (approach-
ing galaxies) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 235
11.10 Comparing chaotic forms: rotation-reflection . . . . . . . . . . . . 236
11.11 A rotation-translation chaotic image . . . . . . . . . . . . . . . . 237
11.12 Chaotic forms for low relativistic speeds . . . . . . . . . . . . . . 239
11.13 Relativistic rotation-translation forms for medium and high rela-
tivistic speeds . . . . . . . . . . . . . . . . . . . . . . . . . . . . 240
11.14 Relativistic rotation-translation forms for high relativistic speeds . 241
11.15 Non-relativistic chaotic images in the early period of a rotation-
translation process with b = 1 . . . . . . . . . . . . . . . . . . . . 242
11.16 Other relativistic chaotic images . . . . . . . . . . . . . . . . . . . 243
11.17 Various relativistic chaotic forms . . . . . . . . . . . . . . . . . . 243
11.18 Relativistic and initial chaotic images of a rotation-translation pro-
cess . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 244
11.19 Two galaxy-like chaotic images . . . . . . . . . . . . . . . . . . . 245
11.20 Other relativistic chaotic images . . . . . . . . . . . . . . . . . . . 246
11.21 A relativistic chaotic image when b = 0.9 . . . . . . . . . . . . . . 246
11.22 A relativistic chaotic image when b = 0.9 . . . . . . . . . . . . . . 247
11.23 A galactic-like cluster . . . . . . . . . . . . . . . . . . . . . . . . 247
11.24 Relativistic reflection-translation . . . . . . . . . . . . . . . . . . 249
11.25 Rotating disks . . . . . . . . . . . . . . . . . . . . . . . . . . . . 250
11.26 Two-armed galaxies . . . . . . . . . . . . . . . . . . . . . . . . . 252
11.27 Two-armed galaxies . . . . . . . . . . . . . . . . . . . . . . . . . 252
11.28 Rotating particles under the influence of an attracting mass . . . . 255
11.29 Box-like paths of a two-armed spiral galaxy . . . . . . . . . . . . 256
11.30 An asymptotically stable chaotic attractor . . . . . . . . . . . . . . 256
11.31 Rotation speed vs. radius r . . . . . . . . . . . . . . . . . . . . . 257
11.32 Two attracting masses and the disk of rotating particles at time t = 0 259
11.33 Rotating disks with two attracting masses . . . . . . . . . . . . . . 259
11.34 Rotating disks with two attracting masses over a long time . . . . . 260
11.35 Chaotic attractors in the case of two unequal symmetric attracting
masses . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 261
11.36 Rotating disc at early times . . . . . . . . . . . . . . . . . . . . . 262
11.37 Multi-arm images . . . . . . . . . . . . . . . . . . . . . . . . . . 263
11.38 The effect of two perpendicularly attracting masses . . . . . . . . 264
12.1 The original H
´
enon-Heiles (y, ˙y) diagram . . . . . . . . . . . . . . 268
12.2 (y, ˙y) diagrams for the H
´
enon-Heiles system . . . . . . . . . . . . 269
12.3 A discrete analogue to the H
´
enon-Heiles system (E = 1/12) . . . . 270
12.4 The discrete H
´
enon-Heiles model . . . . . . . . . . . . . . . . . . 271
12.5 Discrete analogues to the H
´
enon-Heiles system . . . . . . . . . . . 271
12.6 Chaotic paths in the H
´
enon-Heiles system . . . . . . . . . . . . . 272
12.7 The H
´
enon-Heiles system . . . . . . . . . . . . . . . . . . . . . . 273
12.8 Box-like orbits . . . . . . . . . . . . . . . . . . . . . . . . . . . . 274
12.9 A simple Hamiltonian: orbits and rotation forms at various times . 276
12.10 Orbits and rotation forms at time t = 1 . . . . . . . . . . . . . . . 278
12.11 Logarithmic potential: orbits and rotation forms at time t = 1 . . . 280
12.12 The Contopoulos system: orbits at resonance ratio 4/1 (left) and
2/3 (right) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 281
12.13 Another simple Hamiltonian system . . . . . . . . . . . . . . . . 282
13.1 Adding a sinusoidal forcing term to a two-dimensional system . . . 286
13.2 The effect of noise on three-dimensional models . . . . . . . . . . 287
13.3 The Lotka-Volterra system: limit cycle (upper image) and (t, x)
(heavy line) and the (t, y) (light line) graphs . . . . . . . . . . . . 289
13.4 The Lotka-Volterra system . . . . . . . . . . . . . . . . . . . . . 290
13.5 The pendulum and the (t, x) oscillations . . . . . . . . . . . . . . . 291
13.6 The (y, ˙y) curves of a special second order differential equation sys-
tem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 292
13.7 The dolphin attractor . . . . . . . . . . . . . . . . . . . . . . . . . 293
13.8 The ship and signature attractors . . . . . . . . . . . . . . . . . . 294
13.9 The Ushiki and Tinkerbell attractors . . . . . . . . . . . . . . . . 294

Contents
1 Introduction 1
1.1 Chaos in Differential Equations Systems . . . . . . . . . . . . . . 1
1.2 Chaos in Difference Equation Systems . . . . . . . . . . . . . . . 4
1.2.1 The logistic map . . . . . . . . . . . . . . . . . . . . . . 5
1.2.2 Delay models . . . . . . . . . . . . . . . . . . . . . . . . 6
1.2.3 The H
´
enon model . . . . . . . . . . . . . . . . . . . . . . 6
1.3 More Complex Structures . . . . . . . . . . . . . . . . . . . . . . 8
1.3.1 Three-dimensional and higher-dimensional models . . . . 8
1.3.2 Conservative systems . . . . . . . . . . . . . . . . . . . . 8
1.3.3 Rotations . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.3.4 Shape and form . . . . . . . . . . . . . . . . . . . . . . . 12
1.4 Chaos and the Universe . . . . . . . . . . . . . . . . . . . . . . . 14
1.4.1 Chaos in the solar system . . . . . . . . . . . . . . . . . . 14
1.4.2 Chaos in galaxies . . . . . . . . . . . . . . . . . . . . . . 19
1.4.3 Galactic-type potentials and the H
´
enon-Heiles system . . . 23
1.4.4 The Contopoulos system . . . . . . . . . . . . . . . . . . 25
1.5 Odds and Ends, and Milestones . . . . . . . . . . . . . . . . . . . 27
2 Models and Modelling 29
2.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
2.2 Model Construction . . . . . . . . . . . . . . . . . . . . . . . . . 30
2.2.1 Growth/decay models . . . . . . . . . . . . . . . . . . . . 30
2.3 Modelling Techniques . . . . . . . . . . . . . . . . . . . . . . . . 32
2.3.1 Series approximation . . . . . . . . . . . . . . . . . . . . 33
2.3.2 Empirical model formulation . . . . . . . . . . . . . . . . 36
2.3.3 The calculus of variations approach . . . . . . . . . . . . 38
2.3.4 The probabilistic-stochastic approach . . . . . . . . . . . 39
2.3.5 Delay growth functions . . . . . . . . . . . . . . . . . . . 40
2.4 Chaotic Analysis and Simulation . . . . . . . . . . . . . . . . . . 41
2.5 Deterministic, Stochastic and Chaotic Models . . . . . . . . . . . 42
3 The Logistic Model 47
3.1 The Logistic Map . . . . . . . . . . . . . . . . . . . . . . . . . . 47
3.1.1 Geometric analysis of the logistic . . . . . . . . . . . . . 47
3.1.2 Algebraic analysis of the logistic . . . . . . . . . . . . . . 51
3.2 The Bifurcation Diagram . . . . . . . . . . . . . . . . . . . . . . 58
3.3 Other Models with Similar Behaviour . . . . . . . . . . . . . . . 61
3.4 Models with Different Chaotic Behaviour . . . . . . . . . . . . . 62
3.5 The GRM1 Chaotic Model . . . . . . . . . . . . . . . . . . . . . 64
3.5.1 GRM1 and innovation diffusion modelling . . . . . . . . . 64
3.5.2 The generalized rational model . . . . . . . . . . . . . . . 66
3.5.3 Parameter estimation for the GRM1 model . . . . . . . . . 68
3.5.4 Illustrations . . . . . . . . . . . . . . . . . . . . . . . . . 69
3.6 Further Discussion . . . . . . . . . . . . . . . . . . . . . . . . . 71
4 The Delay Logistic Model 79
4.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
4.2 Delay Difference Models . . . . . . . . . . . . . . . . . . . . . . 79
4.2.1 Simple delay oscillation scheme . . . . . . . . . . . . . . 79
4.2.2 The delay logistic model . . . . . . . . . . . . . . . . . . 81
4.3 Time Delay Differential Equations . . . . . . . . . . . . . . . . . 82
4.4 A More Complicated Delay Model . . . . . . . . . . . . . . . . . 84
4.5 A Delay Differential Logistic Analogue . . . . . . . . . . . . . . 86
4.6 Other Delay Logistic Models . . . . . . . . . . . . . . . . . . . . 86
4.7 Model Behaviour for Large Delays . . . . . . . . . . . . . . . . . 89
4.8 Another Delay Logistic Model . . . . . . . . . . . . . . . . . . . 91
5 The H
´
enon Model 99
5.1 Global Period Doubling Bifurcations in the H
´
enon Map . . . . . . 99
5.1.1 Period doubling bifurcations when b = −1 . . . . . . . . . 100
5.1.2 Period doubling bifurcations when b = 1 . . . . . . . . . . 101
5.2 The Cosine-H
´
enon Model . . . . . . . . . . . . . . . . . . . . . . 101
5.3 An Example of Bifurcation and Period Doubling . . . . . . . . . . 103
5.4 A Differential Equation Analogue . . . . . . . . . . . . . . . . . 103
5.5 Variants of the H
´
enon Delay Difference Equation . . . . . . . . . 104
5.5.1 The third-order delay model . . . . . . . . . . . . . . . . 104
5.5.2 Second-order delay models . . . . . . . . . . . . . . . . . 105
5.5.3 First-order delay variants . . . . . . . . . . . . . . . . . . 107
5.5.4 Exponential variants . . . . . . . . . . . . . . . . . . . . 108
5.6 Variants of the H
´
enon System Equations . . . . . . . . . . . . . . 109
5.7 The Holmes and Sine Delay Models . . . . . . . . . . . . . . . . 110
5.7.1 The Holmes model . . . . . . . . . . . . . . . . . . . . . 110
5.7.2 The sine delay model . . . . . . . . . . . . . . . . . . . . 111
6 Three-Dimensional and Higher-Dimensional Models 117
6.1 Equilibrium Points and Characteristic Matrices . . . . . . . . . . 117
6.2 The Lotka-Volterra Model . . . . . . . . . . . . . . . . . . . . . . 118
6.3 The Arneodo Model . . . . . . . . . . . . . . . . . . . . . . . . . 119
6.4 An Autocatalytic Attractor . . . . . . . . . . . . . . . . . . . . . 121
6.5 A Four-Dimensional Autocatalytic Attractor . . . . . . . . . . . . 122
6.6 The R
¨
ossler Model . . . . . . . . . . . . . . . . . . . . . . . . . 123
6.6.1 A variant of the R
¨
ossler model . . . . . . . . . . . . . . . 124
6.6.2 Introducing rotation into the R
¨
ossler model . . . . . . . . 127
6.7 The Lorenz Model . . . . . . . . . . . . . . . . . . . . . . . . . . 129
6.7.1 The modified Lorenz model . . . . . . . . . . . . . . . . 131
7 Non-Chaotic Systems 135
7.1 Conservative Systems . . . . . . . . . . . . . . . . . . . . . . . . 135
7.1.1 The simplest conservative system . . . . . . . . . . . . . 137
7.1.2 Equilibrium points in Hamiltonian systems . . . . . . . . 138
7.2 Linear Systems . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
7.2.1 Transformations on linear systems . . . . . . . . . . . . . 140
7.2.2 Qualitative behaviour at equilibrium points . . . . . . . . 142
7.3 Egg-Shaped Forms . . . . . . . . . . . . . . . . . . . . . . . . . 144
7.3.1 A simple egg-shaped form . . . . . . . . . . . . . . . . . 144
7.3.2 A double egg-shaped form . . . . . . . . . . . . . . . . . 145
7.3.3 A double egg-shaped form with an envelope . . . . . . . . 146
7.4 Symmetric Forms . . . . . . . . . . . . . . . . . . . . . . . . . . 148
7.5 More Complex Forms . . . . . . . . . . . . . . . . . . . . . . . . 150
7.6 Higher-Order Forms . . . . . . . . . . . . . . . . . . . . . . . . . 153
8 Rotations 157
8.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157
8.2 A Simple Rotation-Translation System of Differential Equations . 158
8.3 A Discrete Rotation-Translation Model . . . . . . . . . . . . . . . 163
8.4 A General Rotation-Translation Model . . . . . . . . . . . . . . . 169
8.5 Rotating Particles inside the Egg-Shaped Form . . . . . . . . . . . 171
8.6 Rotations Following an Inverse Square Law . . . . . . . . . . . . 173
9 Shape and Form 179
9.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 179
9.1.1 Symmetry and plane isometries . . . . . . . . . . . . . . . 180
9.2 Isometries in Modelling . . . . . . . . . . . . . . . . . . . . . . . 184
9.2.1 Two-dimensional rotation . . . . . . . . . . . . . . . . . . 184
9.3 Reflection and Translation . . . . . . . . . . . . . . . . . . . . . 186
9.3.1 Space contraction . . . . . . . . . . . . . . . . . . . . . . 186
9.4 Application in the Ikeda Attractor . . . . . . . . . . . . . . . . . . 187
9.5 Chaotic Attractors and Rotation-Reflection . . . . . . . . . . . . . 188
9.6 Experimenting with Rotation and Reflection . . . . . . . . . . . . 191
9.6.1 The effect of space contraction on rotation-translation . . . 191
9.6.2 The effect of space contraction and change of reflection
angle on translation-reflection . . . . . . . . . . . . . . . 192
9.6.3 Complicated rotation angle forms . . . . . . . . . . . . . 193
9.6.4 Comparing rotation-reflection . . . . . . . . . . . . . . . 194
9.6.5 A simple rotation-translation model . . . . . . . . . . . . 196
9.7 Chaotic Circular Forms . . . . . . . . . . . . . . . . . . . . . . . 196
9.8 Further Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . 200
9.8.1 The space contraction rotation-translation case . . . . . . 202
10 Chaotic Advection 205
10.1 The Sink Problem . . . . . . . . . . . . . . . . . . . . . . . . . . 205
10.1.1 Central sink . . . . . . . . . . . . . . . . . . . . . . . . . 205
10.1.2 The contraction process . . . . . . . . . . . . . . . . . . . 207
10.2 Non-Central Sink . . . . . . . . . . . . . . . . . . . . . . . . . . 207
10.3 Two Symmetric Sinks . . . . . . . . . . . . . . . . . . . . . . . . 208
10.3.1 Aref’s blinking vortex system . . . . . . . . . . . . . . . 208
10.4 Chaotic Forms without Space Contraction . . . . . . . . . . . . . 213
10.5 Other Chaotic Forms . . . . . . . . . . . . . . . . . . . . . . . . 213
10.6 Complex Sinusoidal Rotation Angle . . . . . . . . . . . . . . . . 216
10.7 A Special Rotation-Translation Model . . . . . . . . . . . . . . . 219
10.8 Other Rotation-Translation Models . . . . . . . . . . . . . . . . . 219
10.8.1 Elliptic rotation-translation . . . . . . . . . . . . . . . . . 219
10.8.2 Rotation-translation with special rotation angle . . . . . . 220
11 Chaos in Galaxies and Related Simulations 223
11.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 223
11.2 Chaos in the Solar System . . . . . . . . . . . . . . . . . . . . . 225
11.3 Galaxy Models and Modelling . . . . . . . . . . . . . . . . . . . 228
11.3.1 A special rotation-translation image . . . . . . . . . . . . 234
11.4 Rotation-Reflection . . . . . . . . . . . . . . . . . . . . . . . . . 235
11.5 Relativity in Rotation-Translation Systems . . . . . . . . . . . . . 236
11.6 Other Relativistic Forms . . . . . . . . . . . . . . . . . . . . . . 241
11.7 Galactic Clusters . . . . . . . . . . . . . . . . . . . . . . . . . . 247
11.8 Relativistic Reflection-Translation . . . . . . . . . . . . . . . . . 248
11.9 Rotating Disks of Particles . . . . . . . . . . . . . . . . . . . . . 248
11.9.1 A circular rotating disk . . . . . . . . . . . . . . . . . . . 248
11.9.2 The rotating ellipsoid . . . . . . . . . . . . . . . . . . . . 250
11.10 Rotating Particles under Distant Attracting Masses . . . . . . . . . 253
11.10.1 One attracting mass . . . . . . . . . . . . . . . . . . . . . 253
11.10.2 The area of the chaotic region in galaxy simulations . . . . 255
11.10.3 The speed of particles . . . . . . . . . . . . . . . . . . . . 257
11.11 Two Equal Attracting Masses in Opposite Directions . . . . . . . 258
11.11.1 Symmetric unequal attracting masses . . . . . . . . . . . 260
11.12 Two Attracting Equal Nonsymmetric Masses . . . . . . . . . . . . 263
12 Galactic-Type Potentials and the H
´
enon-Heiles System 267
12.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 267
12.2 The H
´
enon-Heiles System . . . . . . . . . . . . . . . . . . . . . 268
12.3 Discrete Analogues to the H
´
enon-Heiles System . . . . . . . . . . 270
12.4 Paths of Particles in the H
´
enon-Heiles System . . . . . . . . . . . 272
12.5 Other Forms for the Hamiltonian . . . . . . . . . . . . . . . . . . 273
12.6 The Simplest Form for the Hamiltonian . . . . . . . . . . . . . . 275
12.7 Gravitational Attraction . . . . . . . . . . . . . . . . . . . . . . . 275
12.8 A Logarithmic Potential . . . . . . . . . . . . . . . . . . . . . . . 279
12.9 Hamiltonians with a Galactic Type Potential: The Contopoulos
System . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 279
12.10 Another Simple Hamiltonian System . . . . . . . . . . . . . . . . 281
13 Odds and Ends 285
13.1 Forced Nonlinear Oscillators . . . . . . . . . . . . . . . . . . . . 285
13.2 The Effect of Noise in Three-Dimensional Models . . . . . . . . . 285
13.3 The Lotka-Volterra Theory for the Growth of Two Conflicting
Populations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 288
13.4 The Pendulum . . . . . . . . . . . . . . . . . . . . . . . . . . . . 290
13.5 A Special Second-Order Differential Equation . . . . . . . . . . . 292
13.6 Other Patterns and Chaotic Forms . . . . . . . . . . . . . . . . . 292
14 Milestones 297
References 303
Chapter 1
Introduction
1.1 Chaos in Differential Equations Systems
Four centuries ago, Newton and other scientists introduced the idea of determin-
ism in the mathematical representation of the real world. As a result, future events
in nature could be explained using knowledge of the past. The movements of stel-
lar bodies were assumed to follow predetermined paths according to laws that were
known or had to be discovered by the scientific community. The theory of deter-
minism also had theoretical support from philosophy and other scientific fields. It
would be difficult to say that determinism, as a general idea, can solve all problems
in nature. The scientists of the last few centuries followed this theory in order to
find rational routes in the construction of models. It was essential to simplify our
description of the world first, and only then to solve fundamental problems, instead
of entering into obscure paths of uncertainty and later on Chaos.
How then does one introduce a theory that goes against the perfect world of New-
tonian dynamics? Our solar system has been rotating for millions of years, and the
experience of the last centuries was in favor of determinism. The sun continues to
rise every day, the moon follows a four-week period, the stars of Ursa Major are
found every year in predetermined places. How and why could this perfect deter-
ministic world lose this certainty and lead a chaotic existence?
It was not easy to convince the scientific community to introduce uncertainty into
this deterministic world and accept chaotic theories. However, advances in applied
mathematics made this transition easier. At the end of the nineteenth century, the
Runge-Kutta method for numerical solutions to differential equations dramatically
improved our ability to get more accurate solutions for numerous models. It was a
real milestone in applied mathematics, especially for the study of highly non-linear
problems, for which the earlier method by Euler was not very accurate.
Following the introduction of the Runge-Kutta method, the paths traversed by a
stellar body could now be estimated quite efficiently. Although this method was
still quite laborious at those early days, it gave new directions in the way scientists
addressed various problems. Theory and practice could now equally benefit each
other.
It is no surprise that this change influenced even the French school, traditionally
the most theoretical of all, especially in mathematics and physics. Henri Poincar
´
e,
one of the most prominent scientists in 19th century France, tried to resolve the
1

2 Chaotic Modelling and Simulation
famous three-body problem in a contest proposed by the King of Norway (Poincar
´
e,
1890b, 1892). Although he succeeded in solving a special case of this problem,
namely the movement of a small mass around two larger masses revolving in two
dimensions, he noticed that the orbits of three bodies moving under a central force
due to gravity are quite complicated and can change drastically under small changes
of the initial conditions.
Nowadays we know that to solve this problem we need a set of more than three
coupled differential equations, and the paths of the solutions have a chaotic charac-
ter. Poincar
´
e tried to determine solutions to the restricted three-body problem, when
one mass is very small relative to the other two. He understood that, even in this
simple case, the motion had still a very complicated form. He tried to explain the
phenomenon more generally and to establish a theory describing the chaotic paths of
the solutions to a system of differential equations: The three-dimensional solutions
to a system of non-linear differential equations could be chaotic. In stark contrast,
the two-dimensional paths do not exhibit a chaotic behaviour, as follows from the
famous Poincar
´
e-Bendixson theorem: Chaos cannot occur in a two-dimensional au-
tonomous system.
To elaborate a bit, consider the two-dimensional autonomous system (1.1):
˙x = f (x, y)
˙y = g(x, y)
(1.1)
where ˙x and ˙y are the first time derivatives. The system (1.1) can take the form of a
two-dimensional equation for x and y:
dy
dx
=
g(x, y)
f (x, y)
(1.2)
and we can find phase paths in the plane describing the motion, directly from 1.2.
Assuming that we have determined the equilibrium points at which both f (x, y) = 0
and g(x, y) = 0, the Poincar
´
e-Bendixson theorem says that a phase path will either:
a) terminate at an equilibrium point,
b) return to the original point, resulting in a closed path, or
c) approach a limit cycle.
Hence, there are no chaotic solutions. The system of differential equations (1.3)
illustrates all three cases:
˙x = −y(y − a)(y − b)
˙y = x(x − a)(x − b)
(1.3)
The resulting differential equation for x, y is:
dy
dx
= −
x(x − a)(x − b)
y(y − a)(y − b)
Introduction 3
This equation can be easily integrated, resulting in the solution:
x
4
+ y
4
4
− (a + b)
x
3
+ y
3
3
+ ab
x
2
+ y
2
2
= h
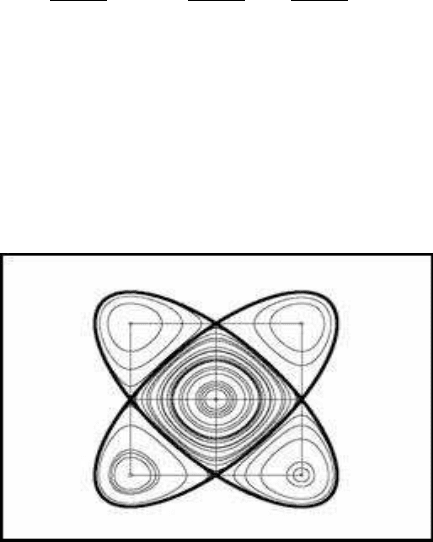
where h is the constant of integration. The paths, with parameters equal to a = 0.8
and b = 0.3, are illustrated in Figure 1.1. There are nine equilibrium points, four
at centres four corners, four in the sides, and one in the middle of the figure. The
more complex paths pass from the four unstable equilibrium points at the sides. Such
systems, not chaotic in themselves but nonetheless not without interest, are further
discussed in Chapter 7.
FIGURE 1.1: The (x, y) diagram
On the other hand, the simplest three-dimensional non-linear system of differential
equations, the R
¨
ossler model (R
¨
ossler, 1976d)
˙x = −y − z
˙y = x + ey
˙z = f + xz − mz
(1.4)
easily produces chaotic paths for appropriate values of the parameters.
The R
¨
ossler system has only one non-linear term, in the last equation. However,
when the parameters have values e = f = 0.2 and m = 5.7, chaotic paths appear with
the form presented in Figure 1.2(a). The R
¨
ossler system, along with other interesting
three-dimensional systems, is examined in greater detail in Chapter 6.
