Skiadas C.H., Skiadas C. Chaotic Modelling and Simulation. Analysis of Chaotic Models, Attractors and Forms

Подождите немного. Документ загружается.

54 Chaotic Modelling and Simulation

(a) b = 2.7 (b) b = 3

FIGURE 3.7: The logistic map, b ≤ 3

(a) b = 3.43 (b) b = 1 +

√

FIGURE 3.8: The logistic map, b > 3

The Logistic Model 55

which has three real roots. Two of them are acceptable, b = 2 and b = 1 +

√

5. These

are the same points where the order-2 curve meets the main diagonal.

Figure 3.8(b)

illustrates the case where b = 1 +

√

5, with x

= 0.25.

The period-4 bifurcation appears in Figure 3.9. For better presentation, and in or-

der to locate the characteristic points, we introduce the inverse (x

t+3

, x

) and (x

, x

t+4

)

diagrams. The 4-point orbit can be thought of either as the points of intersection of

the (x

, x

t+4

) diagram (purple line) with the line y = x, or as the points of intersection

of the x

t+3

, x

diagram (blue line) with the curve y = f (x). The parameter b is con-

strained in the range 1 +

√

6 < b < 3.5440903 ···. There are 4 characteristic values

for x.

FIGURE 3.9: Order-4 bifurcation of the logistic map; real time and phase

space diagrams

The right of Figure 3.9 is the real time diagram (x

, t), whereas the left is the phase

space diagram (x

, x

t+4

). In the real time diagram the order-4 oscillations appear. The

values of x

, after enough time has elapsed, oscillate between theses four limiting

levels.

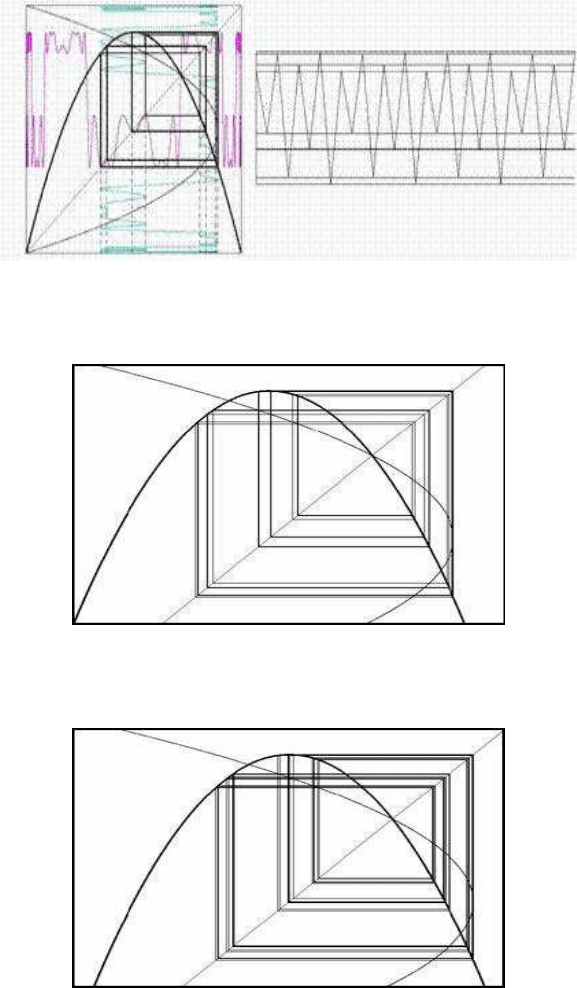
When 3.5440903 ··· < b < 3.5644073 ··· the period-8 bifurcation appears. Fig-

ure 3.10 illustrates this case. The chaotic parameter is b = 3.5644, and the inverse

function is given by the (x

t+7

, x

) diagram. The order-8 logistic bifurcation is ex-

pressed by the (x

, x

t+8

) diagram. A real time diagram of the chaotic oscillations

appears on the right of Figure 3.10.

The period-16 bifurcation is illustrated in Figure 3.11. The range covered by the

parameter b is 3.5644073 ··· < b < 3.5687594 ···. For the application we set b =

3.5687594 ···. Figure 3.12 presents the period-32 bifurcation (b = 3.56969). The

range for b is 3.5687594 ··· < b < 3.5696916 ···.

Since if y = f (x), then asking for f (y) = x is the same as asking for f ( f (x)) = x.

56 Chaotic Modelling and Simulation

FIGURE 3.10: Order-8 bifurcation of the logistic map; real time and phase

space diagrams

FIGURE 3.11: Order-16 bifurcation and real time and phase space diagrams

of the logistic

FIGURE 3.12: Order-32 bifurcation and real time and phase space diagrams

of the logistic

The Logistic Model 57

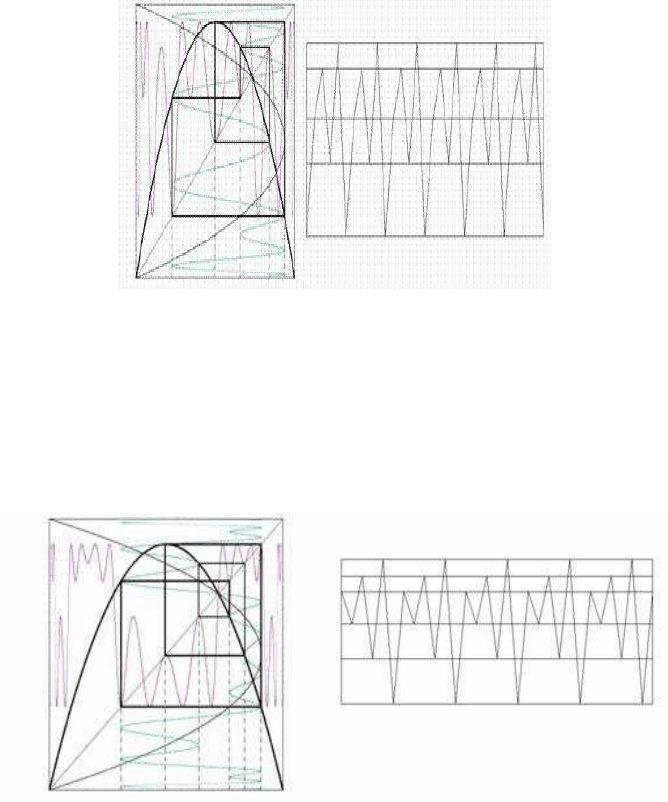
The order-5 bifurcation appears in Figure 3.13. The inverse function is given by

the (x

t+4

, x

) diagram. The order-5 logistic bifurcation is expressed by the (x

, x

t+5

)

diagram. The chaotic oscillations appear in the real time diagram (right).

FIGURE 3.13: The order-5 bifurcation and real time and phase space diagrams

The order-6 bifurcation appears in Figure 3.14 (b = 3.6267). The inverse function

is here given with the (x

t+5

, x

) diagram. The order-6 logistic bifurcation is expressed

by the (x

, x

t+6

) diagram. The chaotic oscillations appear in the real time diagram

(right).

FIGURE 3.14: The order-6 bifurcation and real time and phase space diagrams

58 Chaotic Modelling and Simulation

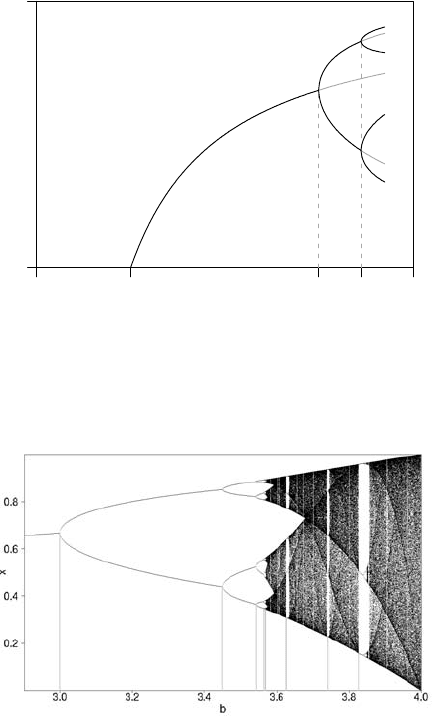
3.2 The Bifurcation Diagram

The period doubling and other properties of the logistic map are presented in the

so-called bifurcation diagram. This is a two-dimensional graph (b, x

) formed as

follows: For each value of the chaotic parameter b, the values of x

that form the

stable orbit are plotted. Figure 3.15(a) shows how the bifurcation diagram looks for

b < 3.5. For 0 < b < 1, there is only one ﬁxed point, at x = 0. For 1 < b < 3, the

ﬁxed point is x = 1 −

. At b = 3, this splits up into the order-two orbit, which at

3.449 becomes unstable and splits up into an order-4 orbit and so on. The greyed out

lines show the values that these orbits would have had if they were still stable.

The full bifurcation diagram for the logistic map appears in Figure 3.15(b). The

ﬁrst bifurcation point is located at



b = 3, x = 1 −



, and the next two at b ≈ 3.4495,

the next four at b ≈ 3.54409 and so on, according to the theory. These points can

be calculated by solving the appropriate equation of the form f

(x) = x, though this

becomes exceedingly diﬃcult as n increases. The construction of the bifurcation

diagram typically follows these steps:

1. Break the range of b ([0, 4]) into small intervals.

2. For each interval, choose a b in that interval (say the left end-point), and per-

form repeated applications of the iterative process x

n+1

= f (x

) until stability

is achieved. At this point, the desired values x

will be determined.

3. Move on to the next value of b. Use the previously found stable x values as

starting points for the iteration process, to achieve stability much quicker.

The characteristic values of the parameter b at each bifurcation stage follow the

Feigenbaum law. According to this law the sequence of period doubling, presented

in the above ﬁgure by a bifurcation tree, is due to a quantitative convergence of the

parameter b, which tends to a universal parameter δ = 4.6692016 ···. This parameter

is given by the expression

δ = lim

i→∞

i−1

− b

i+1

The behaviour of the system can be understood better by considering a scaled

version. More generally, if we consider a system

n+1

= f (x

)

then we consider the function:

g(x) = lim

n→∞

(0)



x f

(0)



Then, under some mild conditions on the map f , g satisﬁes the universal equation:

g(αx) = −αg



(

−x

)



(3.8)

The Logistic Model 59

0 1 3 3.449 4

(a) The ﬁrst two bifurcations

(b) The whole diagram

FIGURE 3.15: The bifurcation diagram of the logistic

60 Chaotic Modelling and Simulation

Here α is the second Feigenbaum constant, related to the ratio of the width between

the prongs in a bifurcation, relative to the width in the previous bifurcation.

The function g can be approximated by a ﬁnite polynomial, and from that it is

possible to estimate α = 2.50290787 ···, with the normalisation convention g(0) =

1 (Lanford, 1982a).

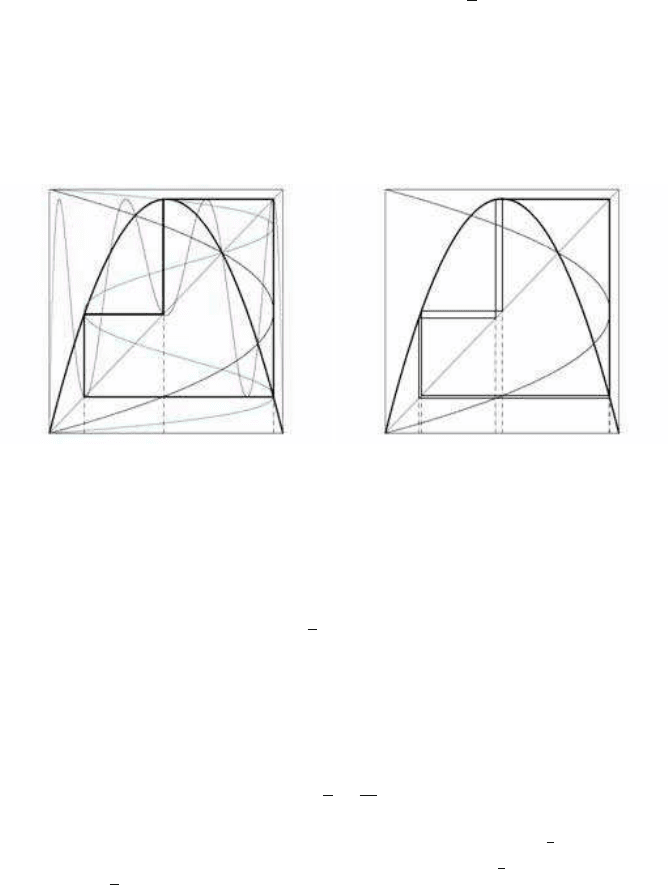
Other interesting properties arising from the bifurcation diagram come from ob-

serving the three “windows” which appear in a range of characteristic values of the

parameter b around b

= 3.627, b

= 3.74 and b

= 1 +

√

8. These values of b give

sixth, ﬁfth and third order bifurcations respectively, and the related period doubling

bifurcations lead to 12, 10 and 6 and higher order bifurcation forms. The period-3

bifurcation can be seen in Figure 3.16(a). In Figure 3.16(b) the order 2 × 3 = 6

bifurcation is illustrated (b = 3.845).

(a) Order-3 bifurcation (b) Order 2 ×3 bifurcation

FIGURE 3.16: Order-3 bifurcations

A change of variables

z =

b(1 − 2x)

results in the following expression for the logistic equation:

t+1

= z

+ c

where

c =

−

From this point of view, the ﬁrst period doubling occurs at c = −

, which corre-

sponds to b = 3. The second period doubling occurs at c = −

, which corresponds

to b = 1 +

√

6, while the period-3 solutions appear at a saddle-node bifurcation at

The Logistic Model 61

c = −

, corresponding to b = 1 +

√

8. An illustration of the period-3 bifurcation

using the z-form of the logistic equation appears in Figure 3.17.

FIGURE 3.17: The order-3 bifurcation

3.3 Other Models with Similar Behaviour

Functions with varying equation forms show chaotic behaviour similar to the lo-

gistic. One of them is the sinusoidal map, with equation

t+1

= b sin(x

)

where b is restricted to the interval 0 < b ≤ π. A more convenient form is:

t+1

= b sin(πx

)

Now the interval for the parameter is 0 < b ≤ 1.

Another model is the Gompertz type model (Gompertz, 1825):

t+1

= −bx

ln(x

)

where 0 < b ≤ e = 2.71829 ···.

Another model was proposed by May (May, 1972, 1974, 1976) to describe the

population growth of a single species population, which is regulated by an epidemic

disease at high density:

t+1

= x

r(1−x

)

The chaotic behaviour of this model is similar to that of the logistic model, as

illustrated by the bifurcation diagram (Figure 3.18, right). The order-4 bifurcation is

presented on the left of Figure 3.18 (r = 2.6).

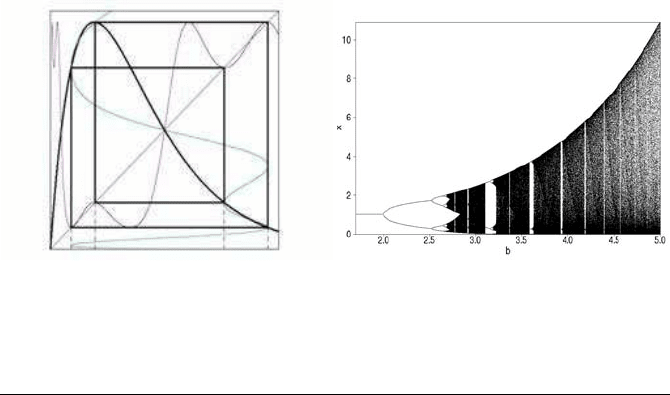
62 Chaotic Modelling and Simulation

FIGURE 3.18: The May model: an order-4 bifurcation (left) and the

bifurcation diagram (right)

3.4 Models with Diﬀerent Chaotic Behaviour

Some Gaussian models show special chaotic behaviour, mainly due to the quadratic

exponent in the equations of these models. A simple Gaussian equation is:

t+1

= b + e

−ax

The bifurcation diagram for a = 4 and −1 < b < 1 is shown on the left of

Figure 3.19(a). The model has two period doubling bifurcations, and then it returns

to the original state in a reverse order. A further increase in the parameter a of the

quadratic term, a = 7.5, gives a full sequence of period doubling bifurcations and

order-3 saddle-node bifurcations (Figure 3.19(b), right).

When the parameter a takes higher values, the chaotic behaviour of the model

changes radically. This is presented in Figure 3.20 (a = 17, −1.2 < b < 1).

A rich bifurcation diagram appears when the Gaussian model is combined with

the logistic to form the G-L model:

t+1

= b − x

(1 − x

) + e

−ax

When a = 7.5, the bifurcation diagram in the range −1.1 < b < 0.7 has the

form illustrated in Figure 3.21. There are two main bifurcation regions, with period

doubling bifurcations and order-3 and order-5 saddle-node bifurcations. The order-5

bifurcation is presented in Figure 3.22(a) (a = 7.5, b = 0.19).

Figure 3.22(b) illustrates a perfect order-12 circle (a = 7.5, b = 0.11).

The Logistic Model 63

(a) a = 4 (b) a = 7.5

FIGURE 3.19: Bifurcation diagrams of the Gaussian model

FIGURE 3.20: Bifurcation diagram of the Gaussian model (a = 17)

FIGURE 3.21: Bifurcation diagram of the G-L model