Skiadas C.H., Skiadas C. Chaotic Modelling and Simulation. Analysis of Chaotic Models, Attractors and Forms

Подождите немного. Документ загружается.

194 Chaotic Modelling and Simulation

A simpler form is produced by assuming that in the function for the rotation angle

the parameter c is 0. The resulting chaotic system provides an attractor expressing

ﬂows appearing in the mixing of ﬂuids but, also, in other rotation-translation systems.

The parameters in Figure 9.16 were a = 1, b = 0.87, d = 1 and m = 3.1.

FIGURE 9.16: The eﬀect of a complicated rotation angle on chaotic attractors

A two-piece chaotic attractor is formed by using a rotation-translation formula

with a special rotation angle. The rotation angle has a constant term denoted by c and

a varying term related to a transformed distance. The model is a space contracting

one (b = 0.9). It also has a slightly diﬀerent form for the rotation-translation

n+1

= a + b(x

cos θ

− y

sin θ

)

n+1

= −a + b(x

sin θ

+ y

cos θ

)

(9.15)

where the rotation angle is

= c +



x−a





y+a



The other parameters were set to a = 9, c = a and d = 6. The two-piece chaotic

attractor is presented in Figure 9.17(a).

9.6.4 Comparing rotation-reﬂection

Figure 9.17(b) illustrates a two-piece chaotic attractor, resulting from a set of equa-

tions expressing rotation and translation without space contraction (b = 1). The

rotation angle is a function of r, that is

= c +

+ y

Shape and Form 195

(a) With space contraction (b) Without space contraction

FIGURE 9.17: Two-piece chaotic attractors

The process shows how an original rotating disk of particles can form two distinct

symmetric chaotic forms. The parameters were set to a = 37, c = 2.85 and d = 15.5.

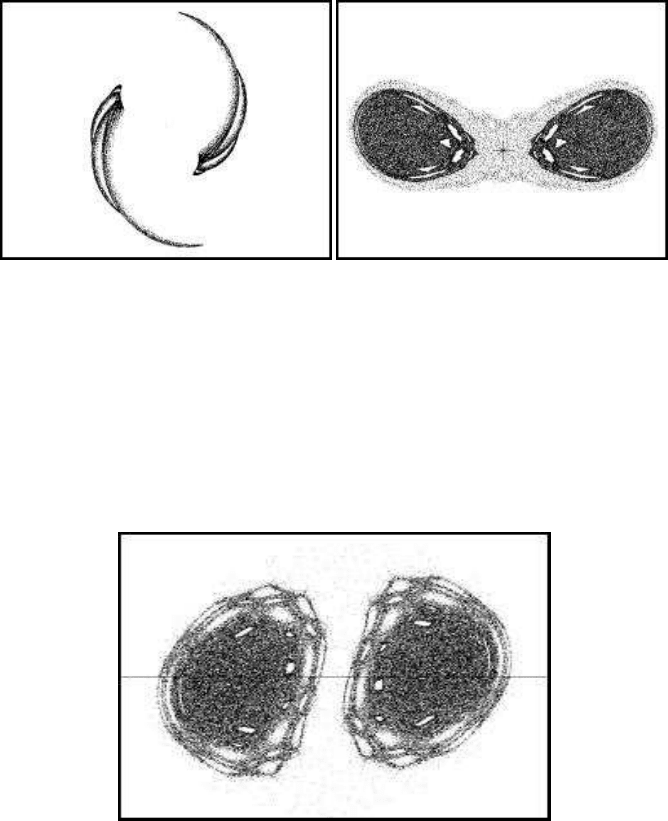
FIGURE 9.18: Reﬂection: a two-piece chaotic attractor

The images presented in Figure 9.18 are the reﬂection analogue of this system.

The reﬂection-translation equations without space contraction (b = 1) are used. The

reﬂection angle (θ

re f

) is as in the previous rotation-translation case but it is related

to the rotation angle (θ

rot

) by the relation θ

re f

= 2θ

rot

. When the parameters take the

values a = 80, c = 5 and d = −20, the reﬂection-translation model provides two

objects with mirror symmetry, as illustrated in Figure 9.18.

196 Chaotic Modelling and Simulation

9.6.5 A simple rotation-translation model

FIGURE 9.19: A simple area preserving rotation-translation model

A simple space preserving (b = 1) rotation-translation model with a rotation angle,

varying according to the square of the distance r from the origin (θ

= c(x

+ y

) =

), also gives an interesting rotation-translation image, illustrated in Figure 9.19.

There is an island with equilibrium points achieved when (x

n+1

= x

, y

n+1

= y

centred on the symmetry axis (x = a/2), and four symmetric islands (in two pairs)

with equilibrium points that follow the rule x

n+4

= x

and y

n+4

= y

. The parameters

were set to a = 1 and c = 0.65.

9.7 Chaotic Circular Forms

The study of a rotation process in which the rotating particles move at circular

or other paths from the centre following a speciﬁc formula is of particular interest.

The simulations arising out of these cases start by forming concentric circles with

diﬀerent particle density and can lead to more complicated forms, depending on the

selected set of non-linear functions. The iterations follow the simple scheme:

= r

cos θ

= r

sin θ

(9.16)

where θ

increases in a constant way:

n+1

= θ

+ θ

Shape and Form 197

Depending on the iterative scheme for the radius r

, interesting patterns arise, along

with chaotic behaviour. As a simple example, consider the iterative formula:

n+1

= b −

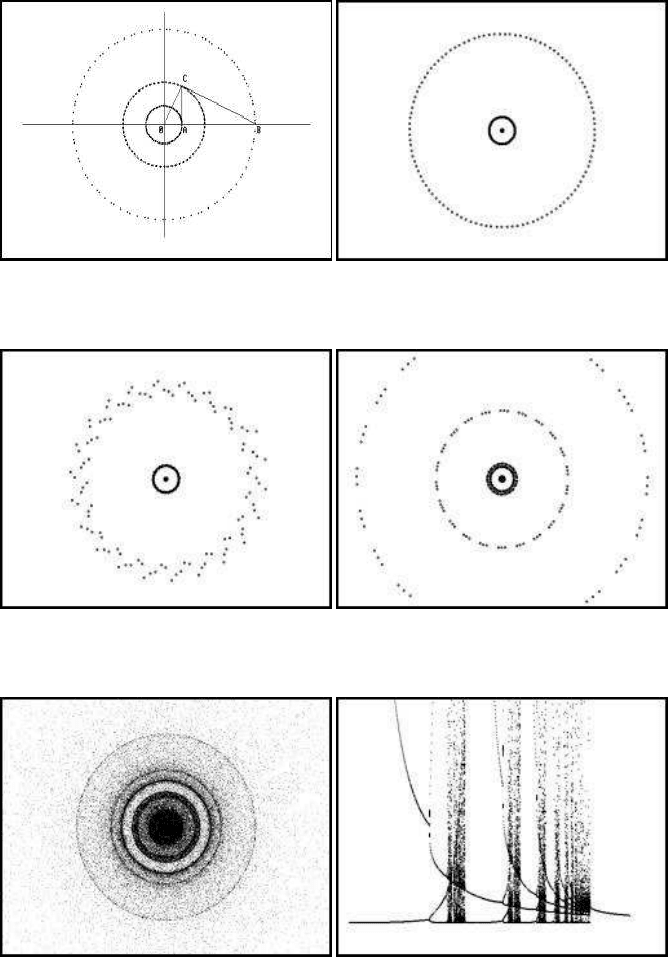
The (a, r) bifurcation diagram for this model is shown in Figure 9.20(a). Second,

third, fourth and higher order bifurcations appear. The parameter b is set to 2.4,

while the parameter a varies in 1.2 < a < 6.9.

Figure 9.20(b) illustrates the bifurcation diagram (a, r) of the model expressed by

the formula:

n+1

= b −

The parameter b is set to 2.4, while the parameter a varies in 0.2 < a < 60.

Figure 9.20(c) illustrates the (a, r) bifurcation diagram of the model:

n+1

= b −

The parameter b is set to 2.4 and the parameter a varies in 0.2 < a < 60.

The development of the theory of rotation with varying rotation distance from the

origin, or with varying rotation angle related to the distance r =

+ y

, is partly

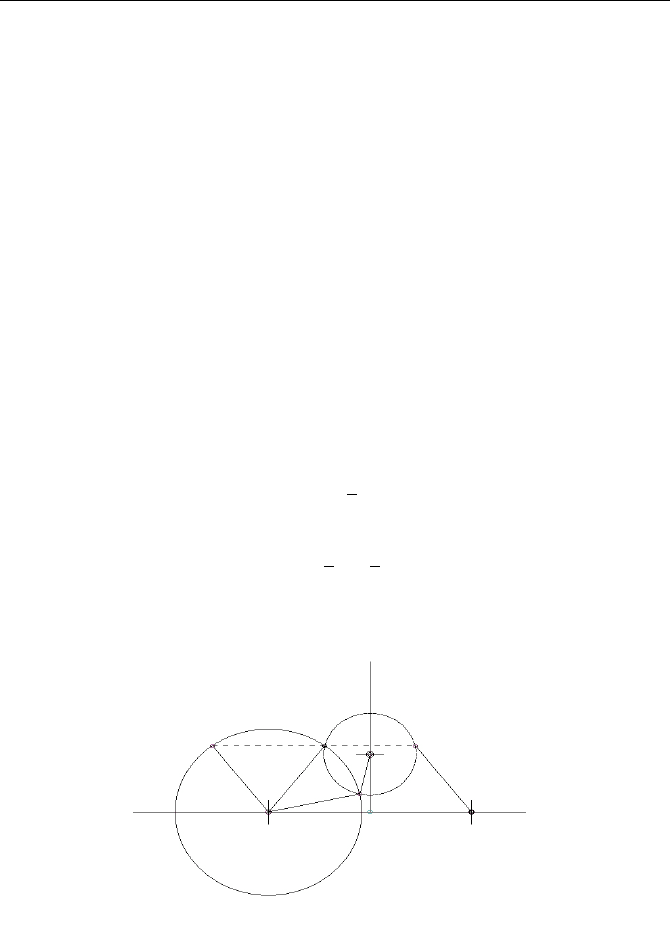
explained by using Figure 9.21(a), where OC = r.

A very interesting rotation scheme is presented in Figure 9.21(b). There is only

one parameter b = 1.195. The radius r follows an inverse square law:

n+1

− b)

(9.17)

Chaotic behaviour appears when the parameter b varies. A small change in b leads

to the onset of chaos. For b = 1.204, the bifurcation has already started to divide the

outer ring in two rings (Figure 9.21(c)). The bifurcation process leads to chaos when

higher values for b are selected.

In Figure 9.21(d), there appear the distinct circles. By giving to the chaotic

parameter b the value 1.255, the particles are distributed in a particular chaotic

way. There are cyclical regions with higher or lower densities, as presented in Fig-

ure 9.21(e).

Figure 9.21(f) presents the bifurcation diagram (b, r) for the model (9.17). The

parameter b varies between 0 < b < 2.2. The model gives two values for r in the

region of 0 < b < 0.629 ···. At 0.629 ···, as b increases, a second bifurcation starts,

leading to a chaotic region. At the end of this region, three values for r appear,

making up a new chaotic region, then four values, and so on until a totally chaotic

region at 1.88 ···.

198 Chaotic Modelling and Simulation

(a) r

n+1

= b −

(b) r

n+1

= b −

n+1

= b −

FIGURE 9.20: Bifurcation diagrams

Shape and Form 199

(a) The geometry of circular chaotic forms (b) A circular form

(e) b = 1.255 (f) Bifurcation diagram for the model (9.17)

FIGURE 9.21: Circular chaotic forms

200 Chaotic Modelling and Simulation

9.8 Further Analysis

Consider a rotation-translation case expressed by the relations

n+1

= a + x

cos θ

− y

sin θ

n+1

= x

sin θ

+ y

cos θ

(9.18)

or in the equivalent form

n+1

= a + z

iθ

where z

= x

+ iy

This map is symmetric with the line x = a/2 as the axis of symmetry. This is easily

demonstrated if we consider the ﬁxed points, i.e. solutions of the form z

n+1

= z

= z.

In other words, when (x

n+1

, y

n+1

) = (x

, y

) = (x, y). Now the following relation

holds:

|z − a| = |z|

(x − a)

+ y

= x

+ y

and, ﬁnally,

x =

whereas for y

y =

cot

FIGURE 9.22: Geometric analogue of rotation-translation (θ = 2)

A geometric analogue of this rotation-translation case is illustrated in Figure 9.22

where the translation parameter is a = 2, the rotation angle is θ = 2 and the initial

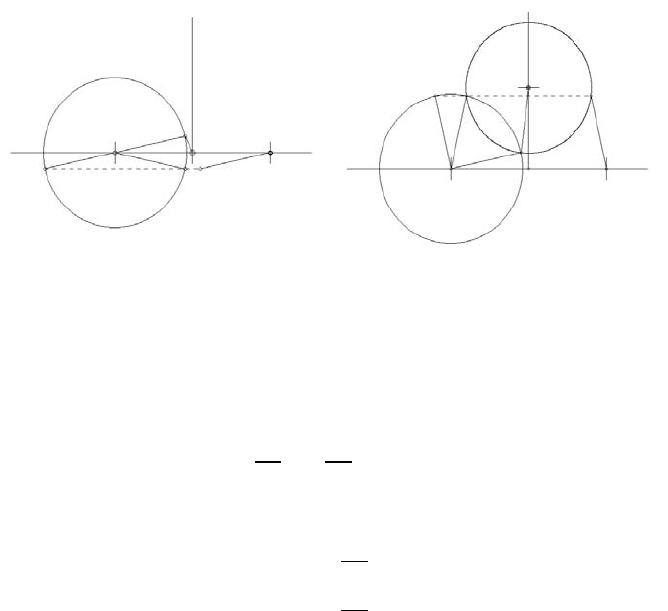
Shape and Form 201

values are (x, y) = (0.9, 0.2). Figure 9.23(a) illustrates the same case, but now the

rotation angle is θ = π. In this case the point (x, y) = (a/2, 0) indicated by two

concentric small circles is the equilibrium point. An equilibrium point located at

(x, y) = (a/2, a/2) is presented in Figure 9.23(b) where the value of the rotation

angle is θ = π/2.

(a) θ = π (b) θ = π/2

FIGURE 9.23: Geometric analogues of rotation-translation

The Jacobian determinant for the rotation-translation case above is

J = 1 + x

∂θ

∂y

− y

∂θ

∂x

= 1 + x

− y

where

∂θ

∂x

∂θ

∂y

Analogously, the Jacobian determinant for the reﬂection case is of the form

J = −1 + xθ

− yθ

Clearly, the Jacobian for the rotation-translation case is J = 1 when:

= y

This is the area-preserving case resulting when the rotation angle is expressed by any

function of the form

= f



+ y



= f





202 Chaotic Modelling and Simulation

or by functions of the radius r

+ y

Another issue is to explore relations regarding the argument z

n+2

= z

or:

n+2

, y

n+2

) = (x

, y

)

By applying the rotation-translation equation above and the last relation yields:

n+1

+ x

= a

Clearly, when x

= a/2 then from the last relation x

n+1

= a/2. Both points coincide

as the relations (x

n+1

= a/2, y

n+1

) and (x

= a/2, y

) imply that y

n+1

= y

. The more

general case z

n+m

= z

yields a relation of the form:

n+m−1

+ x

n+m−2

+ ··· + x

= m

9.8.1 The space contraction rotation-translation case

This case is expressed by the well-known function

n+1

= a + bz

iθ

where 0 < b < 1 is the space contraction parameter. The Jacobian determinant of the

space contraction rotation-translation case is:

J = b

(1 + x

− y

)

The same limit argument

n+1

, y

n+1

) = (x

, y

) = (x, y)

will give the relation

(x − a)

+ y

= b

+ y

)

or, after some algebra:



x −

1 − b



+ y

1 − b

This is the equation of a circle with radius R =

1−b

centred at (x, y) =



1−b

, 0



The resulting relations for x and y are:

x =

a(1 − b cos θ)

1 + b

− 2b cos θ

y =

ab sin θ

1 + b

− 2b cos θ

The equation for cos θ is:

cos θ =

1 + b

−

When the angle θ is a function of r, the last equation provides the values of θ for

which z

n+1

= z

Questions and Exercises

1. Show that plane isometries preserve collinearity: Let A, B, C be three distinct

collinear points. Then use the fact that the distances between T A, T B, TC must

be the same as those between A, B, C respectively to show that T A, T B, TC

must also be collinear, and in fact appear in the same order (possibly reversed).

2. Verify the properties of rotations and reﬂections given in (9.6).

3. What circles are left invariant by each of the diﬀerent isometries?

4. Change the system (9.8) by adding a translation parameter a

to the second

equation, while retaining the translation parameter a in the ﬁrst equation. Find

the axis of symmetry for this new system.

5. Change the system (9.8) by adding a translation parameter −a to the second

equation, while retaining the translation parameter a in the ﬁrst equation. Find

the axis of symmetry for this new system.

6. In the system from the previous question, use relation (9.12) to ﬁnd a chaotic

attractor of the Ikeda type. You will likely have to use several values for the

parameters.

7. Repeat the previous question, but now using reﬂection equations.

8. Find the ﬁxed points of the relation:

n+1

− b)

What is the smallest value of b for which there are three ﬁxed points? How

does the system behave when there is only one ﬁxed point?

9. Draw chaotic simulations for the circular system described by:

n+1

− b)

10. Repeat the same analysis as in the two previous questions, but now using the

relations

n+1

= b −

203