Skiadas C.H., Skiadas C. Chaotic Modelling and Simulation. Analysis of Chaotic Models, Attractors and Forms

Подождите немного. Документ загружается.

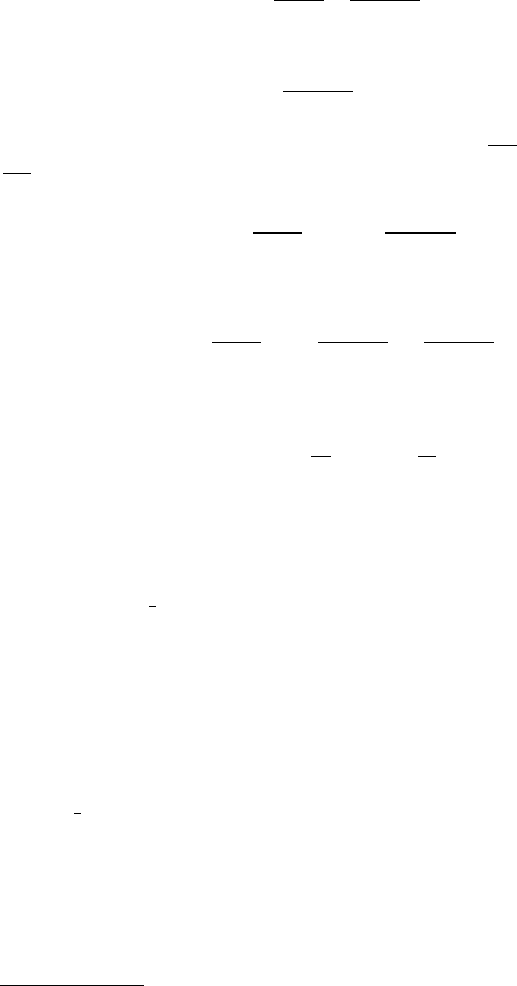
164 Chaotic Modelling and Simulation

So for a ﬁxed point we would have:

z =

1 − b

i∆θ

− b

1 − be

i∆θ

(8.16)

It can easily be veriﬁed that



i∆θ

− b

1 − be

i∆θ



= 1

and consequently all ﬁxed points lie on the circle centered at



1−b

, 0



and with radius

1−b

, in other words they satisfy:



x −

1 − b



+ y

(1 − b

)

Further, if we transform equation (8.16) back to an equation for f = f

, we get:

f =

1 − b

1 + b

i∆θ

− b

1 − be

i∆θ

1 − be

i∆θ

Therefore, the ﬁxed points f further satisfy:

cos(∆θ) =

1 + b

−

(8.17)

This equation can easily be solved provided that the angle ∆θ is a function of r.

Be begin our analysis with the case where no area contraction takes place, so that

b = 1. In this case the disk F is replaced by the entire plane. An interesting property

of the system (8.5) in this case is that the resulting map often exhibits a symmetry

along the line x =

, particularly when chaotic behaviour is present. This is diﬀerent

from the symmetry axis of the diﬀerential equation analogue where the symmetry

axis is the line x = 0. In the diﬀerence equation case, the egg-shaped form is shifted

to the right of the original positions of the system of coordinates.

As a possible explanation for this symmetry, let us consider the map in the form:

n+1

= a + f

i∆θ

For any complex number z, it can be easily seen that its reﬂection with respect to the

axis x =

is a − ¯z, where ¯z is as usual the complex conjugate of a complex number.

If we denote the reﬂection of f

by g

, then we see that:

n+1

= a −

n+1

= a −



a +

−i∆θ



= (−a + g

−i∆θ

The derivation of this is also left as an exercise to the interested reader.

Rotations 165

Multiplying through with e

i∆θ

, we see that the reﬂections satisfy a very similar recur-

sive relation, except that it goes “backwards”:

= a + g

n+1

i∆θ

Assuming that at some time the map passes very close to the x =

line, the corre-

sponding point will be very close to its reﬂection, and the evolution of the system

from that point on will be very close to the reﬂection of the history of the system up

to that point. This would cause the map to seem symmetric, especially when it ex-

hibits chaotic behaviour. Similarly, equilibrium points will tend to exhibit symmetry

around this axis.

We proceed now to discuss the equilibrium points of the system. We are therefore

searching for the points where x

n+1

= x

and y

n+1

= y

. This leads to x =

and

y =

cot



∆θ



. It is clear that there is no symmetry axis in the x direction, as y

does not show stable magnitude since it is a function of the angle ∆θ. However, an

approximation of y is achieved when the angle ∆θ is small. Then

y ≈

∆θ

The point



x =

, y =



is therefore an equilibrium point. However, it is not a

stable equilibrium point. The system may easily escape to inﬁnity when y is higher

than

(a) Rotation-translation (b) The central chaotic bulge

FIGURE 8.3: Rotation-translation, and the chaotic bulge

An important detail here is that ∆θ depends on n, so the formulas don’t quite match up, unless ∆θ

n+1

is close to ∆θ

166 Chaotic Modelling and Simulation

Figures 8.3(a) and 8.3(b) illustrate a rotation-translation case with parameters

a = 2 and MG = 100. In Figure 8.3(a), a number of paths inside the egg-shaped

formation are drawn. All the paths are analogous to those obtained by the diﬀeren-

tial equation analogue studied above, but they are moved to the right at a distance

x =

. A chaotic attractor that resembles a bulge appears around the centre of co-

ordinates. An enlargement of this attractor is illustrated in Figure 8.3(b). This is a

symmetric chaotic formation with the line x =

as an axis of symmetry.

(a) a = 0.8 (b) a = 1

FIGURE 8.4: The chaotic bulge

Figures 8.4(a) and 8.4(b) present an illustration of the chaotic bulge of the rotation-

translation model. The parameters are a = 0.8 for Figure 8.4(a) and a = 1 for

Figure 8.4(b). In both cases, MG = 100 and the rotation angle is ∆θ =

In Figure 8.4(b), third and fourth order equilibrium points appear, indicated by a

small cross and a bigger cross respectively. In this case, the following relations hold:

n+3

= x

and y

n+3

= y

, and x

n+4

= x

and y

n+4

= y

respectively.

Accordingly, in Figure 8.4(a), two equilibrium cases appear, one of second order

(indicated by small cross) where x

n+2

= x

and y

n+2

= y

and y

n+2

= y

and one of

the third order where x

n+3

= x

and y

n+3

= y

In both cases, an algorithm is introduced for the estimation of the equilibrium

points. The convergence is quite good provided that the starting values are in the

vicinity of the equilibrium points.

As the parameter a takes higher values, higher order equilibrium points appear.

A ﬁfth order equilibrium point is added to those presented before, as illustrated in

Figure 8.5(b), when a = 1.2. The relations for the new equilibrium point are x

n+5

and y

n+5

= y

. Figure 8.5(a) illustrates the case where a = 0.2. Only a ﬁrst order

equilibrium point is present.

Rotations 167

(a) a = 0.2 (b) a = 1.2

FIGURE 8.5: The chaotic bulge

Higher order bifurcation is present in Figures 8.6(a) and 8.6(b). In Figure 8.6(a),

a tenth order bifurcation form appears in the periphery of the chaotic attractor. The

magnitude of the translation parameter is a = 1.5. In Figure 8.6(b), the translation

parameter is a = 1.9. At this value, the bifurcation is so high that the chaotic region

covers all the space bounded by the egg-shaped form. The point masses following

chaotic trajectories eventually escape to inﬁnity.

(a) a = 1.5 (b) Complete chaos (a = 1.9)

FIGURE 8.6: The chaotic bulge

It is diﬃcult to ﬁnd the coordinates of equilibrium points that are located in the

centre of the islands that are in the middle of the chaotic sea of the attractor, though

168 Chaotic Modelling and Simulation

as discussed earlier those are going to be symmetric with respect to the axis x =

A ﬁrst order equilibrium point is characterised by the simple relations x

n+1

= x

and y

n+1

= y

, which lead to the following relation for the radius of the circle on the

periphery of which the equilibrium point must be located

≈

(2kπ)

, k = 1, 2, . . .

(a) a = 0.1 (b) a = 0.5

FIGURE 8.7: Equilibrium points

The circles R

introduce a set of decreasing order with regards to the magnitude

of the radius, as illustrated in Figure 8.7(a) (a = 0.1). The ﬁrst point located on

the circle with the larger radius (k = 1) is indicated by a cross. A few isoclines

indicating the limits of the island are drawn around this point. Subsequent points

follow in decreasing order. They are located in the middle of the isoclines.

The equilibrium points of higher order follow by using diﬀerent relations. A sim-

ple case is that of the estimation of the equilibrium points of the second order, that

is, when the coordinates are x

n+2

= x

and y

n+2

= y

. This assumption leads to the

following equation:

+ y

) cos

(∆θ) + 2x

cos(∆θ) + x

− y

= 0

This equation is fulﬁlled if the rotation angle obeys the relation ∆θ = (2k + 1)π.

Then, this result leads to the following relation for the radius of the circle, on the

periphery of which the equilibrium points must be located:

≈

(

(2k + 1)π

)

, k = 1, 2, . . .

Rotations 169

The simulation results are illustrated in Figure 8.7(b). The translation parameter

is a = 0.5. The concentric circles are distributed in decreasing order according to the

magnitude of the radius R

. The ﬁrst two equilibrium points are distributed in the

outer circle. They are indicated by a cross and are located on the axis of symmetry

x =

, but in opposite directions: one to the positive and one to the negative part

of the semi-plane for y. Three pairs of order two equilibrium points are illustrated

in Figure 8.8(a). The equilibrium pairs are indicated by a cross. Also, the three

equilibrium islands of the ﬁrst order are presented. The parameter is a = 0.04. As

this parameter has a very low value, the central chaotic bulge has a small radius.

(a) Equilibrium pairs (a = 0.04) (b) Order-3 bifurcation (a = 0.7)

FIGURE 8.8: The chaotic bulge

The order three equilibrium points are presented in Figure 8.8(b). They are located

in the middle of the three islands that are in the outer part of the chaotic bulge.

The translation parameter is a = 0.7. The order three equilibrium points are in the

periphery of a circle centred at (

). The radius of this circle is approximated by

R ≈

(2π/3)

−





8.4 A General Rotation-Translation Model

The solution of the diﬀerential equation of the model (8.7) leads to the form

ay + h =

(∆θ)rdr

170 Chaotic Modelling and Simulation

A simple approximation of the quantity ∆θ is:

∆θ ≈

Then, the solution has the form

ay + h =

2−

2 −

√

MG (8.18)

The special case β = 2 leads to the following equation form

ay + h = r

√

or:

+ y

)GM = (ay + h)

This equation expresses a family of ellipses (Figure 8.9(a)). The parameter a is

6, and the constant of integration h takes several values. The axis of symmetry is at

x =

. Figure 8.9(b) illustrates a chaotic central bulge. The outer part of this chaotic

attractor is approximated by an ellipse with h = MG + a

(a) A family of ellipses (b) The chaotic bulge

FIGURE 8.9: Elliptic forms and the chaotic bulge

When β = 4, the resulting equation for (x, y) is:

√

MG ln(r) = ay + h

The rotating forms are egg-shaped and similar to those provided in earlier rotation

forms. With the exception of β = 2, where the rotation paths are elliptic, the cases

with β > 2 provide egg-shaped rotation forms.

Rotations 171

Another very important property of the elliptic case (β = 2) is that the rotating par-

ticles remain in the elliptic paths even if high values for the parameter h are selected.

In the limit when the parameter a approaches zero the ellipses turn to concentric

circles.

8.5 Rotating Particles inside the Egg-Shaped Form

Two cases are of particular importance. In the ﬁrst case, the translation parameter

a is quite small, and the particles are trapped inside the egg-shaped form and remain

there, following the trajectories proposed by the theory discussed so far. However, a

smaller region inside the trapping region exhibits chaotic behaviour. In this region,

the particles follow chaotic paths that form the attractors presented above. In Fig-

ure 8.10(a), the outer limits of the egg-shaped form are drawn, and a disk of rotating

particles of equal mass is centered at (0, 0). The particles are distributed by follow-

ing the inverse law for the density ρ given by ρ =

. The diameter of the disk is

chosen as to be exactly within the limits of the egg-shaped form. The parameters are

a = 0.25 and GM

= 0.45. The rotation angle is given by

∆θ =

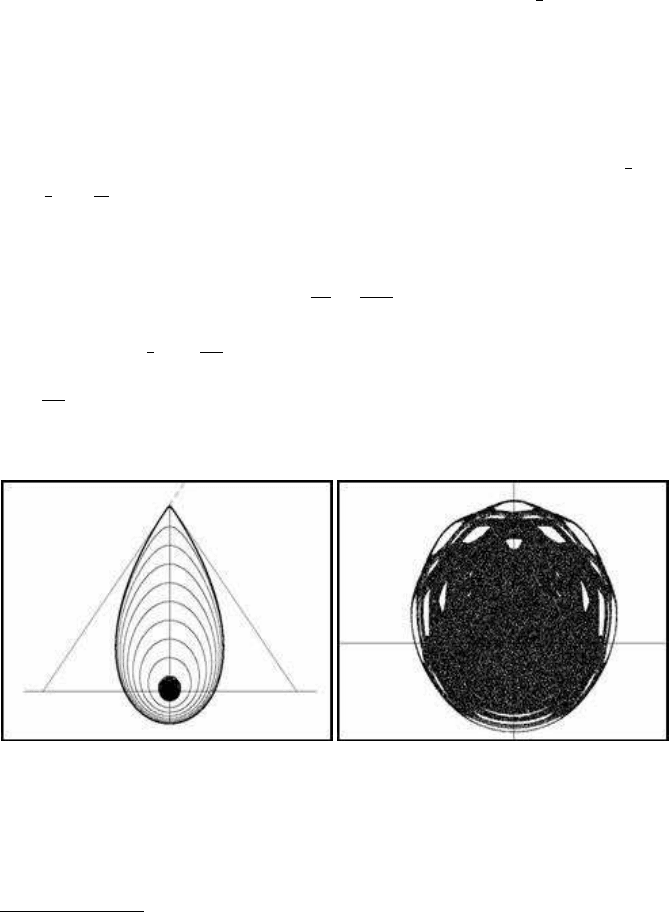
The resulting form that the disk of rotating particles takes after time t = 10 appears

in Figure 8.10(b). The original cyclic form has now changed, providing an outer form

of rotation and an inner chaotic attractor-like object.

Figures 8.10(c) and 8.10(d) illustrate the resulting picture after time t = 20 and

t = 100 respectively. The distinct inner attractor is more clearly formed. In the case

presented in Figure 8.10(d), the outer part of the rotating object extends to almost the

entire space of the shape, but by following very speciﬁc characteristic paths.

In the second case, the translation parameter is high enough so that all of the

egg-shaped space is contained in the chaotic region. The system is unstable and

the rotating particles are not retained inside the egg-shaped region. On the con-

trary, they escape by following the escape trajectories and move away from the egg-

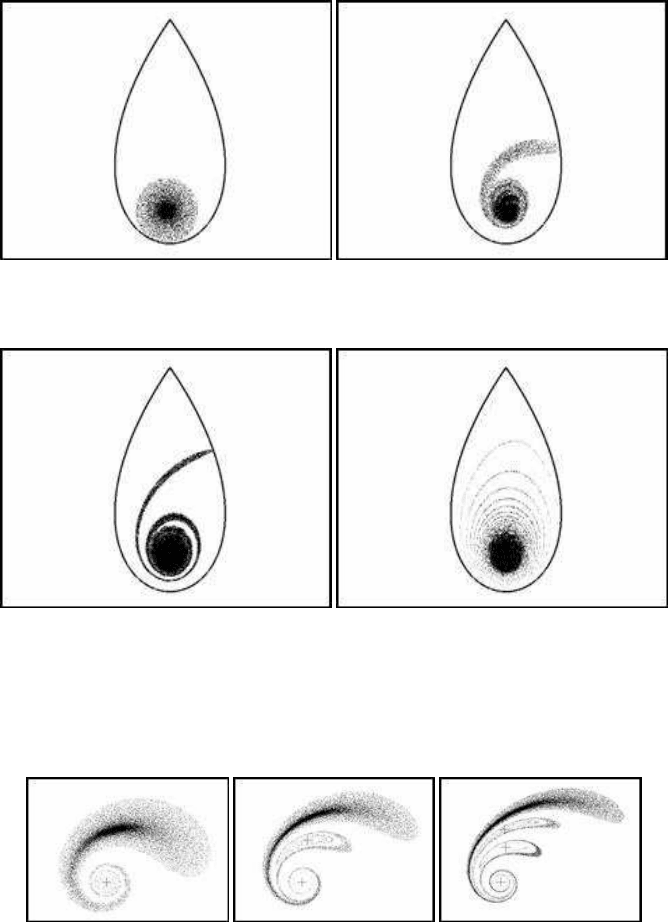
shaped region. After a while, the majority of the particles will leave the region. Fig-

ures 8.11(a), 8.11(b) and 8.11(c) illustrate three instances, in times t = 2, t = 3 and

t = 4 respectively. The translation parameter is a = 0.6. The cross in Figure 8.11(a)

is at (x, y) = (a, 0). A cross indicates the characteristic centres of the chaotic forms.

These coordinates are calculated by using as starting values in a repeated procedure

x = a and y = 0. The iterative procedure is based on the diﬀerence equations for x

and y.

The case when t = 10 appears in Figure 8.12. The rotating system of particles

is in an intermediate stage. It escapes from the egg-shaped form, but a part of the

system remains around the location (x, y) = (a, 0) inside the egg-shaped form. When

172 Chaotic Modelling and Simulation

(a) t = 0 (b) t = 10

FIGURE 8.10: Rotating particles

(a) t = 2 (b) t = 3 (c) t = 4

FIGURE 8.11: Development of rotating particles over time (a = 0.6).

Rotations 173

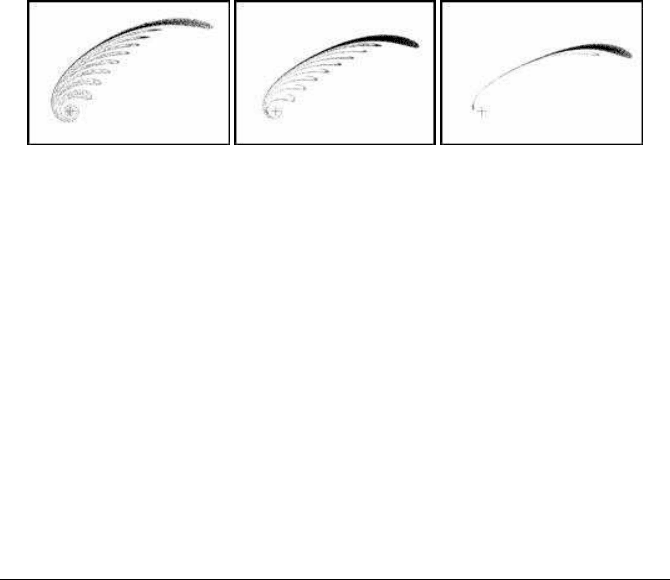
the magnitude of the translation parameter takes higher values, all the particles es-

cape after a short interval (Figure 8.12(a)). An intermediate stage appears in the

Figure 8.12(b), with parameter a = 0.7 and time t = 10. The leaf-like structure starts

to disappear inside the egg-shaped form when close to (x, y) = (a, 0). These jets eject

material through the trajectories of the model. The speed of these jets depends on the

magnitude of the parameter a and on the original rotation speed. The speed and the

direction of the jets of material coincides to a after a large enough amount of time t.

Figure 8.12(c) illustrates the case when a = 0.8. Only the last part of the jet remains

connected to the source of the chaotic sea inside the egg-shaped pattern.

(a) a = 0.6 (b) a = 0.7 (c) a = 0.8

FIGURE 8.12: Development of rotating particles according to the magnitude

of the translation parameter. The elapsed time is t = 10.

When the translation parameter is a = 1 (t = 10), all the rotating material escapes

outside the egg-shaped pattern. In Figure 8.13(a), the original cyclic disk is quite

large, and a part of this disk lies outside the egg-shaped formation. However, all

the material follows the escape route as a compact formation. On the other hand,

in Figure 8.13(b), the inﬂuence of a small translation parameter (a = 0.25) to an

original large cyclic cloud has a critical impact to the cloud formation. After t = 100,

the cloud is separated into two formations, the ﬁrst inside the egg-shaped form with

the chaotic bulge-form in the middle, and the second outside.

8.6 Rotations Following an Inverse Square Law

We return to the original system of diﬀerential equations

˙x = a − y∆θ

˙y = x∆θ

(8.19)