Skiadas C.H., Skiadas C. Chaotic Modelling and Simulation. Analysis of Chaotic Models, Attractors and Forms

Подождите немного. Документ загружается.

154 Chaotic Modelling and Simulation

Questions and Exercises

1. Consider the system

˙x = −y

˙y = x(1 − x)

(a) Find its equilibrium points.

(b) Find the eigenvalues and eigenvectors at the equilibrium points, and char-

acterise the points according to their stability.

points.

(d) Find a ﬁrst integral of motion for the system.

(e) Draw various trajectories of the system in the (x, y) plane.

(f) Draw the trajectories that pass through equilibrium points.

(g) Find the maximum speed of the ﬂow at the y direction (˙y).

2. Consider the system

˙x = 1 − y

˙y = x + ay

(a) Find the equilibrium points for the system.

(b) Find the characteristic equation at the equilibrium points.

(d) Examine in particular the case a = 2.

3. For each of the following systems, (a) show that it is Hamiltonian, (b) com-

pute the Hamiltonian function, (c) determine the ﬁxed points, and classify

them, and (d) plot, for various values of the parameters, the level curves of the

Hamiltonian, including the curves passing through the ﬁxed points.

(a)

˙x = y(y − b)

˙y = ax

(b)

˙x = y

− b

˙y = x

(c)

˙x = y

− b

˙y = x

− a

4. Show that the system

˙x = 2xy

˙y = x

− y

is conservative, but not Hamiltonian. Find a system equivalent to it that is

Hamiltonian.

Non-Chaotic Systems 155

5. Show that the system

˙x =

˙y = −

is conservative, but not Hamiltonian. Find a system equivalent to it that is

Hamiltonian.

6. Show that each of the transformations described in section 7.2.1 have the indi-

cated eﬀect on the matrix A and its eigenvalues.

Chapter 8

Rotations

In this chapter we examine the eﬀects of introducing aﬃne transformations to mod-

els, in particular the eﬀect of introducing rotation. A wealth of very interesting

models arise from this seemingly simple change.

8.1 Introduction

The location (x

, y

) of a system is given in parametric form (r

, θ

) by:

= r

cos(θ

)

= r

sin(θ

)

(8.1)

where r =

+ y

and θ

is the rotation angle.

If we assume that transitioning from the n-th state to the n + 1-st state amounts to

a rotation by an angle ∆θ, then the new coordinates would be given by:

n+1

= r

cos(θ

+ ∆θ)

n+1

= r

sin(θ

+ ∆θ)

(8.2)

or after using the familiar trigonometric identities for the sum of two angles:

n+1

= r



cos(θ

) sin(∆θ) − sin(θ

) sin(∆θ)



n+1

= r



cos(θ

) sin(∆θ) + sin(θ

) cos(∆θ)



(8.3)

Therefore, the eﬀect of rotation can be written directly using the following, which

may be familiar to you already:

n+1

= x

cos(∆θ) − y

sin(∆θ)

n+1

= x

sin(∆θ) + y

cos(∆θ)

(8.4)

When the rotation is followed by a translation equal to a and parallel to the x axis,

then the tranformation (8.4) is replaced by:

n+1

= a + x

cos(∆θ) − y

sin(∆θ)

n+1

= x

sin(∆θ) + y

cos(∆θ)

(8.5)

157

158 Chaotic Modelling and Simulation

We can consider the system (8.5) as a simple system of diﬀerence equations. Let us

work out an analogous system of diﬀerential equations. The time elapsed between

two successive iterations is ∆t and is usually set to 1. Then, taking into account that

˙x =

≈

∆x

∆t

= x

− x

n−1

and similarly for ˙y, we obtain the diﬀerential equations:

˙x = a + x



cos(∆θ) − 1



− y sin(∆θ)

˙y = x sin(∆θ) + y



cos(∆θ) − 1



(8.6)

8.2 A Simple R otation-Translation System of Diﬀeren-

tial Equations

If the rotation angle is small, ∆θ ≪ 1, the system (8.6), using ﬁrst order Taylor

approximations for cos and sin, can be simpliﬁed to:

˙x = a − y∆θ

˙y = x∆θ

(8.7)

This is a Hamiltonian system, whose ﬁrst integral of motion can be computed from

the diﬀerential equation:

∂y

∂x

x∆θ

a − y∆θ

This equation leads to the form:

ady = (∆θ)rdr (8.8)

The solution of equation (8.8) depends on the form of the function ∆θ. A reason-

able assumption would be that ∆θ is “radial,” i.e. depends only on the distance r from

the origin, and not of the direction. A standard choice in mechanics, based on the

transverse component of the acceleration, is that the rotational change is inversely

proportional to the square distance, i.e. that:

∆θ ≈

Another important case is that of a mass M rotating in a circular orbit under a

central force

f (r) =

We have used here that r

= x

+ y

, and consequently rdr = xdx + ydy.

Rotations 159

where G is the gravity constant. The equations of motion then result in

∆θ ≈

θ =

In this case, equation (8.8) becomes:

ady =

Its solution is

r =

(ay + h)

4MG

where h is an integration constant. This can also be rewritten as

(ay + h)

4MG

− y

(ay + h)

4MG

+ y

(8.9)

The ﬁxed point of the system is at

(x, y) =





at which point the value of h is:

h =

The path of the trajectory in the (x, y) plane for this value of h divides the plane in

two segments. When h >

, the trajectories diverge and the rotating object heads

oﬀ to inﬁnity. When h <

the rotating mass moves inside the space bounded by

the above trajectory.

FIGURE 8.1: The limiting trajectory

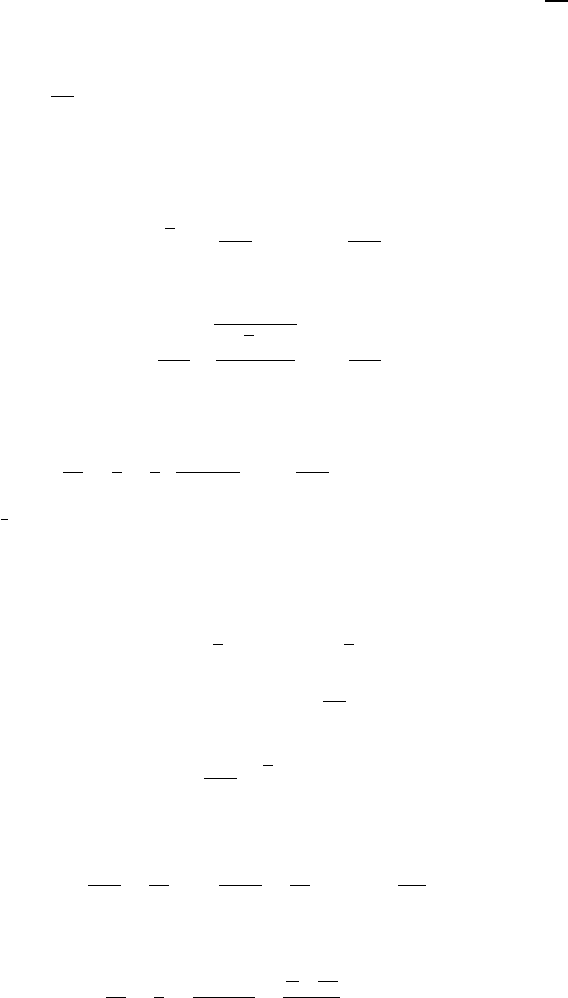
160 Chaotic Modelling and Simulation

Some very interesting properties of equation (8.8) are illustrated in Figure 8.1.

The trajectory in the limit of escape has an egg shape, similar to but diﬀerent from

those discussed in Chapter 7. The sharp corner is at the maximum value of y =

where x = 0. This is the ﬁxed point for the system, which is not stable.

The minimum value of y is that where the maximum rotation speed is achieved.

This can be found by setting x = 0 in equation (8.9). This gives us two solutions, the

ﬁxed point at y =

as already discussed, and the solution to the equation:

(ay + h)

= −4ahy

The largest solution of this equation is:

y =



√

2 − 3



≈ −0.1716

(8.10)

The maximum value of x is given by:

max

√

5 − 11

≈ 0.3

This is computed by equating to zero the ﬁrst derivative of x with respect to y, that

is:

∂x

∂y

˙x

˙y

8(MG)



ay +



− y

= 0 (8.11)

Setting z =

y, equation (8.11) becomes:

(z + 1)

= 8z

This can be easily seen to have the three roots:

z = 1, z =

√

5 − 2, z = −

√

5 − 2

The ﬁrst of these corresponds to the ﬁxed point





. The second is the one we

are after, and the corresponding y value is:

y =

(

√

5 − 2)

When y = 0, then

x =

, r =

4MG

and ∆θ =

so from (8.7) we get:

˙y

˙x

x∆θ

a − y∆θ

= 2

Rotations 161

This tangent appears in Figure 8.1.

The tangent at the top sharp corner of the egg-shaped path can be seen by writing

equation (8.8) in a coordinate system centered at this point. For this reason, let:

z = y −

= y −

Then, in terms of (x, z), equation (8.8) can be written as:

0 = −x

+ 2z +

= −x

+ ···

where the omitted terms are of higher order in z. This means that near (x, z) = (0, 0),

our orbit behaves exactly like the function:

0 = −x

√

z − x

√

z + x

So the two tangent lines are given by the equations:

y =

√

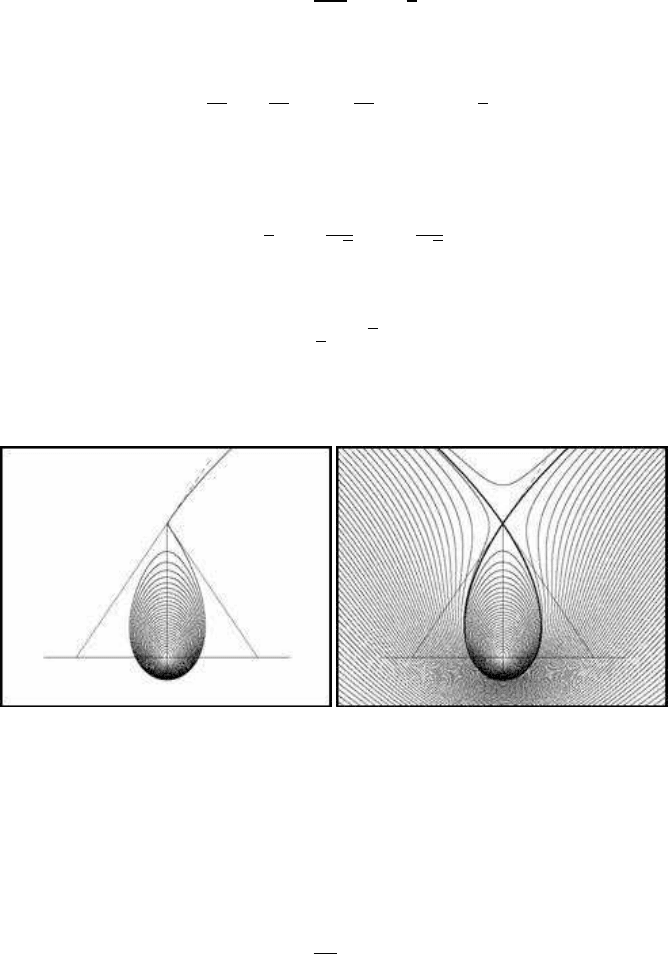
(a) Rotating paths (b) Paths in the plane

FIGURE 8.2: Rotating paths

Figure 8.2(a) illustrates the path of a moving particle. The particle follows an anti-

clockwise direction. It starts from a point near zero and rotates away from the centre

until the highest permitted place. Then, it escapes to inﬁnity following the tangent on

the top of the egg-shaped path. In Figure 8.2(b), a large number of paths are drawn.

Every path has the same value for h =

. The paths outside the egg-shaped limits

162 Chaotic Modelling and Simulation

have direction from left to right and they do not transverse the egg-shaped region of

the plane. The iterative formula used for the above simulations is:

n+1

= x



a − y

√

MGr



n+1

= y

+ x

√

MGr

+ y

(8.12)

where, for the above ﬁgures, a = 2, MG = 100 and d = 0.05.

Other interesting properties of the aforementioned egg-shaped forms arise by us-

ing elements from mechanics. From the equations of motion, it is clear that the para-

meter a is a constant speed with direction parallel to the x axis. The rotational speed

has two components: ˙x, ˙y. However, at the top and at the bottom of the egg-shaped

form only the x component of the velocity is present, since x = 0. The rotational

speed, or the transverse component of the velocity, is v =

. This speed must be

equal to a. Thus, without using the equations for the trajectories, the value of y at

the top, x = 0, is estimated from the equality v − a = 0. Thus,

= a

and

y =

To obtain the equation for the total speed at the lower point of the curve, we must

take into account that this speed must be equal to the escape speed:

v + a = v

esc

(8.13)

The escape speed for a mass rotating around a large body is known from mechanics

to be:

esc

2MG

Thus, equation (8.13) becomes:

+ a =

2MG

Finally, from this last equation the value of y is:

y =

(

√

2 − 1)

This is, up to a sign, the same result obtained in equation (8.10). It is obvious

that the system in these particular cases obeys the laws of classical mechanics. This

egg-like form is a set of vortex curves with relative stability and strength.

Rotations 163

8.3 A Discrete Rotation-Translation Model

The analysis above is signiﬁcant in helping us understand the dynamics under-

lying the rotation analogue in the discrete case. The iterative scheme based on the

diﬀerence equations for rotation-translation is more diﬃcult to handle analytically,

but, on the other hand, it is closer to a real life situation. No approximation is needed,

whereas, the egg-shaped scheme and the trajectories are retained. Moreover, the tra-

jectories inside the egg-shaped boundary are perfectly closed loops. Additionally, the

chaotic nature of the rotation-translation procedure near the centre becomes appar-

ent. In the equations (8.4), we introduce an area contracting parameter b (0 < b < 1),

and the ﬁnal equations used are the following

n+1

= a + b

(

cos ∆θ − y

sin ∆θ

)

n+1

= b

(

sin ∆θ + y

cos ∆θ

)

(8.14)

where the same approximation

∆θ

≈

is used.

A convenient formulation of the last iterative map expressing rotation and transla-

tion is achieved by using the following diﬀerence equation

n+1

= a + b f

i∆θ

(8.15)

where f

= x

+ iy

The Jacobian determinant of this map is J = b

= λ

. This is an area contracting

map if the Jacobian J is less than 1. The eigenvalues of the Jacobian are λ

and λ

and the translation parameter is a.

A very interesting property of the map (8.14) is the existence of a disk F of radius

1−b

centered at (a, 0) in the (x, y) plane. The points inside the disk remain inside it

under the map.

To locate the ﬁxed points of this transformation, let us change coordinates by

setting:

= f

−

1 − b

Then the transformation can be rewritten as:

n+1

− z



i∆θ

− 1



+ ab

i∆θ

− b

1 − b

This fact is left as an exercise for the reader.