Skiadas C.H., Skiadas C. Chaotic Modelling and Simulation. Analysis of Chaotic Models, Attractors and Forms

Подождите немного. Документ загружается.

144 Chaotic Modelling and Simulation

This case is illustrated in Figures 7.2(e) and 7.2(f).

To summarise, the behaviour of solutions near an equilibrium point falls under one

of the following cases:

1. ∆ = 0. This is the degenerate case.

2. ∆ > 0. Then λ

1,2

are both real. The behaviour in this case depends a lot on their

sign. If they are both negative, then all solutions tend toward the equilibrium

point, which in this case is called a stable point, or also a stable node. If they

are both positive, then the solutions tend away from the equilibrium point, and

the point is classiﬁed as unstable.

Otherwise, λ

1,2

are both real, but with opposite signs. In this case, there is a

stable direction and an unstable direction, indicated by the negative and pos-

itive eigenvalues respectively. The equilibrium point is then called a saddle

point.

3. ∆ < 0. Then λ

1,2

have non-zero real and imaginary parts. If the real part is

negative, then the solutions spiral toward the equilibrium point, which is called

in this case a stable spiral or a spiral sink. If, on the other hand, the real part

is positive, then the solutions spiral away from the critical point, and the point

is then called an unstable point or a spiral source.

A special case is when λ

1,2

have only an imaginary part (i.e. when the real part

is zero). The critical point is then called a center.

7.3 Egg-Shaped Forms

7.3.1 A simple egg-shaped form

We now proceed to examine certain Hamiltonian systems that give rise to very

interesting egg-shaped forms. The ﬁrst such system is:

˙x = y(y − b)

˙y = x

(7.18)

This is a Hamiltonian system, since

∂

∂x



y(y − b)



= 0 = −

∂

∂y

(

)

The Hamiltonian is easily seen to be

H(x, y) = −

− b

+ h

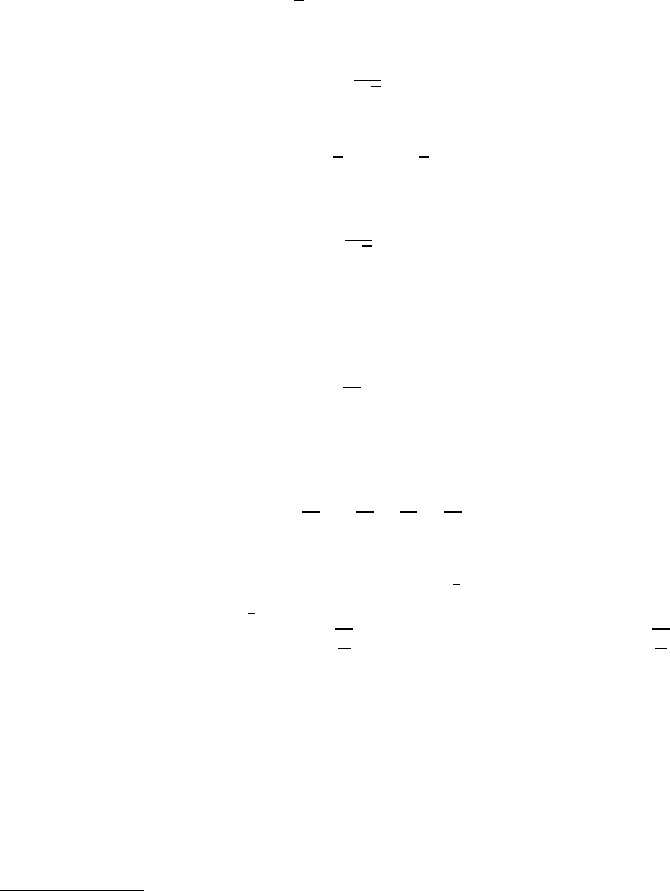
Non-Chaotic Systems 145

This system has two equilibrium points, at

(x, y) = (0, 0) and (x, y) = (0, b)

The ﬁrst of these is a stable point, as the quadratic form,

−



+ by



has two imaginary roots:

1,2

= ±

√

The second point, however, is unstable, since its characteristic polynomial,

−2 + 2bX

= 2(

√

bX − 1)(

√

bX + 1)

has two real roots:

λ = ±

√

These are exactly the slopes of the two tangent lines at (0, b).

For convenience, we will choose the integration constant in H to be such, that H

is 0 at this, second, equilibrium point, namely:

h =

The level curve that passes through (0, b) is shown, marked with a heavy line, in

Figure 7.3(a) (b = 0.6). It has equation:

H(x, y) = −

− b

The sharp (top) corner of the egg-shaped form is located at the equilibrium point

(0, b), whereas the bottom of the form is at the point



0, −



At this point, the speed

of the particle is given by ˙x =

. The boundaries of the egg-shaped form in the x

direction are when y = 0, namely x = ±

. The speed at these points is ˙y = ±

respectively.

7.3.2 A double egg-shaped form

A double egg-shaped form with interconnected sharp corners is expressed by the

following system:

˙x = −y(y − a)(y − b)

˙y = x

(7.19)

This is found by solving the cubic polynomial H(0, y) = 0 This will have a double root at y = b, and

one more root.

146 Chaotic Modelling and Simulation

−0.3 −0.2 −0.1 0.0 0.1 0.2 0.3

−0.4

−0.2

0.0

0.2

0.4

0.6

0.8

(a) An egg-shaped form

−0.3 −0.2 −0.1 0.0 0.1 0.2 0.3

0.0

0.5

1.0

(b) A ﬁgure eight form

FIGURE 7.3: Egg-shaped forms

where we will assume that 0 < b < a. The Hamiltonian in this case is

H(x, y) = −

+ (a + b)

− ab

−

(b − 2a)

Figure 7.3(b) shows the trajectories when a = 1 and b = 0.6.

The ﬁrst egg-shaped form at the top of the ﬁgure has a stable equilibrium point

at (a, 0), whereas the other egg-shaped form has a stable equilibrium point located

at (0, 0). An unstable point is located at (0, b), where the sharp corners of the two

egg-shaped forms coincide.

When the initial values are x

= 0 and y

= −b, a ﬁgure eight shape appears. This

is a characteristic level curve marked by a heavy line in Figure 7.3(b). The integration

constant has the value h = −

for this particular case. Inside this form the

trajectories follow closed loops, and the same holds outside this characteristic level.

7.3.3 A double egg-shaped form with an envelope

A double egg-shaped form enclosed in an external envelope is provided by the

following system:

˙x = y(y

− b

)(y + a)

˙y = x

(7.20)

The constant was again chosen, so that the Hamiltonian is zero at the unstable point.

Non-Chaotic Systems 147

The Hamiltonian of this system is given by:

H(x, y) =

+ a

− b

− ab

−

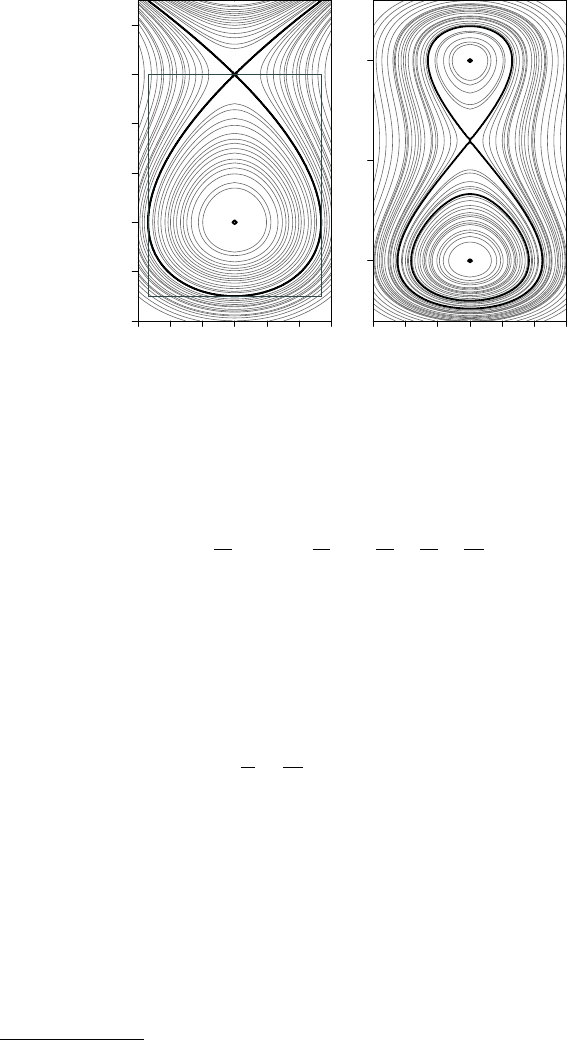
where we’ve set the integration constant to zero for simplicity. Figure 7.4 illustrates

this case where a = 1 and b = 0.6. The ﬁrst egg-shaped form at the top of the ﬁgure

has a stable equilibrium point at (0, 0), whereas the second egg-shaped form has a

stable equilibrium point at (0, −a). There are two unstable points, one at (0, −b),

where the sharp corners of the two egg-shaped forms coincide, and one at (0, b),

where the envelope is formed. The level curves through those two unstable points

are marked with a heavy line in the graph. For this particular case, corresponding

values of the Hamiltonian on these curves are

b−

= −

−

(7.21)

Inside the envelope, the trajectories follow closed loops, whereas, outside of it, the

trajectories diverge to inﬁnity.

−0.4 −0.2 0.0 0.2 0.4

−1.0

−0.5

0.0

0.5

1.0

FIGURE 7.4: A double egg-shaped form with an envelope

148 Chaotic Modelling and Simulation

7.4 Symmetric Forms

We consider now certain forms that exhibit symmetry. A simple symmetric Hamil-

tonian form is based on the system:

˙x = y(y − b)

˙y = x(x − b)

(7.22)

The corresponding Hamiltonian is

H(x, y) =

− x

− b

− x

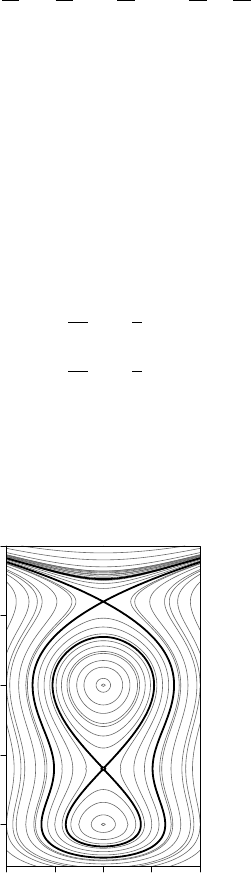
The level curves at level 0 are marked by a thick line in Figure 7.5(a). There are two

stable points, at (b, 0) and (0, b), and two unstable points, at (0, 0) and (b, b).

A slight change to (7.22) gives rise to another double-shaped form, with symmetry

with respect to the y = x axis. The equations are:

˙x = −y(y − b)

˙y = x(x − b)

(7.23)

The Hamiltonian is

H(x, y) =

+ x

− b

+ x

The level curve for the outer periphery has level −

, and is illustrated in Fig-

ure 7.5(b). The stable equilibrium points are located at (0, 0) and (b, b), whereas

the two unstable points are located at (0, b) and (b, 0). The three points of the level

curve located on the line x = y are: the point





, and the other two solutions of

the equation 4x

− 6bx

+ b

= 0.

A simple non-symmetric form is expressed by the following two equations:

˙x = −y(y − b)

˙y = x(x − a)

(7.24)

The Hamiltonian in this case is

H(x, y) =

+ x

−

+ ax

There are two characteristic level curves, passing through the unstable points (a, 0)

and (0, b) respectively, and with corresponding levels h

= −

and h

= −

respectively. These level curves are shown in Figure 7.6, marked with a thick line.

There are two stable equilibrium points, at (0, 0) and (a, b).

An interesting three-fold shape is given by the system

˙x = y(y

− b

)

˙y = x(x − b)

(7.25)

Non-Chaotic Systems 149

−0.4 −0.2 0.0 0.2 0.4 0.6 0.8

−0.4

−0.2

0.0

0.2

0.4

0.6

0.8

(a)

−0.4 −0.2 0.0 0.2 0.4 0.6 0.8

−0.4

−0.2

0.0

0.2

0.4

0.6

0.8

(b)

FIGURE 7.5: Symmetric forms

−0.5 0.0 0.5 1.0

−0.5

0.0

0.5

1.0

FIGURE 7.6: A simple non-symmetric form

150 Chaotic Modelling and Simulation

The corresponding level curves of the Hamiltonian

− b

−

+ b

are shown in Figure 7.7(a) (b = 0.85).

−0.5 0.0 0.5 1.0 1.5

−1.0

−0.5

0.0

0.5

1.0

(a) b = 0.85 >

−0.5 0.0 0.5 1.0

−1.0

−0.5

0.0

0.5

1.0

(b) b = 0.6

−0.2 0.0 0.2 0.4 0.6

−0.6

−0.4

−0.2

0.0

0.2

0.4

0.6

FIGURE 7.7: A symmetric three-fold form

There are two characteristic levels for H, which provide the level curves marked

by a heavy line. The ﬁrst value, h = 0, corresponds to the equilibrium point (0, 0),

and gives the central formation. This curve also passes through the point (

b, 0)

where x takes its maximum value in the bounded part of this curve.

The second characteristic level is h =

−

, for which the level curve passes

through the two unstable equilibrium points (b, ±b). There are three stable equilib-

rium points, two at (0, ±b), where H = −

, and one at (b, 0), where H =

The shape varies a lot depending on the parameter b. When b >

, we get a ﬁgure

similar to Figure 7.7(a). When b =

, the two characteristic curves coincide, and the

corresponding graph is shown in Figure 7.7(b). When b <

, the two curves are not

so interrelated (Figure 7.7(c)).

7.5 More Complex Forms

More complex forms appear by adding new terms in the right-hand side of the

Hamiltonian equations of the two-dimensional system. The four-type symmetric

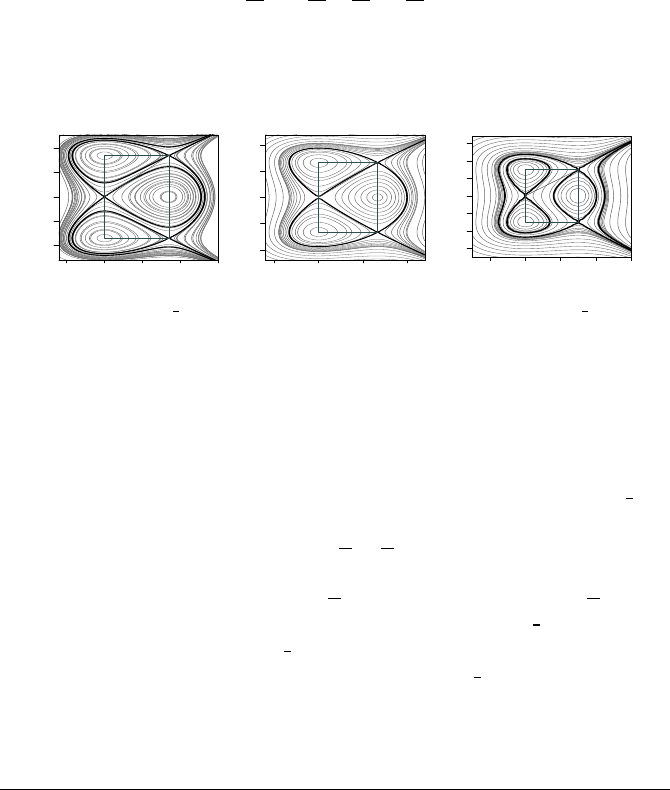
form illustrated in Figure 7.8(a) corresponds to the system

˙x = −y(y

− b

)

˙y = x(x

− b

)

(7.26)

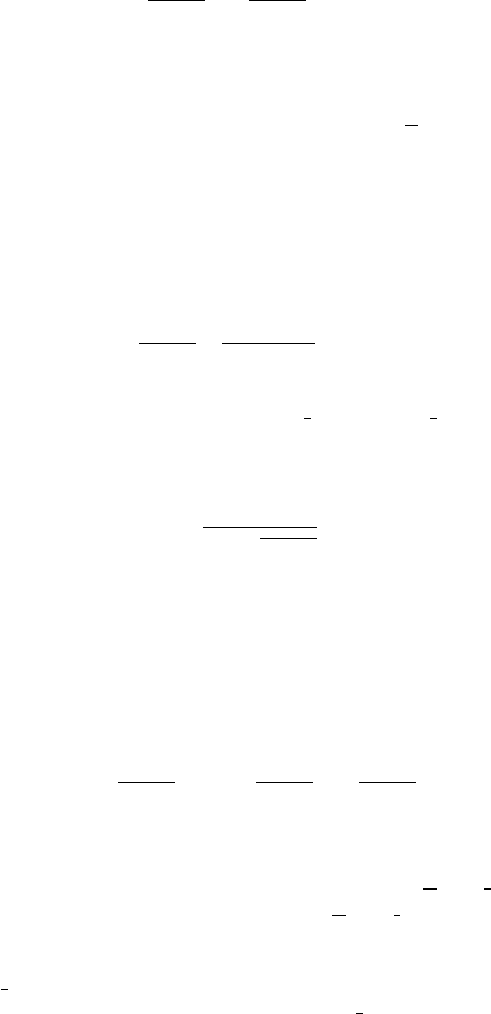
Non-Chaotic Systems 151

with Hamiltonian:

+ y

− b

+ y

There are ﬁve stable equilibrium points, one at the origin (0, 0), and the other four

located at the symmetric points (b, b), (b, −b), (−b, b) and (−b, −b). There are also

four unstable equilibrium points located at (0, b), (0, −b), (b, 0) and (−b, 0). The

level curve passing through those equilibrium points has level −

. In Figure 7.8(a),

a heavy line marks this critical level curve.

Introducing a new parameter a into (7.26), the following system arises:

˙x = −y(y

− b

)

˙y = x(x

− a

)

(7.27)

Its Hamiltonian is

+ y

−

+ b

This system has a richer structure, as illustrated in Figure 7.8(b) (a = 0.7, b = 0.5).

Two distinct level curves appear, for values H = −

and H = −

respectively.

The ﬁrst curve is associated with two 8-shape forms of Figure 7.8(b). The second

curve is associated with the other more complicated form, also marked with a heavy

line. The four points located on the x axis (y = 0) are given by:

x = ±

√

− b

If the parameter a is introduced in both equations, then an interesting system

arises:

˙x = −y(y − a)(y − b)

˙y = x(x − a)(x − b)

(7.28)

Its Hamiltonian is:

H(x, y) =

+ y

− (a + b)

+ y

+ ab

+ y

The model, with parameters equal to a = 0.8 and b = 0.3, is illustrated in Fig-

ure 7.8(c).

There is an outer characteristic level curve, with level h

= −

, and

an inner characteristic level curve, with level h

= −

b. There are ﬁve

stable points located at (0, 0), (a, a), (b, b), (a, 0) and (0, a), and four unstable points

at (b, 0), (0, b), (a, b) and (b, a).

When b =

a, then h

= 0, and the system leads to a perfect symmetry, illustrated

in Figure 7.8(d) when the parameters are a = 0.8 and b =

= 0.4.

152 Chaotic Modelling and Simulation

−1.0 −0.5 0.0 0.5

−1.0

−0.5

0.0

0.5

(a) A 4-type symmetric form

−1.0 −0.5 0.0 0.5 1.0

−0.5

0.0

0.5

(b) Two 8-shape forms with an envelope

−0.2 0.0 0.2 0.4 0.6 0.8 1.0

−0.2

0.0

0.2

0.4

0.6

0.8

1.0

−0.2 0.0 0.2 0.4 0.6 0.8 1.0

−0.2

0.0

0.2

0.4

0.6

0.8

1.0

(d) A perfect symmetry

FIGURE 7.8: More complex forms

Non-Chaotic Systems 153

7.6 Higher-Order Forms

We conclude this section with a couple of much more complicated examples, aris-

ing from systems whose equations involve higher-order polynomials. One such ex-

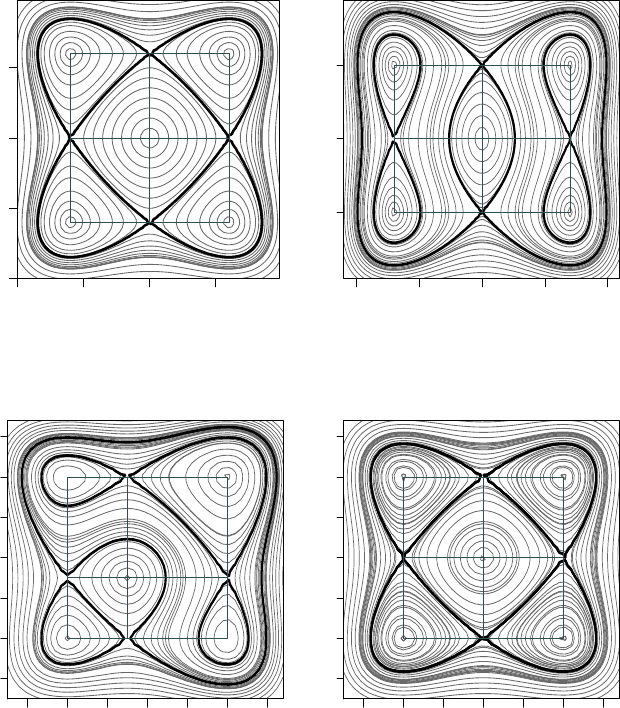
ample, illustrated in Figure 7.9(a), is the system:

˙x = −(y − a)(y − b)(y − c)(y − e)(y − f )

˙y = (x − a)(x − b)(x − c)(x − e)(x − f )

(7.29)

The Hamiltonian can be easily computed from the above equations, but we will omit

the tedious task here.

The parameters were set to a = 0.1, b = 0.6, c = 0.9, e = 1.5 and f = 2. There

are 13 stable equilibrium points, and 12 unstable equilibrium points. Equilibrium

regions and regions with high movement (ﬂows) appear. As in the simpler cases,

(a) Symmetry only along y = x axis (b) Multiple symmetries

FIGURE 7.9: Higher-order forms

appropriate values for the parameters lead to symmetric forms, as in Figure 7.9(b),

where the parameters are a = 0, b = 0.5, c = 1, e = 1.5 and f = 2.