Skiadas C.H., Skiadas C. Chaotic Modelling and Simulation. Analysis of Chaotic Models, Attractors and Forms

Подождите немного. Документ загружается.

114 Chaotic Modelling and Simulation

(a) a = 1.2 (b) Close look at the two shapes, a = 0.8

FIGURE 5.19: The sine delay model for b = 1

FIGURE 5.20: The sine delay model (a = 0.1)

The H´enon Model 115

Questions and Exercises

1. Verify that the ﬁxed points and period-doubling bifurcations of the H

enon map

for b = 1 and b = −1 are as described in section 5.1.

2. Examine the behaviour of the H

enon map for b = 3.

3. For each of the maps (5.9), (5.10) and (5.11):

(a) Determine the ﬁxed points and second-order ﬁxed orbits, and their sta-

bility.

(b) Rewrite them as systems of 3 diﬀerence equations without delay, and

calculate the Jacobian determinants of these systems.

4. Determine the ﬁxed points of the sine delay model given by equation (5.18)

when b = 1, and their stability. Use this information to explain the carpet-like

forms arising when b = 1 (Figure 5.19(a)).

5. Continuing from the previous question, run simulations with diﬀerent para-

meter values, and examine whether the carpet-like formations are present, and

how they spread across the plane.

6. Explain why for small b there is a relationship between the maxima and min-

ima of the sine delay model (x

, x

t+1

) map and the maxima and minima of the

equation for the ﬁxed points of the map.

7. Estimate the number of maxima and minima of the ﬁxed point equation for the

sine delay model:

f (x) = (1 − b)x − a sin(x)

Hint: Find an equation for those maxima and minima from f

′

(x) = 0, and

estimate the n beyond which f (c) > 0 at the minima.

Chapter 6

Three-Dimensional and

Higher-Dimensional Models

In this chapter, we present a number of higher-dimensional models that exhibit

chaotic behaviour. Before we delve into particular examples, though, a general dis-

cussion of the behaviour of such systems near their equilibrium points is necessary.

6.1 Equilibrium Points and Characteristic Matrices

Let us consider a general autonomous system of the form

˙x = ˙x(x, y, z)

˙y = ˙y(x, y, z)

˙x = ˙z(x, y, z)

(6.1)

and suppose x

= (x

, y

, z

) is an equilibrium point for it, i.e. a point where

= ( ˙x

, ˙y

, ˙z

) = (0, 0, 0).

Consider the matrix:

A =







∂ ˙x

∂x

∂ ˙x

∂y

∂ ˙x

∂z

∂˙y

∂x

∂˙y

∂y

∂˙y

∂z

∂˙z

∂x

∂˙z

∂y

∂˙z

∂z







Then, at a point x = x

+ h suﬃciently close to x

, we can assume, using a ﬁrst order

Taylor approximation, that

x is given by:

x =

+ A · h = A · h

Suppose now that the matrix A has a real eigenvalue, say λ

, with eigenvector

. Then, the orbit of a particle placed at x

+ δh

will move away from x

, in the

direction of the vector h

, since its position after a short time t would be:

x(t) ≈

(

+ δh

)

x · t = x

+ (δ + λ

t)h

117

118 Chaotic Modelling and Simulation

So any equilibrium point with a positive eigenvalue will be unstable. To determine

these eigenvalues, we need to compute the roots of the characteristic polynomial

A − λI



∂ ˙x

∂x

− λ

∂ ˙x

∂y

∂ ˙x

∂z

∂˙y

∂x

∂˙y

∂y

− λ

∂˙y

∂z

∂˙z

∂x

∂˙z

∂y

∂˙z

∂z

− λ



The matrix A − λI is called the characteristic matrix of the system.

6.2 The Lotka-Volterra Model

As an illustration of the above theory in a simpler case, let us consider a classical

two-dimensional system, the Lotka-Volterra model, also known as the predator-prey

model. In its simpliﬁed form, the Lotka-Volterra model has the form:

˙x = x − xy

˙y = −y + xy

(6.2)

In the terminology of Chapter 7, this is a conservative system with ﬁrst integral of

motion:

f (x, y) = xye

−x−y

It has two equilibrium points, at (x, y) = (0, 0) and at (x, y) = (1, 1). The characteris-

tic polynomial is given by



−y + 1 − λ −x

y x − 1 − λ



= λ

− (x − y)λ + (x + y − 1)

At (x, y) = (0, 0), the characteristic equation is

− 1 = 0

and the system has two real eigenvalues λ

1,2

= ±1. The eigenvectors correspond to

the two directions where there are no predators, and where there are no prey. Since

one of these eigenvalues is positive, the system is unstable. At (x, y) = (1, 1), the

characteristic equation is

+ 1 = 0

and the system has two imaginary eigenvalues, λ

1,2

= ±i. The system will cycle

around this point.

Using linearization, we see that near (0, 0), the system can be replaced by the

simpler system

˙x = x

˙y = −y

Three-Dimensional and Higher-Dimensional Models 119

whose orbits are the hyperbolas xy = c. Near (1, 1), if we use coordinates (ξ, η) =

(x − 1, y − 1) centred at 1, 1, the system can be replaced by the simpler system

ξ = −η

˙η = ξ

whose orbits are counterclockwise circles ξ

+ η

= (x − 1)

+ (y − 1)

= c.

6.3 The Arneodo Model

The simplest three-dimensional chaotic models are based on a system of three

linear diﬀerential equations, on which we add a non-linear term. An example of

such a system is the Arneodo model:

˙x = y

˙y = z

˙z = −



z + sy − mx + x



(6.3)

where s and m are parameters.

This model was proposed by Arneodo et al. (1979, 1980, 1981a), in their work on

systems that exhibit multiple periodicity and chaos. The Jacobian determinant of the

model is

J = −m + 2x.

There are two stationary (equilibrium) points, the origin (0, 0, 0), and (m, 0, 0).

In Figure 6.1, the (x, y) diagram of the system is shown (s = 3.8 and m = 7.5, the

initial values are (x

= 0.5 and y

= z

= 1). An integration method was used with

integration step d = 0.001.

A slight variation, replacing the last equation in (6.3) with

˙z = −



z + sy − mx + x



leads to a model with a more stable behaviour. Figure 6.2 shows the projections of

the three-dimensional solution path of this system to the three planes (x, y), (x, z) and

(y, z) respectively. The parameters are as above, except that m = 5. The bottom part

of this ﬁgure shows the chaotic oscillations in the (y, t) space.

The resulting paths of this modiﬁed system have a somewhat more complicated

form than those of (6.3). There are three stationary points:

( 0, 0, 0)

(

√

m, 0, 0)

(−

√

m, 0, 0)

(6.4)

The Jacobian of the modiﬁed system is J = −m + 3x

120 Chaotic Modelling and Simulation

FIGURE 6.1: The Arneodo model

FIGURE 6.2: A modiﬁed Arneodo model

Three-Dimensional and Higher-Dimensional Models 121

6.4 An Autocatalytic Attractor

Autocatalytic reactions often give rise to chaotic phenomena. The representation

of chemical reaction models by mathematical non-linear models is possible and has

been studied extensively (Prigogine and Lefever, 1968; Prigogine et al., 1969; Nico-

lis, 1971; Nicolis and Portnow, 1973; Nicolis and Prigogine, 1977, 1981; Nicolis

et al., 1983). It is more diﬃcult to ﬁnd a good representation of the numerous in-

termediate stages of a chemical reaction. The number of these stages inﬂuences the

complexity of the system, and, consequently, gives rise to a process with the chaotic

behaviour. Non-linear modelling theory suggests that at least one non-linear part

must be present in each reaction cycle in order for chaotic phenomena to appear.

A three-dimensional chaotic model is perhaps the simplest case, representing an

autocatalytic reaction with three stages. Such a model, for appropriate parameter val-

ues, may demonstrate chaotic behaviour, giving rise to a three-dimensional chaotic

attractor. A typical such model is given by the following system:

˙x = k + λz − x y

− x

˙y =

+ x − y

˙z = y − z

(6.5)

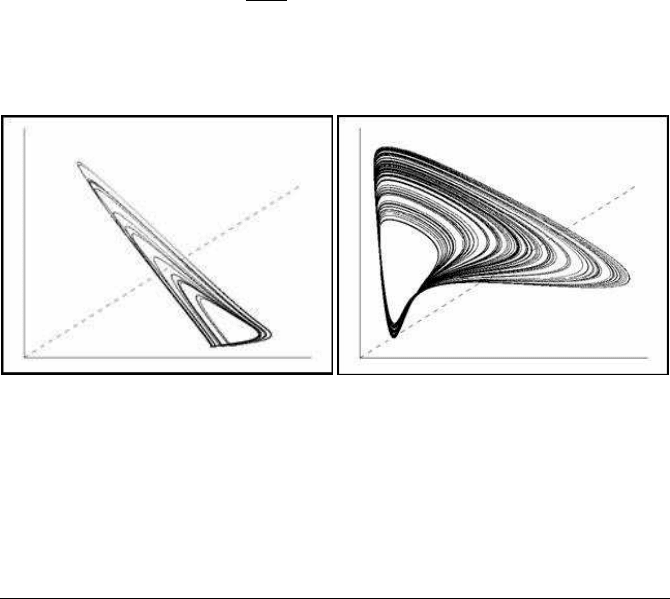
When the parameters of system (6.5) take the values k = 0.7567, λ = 0.3 and e =

0.013, Figure 6.3 arises. On the right side we see the two-dimensional (x, y) phase

portrait, while on the left side we see the temporal variation of chaotic oscillations in

the y direction (i.e. the (t, y) diagram).

FIGURE 6.3: An autocatalytic attractor

122 Chaotic Modelling and Simulation

A three-dimensional view (x, z, y) of the phase portrait of the autocatalytic reac-

tion is presented in Figure 6.4(a). The view from the (y, z, x) coordinate system is

presented in Figure 6.4(b). The parameters in both cases are k = 2.5, m = 0.017 and

e = 0.013, and the integration step is d = 0.0001. In this case the system (6.5) has

been modiﬁed slightly, with the ﬁrst equation replaced by:

˙x =

1 + k

+ m

(k + z) − xy

− x

(a) In the (x, z, y) coordinate system (b) In the (y, z, x) coordinate system

FIGURE 6.4: Three-dimensional views of the autocatalytic model

6.5 A Four-Dimensional Autocatalytic Attractor

The following four-dimensional model expresses a sequence of four chemical au-

tocatalytic reactions:

˙x

= x

− x

− 0.24x

+ 200x

+ a

˙x

= x

− x

− 10x

˙x

= 0.01 + 10x

− 20x

˙x

= 0.24x

− 100x

(6.6)

The non-linear character of (6.6) is due to the second order term in x

, which

appears in the ﬁrst and fourth equations, and to the couplings x

in the ﬁrst and the

Three-Dimensional and Higher-Dimensional Models 123

second equations and x

in the second and third equations. The control parameter,

a, has value −0.12, and the integration step is d = 0.003.

Figure 6.5(a) illustrates, from top to bottom, the (x

, t), (x

, t) and (x

, t) di-

agrams. The chaotic behaviour is similar, yet more complicated than in the previous

cases, whereas the time oscillations are of a purely chaotic nature, with several peaks

and intermediate chaotic stages. This is a very good example of chemical oscillations

and the related chaotic waves. Figure 6.5(b) shows the three-dimensional (x

, x

)

diagram representing the chaotic attractor of (6.6).

(a) Temporal chaotic oscillations (b) The (x

, x

) diagram

FIGURE 6.5: A four-dimensional autocatalytic model

6.6 The R¨ossler Model

One of the simplest three-dimensional models is the R¨ossler model (see R

ossler,

1976d):

˙x = −y − z

˙y = x − ez

˙z = f + xz − mz

(6.7)

The model contains a single non-linear term, xz, which enters in the third equation,

and three parameters, e, f and m.

Figure 6.6(a) is a three-dimensional view of the R

ossler model when the para-

meters are: e = 0.2, f = 0.2 and m = 5.7. Figure 6.6(b) shows, from left to right,