Skiadas C.H., Skiadas C. Chaotic Modelling and Simulation. Analysis of Chaotic Models, Attractors and Forms

Подождите немного. Документ загружается.

134 Chaotic Modelling and Simulation

(b) Compare the behaviour of the system to that of the system:

˙x = y

˙y = −sin(x)

and examine the resulting systems.

(d) What is the diﬀerences when we use the third-order Taylor approxima-

tion for sin(x)?

7. Let b > 0. Find the ﬁxed points of the system

˙x = y

˙y = −bx(x − 1)

and determine the stability of the system at the points.

8. Compute the eigenvalues of the Lorenz model.

9. Consider the system:

˙x = a − (b + 1)x + x

˙y = bx − x

(a) Find the equilibrium points of the system.

(b) Determine the system’s stability at these points.

10. Show that when c − ab > 0, equation (6.12) has at least one positive root.

11. Determine if the equilibrium points M

, M

−

for the Lorenz model, given by

equation (6.19), are stable.

12. Explain the butterﬂy eﬀect.

Chapter 7

Non-Chaotic Systems

In this chapter we discuss various aspects of non-chaotic systems, that will be helpful

in analysing other, more complex, systems. In section 7.1 we deﬁne conservative and

Hamiltonian systems, while in section 7.2 we give a brief account of linear systems

of diﬀerential equations, and the qualitative behaviour of their solutions near the

equilibrium point. These are models for the local behaviour of more complicated

systems near their equilibrium points.

In the remaining sections, we look at a number of interesting conservative systems.

7.1 Conservative Systems

In this section we consider two-dimensional conservative systems, that is, systems

that have a non-trivial ﬁrst integral of motion. For a system

˙x = F(x, y, t)

˙y = G(x, y, t)

(7.1)

A ﬁrst integral of motion is a function f (x, y), of x and y, that is independent of time.

As a consequence:

f (x, y) = ˙x

∂ f

∂x

+ ˙y

∂ f

∂y

= 0 (7.2)

There is a direct connection between the level curves of the ﬁrst integral and the

trajectories of the system: If f is a ﬁrst integral of the system (7.1), then f is constant

on every trajectory of the system. Thus, every trajectory is part of some level curve

of f , determined by the value of f at the initial conditions (x

, y

). Hence, each level

curve of f is a union of trajectories.

The ﬁrst integral derives its name from the usual method of computing it, by direct

integration of the diﬀerential equation:

(7.3)

This follows from (7.2), as follows. We consider a particular level curve of f ,

f (x, y) = c, and consequently we think of f as an implicit equation for y as a function

135

136 Chaotic Modelling and Simulation

of x. In that case, we have

∂ f

∂x

∂ f

∂y

= 0

which gives us:

f (x, y) = ˙x

∂ f

∂x

+ ˙y

∂ f

∂y

= −˙x

∂ f

∂y

+ ˙y

∂ f

∂y

∂ f

∂y

−˙x

+ ˙y

(7.4)

Equating the last term to zero, and using equation (7.1), we end up with equa-

tion (7.3). The value of the integration parameter is directly related to the level

of the curve.

Since F, G in general depend on t, this integral may not be independent of t. How-

ever, in the case where F, G are independent of the time t, integration of (7.3) will

result in a ﬁrst integral of motion for the system. We will examine a number of

particular such systems in this chapter.

Before we proceed, let us elaborate a bit more on the equations. As we saw

in (7.2), the ﬁrst integral of motion, f (x, y), and consequently the implicit equations

for the trajectories of the system, are determined by the equation:

∂ f

∂x

+ G

∂ f

∂y

= 0 (7.5)

Note that this equation will remain true if F, G are both multiplied by the same

function of x, y. To see this geometrically, notice that the trajectories are determined

completely by the direction of their tangent vector at any point, and this direction is

that of the vector ( ˙x, ˙y) = (F, G). Therefore, multiplying both F, G with the same

factor has no eﬀect on this direction.

This means that there is a family of conservative systems sharing the same ﬁrst in-

tegral of motion. From all these systems, there is one that stands out. Note that (7.5)

can be rewritten as:

∂ f

∂y

= −

∂ f

∂x

Rescaling F, G amounts to selecting a value for this ratio, so a natural choice would

be to set it to 1, in which case F, G, and hence the solutions of the system, are

completely determined from f by:

F =

∂ f

∂y

and G = −

∂ f

∂x

(7.6)

In this case, we will call f the Hamiltonian of the system, and we will call the

system a Hamiltonian system. All the systems we will consider in this section are

Hamiltonian.

Equations (7.6) provide a necessary condition for the Hamiltonian to exist, since

they imply that:

∂F

∂x

= −

∂G

∂y

∂

∂x∂y

Non-Chaotic Systems 137

In the case where F, G are independent of t, this is also suﬃcient, and the Hamilto-

nian can be computed by simply solving the system (7.6).

Hamiltonian systems play a central role in Hamiltonian Mechanics. The equations

of motion of Hamiltonian systems can be completely described using their Hamilto-

nian, from equations (7.5) and (7.6).

7.1.1 The simplest conservative system

The simplest conservative system is given by

˙x = y

˙y = −x

(7.7)

The corresponding diﬀerential equation for the integral of motion is

= −

(7.8)

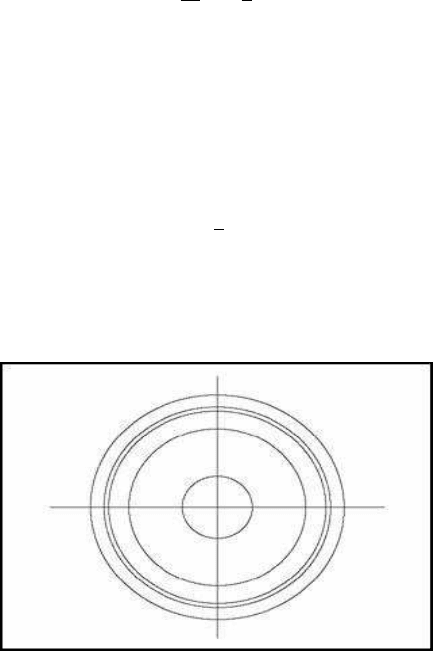
The solutions to (7.8) are concentric circles

+ y

= h

where h is a positive constant (Figure 7.1). Consequently, the system is conservative.

Its ﬁrst integral of motion is:

H(x, y) =



+ y



The level curves are therefore concentric circles, whose radius is determined by the

initial conditions (x

, y

FIGURE 7.1: The simplest conservative system

138 Chaotic Modelling and Simulation

Note that this is indeed a Hamiltonian system, as:

∂H

∂y

= y = ˙x and −

∂H

∂x

= −x = ˙y

We could have come to the same conclusions by solving the system:

∂H

∂x

= ˙x = y

∂H

∂y

= −˙y = x

Integrating the ﬁrst equation would yield H(x, y) =

+ c(x), and substituting into

the second equation would yield c(x) =

+ c.

7.1.2 Equilibrium points in Hamiltonian systems

Before we proceed to more complicated examples, it is worthwhile discussing

the behaviour of a system in a neighbourhood of an equilibrium point. Equilibrium

points are found by setting ˙x and ˙y to 0. In the case of a Hamiltonian system, this

corresponds to

∂H

∂x

∂H

∂y

= 0

So the equilibrium points of a Hamiltonian system are precisely the critical points of

the Hamiltonian H. For instance, in the system 7.7 the origin is the only equilibrium

point.

If (x

, y

) is an equilibrium point, then the Taylor expansion of H around (x

, y

)

will be:

H(x, y) = H(x

, y

) +

(x − x

)

+ h

(x − x

)(y −y

) +

(y −y

)

+ ··· (7.9)

where

∂

∂x



, y



, h

∂

∂x∂y



, y



, h

∂

∂y



, y



are the second-order partial derivatives of H at (x

, y

), and the terms ignored are

of higher order in x − x

, y − y

. If, for simplicity, we change coordinates so that

, y

) = (0, 0), and we further denote h

= H(x

, y

) = H(0, 0), then the equa-

tion (7.9) becomes:

H(x, y) = h

+ h

xy +

+ ···

Non-Chaotic Systems 139

So, the behaviour of the trajectories of the system, i.e. of the level curves of H, near

the equilibrium point, is determined by the quadratic form:



+ 2h

xy + h



(7.10)

Depending on the number of real roots of the characteristic polynomial

k(X) =

+ 2h

X + h

, these trajectories may look elliptic, hyperbolic, or parabolic.

If k(X) has no roots, then the trajectories near the equilibrium point are elliptical,

and the point is a stable equilibrium point. If k(X) has two distinct roots, then the

trajectories are hyperbolas, and their asymptotes are the lines with slopes the two

roots (this will be elaborated further in the next section).

For instance, the system (7.7) has an equilibrium point at (0, 0), whereupon H is

written, locally, as:

In this case, the polynomial in question is 1 + X

, which has no real roots. Hence,

the system will exhibit elliptical orbits near (0, 0).

7.2 Linear Systems

Near an equilibrium point (we will assume this point is 0, 0), system (7.1) can be

approximated by a linear system:

˙x = ax + by

˙y = cx + dy

(7.11)

where a, b, c and d are real numbers or, in a more general analysis, real functions of

t of a special form.

We will now discuss in greater detail the classical theory of system (7.11). This

system has, as already mentioned, an equilibrium point at (x, y) = (0, 0). We will

This quadratic form is the quadratic form associated to the Hessian matrix:







∂

∂x

∂

∂x∂y

∂

∂y∂x

∂

∂y







This number depends of course on the discriminant of the polynomial, which is the determinant of

the Hessian matrix.

That is, in the case that the critical point is non-degenerate, i.e. in the case where the characteristic

polynomial is not identically zero.

In this case, of course, the orbits will remain elliptical even away from 0, 0.

140 Chaotic Modelling and Simulation

denote by A the matrix of coeﬃcients:

A =

a b

c d

The eigenvalues of this matrix are called the eigenvalues of system (7.11), and

they are given by the equation

A − λI



a − λ b

c d − λ



= 0

or, in simpler terms:

− (a + d)λ + (ad − bc) = 0

If we note, that a + d and ad − bc are respectively the trace and determinant of A,

we can write the equation for the eigenvalues as:

− tr(A)λ + det (A) = 0

The solutions to this are

1,2

tr(A) ±

√

∆

(7.12)

where, as usual, ∆ denotes the discriminant:

∆ = tr(A)

− 4 det(A) (7.13)

Before we proceed to a classiﬁcation of equilibrium points according to the qual-

itative behaviour of the solutions near these points, we will discuss the eﬀects of

various transformations on the shape of the matrix A.

7.2.1 Transformations on linear systems

We start by considering a simple coordinate rescaling:

u = kx v = k

′

(7.14)

The transformed system (7.11) then takes the form

˙u = au + rbv

˙v =

cu + dv

where r =

′

. So the matrix of the new system, A

′

, is:

′

a rb

c d

Non-Chaotic Systems 141

The trace and determinant thus remain invariant:

tr(A

′

) = tr(A)

det(A

′

) = det(A)

A more general change of coordinates amounts to the transformation

u v

= C

x y

(7.15)

where C is an invertible matrix of constants. The corresponding matrix A

′

is then a

matrix similar to A:

′

= CAC

′

Hence, this again keeps the trace and determinant invariant.

Another simple transformation involves time rescaling:

u(t) = x(kt) v(t) = y(kt)

(7.16)

System (7.11) then becomes:

˙u = kau + kbv

˙v = kcu + kdv

Thus the matrix of the system becomes

′

= kA

and hence

tr(A

′

) = k tr(A)

det(A

′

) = k

det(A)

According to (7.12) and (7.13), the eigenvalues are simply rescaled by k.

Finally, the transformation

u(t) = e

−kt

x(t) v(t) = e

−kt

y(t)

(7.17)

results in a system with matrix

′

= A − kI

with the corresponding changes this implies to the trace and determinant:

tr(A

′

) = tr(A) − 2k

det(A

′

) = k

− k tr(A) + det(A)

Note however, that this transformation does keep the discriminant

∆ = tr(A)

− 4 det(A)

invariant, and hence it amounts to a parallel translation of the eigenvalues by −k.

This transformation changes radically the behaviour of solutions near (0, 0), but in a

very controlled way, and we will utilise it in the next section.

This does not alter in any essential way the behaviour of solutions near the point (0, 0), provided

k > 0.

142 Chaotic Modelling and Simulation

7.2.2 Qualitative behaviour at equilibrium points

We will now proceed to analyse the qualitative behaviour of solutions near equi-

librium points, using the transformations from section 7.2.1. First oﬀ, the sign of

tr A is of paramount importance. Using transformation (7.17), we can always reduce

to the case where tr(A) = 0, i.e. where d = −a, and we will do so for the next couple

of paragraphs. The condition tr(A) = 0 is exactly the condition for system (7.11) to

be conservative. In that case, the system has the ﬁrst integral:

f (x, y) = cx

− 2axy − by

We have to distinguish a couple of cases here.

1. ∆ = 0, i.e. the ﬁrst integral f is degenerate, and there is only one, double,

eigenvalue, namely 0. Up to a change of coordinates, we may assume f (x, y) =

, i.e. that the linear system is:

˙x = 0

˙y = x

The solutions are then:

x(t) = A

y(t) = At + B

This case is illustrated in Figures 7.2(a) and 7.2(b).

2. ∆ < 0. Then, there are two complex eigenvalues, which, after performing

transformation (7.16), we may assume to be ±i. Then, up to a change of

coordinates, we may assume f (x, y) = x

+ y

, i.e. that the linear system

˙x = −y

˙y = x

The solutions are then:

x(t) = A cos(t) + B sin(t)

y(t) = B cos(t) − A sin(t)

This case is illustrated in Figures 7.2(c) and 7.2(d).

3. ∆ > 0. Then there are two distinct real eigenvalues, which, after performing

tranformation (7.16), we may assume to be ±1. After a change of coordinates,

we may assume that f (x, y) = xy, i.e. that the system is:

˙x = x

˙y = −y

The solutions are then:

x(t) = Ae

y(t) = Be

−t

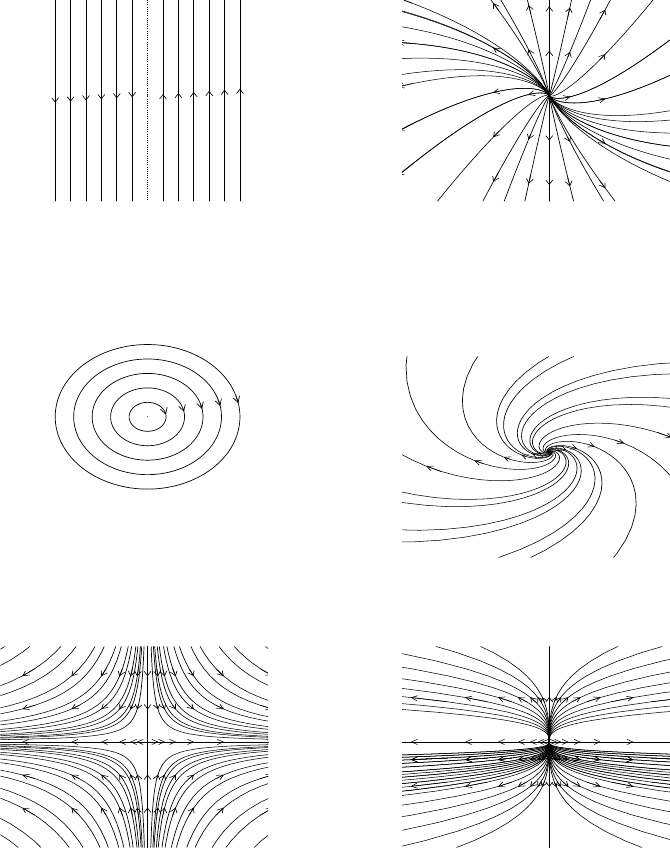
Non-Chaotic Systems 143

(a) ∆ = 0 , tr(A) = 0 (b) ∆ = 0, tr(A) > 0

(e) Saddle point, ∆ > 0, tr(A) = 0 (f) ∆ > 0 , tr(A) > 0

FIGURE 7.2: Qualitative classiﬁcation of equilibrium points