Skiadas C.H., Skiadas C. Chaotic Modelling and Simulation. Analysis of Chaotic Models, Attractors and Forms

Подождите немного. Документ загружается.

94 Chaotic Modelling and Simulation

(a) The bifurcation diagram (a, x) (b) A carpet-like map

FIGURE 4.15: Carpet-like forms

(a) A carpet-like pattern (b) Groups of square-forms

FIGURE 4.16: Carpet-like forms

The Delay Logistic Model 95

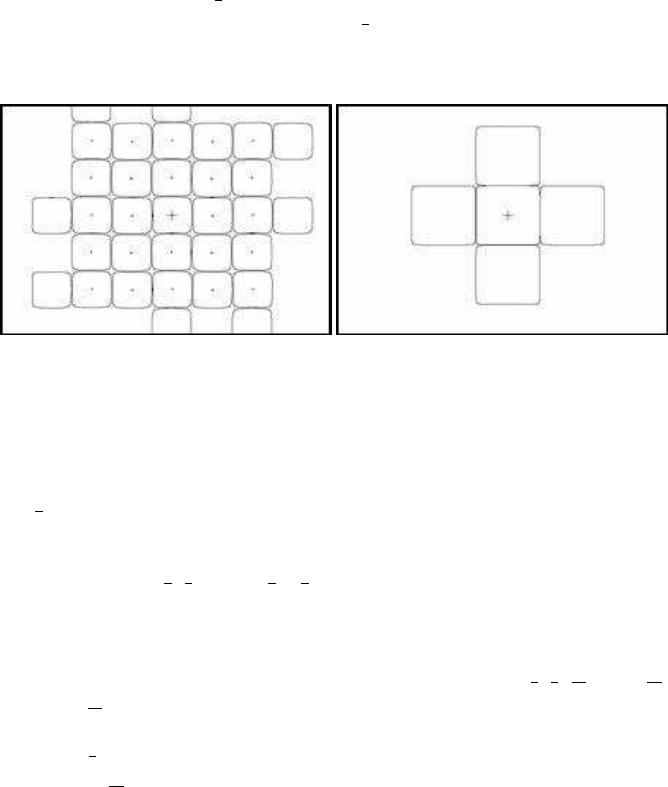
Figure 4.17(a) illustrates the same map as in Figure 4.16(b), but in the latter case

only the centers and the corresponding squares are present. When the control para-

meter is very small, a = 0.01, almost perfect squares appear. This is illustrated in

Figure 4.17(b). The chaotic sea almost disappears and the non-symmetric islands

become geometric objects. The original central square is drawn (starting with an

initial value a bit less than

), along with the ﬁrst group of four surrounding squares

(starting with an initial value a bit more than

(a) Square-like forms (b) The generating squares

FIGURE 4.17: Square-like forms

The case of b = 1 is illustrated in Figure 4.18(a). The control parameter here is

a =

. The building blocks for the construction of the above carpet-like form are two

interrelated objects close to the origin (marked by a cross in Figure 4.18(b), where a

was set to 0.001). The two forms have the shape of almost perfect squares, with their

centers located at (−

) and at (

, −

The bifurcation diagram (b, x) appears in Figure 4.19(a). Period doubling and to-

tally chaotic regions are clearly present. At the end of the diagram the chaotic region

has a stochastic character. The oscillations seem to cover the entire plane. Interesting

windows and special forms appear when a takes the special values

2π

, π and

3π

The value

3π

is the lower limit for the control parameter a. Beyond it, the chaotic

sea covers the entire plane, with no islands present. Figure 4.19(b) shows the case

where a =

. On the outer part of each pattern we can see 6 small islands.

When a =

2π

the ﬁxed point bifurcates into a period-2 orbit. This is illustrated in

Figure 4.19(c). The six islands from the preceding case are now separated from the

original form, and are inside the chaotic sea. On the boundary one can now see 4

islands. The system is at the starting point of the bifurcation. In Figure 4.19(d) the

bifurcation has been completed, and two distinct chaotic objects appear. The control

parameter at this point is a = π.

When the control parameter is increased, a triangular form appears (Figure 4.20(a),

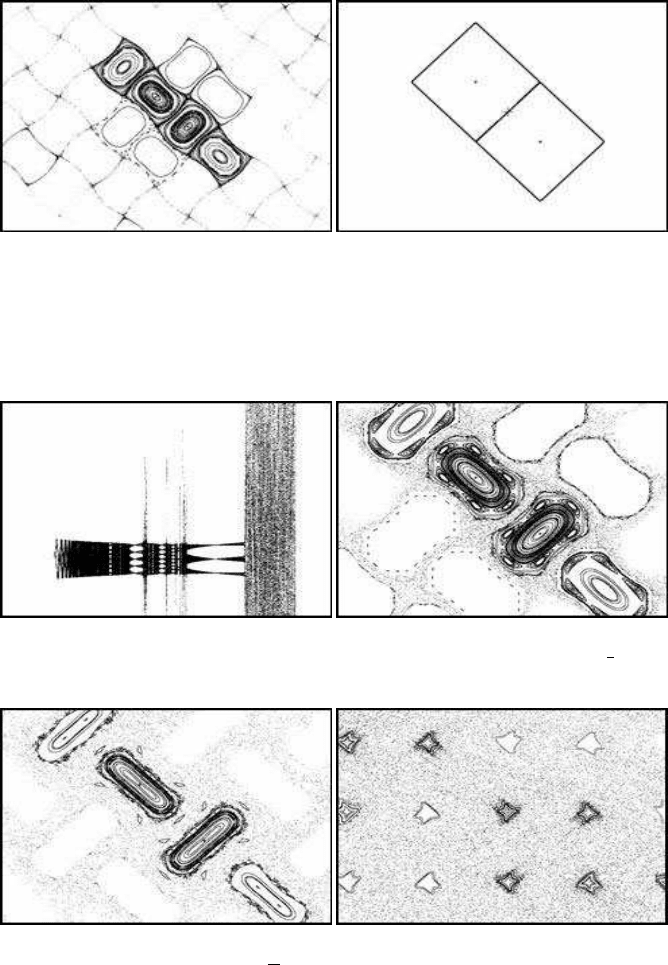
96 Chaotic Modelling and Simulation

(a) Irregular patterns (b) The generating squares

FIGURE 4.18: Irregular patterns

(a) Bifurcation diagram (b, x) (b) Islands in the chaotic sea, a =

2π

(d) The order-2 bifurcation

FIGURE 4.19: Islands in the chaotic sea

The Delay Logistic Model 97

a =

6π

−0.008). When a gets closer to

6π

, the triangular form splits into three objects

around the central one (Figure 4.20(b), a =

6π

− 0.02).

(a) A triangular island (b) An order-3 bifurcation

FIGURE 4.20: Triangular islands

The H

enon model was introduced here in order to compare it to the other delay

models. However, the H

enon model is a very interesting model, deserving its own

study. A more detailed analysis of the H

enon model will be the subject of the next

chapter.

98 Chaotic Modelling and Simulation

Questions and Exercises

1. Determine the sides of the large hexagon appearing on the right of Figure 4.1.

2. Draw the (x

t−m

, x

t+1

) and (t, x

t+1

) graphs for the Gompertz delay model and for

various positive values of the parameters a, b and m.

3. Draw the graph of the same model for m = 40, a = 0.9 and b = 0.28, and

compare the resulting ﬁgure with that of the Glass and the logistic models.

4. Replace the cos(x

) term into the delay cosine map (Equation (4.22)) by Taylor

approximation to the cosine

cos(x

) = 1 −

and draw the bifurcation diagram for b = −1 and compare the resulting ﬁgure

with that provided for the delay cosine model. Find the characteristic points

and compare them to those of the delay cosine.

5. Repeat the analysis and graphs of the previous problem, but now for the delay

map

t+1

= −x

t−1

+ a

1 −

where c is a positive parameter. Find similarities and diﬀerences with the

previous case.

6. Find the Jacobian of the map in the previous problem, and generalise your

result to a map of the form

t+1

= −x

t−1

+ a f (x

)

where f (x

) is a continuous smooth function.

7. Can you draw carpet like forms by using the map resulting from the approxi-

mation of the cosine? Justify your answer.

8. What happens to the number of “folds” in Figure 4.4(b) as the delay parameter

m increases?

9. Examine what happens when the parameter b in (4.8) is allowed to take non-

integer values.

Chapter 5

The H´enon Model

The H

enon model is a two-dimensional model introduced and analysed by H

enon

(1976). This model can also be expressed by a delay diﬀerence equation:

t+1

= bx

t−1

+ 1 − ax

(5.1)

By introducing a new variable, y

= x

t+1

, (5.1) is transformed into a system of two

ordinary diﬀerence equations:

t+1

= y

+ 1 − ax

t+1

= bx

(5.2)

The Jacobian determinant of (5.2) is given by:

det J =



∂x

t+1

∂x

t+1

∂y

t+1

∂x

∂y

t+1

∂y



= −b

When b = 1, the resulting map is area preserving, but the system is unstable. The

system becomes stable for 0 < b < 1. A variety of maps appear when a and b vary

over a range of values, and the resulting maps take the form of chaotic attractors.

We will see a variety of these attractors in this chapter. The most known chaotic

attractor of the H

enon model appears when a = 1.4 and b = 0.3, and is illustrated in

Figure 5.1.

5.1 Global Period Doubling Bifurcations in the H´enon

Map

Global period doubling bifurcations in the H

enon map have been studied by many

researchers, and a very detailed analysis can be found in Murakami et al. (2002).

The analysis of the H

enon map is based on (5.1) and (5.2). The ﬁxed points (x

t+1

, y

t+1

= y

) of the map are the solutions of the second-order polynomial:

− (b − 1)x − 1 = 0

namely

(b − 1) ±

(b − 1)

+ 4a

, y

= x

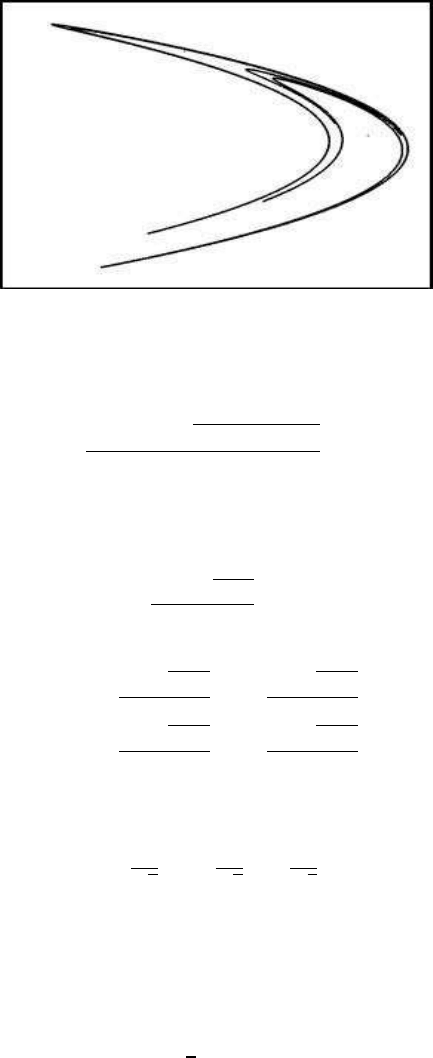
100 Chaotic Modelling and Simulation

FIGURE 5.1: The H

enon map

The period-2 orbit can be found from the relations x

t+2

= x

and y

t+2

= y

. The

resulting fourth-order equation for x has the two extra solutions

−(b − 1) ±

−3(1 − b)

+ 4a

, y

= x

5.1.1 Period doubling bifurcations when b = −1

When b = −1, the map has the stable ﬁxed point

−1 +

√

1 + a

, y

= x

for −1 < a < 3. This turns into the period-2 orbit

1 +

√

a − 3

, y

1 −

√

a − 3

1 −

√

a − 3

, y

1 +

√

a − 3

(5.3)

at the value a = 3. This orbit remains stable for 3 < a < 4. The second period

doubling takes place at a = 4, giving rise to the period-4 orbit with

√

, y

√

1 −

√

1/2

= −y

, y

= x

, y

= −y

= y

, y

= x

(5.4)

The third period doubling bifurcation takes place when a = 4.12045, giving rise

to a period-8 orbit. This last value of a is the root of:

4a(2

√

a − a) + 1 = 0

The H´enon Model 101

5.1.2 Period doubling bifurcations when b = 1

When b = 1, the ﬁxed points of (5.2) are at

x = ±

√

, y = x (5.5)

These are both unstable when a > 0. The period-2 orbit consists of the points

x = ±

√

, y = −x

This orbit becomes unstable when a = 1, and we have a bifurcation into a period-4

orbit. The period-4 orbit undergoes a period doubling bifurcation at a =

8−

√

1.13397 and leads to a period-8 orbit. The period-8 orbit bifurcates into the period-

16 orbit at a = 1.15135. We leave the details to the reader.

5.2 The Cosine-H´enon Model

During the simulation process related to the global period doubling bifurcation,

diﬃculties arise on the estimation of the starting parameters, as well as of the local

or global instabilities related to the period doubling. It is, therefore, more convenient

to use an analogue of the H

enon system, based on trigonometric functions:

t+1

= by

+ 2a

(

cos

(

)

− 1

)

+ 1

t+1

= x

(5.6)

This model is called the cosine H´enon model. The relation between the two models

is that the H

enon model (5.2) is the model obtained from (5.6) when the cosine term

is replaced by its second-order Taylor approximation:

cos(x

) = 1 −

Therefore, this new model retains many of the properties of the H

enon model,

but it also has other distinct properties. This model accepts a wider range of initial

values in the (x, y) plane. Furthermore, the values of the control parameter related

to the period doubling bifurcations of the H

enon map are close to the corresponding

values of the control parameter for the cosine model (b = −1). The ﬁxed point at

the critical value a = 3 is illustrated in Figure 5.2(a). Also present in this case are 7

islands on the boundary. Figure 5.2(b) illustrates the period-2 orbit at a = 3.23. The

system is in sub-critical state, just before the completion of the next global period

doubling. We can see 11 islands on the boundary.

Figure 5.2(c) illustrates the period-4 orbit of the cosine map with b = −1 and

a = 4.11.

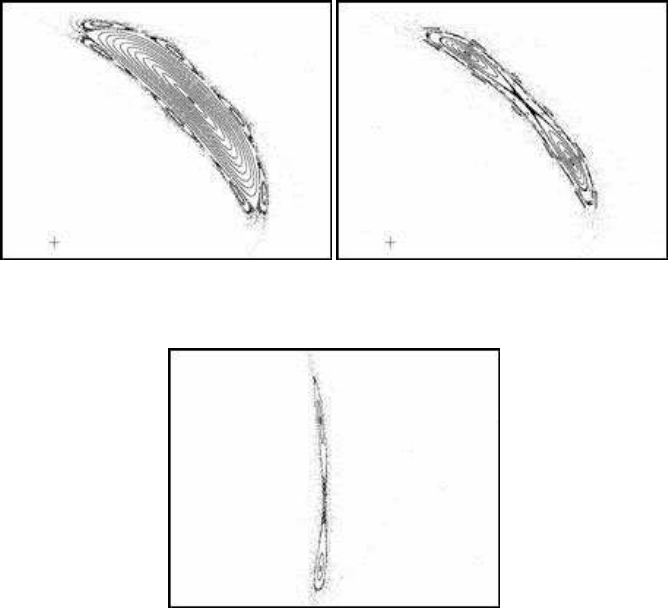
102 Chaotic Modelling and Simulation

(a) The ﬁxed point (a = 3) (b) The period-2 orbit

FIGURE 5.2: Orbits in the cosine H

enon model

The H´enon Model 103

5.3 An Example of Bifurcation and Period Doubling

Figures 5.3(a) and 5.3(b) illustrate some interesting cases regarding the bifurcation

and period doubling when the parameter b of the cosine H

enon model takes the

value b = 1. The system will undergo period doubling when a = 1. Figures 5.3(a),

5.3(b), 5.4(a) and 5.4(b) show the map when the control parameter is a = 0.8, 0.98,

1.02 and 1.3 respectively. In Figure 5.3(a), a double structure appears. After the

period doubling, we see that, in each of the original structures, the central island has

turned into three separate forms. In Figure 5.4(b), the period-4 islands are completely

separated.

(a) a = 0.8 (b) a = 0.98

FIGURE 5.3: Bifurcation forms in the cosine H

enon model

5.4 A Diﬀerential Equation Analogue

A diﬀerential equation analogue to the H

enon model is given by the following

system of two coupled diﬀerential equations

˙x = by + 1 − ax

− x

˙y = x − y

(5.7)