Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

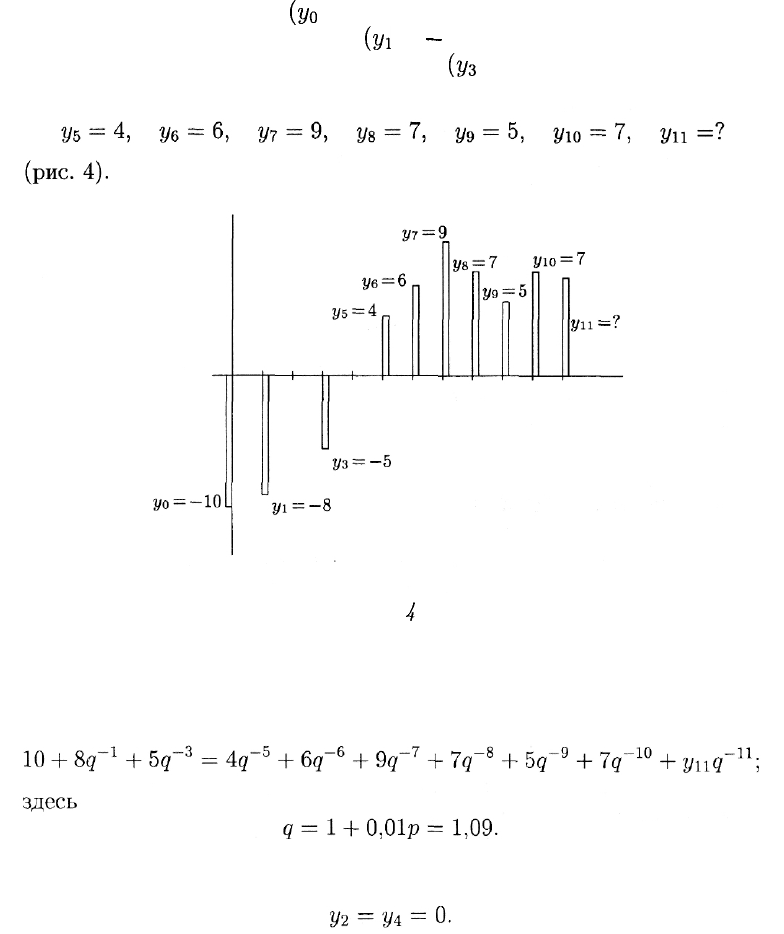
5.3. БАЛАНСОВОЕ РАВЕНСТВО

5.3. Балансовое равенство

Рассмотрим задачу посложнее.

Пример 3. Предположим, что заемщик берет кредит по частям

у одного и того же кредитора под 9% годовых:

сразу — 10 млн. руб.

(г/о

= —10),

через год — еще 8 млн. руб.

(у\

—

и еще через два года — 5 млн. руб.

(у

= —5),

а схема погашения кредита выглядит так:

Рис.

Дисконтируя все суммы на момент выдачи первой части креди-

та и приравнивая суммы, соответствующие кредитам и погашениям,

получаем:

Перепишем последнее соотношение формально более подробно,

имея в виду, что

131

ГЛАВА 5. БАЛАНСОВОЕ УРАВНЕНИЕ

6<T

9q-

7q'

7q~

= 0.

После необходимых вычислений находим

Уп

— 6,7 млн. руб.

Подведем некоторые итоги.

Пусть

— величина взноса в конце

А>го

года,

к ^ 0 (отрицатель-

ное значение

трактуется как кредит).

Все кредиты погашены за п лет, если имеет место балансовое ра-

венство

Уо

+ q"

y\ +

•••

+ q"

= 0, (1)

где

q = l + 0,01p,

т. е. сумма всех дисконтированных кредитов и взносов равна нулю.

При этом р% называют нормой

процента,

или ставкой дисконта,

или нормой дисконта.

5.4. Балансовое уравнение

Метод дисконта можно использовать для оценки экономической эф-

фективности вариантов капитальных вложений.

Пусть

уь

— известные нам доходы предприятия за

k-Vi

год (от-

рицательное значение

трактуется как капитальное вложение) в

проекте, рассчитанном на п лет.

Используем равенство (1)

считая на этот раз, что величины

Уо,

yi,

• • •,

известны, а величина

q (а значит, и р) подлежит определению.

Соотношение (2) при этих условиях называется балансовым урав-

нением.

Индексом прибыльности, или внутренней нормой процента по

капвложениям, называется ставка дисконта, при которой сумма всех

132

5.4-

БАЛАНСОВОЕ УРАВНЕНИЕ

дисконтированных капитальных затрат и дисконтированных дохо-

дов равна нулю.

Обозначение: P.I. (сокращение от profitability index).

Тем самым, находя значение q = q*, удовлетворяющее уравнению

(2), мы определяем индекс прибыльности.

Обычная рыночная процентная ставка составляет примерно 8%.

Вложение считается выгодным, если

Итак, пусть

— обсуждаемый вариант капитальных затрат и ожидаемых доходов.

Для того чтобы найти P.I., составляем балансовое уравнение

Пусть q = q* — его решение. Тогда

Пример

Обсуждаемый вариант капитальных затрат и ожи-

даемых доходов показан на рис. 5, т. е.

Из последнего соотношения получаем, что

Тем самым,

133

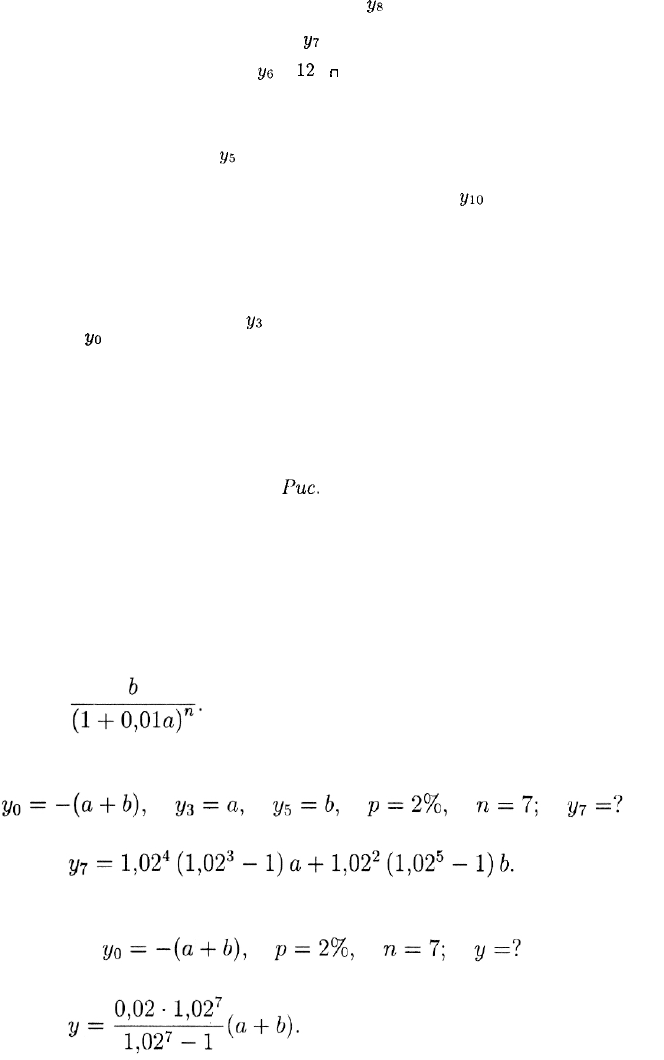
ГЛАВА 5. БАЛАНСОВОЕ УРАВНЕНИЕ

г/о

= -6

г/в

г/т

= 15

г/б

г/5

= 6

1/з

= -4

г/ю

= 4,79

Рис.

5.5. Задания и ответы

1. В банк под а% годовых была положена некоторая сумма. Через п

лет на счете оказалось b млн. руб. Каков размер положенной суммы?

Ответ:

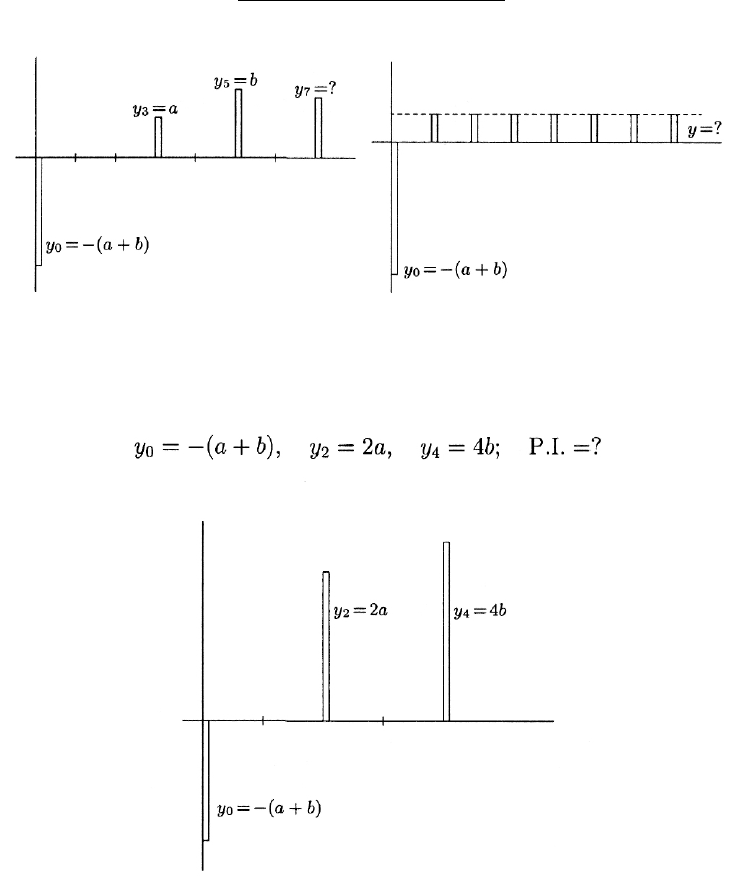
2. Условие задачи изображено на рис. 6:

Ответ:

3. Условие задачи изображено на рис. 7:

Ответ:

134

5.5. ЗАДАНИЯ И ОТВЕТЫ

Рис. 6

Рис. 7

4. Условие задачи изображено на рис. 8:

Рис. 8

Ответ: P.I. = 41%.

Глава 6

УПРАВЛЕНИЕ ЗАПАСАМИ

6.1. Вводные замечания

Фирмы часто делают различные запасы. Хранятся сырье, заготовки,

готовая продукция, предназначенная для продажи.

Запасов не должно быть ни слишком много, ни слишком мало.

В первом случае возникает необходимость неоправданных затрат на

хранение, на амортизацию товара. Во втором случае может оказать-

ся так, что на складе не будет нужного товара. Кроме того, малое

количество запасов подразумевает их частое пополнение, что также

требует затрат.

Задача управления запасами состоит в том, чтобы избежать обеих

крайностей и сделать общие затраты по возможности меньше. Отме-

тим, что в целом эта область науки управления развита довольно

хорошо, разработаны многочисленные модели с применением раз-

личных математических методов. Мы рассмотрим несколько прос-

тейших детерминированных моделей управления запасами.

6.2. Основная модель

Важнейшую роль в наших рассмотрениях будет играть функция из-

менения запаса. Это связь между количеством единиц товара на

складе (обозначим его через Q) и временем t. Будем считать, что

имеется один вид товара.

Если на товар имеется спрос, то функция изменения запаса

Q — Q(t) убывает. Если товар, наоборот, завозят на склад, то эта

136

6.2. ОСНОВНАЯ МОДЕЛЬ

функция возрастает. Мы будем считать возможным мгновенное по-

полнение запаса.

Затраты, связанные с запасами, можно разделить на три части.

Стоимость товара.

Б. Организационные издержки. Это расходы, связанные с офор-

млением товара, его доставкой, разгрузкой и т. д.

Издержки на хранение товара. Это затраты на аренду склада,

амортизацию в процессе хранения и т. д.

Рассмотрим основные величины и предположения относительно

них, принятые в рамках основной модели. Мы будем в основном ис-

пользовать в качестве единицы измерения денежных средств услов-

ные единицы (УЕ), это могут быть рубли, доллары и т. п.; в качестве

единицы измерения времени — год, хотя можно было бы взять ме-

сяц, квартал и т. п.

1. Цена единицы товара — с УЕ. Цена постоянна, рассматрива-

ется один вид товара.

2. Интенсивность

спроса—

d единиц товара в год. Будем считать,

что спрос постоянный и непрерывный.

3. Организационные издержки — s УЕ за одну партию товара. Бу-

дем считать, что организационные издержки не зависят от размера

поставки, т. е. от количества единиц товара в одной партии.

4. Издержки на хранение запаса — h УЕ на единицу товара в год.

Будем считать эти издержки постоянными.

5. Размер одной партии товара постоянен — q единиц. Партия

поступает мгновенно в тот момент, когда возникает дефицит, т. е.

когда запас на складе становится равным нулю.

При сделанных предположениях график функции изменения за-

паса будет таким, как показано на рис. 1: он состоит из повторя-

ющихся циклов пополнения запаса между двумя соседними дефи-

цитами. Вертикальные отрезки отвечают мгновенному пополнению

запаса.

Параметры с, d, s, h считаются заданными. Задача управления

запасами состоит в выборе параметра q таким образом, чтобы мини-

мизировать годовые затраты.

Для решения сформулированной задачи надо прежде всего выра-

зить эти затраты через параметры с, d, s, h, q.

А. Поскольку годовая интенсивность спроса равна d, а цена еди-

ницы товара — с, то общая стоимость товара в год равна

cd.

ЮЗак.

7492

^37

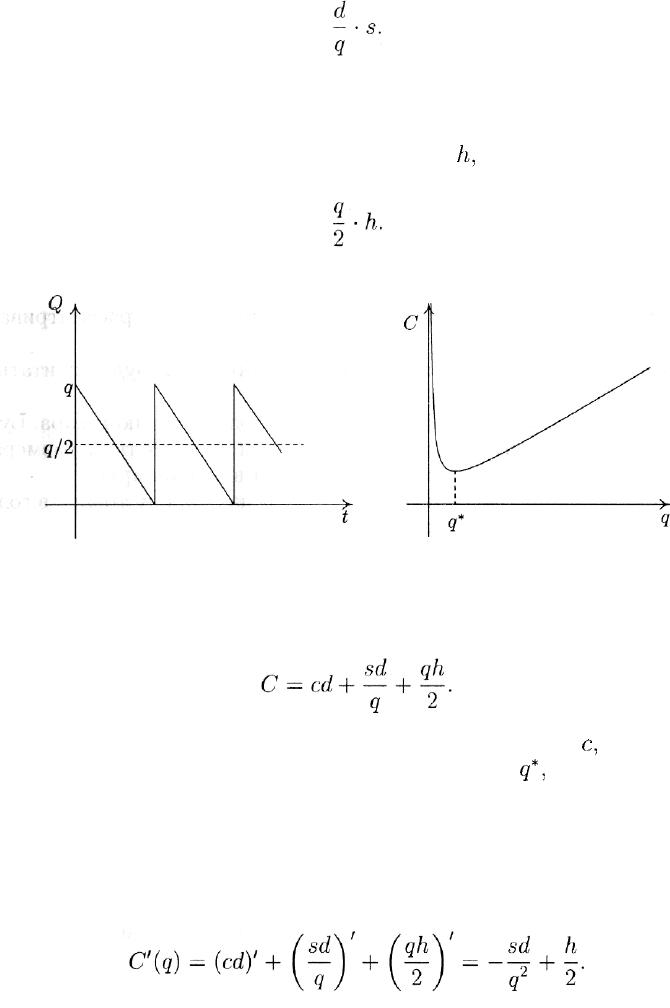
ГЛАВА 6. УПРАВЛЕНИЕ ЗАПАСАМИ

Б. Поскольку в одной партии q единиц товара, а годовой спрос

равен d, то число поставок равно d/q. В течение года организацион-

ные издержки равны

В. Средний уровень запаса равен отношению площади под гра-

фиком за цикл к продолжительности цикла. Этот средний уровень

равен q/2 (на рис. 1 обозначен пунктиром). Поскольку годовые из-

держки на хранение единицы товара равны

/г,

то общие издержки на

хранение составляют

Рис. 1 Рис. 2

Таким образом, общие издержки С вычисляются по формуле

Еще раз напомним, что в рамках модели параметры

с,

d, s, h счи-

таются заданными и требуется найти такое число

q*,

чтобы функция

С = C(q) принимала наименьшее значение на множестве q > 0 имен-

но в точке q*.

График функции С = C(q) показан на рис. 2.

Для нахождения точки q* минимума функции С — C(q) найдем

ее производную (с, d, s, h — фиксированные числа):

138

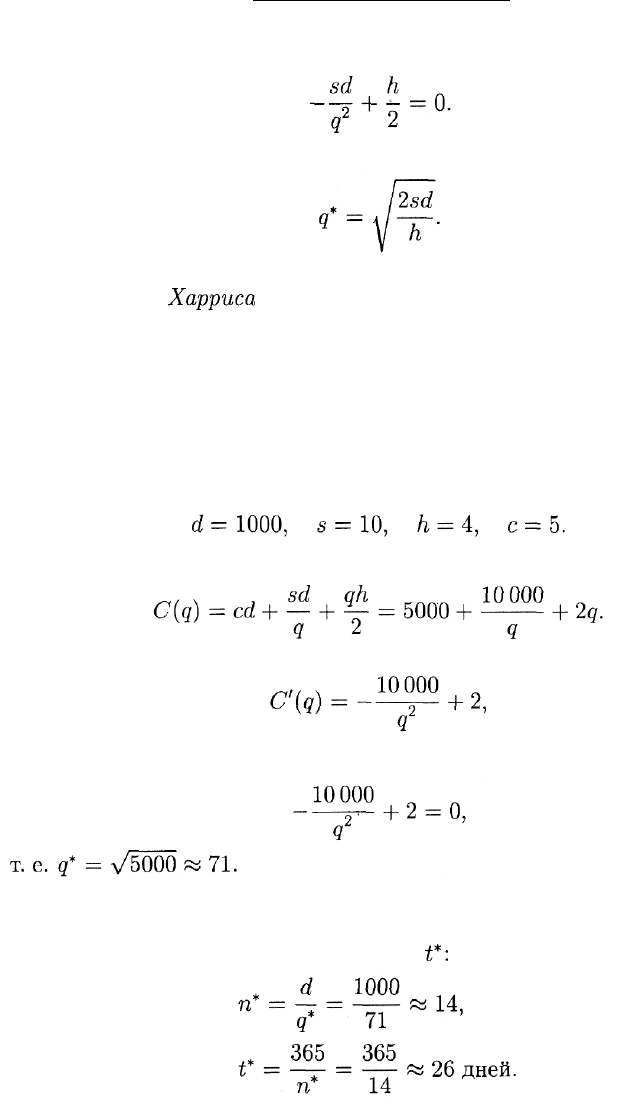
6.2. ОСНОВНАЯ МОДЕЛЬ

Приравнивая C'(q) к нулю, получаем

Отсюда можно найти q*. Имеем:

Полученная формула называется формулой оптимального запаса

или формулой

Харриса

(Harris).

Пример 1. Пусть интенсивность равномерного спроса состав-

ляет 1000 единиц товара в год. Организационные издержки равны

10 УЕ, издержки на хранение — 4 УЕ на единицу товара в год, цена

товара — 5 УЕ.

Определить оптимальный размер партии в предположении, что

система подчиняется основной модели.

Решение. Имеем:

Общие затраты равны:

Тогда

а оптимальный размер поставки q* является решением уравнения

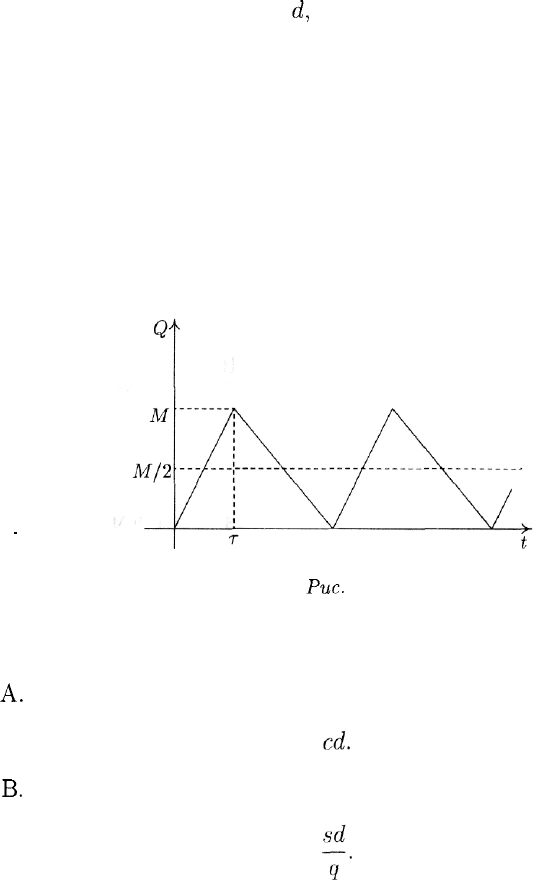
Замечание. Найдя оптимальный размер заказа, можно определить

оптимальное число поставок за год п* и соответствующую продол-

жительность цикла изменения запаса

£*:

ГЛАВА 6. УПРАВЛЕНИЕ ЗАПАСАМИ

6.3. Модель производственных поставок

В основной модели предполагалось, что поступление товаров на

склад происходит мгновенно. Это предположение достаточно хоро-

шо отражает ситуацию, когда товар поставляется в течение одного

дня (или ночи). Если товары поставляются с работающей производ-

ственной линии, необходимо модифицировать основную модель. В

этом случае к параметрам с,

s и h добавляется еще один — про-

изводительность производственной линии р (единиц товара в год).

Будем считать ее заданной и постоянной.

Эта новая модель называется моделью производственных поста-

вок. Величина q по-прежнему обозначает размер партии. В начале

каждого цикла происходит "подключение" к производственной ли-

нии, которое продолжается до накопления q единиц товара. После

этого пополнения запасов не происходит до тех пор, пока не возник

дефицит.

График функции изменения запаса имеет вид, изображенный на

рис. 3.

Рис.

Общие издержки C(q), как и в основной модели, состоят из трех

частей.

Общая стоимость товара в год равна

Годовые организационные издержки равны

140