Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

8.2. ПОСТАНОВКА ЗАДАЧИ

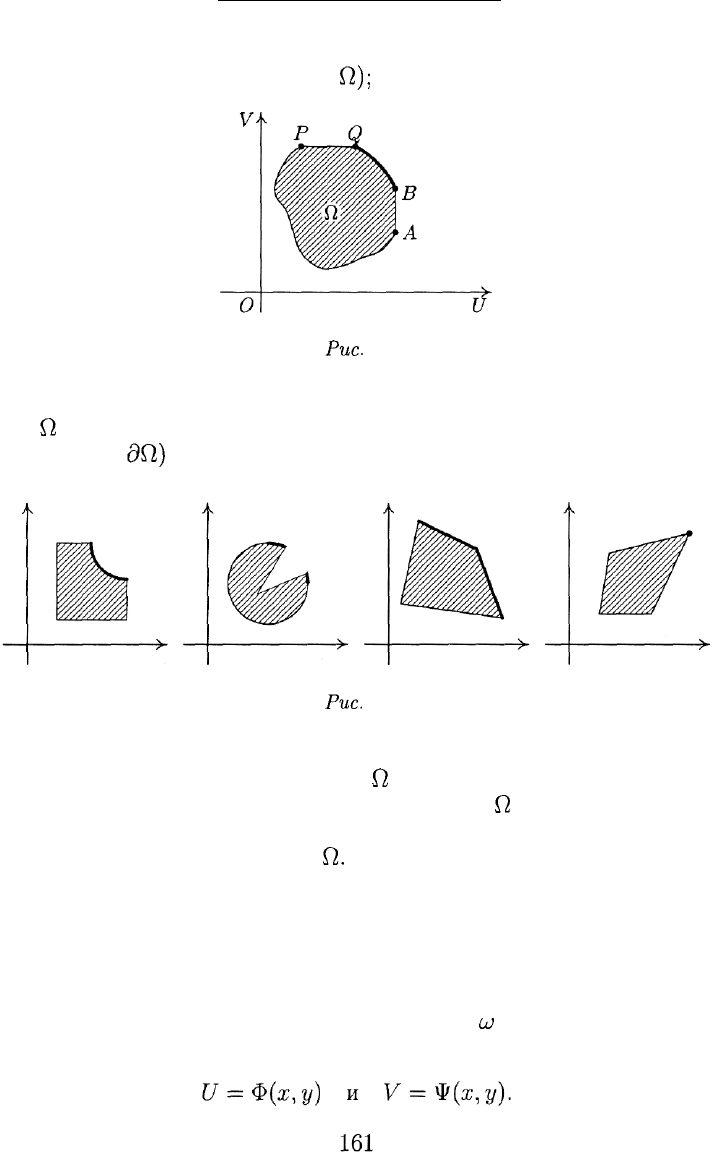
значения второй (вертикальный отрезок АВ и горизонтальный от-

резок PQ на границе множества

О,);

Рис.

в третий класс попадут точки, перемещение которых по множе-

ству

способно лишь уменьшить хотя бы одну из координат (дуга

BQ границы

dQ)

(рис. 5).

Рис.

Множество точек третьего класса называется границей (множе-

ством) Парето данного множества

(выделено на рис. 5).

Говоря нестрого, граница Парето множества

Г2

— это точки, из ко-

торых нельзя сдвинуться на "север", "восток" либо "северо-восток",

оставаясь в том же множестве

П.

На рис. б указаны границы Парето некоторых множеств.

8.2. Постановка задачи

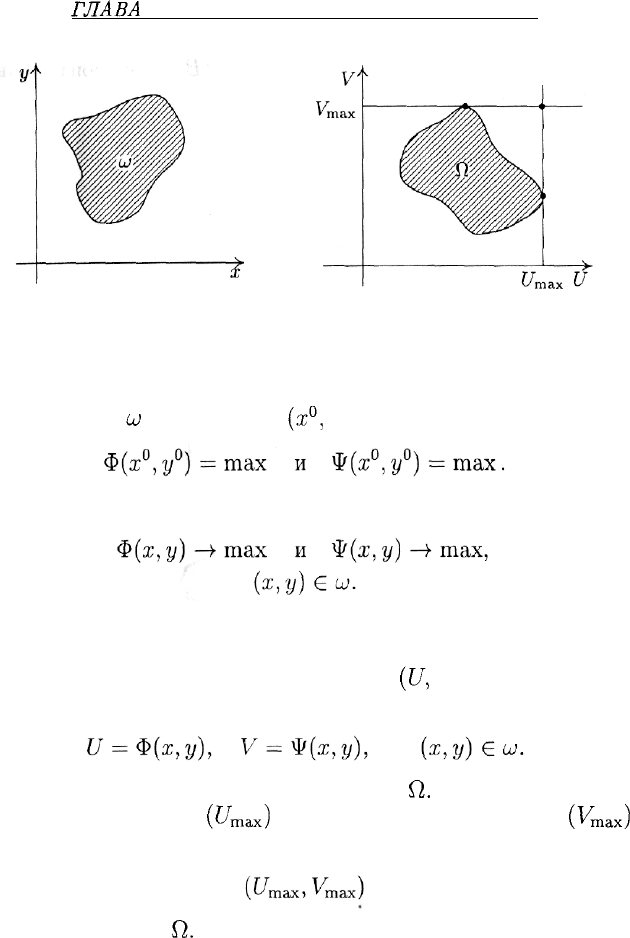
Пусть на плоскости (х, у) задано множество

(рис. 7) и в каждой

точке этого множества определены две непрерывные функции:

ГЛАВА

8. МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ

Рис. 7

Рис. 8

Рассмотрим следующую задачу.

На множестве

найти точку

(ж

), в которой

Обычно это записывается так:

Сразу же отметим, что в общем случае поставленная задача ре-

шения не имеет.

В самом деле, изобразим на плоскости

([/,

V) все точки, коорди-

наты которых вычисляются по формулам

Обозначим полученное множество через

Из рис. 8 видно, что

наибольшее значение U

mSiX

)

и наибольшее значение V

(У

тах

)

до-

стигаются в разных точках, а точка с координатами

лежит вне множества

Cl.

Тем самым в исходной постановке задача, вообще говоря, нераз-

решима — удовлетворить обоим требованиями одновременно невоз-

можно. И следовательно, нужно искать какое-то компромиссное ре-

шение.

Среди известных стоит отметить два:

1) метод уступок

162

8.3. МЕТОД ИДЕАЛЬНОЙ ТОЧКИ. КОНКРЕТНЫЕ ПРИМЕРЫ

2) метод идеальной точки.

Оба метода используют множество Парето, составленное в дан-

ном случае из допустимых точек задачи, которые не могут быть

"сдвинуты" в пределах допустимого множества с улучшением сразу

по обоим критериям. Иными словами, улучшая значения одного из

критериев, мы неизбежно ухудшаем значения другого.

Метод (последовательных) уступок заключается в том, что ли-

цо, принимающее решение (ЛПР), работая в режиме диалога со спе-

циалистом, анализирует точки на границе Парето и в конце концов

соглашается остановиться на некоторой компромиссной.

Метод идеальной точки состоит в отыскании на границе Парето

точки, ближайшей к точке

утопии,

задаваемой ЛПР. Обычно ЛПР

формулирует цель в виде желаемых значений показателей, и часто

в качестве координат целевой точки выбирается сочетание наилуч-

ших значений всех критериев (обычно эта точка не реализуется при

заданных ограничениях, поэтому ее и называют точкой утопии).

8.3. Метод

идеальной

точки.

Конкретные примеры

Пусть на множестве

плоскости (х,у), определяемом системой не-

равенств

заданы две линейные функции:

Требуется найти решение задачи

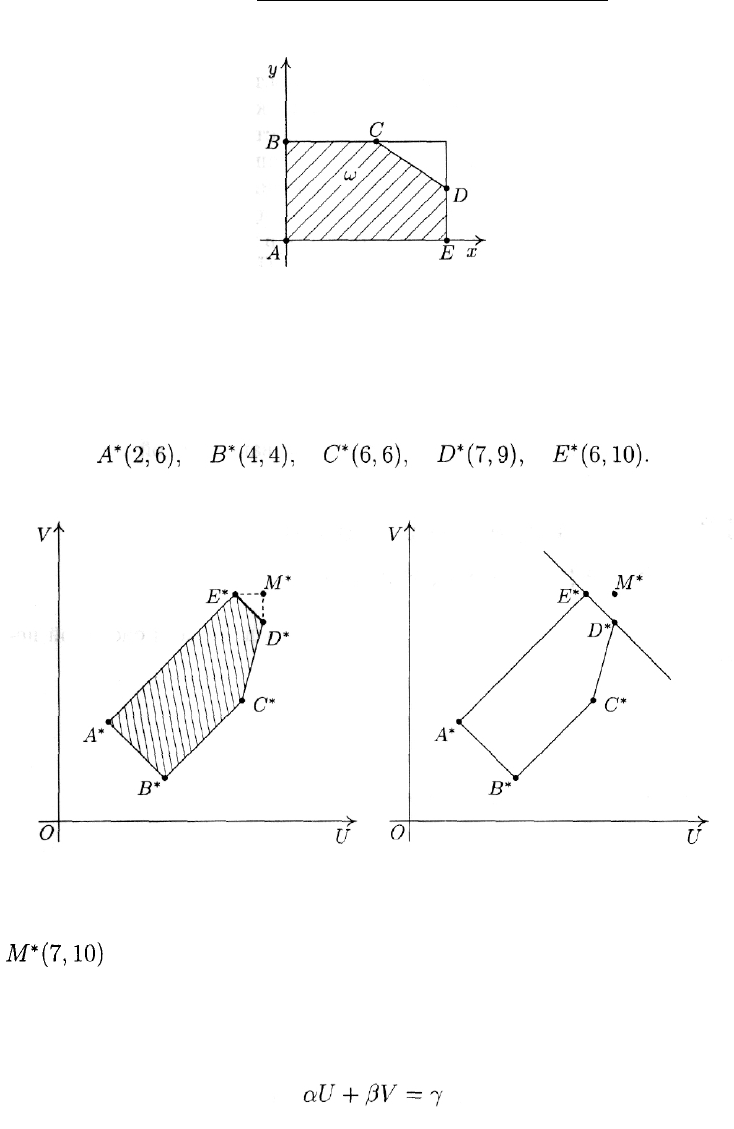
Множество со представляет собой пятиугольник (рис. 9), вершины

которого имеют следующие координаты:

163

ГЛАВА 8. МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ

Рис. 9

В силу линейности критериев U и V пятиугольник ABCDE пере-

ходит в пятиугольник A*B*C*D*E* (рис. 10), координаты вершин

которого вычисляются по формулам (1):

Рис. 10

Рис. 11

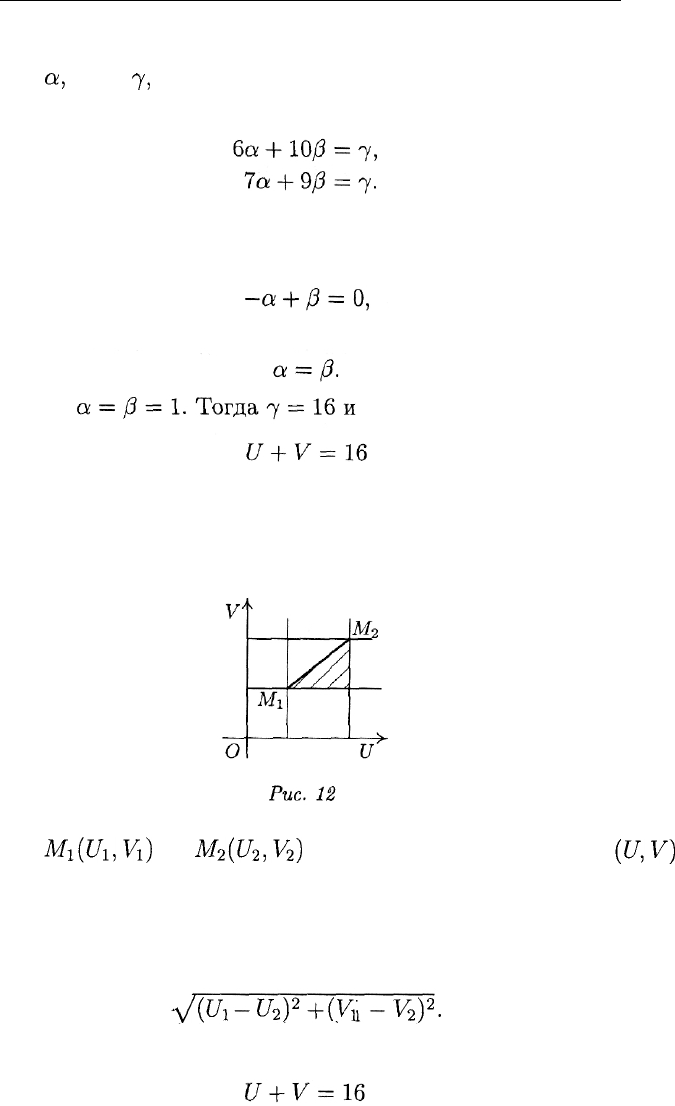
Находим границу Парето. Это отрезок D*E*. Точка утопии

М*(7,10)

считается заданной (ее координаты суть наибольшие зна-

чения U и V).

Требуется найти на множестве Парето точку, ближайшую к точке

утопии М*. Из рисунка видно, что искомая точка должна лежать на

отрезке D*E*. Проведем через точки D* и Е* прямую. Пусть

164

8.3. МЕТОД ИДЕАЛЬНОЙ ТОЧКИ. КОНКРЕТНЫЕ ПРИМЕРЫ

— ее уравнение (рис. 11). Чтобы отыскать конкретные значения па-

раметров

а,

(3 и

подставим в него координаты обеих точек — и

D*, и Е*. Получим

Вычитая из первого равенства второе, после простых преобразо-

ваний придем к соотношению

откуда

Положим

— искомое уравнение прямой.

Теперь стоит напомнить, как ищется расстояние между точками,

заданными своими координатами.

Пусть

Mi(Ui,Vi)

M2(U2,V2)

— точки на плоскости

(U,V)

(рис. 12). Для того чтобы найти расстояние между ними, достаточ-

но вычислить длину гипотенузы построенного прямоугольного тре-

угольника.

Воспользовавшись теоремой Пифагора, получим, что гипотенуза

равна

V(Ui

По условию задачи нам нужно определить на прямой

U + V= 16

165

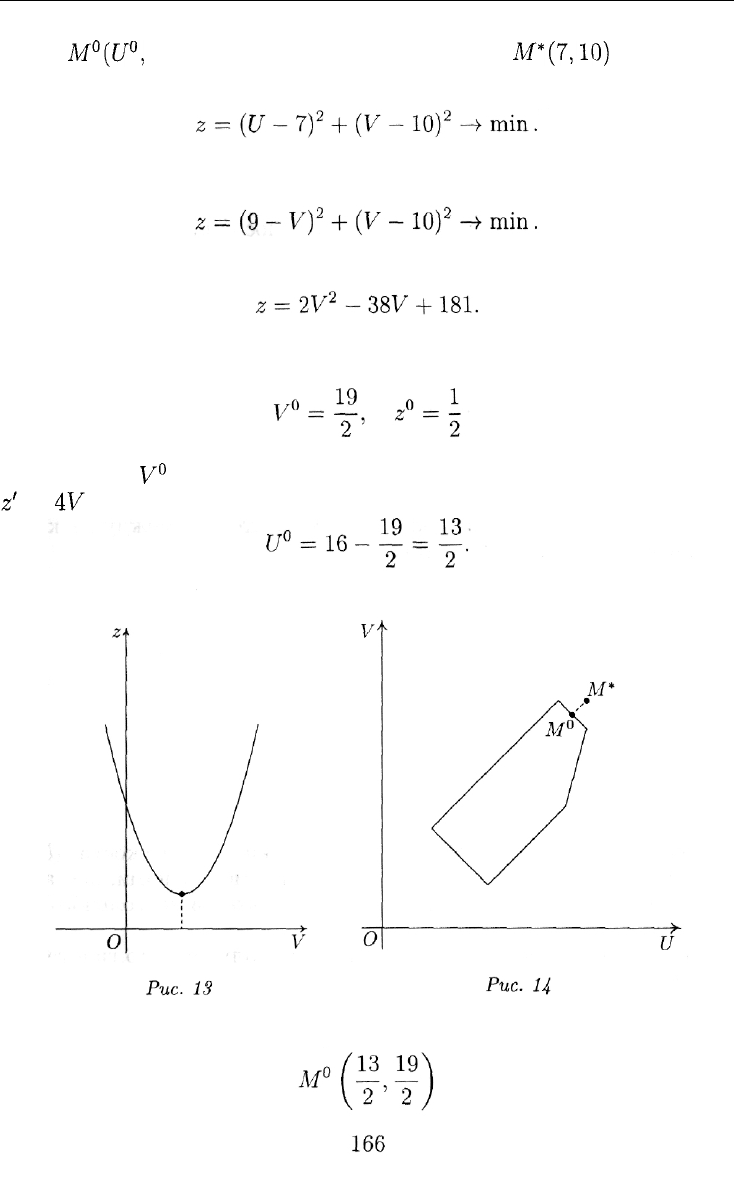
ГЛАВА 8. МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ

точку

М°([/°,

), расстояние которой от точки

М*(7,10)

минималь-

но, т. е. решить экстремальную задачу:

Так как U = 16 — V, то последнее соотношение можно переписать в

виде

Возводя в квадрат и приводя подобные, получаем, что

Это уравнение описывает параболу (рис. 13) с вершиной

(координата

го

находится из условия равенства нулю производной

4У

- 38). Тогда

Идеальная точка

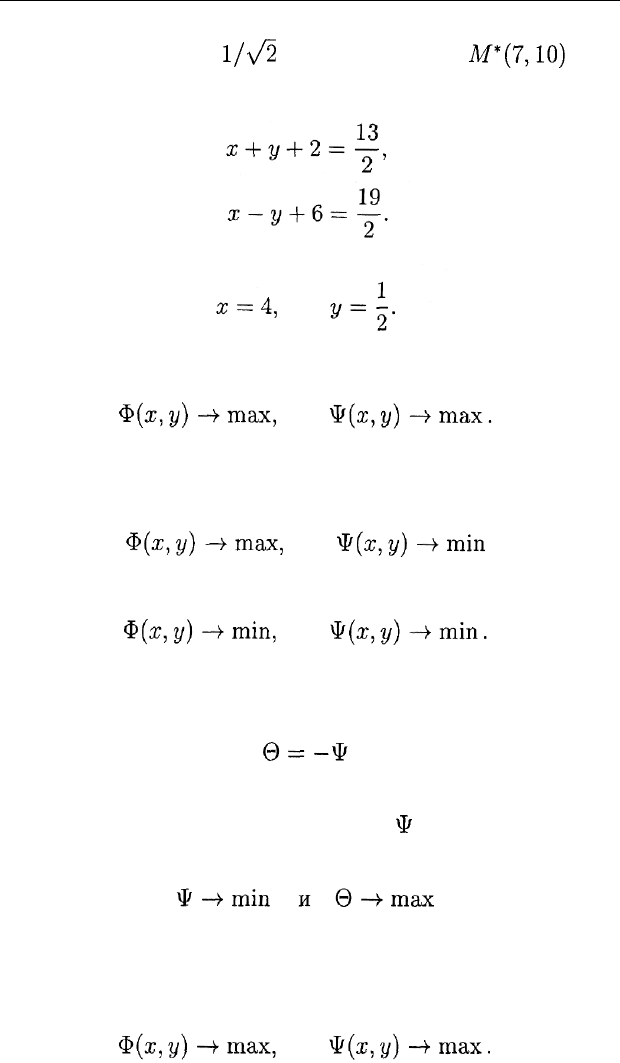
8.3. МЕТОД ИДЕАЛЬНОЙ ТОЧКИ. КОНКРЕТНЫЕ ПРИМЕРЫ

находится на расстоянии

1/\/2

от точки утопии

М*(7,10)

(рис. 14).

Соответствующие значения х и у легко находятся из системы линей-

ных уравнений

Имеем:

Замечание. Мы рассмотрели задачу, в которой

На практике часто встречаются случаи, когда требования выглядят

по-иному —

так:

или даже так:

Можно, конечно, решать такие задачи и непосредственно. Но зна-

чительно удобнее поступить по-другому, если учесть, что функция

обладает следующим свойством: она достигает наибольшего значе-

ния в точности в тех точках, где функция

принимает наименьшее

значение, и наоборот. Иными словами, условия

равносильны. Поэтому, поменяв в случае необходимости знак у кри-

терия на противоположный, мы можем свести любую двухкритери-

альную задачу к уже рассмотренной:

Рассмотрим соответствующий пример.

167

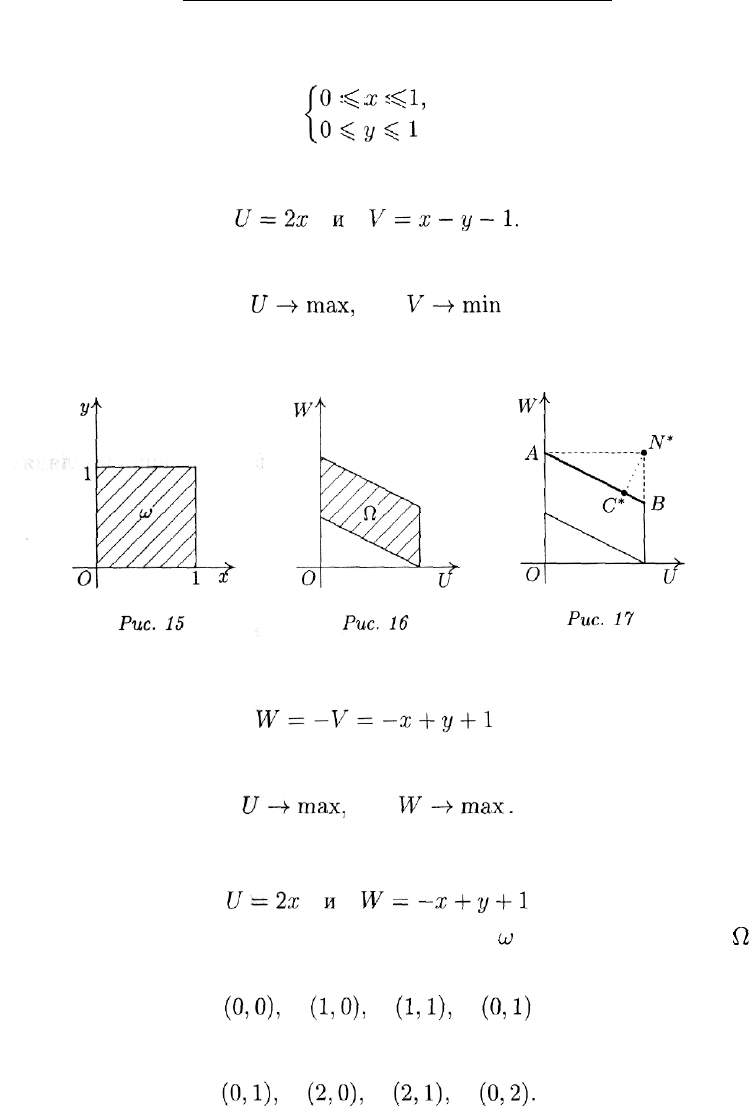
ГЛАВА 8. МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ

Пример 2. Пусть на множестве

ГО

(рис. 15) заданы две линейные функции:

Требуется найти решение задачи

при условии, что точка утопии М* имеет координаты (2, —2).

(2)

(3)

Введем новую функцию

Тогда требование (3) можно записать так:

Соответственно изменится и точка утопии — iV*(2,2).

Функции

линейны и преобразуют единичный квадрат

в параллелограмм

(рис. 16), при этом вершины квадрата

переходят в вершины параллелограмма

168

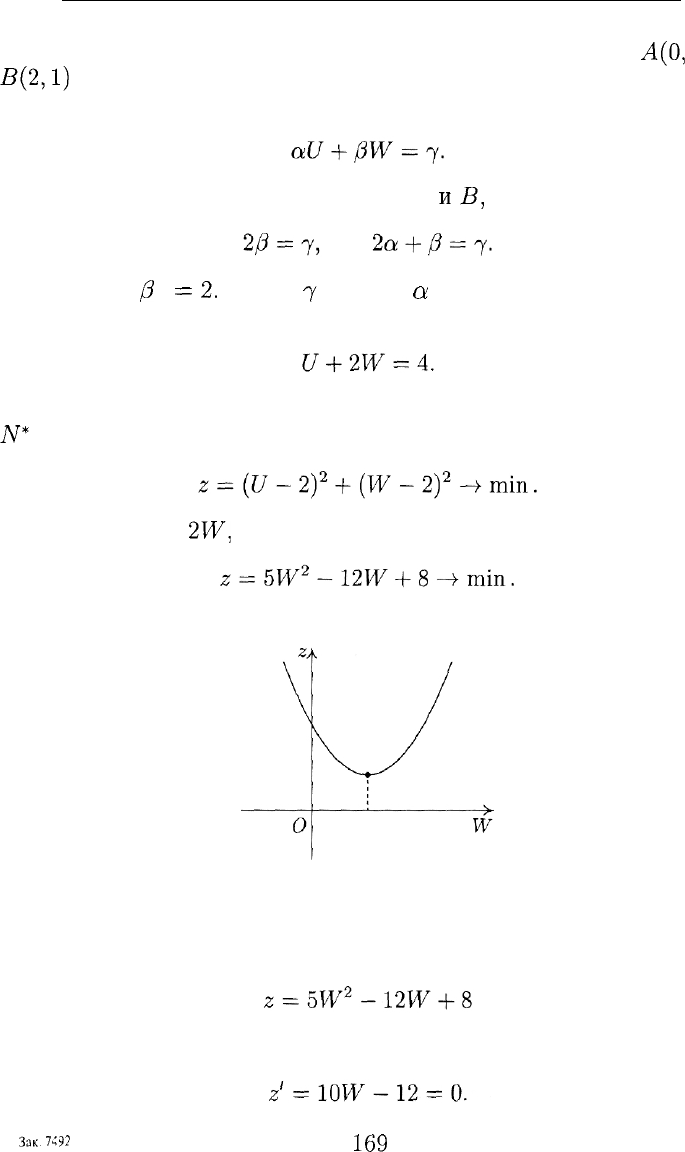
8.3. МЕТОД ИДЕАЛЬНОЙ ТОЧКИ. КОНКРЕТНЫЕ ПРИМЕРЫ

Множество Парето образуют точки отрезка с концами

А(0,

2) и

В(2,1)

(рис. 17). Проведем через эти точки прямую и найдем коэф-

фициенты ее уравнения

Подставляя в него координаты точек А

В,

получаем, что

Положим

Тогда

-у

— 4 и

= 1. Тем самым уравнение

искомой прямой имеет вид

Пусть C*(U,W) — точка этой прямой, ближайшая к точке

TV*

(2, 2). Это означает, что должно выполняться условие

Так как U = 4 —

2W,

то оно принимает следующий вид:

Рис. 18

Чтобы найти минимальное значение функции

(рис. 18), приравняем к нулю ее производную. Имеем:

12 3ак.74Э?

169

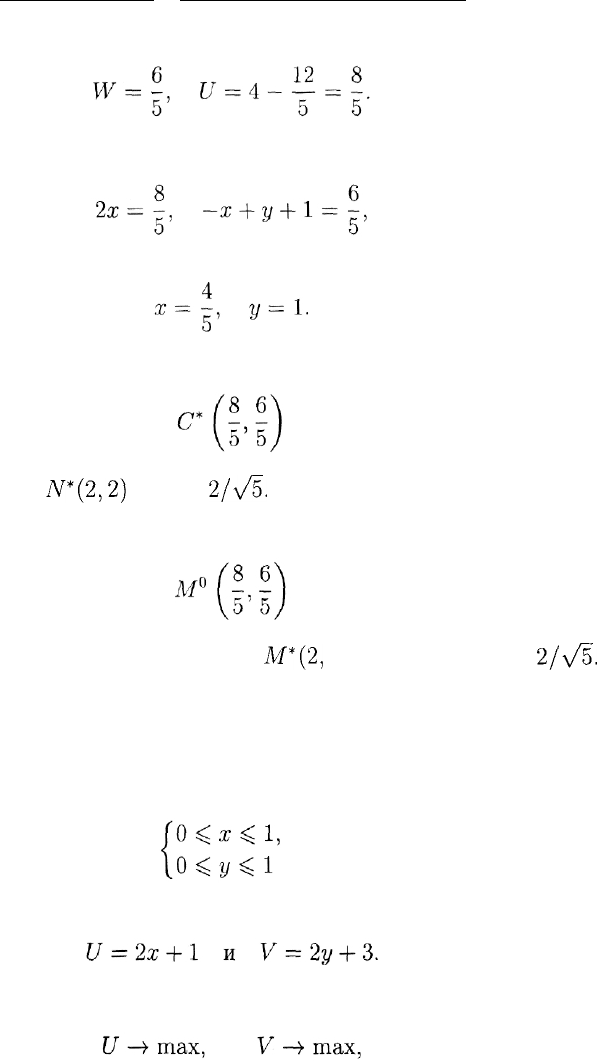
ГЛАВА 8. МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ

Отсюда

Соответствующие значения х и у находятся из уравнений (см. (2))

откуда

Расстояние от найденной точки

до точки утопии

*(2,2)

равно

2/л/5.

Ответ: идеальная точка

находится от заданной точки утопии

М*(2,

—2) на расстоянии

2/\/5.

8.4. Задания и ответы

1. На множестве

заданы две линейные функции:

Требуется найти решение задачи

при условии, что точка утопии М* имеет координаты (5,7).

170