Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

7.2. ОГРАНИЧЕНИЯ НА РЕСУРСЫ

и далее

Подобным же образом, умножая первое уравнение на

и складывая

со вторым, находим значение второй неизвестной. Имеем:

Отсюда

Таким образом, для того чтобы обеспечить прибавочный продукт

необходимо, чтобы столбец выпуска был равен

7.2. Ограничения на ресурсы

Модель Леонтьева отражает те потенциальные возможности, кото-

рые заложены в технологии производственного сектора. В этой мо-

дели предполагается, что все промежуточные продукты к тому мо-

менту, когда они оказываются необходимыми, уже произведены. Од-

нако в реальной ситуации нужно принимать в расчет наличие таких

ограничительных факторов производства, как мощность каждой от-

расли (материальные ресурсы) и общее количество рабочей силы в

системе (трудовые ресурсы).

Пусть L — общее число рабочих и

151

ГЛАВА 7. МОДЕЛЬ ЛЕОНТЬЕВА

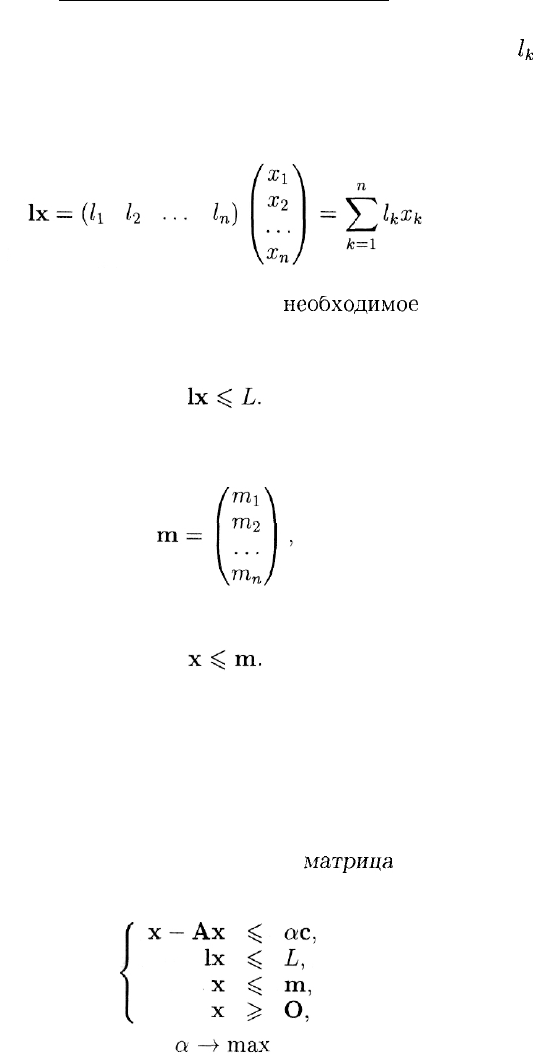
— матрица-строка затрат рабочей силы: каждый ее элемент

> О

показывает количество рабочих, необходимое для производства еди-

ницы k-ro продукта.

В предположении линейности производства произведение

показывает количество рабочей силы,

необходимое

в сфере произ-

водства при режиме работы х.

Ясно, что оно не может превосходить общего числа рабочих

Ограничения на мощности отраслей можно описать при помощи

столбца

превзойти который столоец выпуска не может,

При ограниченных ресурсах уже нельзя ставить вопрос об удо-

влетворении любого конечного спроса с > О. Тем не менее продук-

тивная система может обеспечить любую структуру прибавочного

продукта, т. е. соотношение между количеством прибавочных про-

дуктов первой и второй отраслей.

ТЕОРЕМА. Пусть дана продуктивная

лгатрица

А > О, столбцы

с > О и m > О, строка 1 > О и число L > 0. Тогда задача

•

имеет, и притом ровно одно, решение.

152

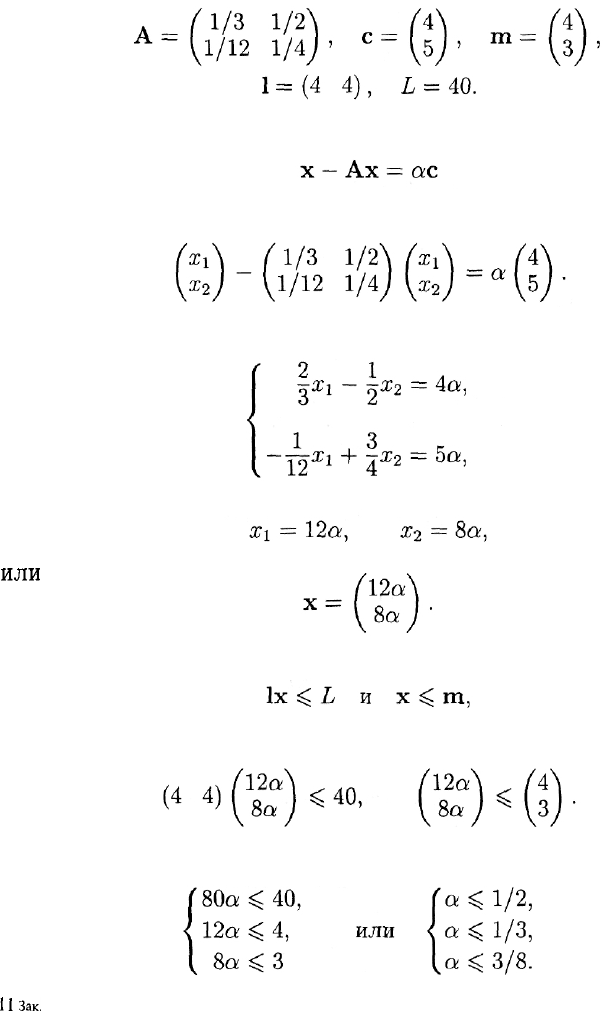
7.2. ОГРАНИЧЕНИЯ НА РЕСУРСЫ

Рассмотрим на конкретном примере, как можно решать такую

задачу.

Пример 3. Итак, даны

Начнем с решения системы

или подробнее:

Это можно записать в равносильной форме:

откуда

или

Полученный столбец должен подчиняться условиям

которые в данном случае принимают вид:

Отсюда имеем:

ПЗак.

7492

ГЛАВА 7. МОДЕЛЬ ЛЕОНТЬЕВА

Рис. 1

Наибольшее значение

а,

удовлетворяющее всем трем условиям,

равно 1/3 (рис. 1).

Ответ:

тах

= 1/3, столбец выпуска

конечный продукт

Замечание 1. Соотношение между количеством первого и количе-

ством второго прибавочного продукта

4:5

— то же, что и в случае

отсутствия каких-либо ограничений на материальные и трудовые

ресурсы.

Замечание 2. При п — 2 соотношения (1) принимают вид:

Решение системы уравнений можно записать так:

где

выражаются через элементы матрицы А и столбца с.

Отсюда получаем

154

7.3. ПРИБЫЛЬНЫЕ МАТРИЦЫ

или, исключая

а,

Полученное равенство на плоскости

(х^жг)

описывает прямую,

проходящую через начальную точку 0(0,0).

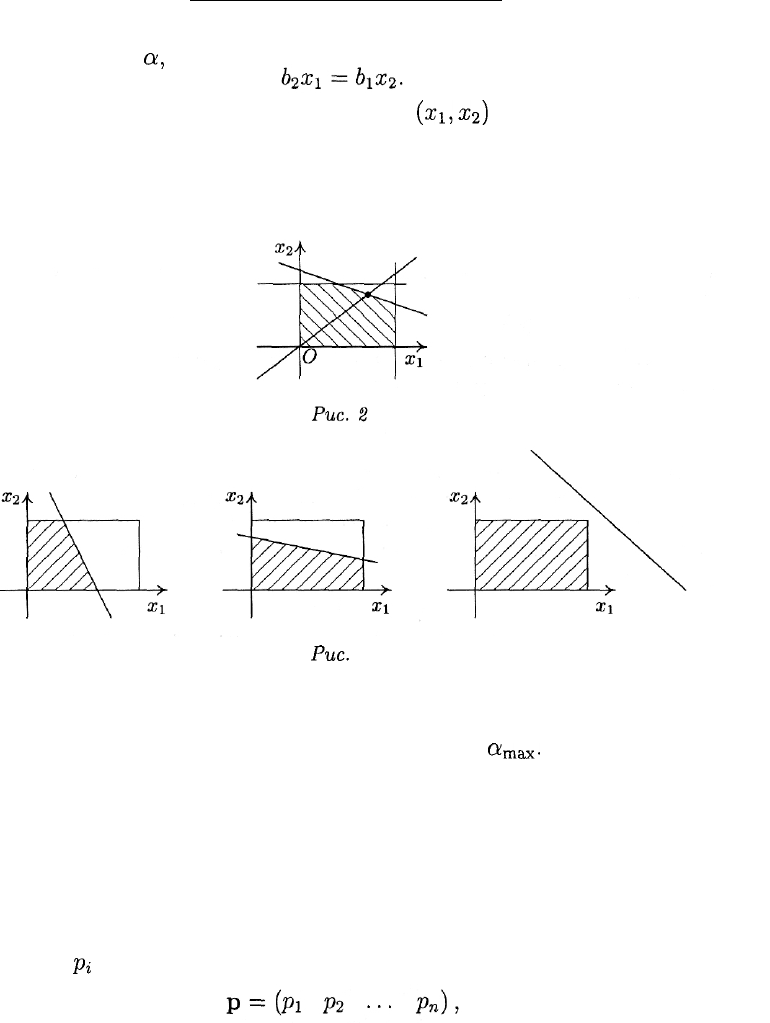
В свою очередь, неравенства (2) можно проиллюстрировать так,

как показано на рис. 2.

Рис.

На рис. 3 представлены все возможные случаи.

Замечание. На рис. 2 жирная точка отвечает

тах

7.3. Прибыльные матрицы

Предположим теперь, что отрасли закупают на внутреннем рынке

системы (друг у друга) продукты, которые необходимы им как сред-

ства производства.

Пусть

> О — цена единицы Г-ГО продукта. Строка

каждый элемент которой является ценой единицы соответствующе-

го продукта, производимого системой, называется строкой цен на

продукты или ценовой строкой.

155

ГЛАВА 7. МОДЕЛЬ ЛЕОНТЬЕВА

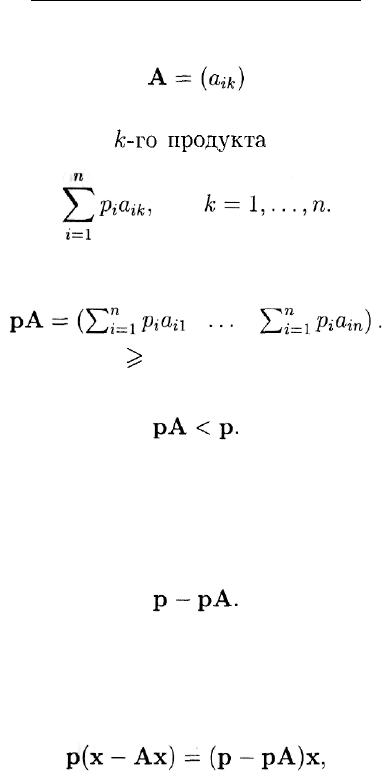
Пусть

— матрица материальных затрат системы. Тогда денежные издерж-

ки производства единицы

к-ro

продукта

будут равны

Из этих величин и складывается матрица-строка рА издержек про-

изводства:

Квадратная матрица А ^ О называется прибыльной, если суще-

ствует такая строка р > О, что

Это означает, что существует хотя бы одна система цен р, при

которой цена каждого продукта больше денежных издержек его про-

изводства и, следовательно, во всех отраслях обеспечивается поло-

жительная прибыль, выражаемая (в расчете на единицу продукции)

разностью

Ясно, что возможность получения прибыли неразрывно связа-

на с возможностью получения прибавочного продукта. Более того,

условия продуктивности и прибыльности матрицы (материальных

затрат) равносильны и всегда справедливо соотношение

означающее, что прибыль есть лишь денежное выражение прибавоч-

ного продукта, а прибавочный продукт есть материальное выраже-

ние прибыли.

7.4. Задания и ответы

Сфера производства некоторой экономической системы состоит из

двух отраслей. Найти оптимальный режим работы этих отраслей,

обеспечивающих структуру прибавочного продукта, заданного

столбцом с, при условии, что матрица материальных затрат А и

строка рабочей силы 1 имеют следующий вид:

156

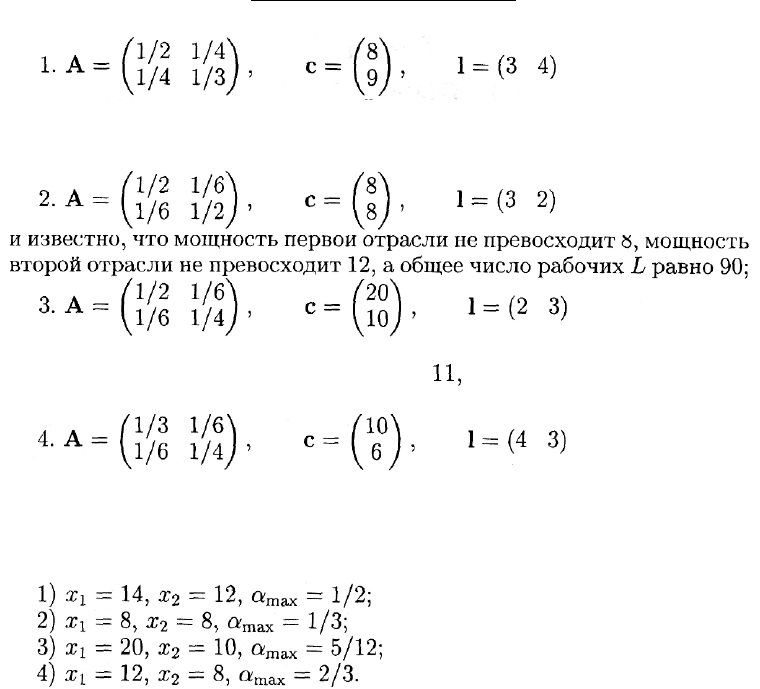
7.4. ЗАДАНИЯ И ОТВЕТЫ

и известно, что мощность первой отрасли не превосходит 24, мощ-

ность второй отрасли не превосходит 12, а общее число рабочих L

равно 120;

и известно, что мощность первой отрасли не превосходит 20, мощ-

ность второй отрасли не превосходит

11,

а общее число рабочих L

равно 72;

и известно, что мощность первой отрасли не превосходит 12, мощ-

ность второй отрасли не превосходит 8, а общее число рабочих L

равно 96.

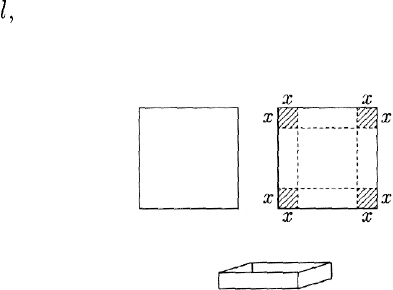
Ответы:

Глава 8

МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ

В рассматриваемой выше задаче линейного программирования мы

сталкивались с ситуацией, когда при известных условиях на чи-

словые параметры требовалось найти наибольшее (или наименьшее)

значение некоторой заданной целевой функции, которую часто на-

зывают также критерием. И тогда среди всех возможных наборов

неизвестных мы выбирали тот, который обеспечивал бы это иско-

мое экстремальное значение критерия. Однако при решении прак-

тических задач нередко приходится иметь дело с ситуациями, когда

необходимо одновременное выполнение нескольких условий (крите-

риев), зачастую противоречивых. Например, в стремлении приобре-

сти товар получше и подешевле покупатель сталкивается с тем, что

товар, вполне подходящий по цене, не удовлетворяет по качеству, а

высокое качество товара поднимает и цену.

Пример 1. Из железного листа, имеющего форму квадрата со

стороной

требуется скроить коробку максимально возможного

объема при минимальном расходе материала.

Рис. 1

158

8.1. МНОЖЕСТВО ПАРЕТО

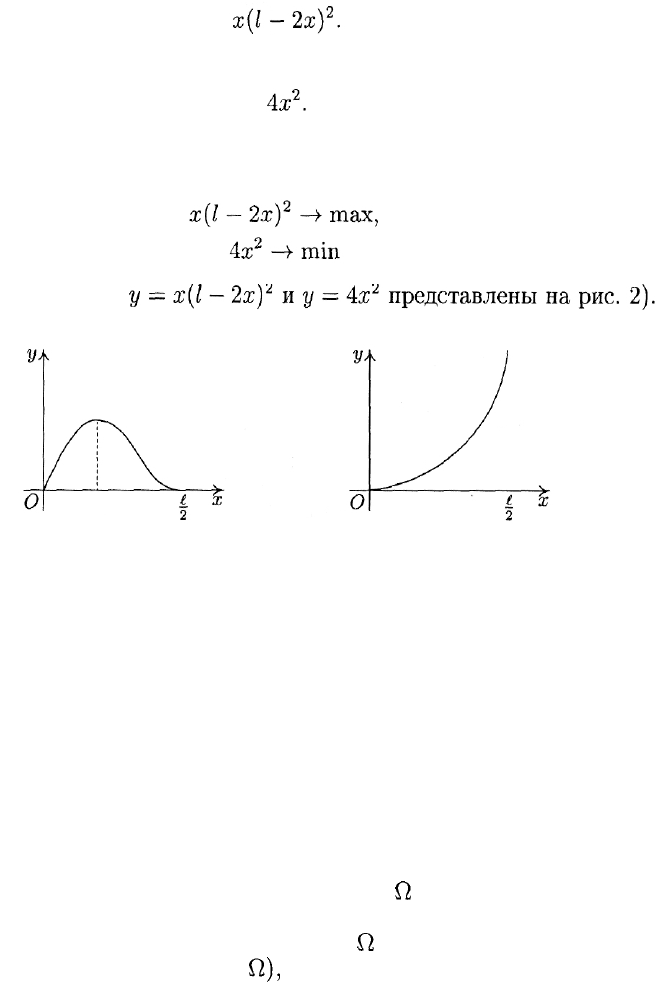
Вырезав из листа четыре квадрата с неизвестной пока стороной

х (рис. 1) и согнув по линиям, отмеченным пунктиром, мы получим

коробку, объем которой равен

При этом теряется железо общей площадью

По условию задачи требуется одновременное выполнение двух

условий (критериев):

(графики функций

Рис. 2

Ясно, что одновременно удовлетворить обоим критериям невоз-

можно: минимальные отходы получаются при х = 0 (не резать во-

обще), а максимального объема коробка достигает при х = (1/6)/.

В этой главе мы рассмотрим несколько задач с двумя критерия-

ми, считая их равноправными (вопроса о приоритетах мы коснемся

в другой главе).

8.1. Множество Парето

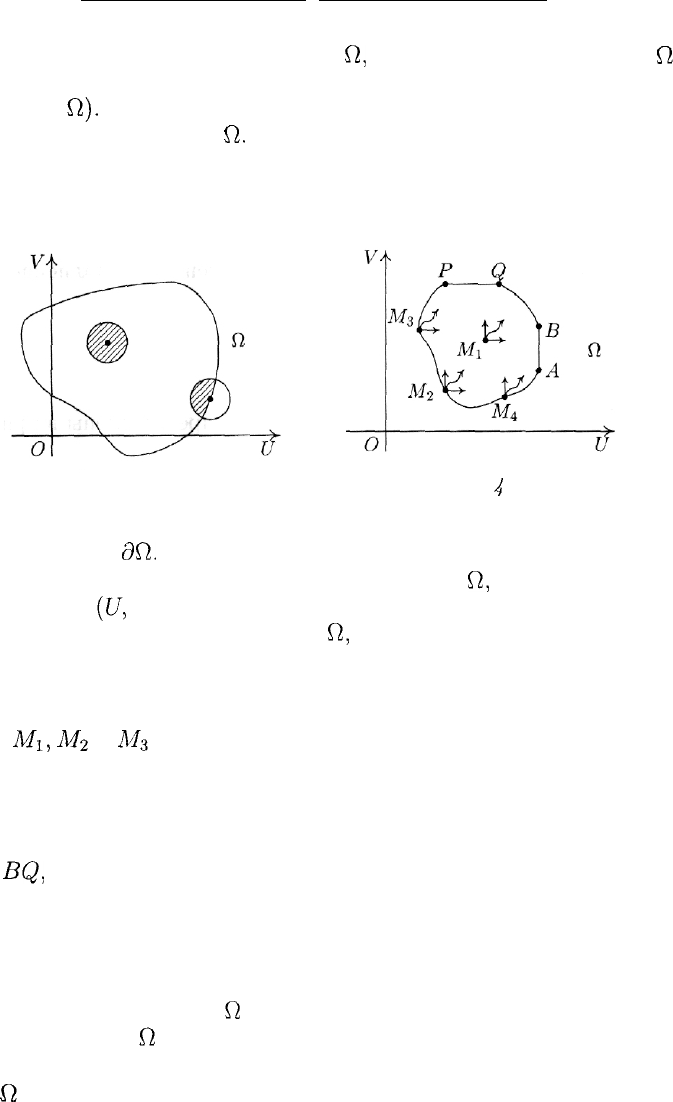
Рассмотрим на плоскости (U,V) множество

(рис. 3). Каждая его

точка обладает одним из следующих свойств: либо все точки, бли-

жайшие к ней, принадлежат множеству

Г2

(такая точка называется

внутренней точкой множества

Г2),

либо сколь угодно близко от нее

159

ГЛАВА 8. МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ

расположены как точки множества

так и точки, множеству

£1

не принадлежащие (такие точки называются граничными точками

множества

fi).

Граничная точка может как принадлежать, так и не

принадлежать множеству

В дальнейшем мы будем рассматривать

только такие множества, которым принадлежат все точки границы.

Множество всех граничных точек множества называется его грани-

цей.

Рис. 3

Рис. 4

Обозначение:

<ЭГ2.

Пусть М — произвольная точка множества

Г2,

внутренняя или

граничная, и

(U,

V) — ее координаты. Поставим следующий вопрос:

можно ли, оставаясь в множестве

П,

переместиться из точки М в

близкую точку так, чтобы при этом увеличились обе ее координа-

ты? Если М — внутренняя точка, то это, бесспорно, возможно. Если

же М — граничная точка, то такое возможно не всегда (рис. 4). Из

точек

Mi,

Мз

это сделать можно, но уже из точек вертикально-

го отрезка АВ можно переместиться, увеличивая лишь координату

V (координата U при этом остается неизменной). Перемещая точку

горизонтального отрезка PQ вправо, мы увеличиваем координату U

(при этом координата V сохраняет свое значение). Что же касается

дуги

BQ,

то перемещение вдоль нее способно лишь увеличить одну

из координат при одновременном уменьшении другой.

Тем самым точки множества fi можно разбить на три класса:

к первому классу относятся точки, которые можно сдвинуть так,

чтобы одновременно увеличились обе координаты и при этом точ-

ки остались в множестве

£1

(в этот класс попадают все внутренние

точки множества

и часть его граничных точек);

второй класс образуют точки, перемещением которых по множе-

ству

можно увеличить только одну из координат при сохранении

160