Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

4.1. ПРИМЕРЫ ЧИСЛОВЫХ ФУНКЦИЙ

Кубическая функция — это функция вида

где а,

Ь,

с и d — некоторые числа, причем а

0. Графиком кубиче-

ской функции является кубическая парабола (рис. 4).

Замечание. Пользователи графических редакторов (например, ре-

дактора Paint) для изображения различных кривых линий отмеча-

ют точки на экране, после чего компьютер сам проводит гладкую

кривую. Обычно эта кривая подбирается программой как раз среди

кубических парабол.

К простейшим элементарным функциям относится и функция

где к

0. Графиком этой функции является гипербола (рис. 5).

Рис.

111

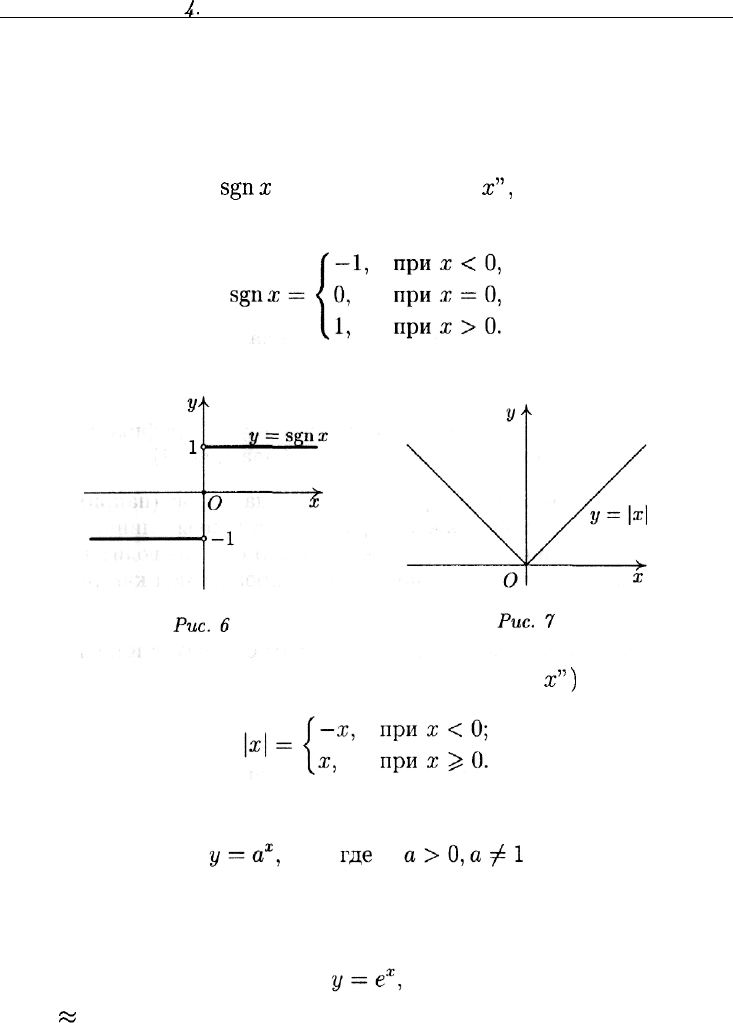
ГЛАВА

ФУНКЦИИ. ПРОИЗВОДНАЯ. ИНТЕГРАЛ

Замечание. Функции такого вида (с к > 0) — простейший способ

моделирования, например, зависимости спроса (у) от цены (х).

Функция может задаваться различным образом на отдельных

участках области определения. Простейшим примером может слу-

жить функция у —

sgnx

(читается "сигнум

х",

т. е. знак числа х),

определяемая следующим образом (рис. 6):

Еще один пример — функция у = \х\ ("модуль

х")

(рис. 7):

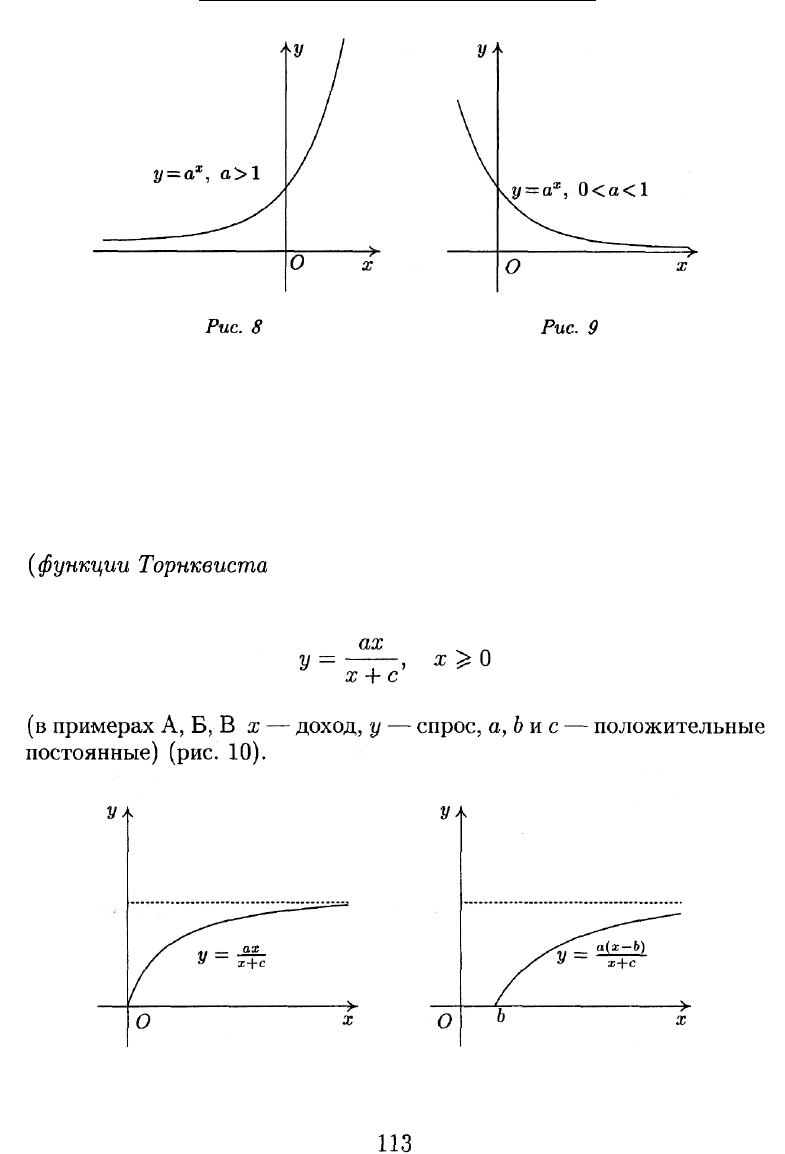
Показательная функция задается уравнением

(см. рис. 8, 9).

Среди показательных функций выделяют экспоненту — функ-

цию

где е

2,718.

Замечание. Быстро возрастающая показательная функция модели-

рует процессы типа роста народонаселения (у) с течением време-

ни (х).

112

4.1. ПРИМЕРЫ ЧИСЛОВЫХ ФУНКЦИЙ

Используемые в практических задачах функции зачастую имеют

и более сложный вид, однако их основные свойства можно проана-

лизировать и на простых примерах. В некоторых случаях простая

функциональная зависимость бывает весьма выразительной.

Приведем несколько примеров.

Функции спроса на товары в зависимости от доходов потребителя

{функции

Торнквиста

(Tornquist)) и их графики.

А. Спрос на товары первой необходимости:

Рис. 10

Рис. 11

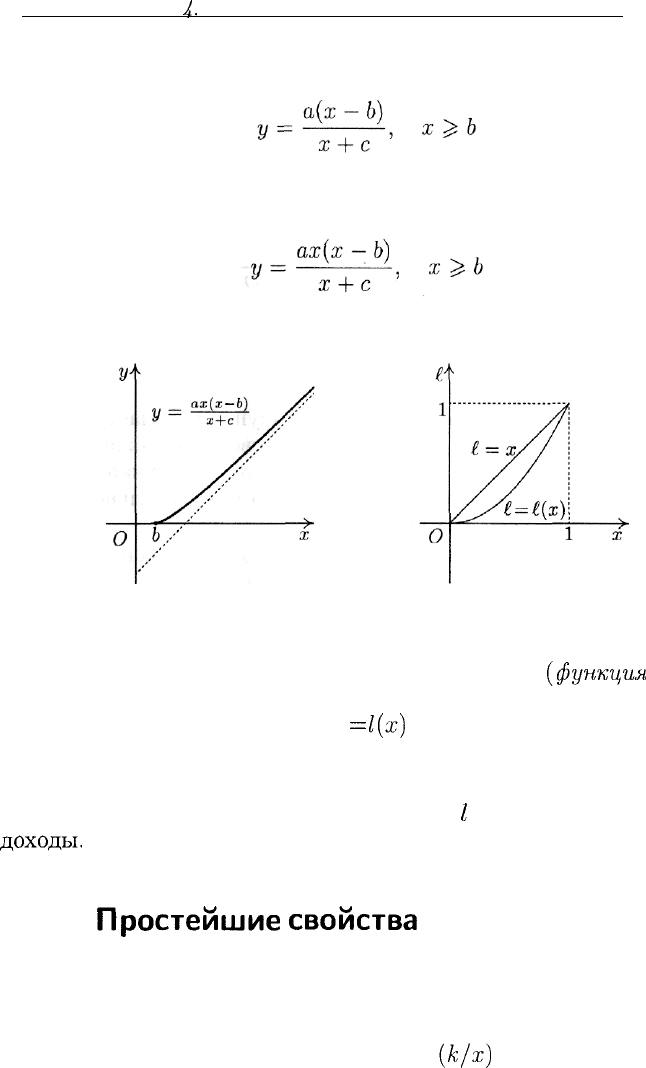
ГЛАВА

ФУНКЦИИ. ПРОИЗВОДНАЯ. ИНТЕГРАЛ

Б. Спрос на товары относительной роскоши:

(рис. 11).

В. Спрос на предметы роскоши:

(рис. 12).

Рис. 12

Рис. 13

Г. Функция распределения доходов в обществе

[функция

Лоренца

(Lorentz)):

1[х)

(примерный график изображен на рис. 13). Здесь х — доля населе-

ния с наименьшим доходом, / — доля дохода. Чем больше отклоня-

ется график функции Лоренца от прямой

= х, тем неравномернее

доходы.

4.2.

Простейшие

свойства

числовых функций

Важнейшим свойством функции является ее непрерывность. Гра-

фик непрерывной на отрезке функции можно начертить, не отрывая

ручки от листа бумаги. Линейная и квадратичная функции непре-

рывны на любом отрезке. Функции у =

(k/х)

и sgn x непрерывными

на отрезке, содержащем точку х — 0, не являются — в этой точке

обе функции разрывны.

114

4-2.

ПРОСТЕЙШИЕ СВОЙСТВА ЧИСЛОВЫХ ФУНКЦИЙ

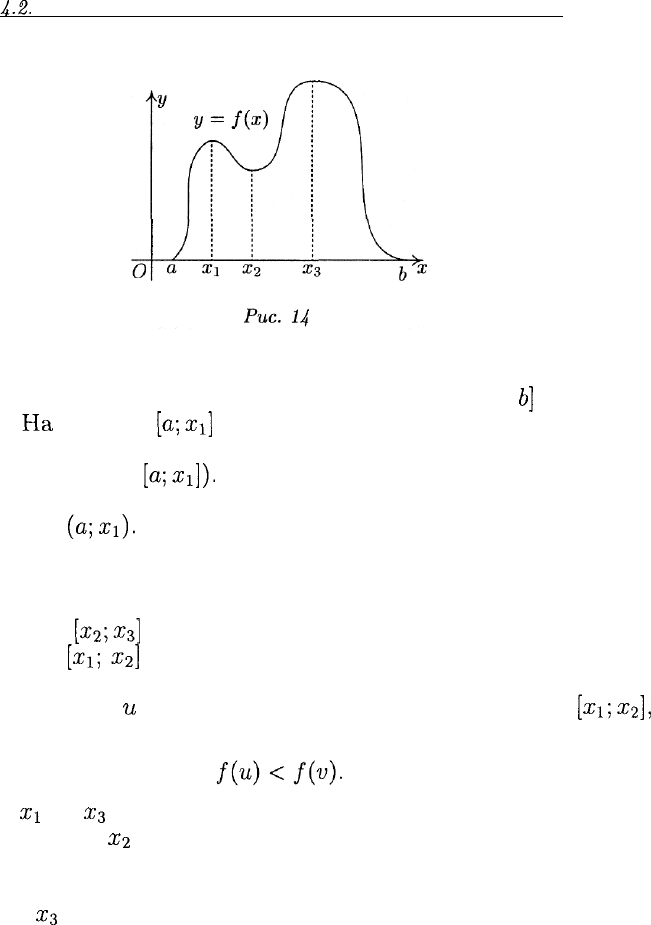
Для рассмотрения дальнейших свойств обратимся к рис. 14, на

котором изображен график непрерывной на отрезке [а;

Ь]

функции

у = f(x).

отрезке

[a;xi]

эта функция возрастает: чем больше

значение аргумента х, тем больше и значение функции f(x) (при х,

лежащем на отрезке

[o;xi]).

Можно сказать и так: функция f(x) возрастает в каждой точ-

ке интервала

(a;xi).

Это означает, что какую бы точку х из этого

интервала мы ни взяли, сдвинувшись от нее чуть-чуть вправо по

числовой оси, мы получим значения функции большие, чем f(x), a

сдвинувшись чуть-чуть влево, — меньшие, чем f(x).

На отрезке

[з^^з]

функция f(x) также возрастает.

На отрезке

[х\;

х^\

функция f(x) убывает — чем больше значение

аргумента, тем меньше значение функции. Говоря более строго: для

любых двух чисел

и v, и > v, принадлежащих отрезку

[ж^а^],

имеет место неравенство

Точки

х\

являются точками (локального) максимума фун-

кции f(x). Точка

— точка (локального) минимума функции f(x).

Точки локального максимума и локального минимума имеют общее

название — точки локального экстремума.

В точке

Хз

функция f(x) принимает свое наибольшее значение, в

точках а и b — наименьшее значение. Отметим следующий интуи-

тивно ясный факт:

непрерывная на отрезке функция может принимать максималь-

ное (минимальное) значение либо в точке локального максимума

(минимума), либо на границе отрезка.

Замечание. Понятие экстремального значения функции является

очень важным. Ведь при принятии того или иного решения мы за-

115

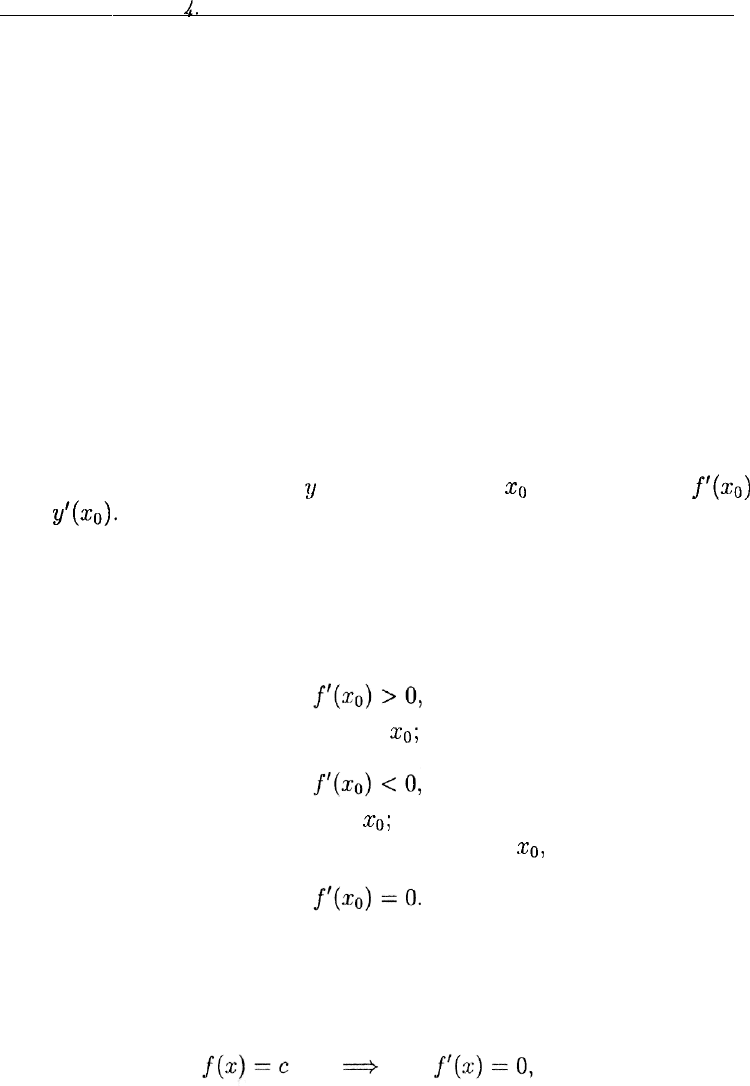
ГЛАВА

ФУНКЦИИ. ПРОИЗВОДНАЯ. ИНТЕГРАЛ

интересованы в том, чтобы оно было наилучшим. Переводя сказан-

ное на математический язык, мы стремимся найти точку, в которой

некоторая функция принимает экстремальное значение. Разумеет-

ся, в реальной (а не модельной) ситуации свести задачу принятия

решения к нахождению экстремума функции нелегко. Однако в не-

которых случаях это удается сделать. Поэтому очень важно уметь

находить экстремальные значения функций. С одним из основных

способов нахождения экстремума мы познакомимся ниже.

4.3. Производная и экстремум

Наряду с возрастанием (убыванием) функции можно учитывать ско-

рость этого возрастания (убывания). В одной точке эта скорость

больше, в другой — меньше. Скорость возрастания функции в точке

характеризуется числом, называемым производной функции в точ-

ке. Производная функции

= f(x) в точке

хц

обозначается

f'(x

)

или

у'(х

Операция нахождения производной называется диффе-

ренцированием.

Коротко говоря, производная — это скорость возрастания функ-

ции. Перечислим некоторые свойства производной в предположении,

что она существует.

Итак:

если

то функция f(x) возрастает в точке

Хо;

если

то функция f(x) убывает в точке

XQ\

если функция f(x) имеет экстремум в точке

хо,

то

Из последнего обстоятельства вытекает, что для нахождения экс-

тремума важно знать точки, где производная равна нулю.

Для вычисления производной полезны следующие правила.

1. Производная постоянной равна нулю:

где с — произвольное фиксированное число.

116

4.3. ПРОИЗВОДНАЯ И ЭКСТРЕМУМ

Производная в точке существует не всегда. Опишем три случая,

когда она не существует.

Первый случай — когда функция не определена в данной точке.

Например, функция у —

1/х

не имеет производной в точке

— 0.

Второй случай — когда функция определена, но разрывна в точ-

ке. Например, функция у =

sgnrc

не имеет производной в точке

= 0.

Наконец, третий случай — когда график имеет в точке излом.

Например, функция у = \х\ не имеет производной в точке

хо

= 0.

Опишем способ нахождения максимального и минимального зна-

чений непрерывной на отрезке функции. Эти значения могут до-

стигаться либо в точке, где производной не существует, либо в

точке, где производная равна нулю, либо на границе отрезка. При

исследовании функции f(x) на отрезке [а;

Ь]

надо решить уравнение

а также найти точки, где производной не существует. Значения

функции во всех этих точках и на границах отрезка включают в себя

и максимальное, и минимальное значения.

117

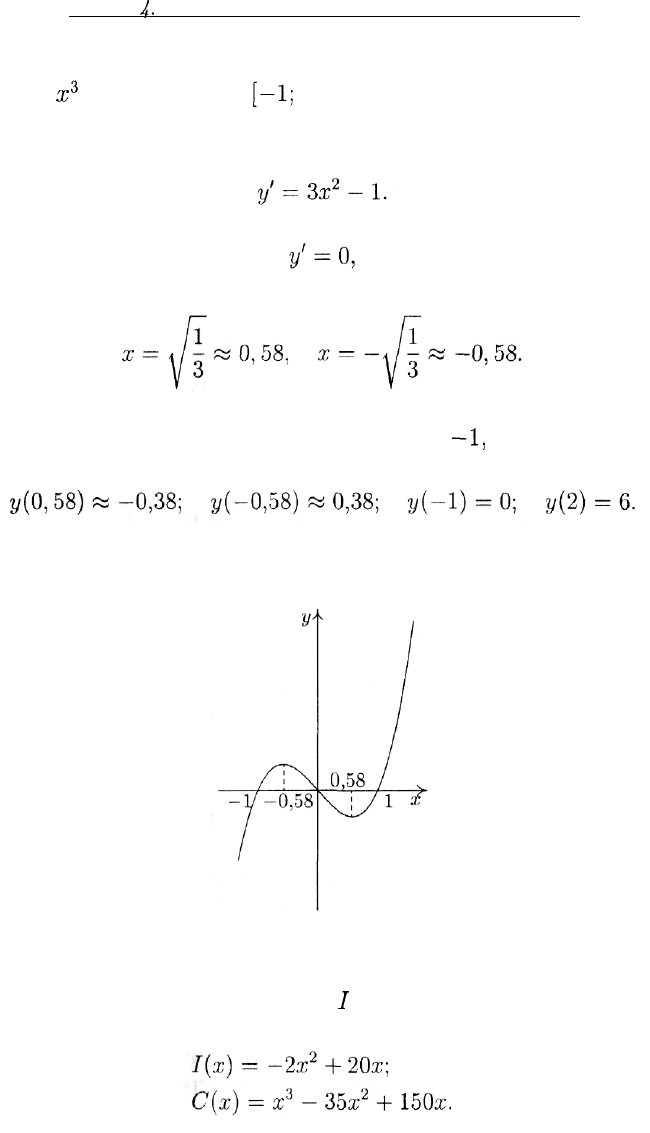
ГЛАВА

ФУНКЦИИ. ПРОИЗВОДНАЯ. ИНТЕГРАЛ

Пример 1. Найти максимальное и минимальное значения фун-

кции у =

— х на отрезке

[—1;

2].

Решение. Эта функция дифференцируема (т. е. имеет производную)

во всех точках. Найдем производную. Имеем:

Решая уравнение

получаем два корня:

Таким образом, экстремальные значения могут достигаться в одной

из четырех точек: х = 0,58, х = —0,58, х =

—1,

х — 2. Вычисляя

значения функции в этих точках, получаем

Таким образом, максимальное значение равно 6 (в точке х = 2),

минимальное равно —0,38 (в точке х — 0,58) (рис. 15).

Рис. 15

Пример 2. Зависимость дохода / и издержек С от объема про-

изводства х задается функциями следующего вида:

118

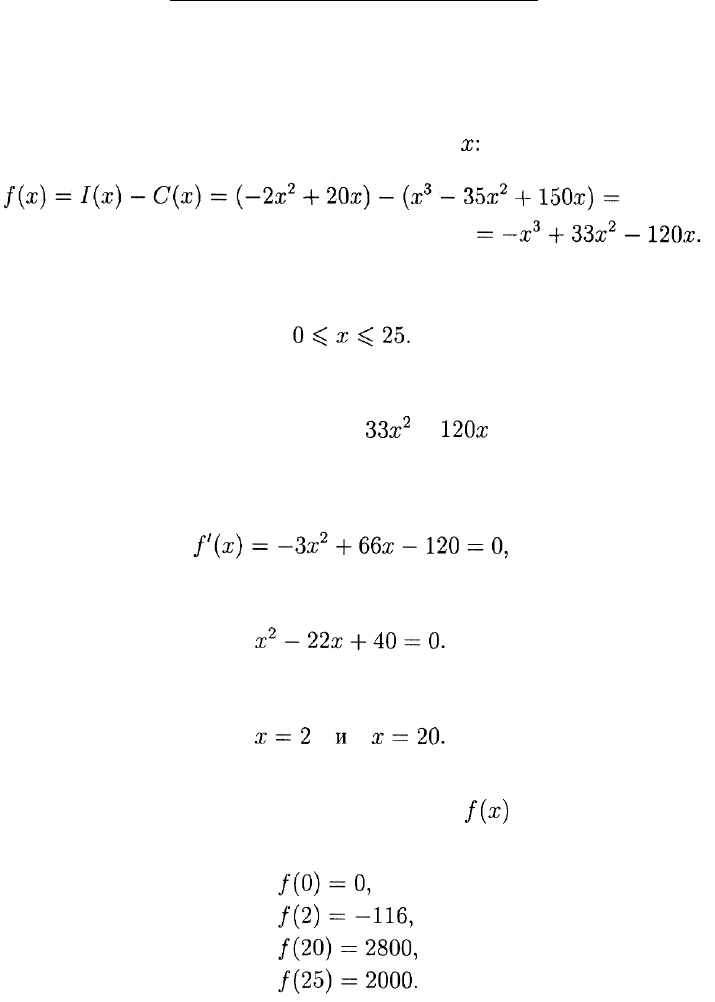
4.3. ПРОИЗВОДНАЯ И ЭКСТРЕМУМ

Производственные мощности позволяют производить до 25 единиц

продукции. При каком объеме производства прибыль максимальна?

Решение. Прибыль, равная разности дохода и издержек, задается

следующей функцией объема производства

х:

Производственные мощности диктуют следующее ограничение на

объем производства:

Таким образом, задача свелась к нахождению максимального зна-

чения функции

/(ж) = -х

ЗЗх

120х

на отрезке [0; 25].

Найдем производную и приравняем ее к нулю. Имеем

откуда получаем уравнение

Корнями этого квадратного уравнения являются числа

Оба этих значения принадлежат отрезку [0; 25]. Поэтому для нахо-

ждения максимального значения функции

f(x)

надо посчитать ее

значения в четырех точках. Нетрудно убедиться, что

Таким образом, прибыль максимальна (и равна 2800) при объеме

производства 20 единиц.

119

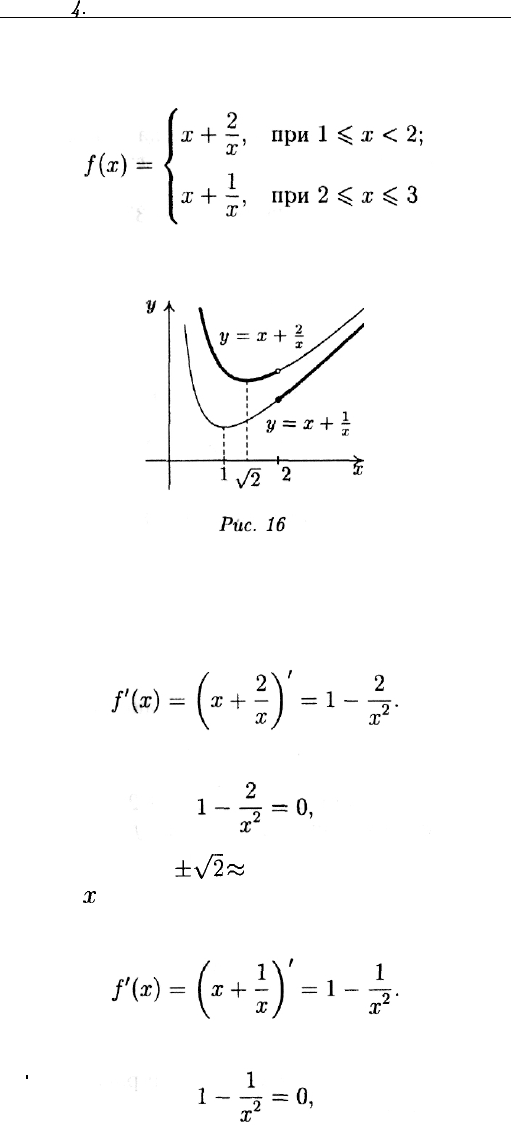
ГЛАВА

ФУНКЦИИ. ПРОИЗВОДНАЯ. ИНТЕГРАЛ

Пример 3. Найти максимальное и минимальное значения функ-

ции

на отрезке [1;3].

Найдем производную функции f(x) (ее график см. на рис. 16).

В точке х — 2 производной не существует (функция разрывна). На

интервале (1;2) имеем:

Решая уравнение

получаем два корня: х —

±л/2

±1,41. Интервалу (1;2) принадле-

жит лишь корень

= 1,41.

На интервале (2;3) имеем

Решая уравнение

•

120