Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

3.3. ЛИНЕЙНЫЕ СИСТЕМЫ

Рис. 35

Этот пример показывает, что к задачам целочисленного линей-

ного программирования следует подходить очень внимательно, а не

пользоваться "очевидным" рецептом и округлять нецелое решение

до ближайших целых значений.

Замечание. Зачастую описанную операцию разбиения исходной

задачи целочисленного программирования приходится повторять

несколько раз.

3.3.

Линейные

системы

Наши рассмотрения мы начнем с несколько условного примера.

Пример 12. У завода есть четыре потребителя, которым ежене-

дельно отгружается готовая продукция. Груз доставляется каждому

потребителю на автомашине упакованным в ящики, маркированные

в зависимости от вида продукции.

Однажды, когда автомашины были уже отправлены, но еще на-

ходились в пути, обнаружилось, что один из четырех видов груза

был отправлен по ошибке и его следует возвратить (причем в пол-

ной сохранности и без нарушения целостности остальных грузов).

Одновременно выяснилось также, что по недосмотру служащего не

осталось никаких сведений о том, как именно маркирована та пар-

тия ящиков, в которых находился этот подлежащий возврату груз.

А что же известно?

ГЛАВА 3. ЛИНЕЙНЫЕ ЗАДАЧИ

Известно количество маркированных ящиков каждого вида, об-

щий вес груза в каждой автомашине (см. таблицу),

а также и то, что ящики с возвращаемым грузом должны быть тя-

желее остальных.

Возникает вопрос: а нельзя ли дать рекомендации по изъятию

этого груза без распаковки и дополнительного взвешивания?

Оказывается, можно.

Приведем расчеты, при помощи которых совсем нетрудно выйти

из сложившейся чрезвычайной ситуации.

Обозначим через

х\.

вес ящика с

к-ы

видом груза. Тогда общий

вес груза на автомашине 1 можно подсчитать так:

что равно 51.

Проведем аналогичные подсчеты для трех других автомашин и

запишем результаты:

Таким образом, мы получили набор (систему) линейных уравне-

ний, в которые входят четыре неизвестные пока величины

, х

х^,

подлежащие определению. Покажем, как их можно найти

методом исключения неизвестной.

1-й шаг. Заметим, что если ко второму уравнению прибавить пер-

вое, умноженное на —2, то в результате получится соотношение

в котором неизвестной

х\

явно нет.

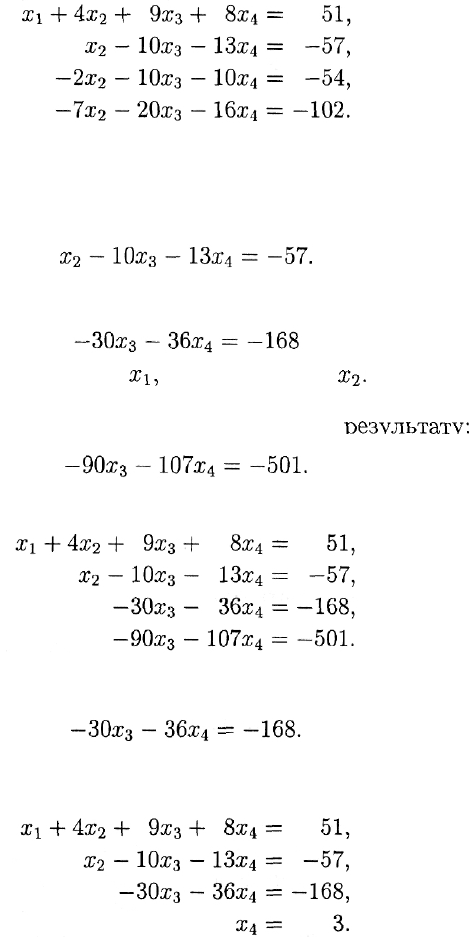
3.3. ЛИНЕЙНЫЕ СИСТЕМЫ

Поступая аналогичным образом с третьим (первое уравнение

нужно умножить на —2 и сложить с ним) и с четвертым (первое

уравнение нужно умножить на —3 и сложить с ним) уравнениями и

сохраняя неизменным первое, приходим к следующей системе соот-

ношений:

В дальнейших преобразованиях первое уравнение, активно работав-

шее на 1-м шаге, участия не принимает.

2-й шаг. На этом шаге рабочим является преобразованное второе

уравнение:

Умножим его на 2 и сложим с третьим уравнением. Полученное

соотношение

не содержит ни неизвестной

xi,

ни неизвестной

После сложения четвертого уравнения со вторым, предваритель-

но умноженным на 7, мы приходим к похожему

результату:

3-й шаг. На этом шаге рабочим является преобразованное третье

уравнение:

Прибавляя его к четвертому (предварительно умножив на —3),

окончательно получаем:

В итоге получаем систему уравнений следующего вида:

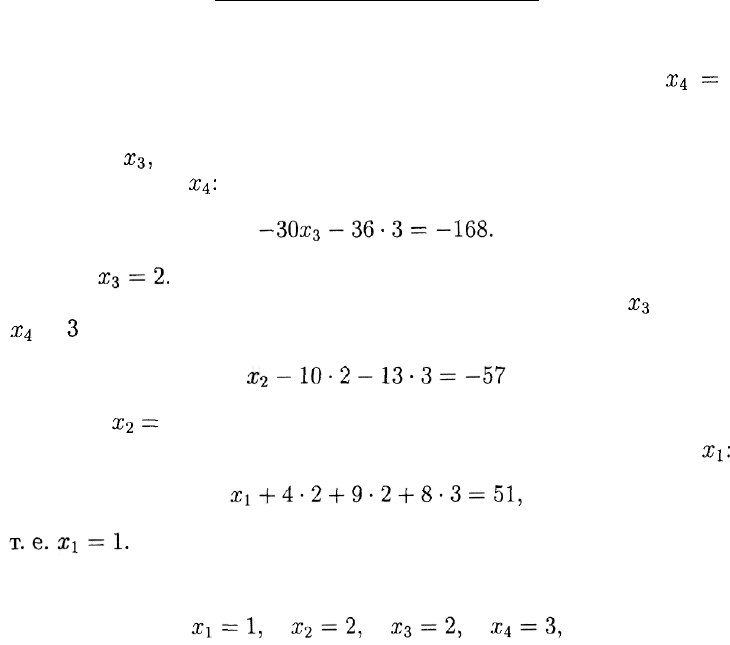
ГЛАВА 3. ЛИНЕЙНЫЕ ЗАДАЧИ

Завершающий этап. В результате проделанных преобразований

нам удалось найти значение одной из неизвестных, а именно

х±

Значения остальных неизвестных находятся совсем просто.

Сначала из третьего уравнения системы (8) находим значение не-

известной

предварительно подставив туда уже найденное значе-

ние неизвестной

х±.

Отсюда

Подставляя затем найденные значения неизвестных

х$

— 2 и

во второе уравнение системы (8), получаем:

и, далее,

Наконец, из первого уравнения находим значение неизвестной

Х\\

Запишем полученный ответ: из того, что

вытекает, что нужно вернуть на завод ящики с 4-м видом груза, т. е.

8 + 3 + 6 + 8 = 25 ящиков.

3.3.1. Что такое — матрица?

Читатель, видимо, уже успел заметить, что довольно часто либо при

начальном описании задачи, либо при более жестком ее формули-

ровании конкретный набор числовых данных удобно записывается

в виде прямоугольной таблицы. Подобные прямоугольные таблицы

естественно возникают при рассмотрении графов и сетей, при описа-

нии задач линейного программирования, при рассмотрении систем

линейных уравнений и еще во многих других случаях, где они ока-

зываются весьма кстати. Эти обстоятельства были замечены в сере-

дине XIX в., и появились матрицы. Сейчас вполне можно сказать,

что матрица является одним из основных математических понятий,

обладающим массой интересных и полезных свойств. Мы познако-

мимся лишь с некоторыми из них. Но сначала немного определений.

3.3. ЛИНЕЙНЫЕ СИСТЕМЫ

Матрицей А размера т х п называется набор т • п чисел

ац.

(г

1,2,

...,

т;

к —

1,2,

..., п) — элементов матрицы, записанных

в виде прямоугольной таблицы:

Набор

называется

г-й

строкой матрицы А, а набор

— к-м столбцом этой матрицы.

В случае когда т = п, матрица А называется квадратной, а число

п — ее порядком.

Пользуясь понятием матрицы, опишем для примера все три шага

преобразований, которые были проведены в примере 12.

Начнем с исходной системы уравнений и аккуратно выпишем все

коэффициенты. Имеем

Здесь строки матрицы соответствуют уравнениям системы, а столб-

цы — неизвестным. Последний столбец отделен от остальных вер-

тикальной чертой — этим подчеркивается его особое место в матри-

це (члены, расположенные в уравнениях по правую часть от знака

равенства, не содержат неизвестных величин (свободны от неизвест-

ных)).

Посмотрим теперь, как будут выглядеть матрицы, соответствую-

щие системам, получавшимся в конце каждого шага:

после 1-го шага:

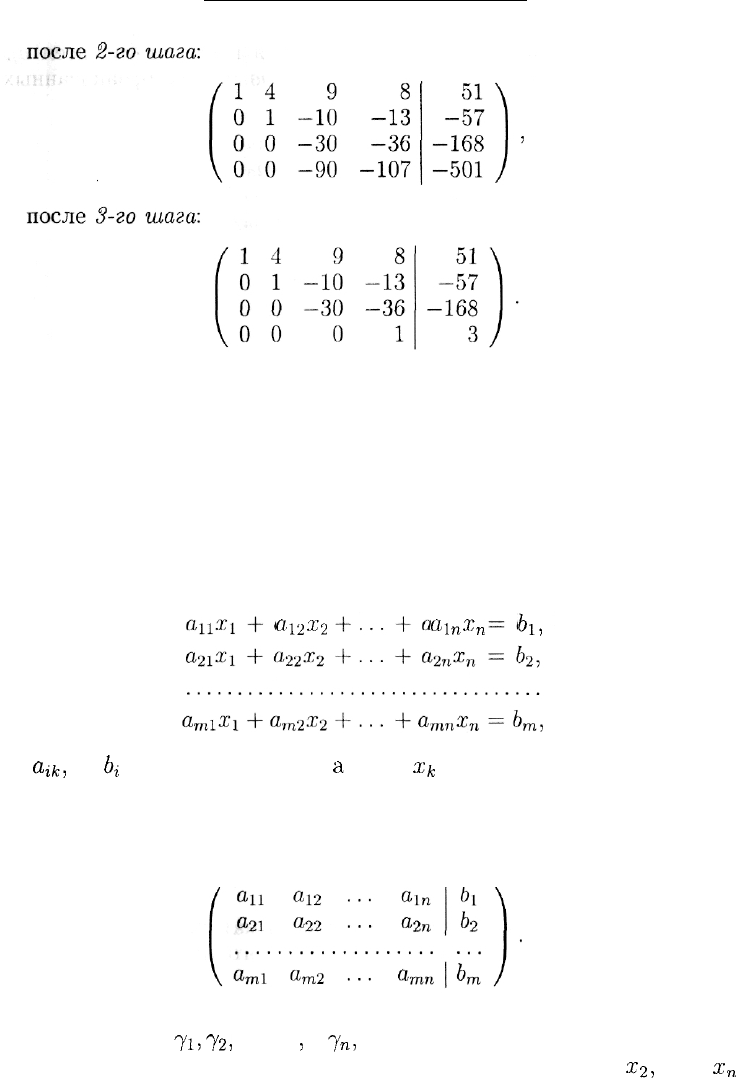
ГЛАВА 3. ЛИНЕЙНЫЕ ЗАДАЧИ

Замечание. Обратите внимание на то, как расположены нули в вы-

писанных матрицах.

3.3.2. Линейные системы общего вида

Довольно ясно, что и число линейных уравнений, и число связанных

ими неизвестных могут быть любыми.

Основные определения. Совокупность соотношений

Г2

+ ... +

(9)

где

CLik-,

— заданные числа,

числа

х^

рассматриваются как вели-

чины, подлежащие определению (неизвестные), называется систе-

мой т линейных уравнений с п неизвестными (линейной системой).

Заметим, что линейная система (9) полностью описывается мат-

рицей

Решением линейной системы (9) называется любой упорядочен-

ный набор чисел

7ь

Ъ,

• • •

•>

7п>

который при подстановке в каждое

уравнение системы (9) вместо набора неизвестных х\,

...,

обращает это уравнение в верное равенство.

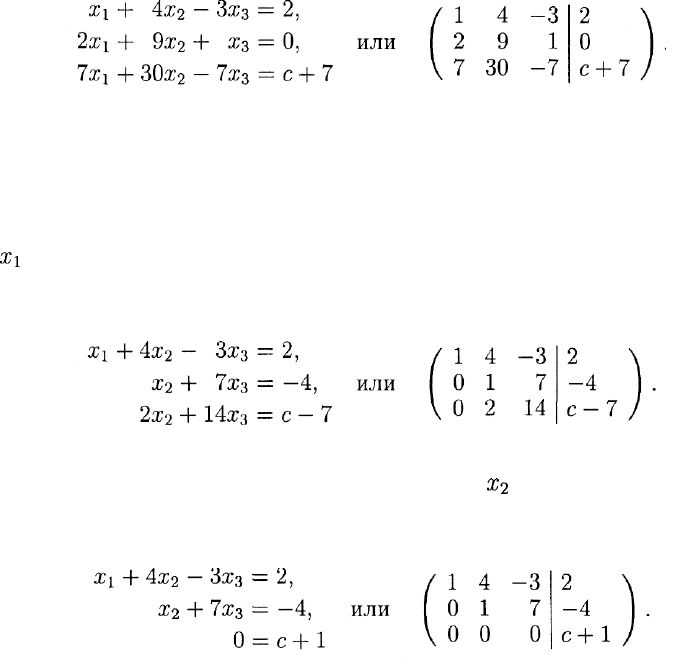
3.3. ЛИНЕЙНЫЕ СИСТЕМЫ

Замечание. Интересно отметить, что и в общем случае (как и для

системы двух уравнений с двумя неизвестными) при исследовании

системы могут встретиться только три варианта:

система имеет единственное решение,

система имеет бесчисленное множество решений,

система не имеет решений (такая система называется несовмест-

ной).

3.3.3. Исследование линейных систем

Метод последовательного исключения неизвестной, примененный в

ходе решения примера 12, универсален. Пользуясь этим методом,

можно исследовать любую систему уравнений и, если она имеет ре-

шение, найти его.

Пример 13. Дана система линейных уравнений

Требуется найти значения параметра с, при которых система:

1) несовместна,

2) совместна.

В случае, когда система совместна, отыскать ее решение.

1-й шаг. При помощи первого уравнения исключаем неизвестную

Х\

из второго и третьего уравнений (умножая первое уравнение на

—2 и —7 и соответственно складывая со вторым и третьим). В ре-

зультате получаем

2-й шаг. Сохраняя первое уравнение неизменным, при помощи

второго уравнения исключаем неизвестную

x-i

из третьего уравне-

ния (умножая второе уравнение на 2 и складывая с третьим). В

результате получаем

ГЛАВА 3. ЛИНЕЙНЫЕ ЗАДАЧИ

Заданная система

1) несовместна, если с + 1

О,

2) совместна, если с + 1 = 0.

При с = — 1 получаем

В итоге на три неизвестные величины

х\, х

имеем только

два условия.

Полагая

хз

= t, из второго уравнения находим, что

Отсюда

Подставим теперь полученные выражения в первое уравнение.

Имеем

Отсюда

Ответ:

1) при с

— 1 система несовместна,

2) при с = — 1 система совместна и

— ее решение (здесь t — любое число).

Замечание. С похожей ситуацией мы уже встречались в примере 10.

Соответствующая линейная система полностью описывается матри-

цей

3.4. ОПЕРАЦИИ НАД МАТРИЦАМИ

3.4. Операции над матрицами

Матрицы предоставляют весьма удобный способ записи количест-

венной информации и потому часто используются в самых разных

ситуациях.

Приведем лишь два примера.

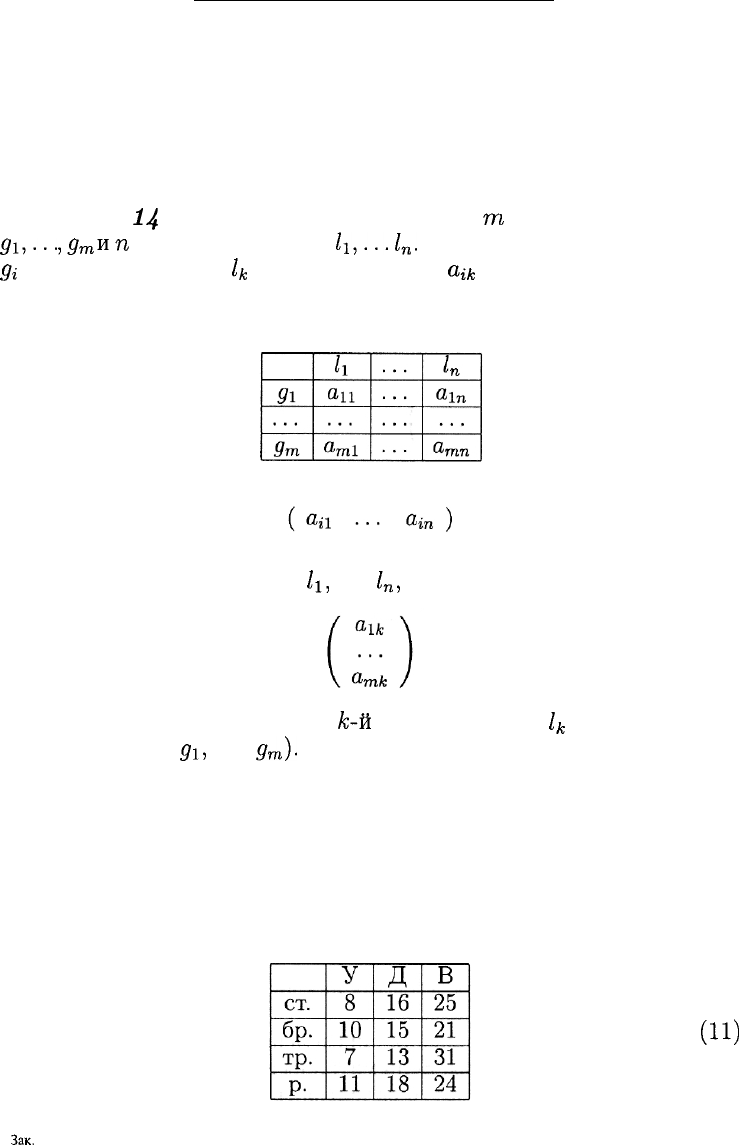
Пример

(расписание). В колледже

студенческих групп:

gi,...

,д

преподавателей:

,..., 1

Известно, что в г-й группе

к-й преподаватель

должен провести

а^

часов занятий. Таблица

(матрица) занятости студентов и преподавателей может быть запи-

сана в следующем виде:

(10)

(в г-й строке

указано количество часов занятий, которые г-я группа

каждым из преподавателей

li,

...,

а в к-м столбце

проведет с

— количество часов, которые

к-й

преподаватель

проведет с ка-

ждой из групп

...,

Пример 15. Мороженщица, торгующая в кинотеатре, перед

утренним сеансом продала 36 порций пломбира: 8 порций в стакан-

чиках, 10 порций в брикетах, 7 порций в трубочках и 11 порций в

рожках; перед дневным сеансом — 62 порции: соответственно 16, 15,

13 и 18. Наибольший спрос пришелся на вечер — 101 порция: 25,

21, 31 и 24 соответственно. Это можно записать компактно в виде

таблицы

(П)

Зак.

7492

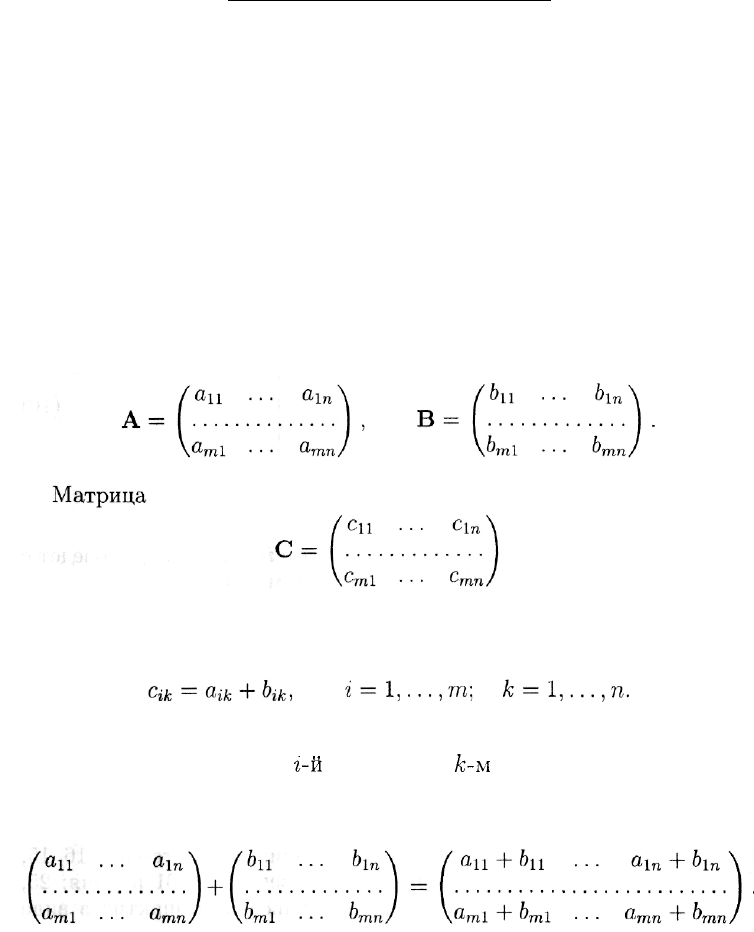
ГЛАВА 3. ЛИНЕЙНЫЕ ЗАДАЧИ

Нередко матрицы выступают не только в роли хранителей ин-

формации. Интересно, что с ними можно проводить различные опе-

рации, подобные тем, которые мы привычно совершаем с числами:

матрицы можно складывать, вычитать, умножать и пр. Однако дей-

ствовать здесь приходится осторожно, с оглядкой — не всякие ма-

трицы можно сложить, а с перемножением дело обстоит еще слож-

нее.

•

3.4.1. Сложение матриц

Пусть А и В — матрицы одинаковых размеров (т. е. состоящие из

одинакового числа строк и одинакового числа столбцов),

называется суммой матриц А и В, если ее элементы вычисляются

по правилу

Иными словами, складываются элементы матриц А и В, стоящие в

одинаковых позициях (в

г-й

строке и в

к-м

столбце), и полученная

сумма записывается в новой матрице С в ту же позицию (г, к).

Это можно записать и так:

Обозначение: А + В.

Вычитание матриц определяется аналогично.

Замечание. Операция сложения определена лишь для матриц, име-

ющих одинаковые размеры. Если матрицы имеют разное число строк

или разное число столбцов, то складывать их нельзя.