Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

3.1. КООРДИНАТЫ

В случае когда прямые заданы уравнениями общего вида

ГЛАВА 3. ЛИНЕЙНЫЕ

ЗАДАЧИ

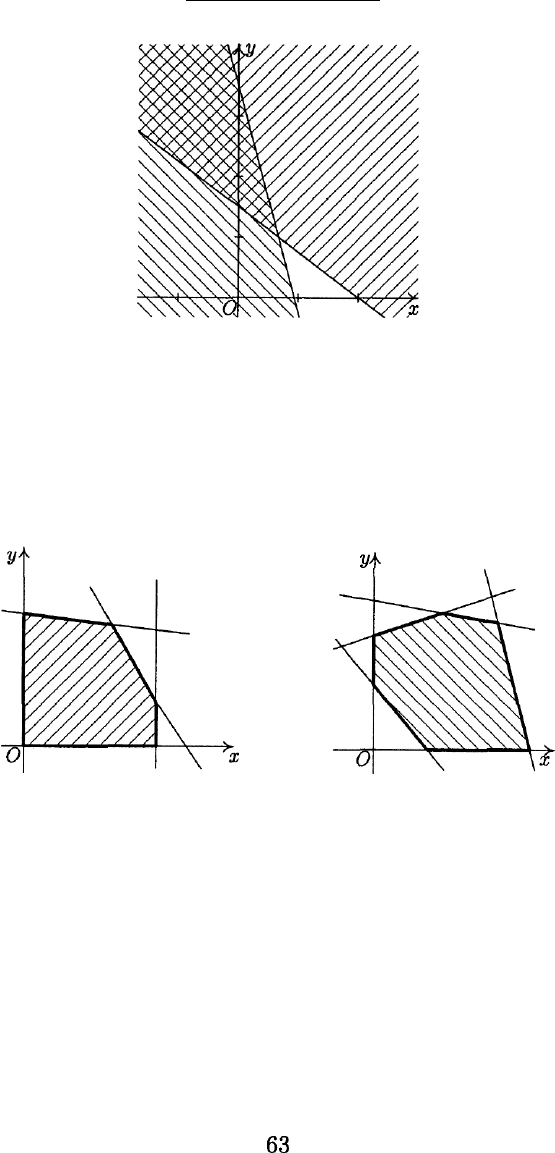
3.1. КООРДИНАТЫ

Рис. 20

Замечание. Можно рассматривать пересечение и большего числа по-

луплоскостей. При этом будут получаться и более сложные фигуры

(рис. 21). Однако все они наделены общим свойством — эти фигу-

ры являются выпуклыми.

УА-

Рис. 21

Выпуклость является естественным и хорошо известным матема-

тическим понятием. Даже весьма далекий от математики человек

имеет в целом правильное наглядное представление о том, что озна-

чают слова "быть выпуклым". Обратившись к такому человеку с

просьбой нарисовать что-нибудь выпуклое или распознать, является

предлагаемое изображение выпуклым или нет, можно быть уверен-

ным — это будет сделано без особого труда и верно.

Среди выпуклых фигур особое место занимают выпуклые много-

угольники. Некоторые из них хорошо известны — это треугольник,

прямоугольник, трапеция и т. д.

ГЛАВА 3. ЛИНЕЙНЫЕ ЗАДАЧИ

3.1.4. Экстремальное свойство плоских срезов

В заключение обратимся к линейным соотношениям, связывающим

три переменные величины.

Начнем с примера.

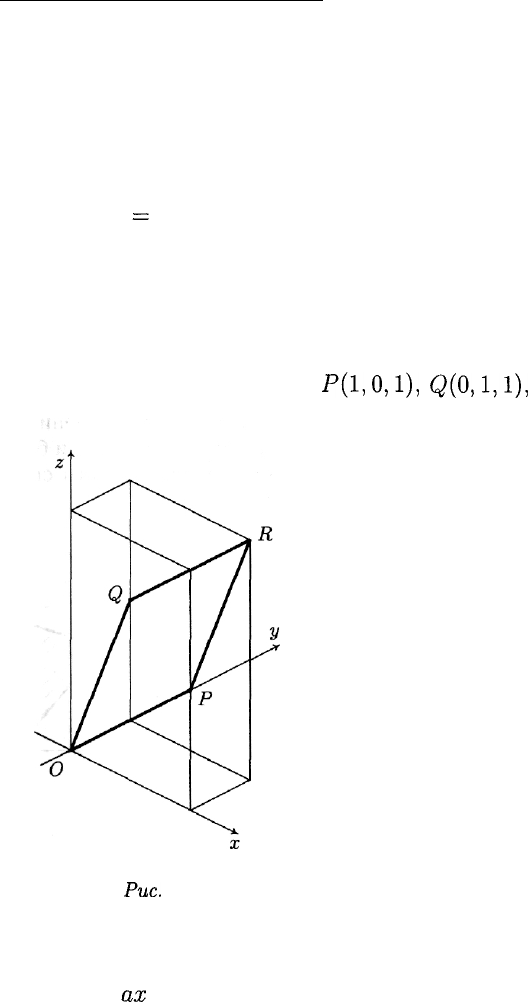
Пример 8. Формула

х + у

описывает хорошо известную операцию сложения: х и у — слага-

емые, a z — их сумма. Пусть в пространстве введена декартова

система координат Oxyz. Тогда множество точек, координаты х, у

и z которых связаны заданным равенством, является плоскостью.

На рис. 22 она показана как плоский срез прямоугольного парал-

лелепипеда, проходящий через точки 0(0,0,0),

Р(1,0,1),

0,(0,1,1),

•

Рис.

Приведенное соотношение, как и более общее

z =

ах

+ by + с,

является линейным. В пространстве с введенной координатной си-

стемой Oxyz такие линейные соотношения изображаются плоско-

стями.

3.2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

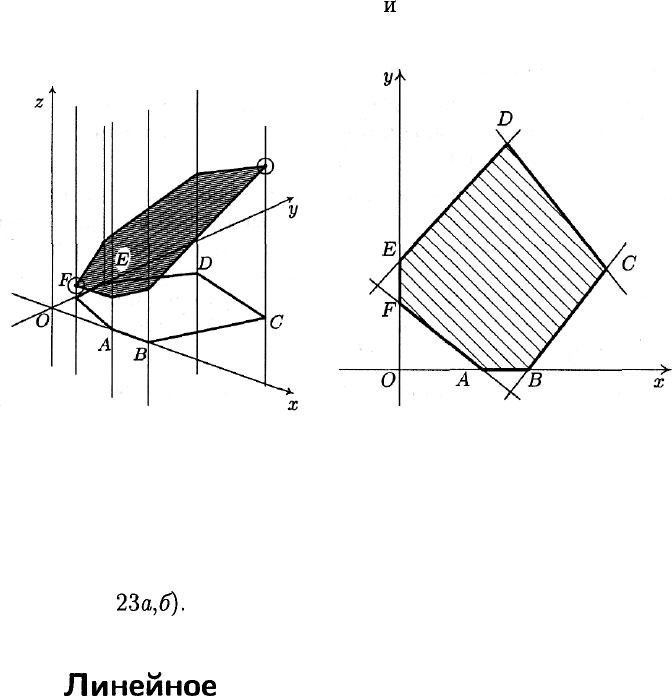
Важное замечание. Если внимательно рассмотреть плоский срез

на рис. 22, то нетрудно заметить, что

самая нижняя и самая верх-

няя его точки лежат на ребрах параллелепипеда.

Рис. 23

Оказывается, так будет всегда вне зависимости от того, как имен-

но проведен плоский срез призматической поверхности: самая ниж-

няя точка этого среза и самая верхняя его точка будут лежать на ее

ребрах (рис.

2За,б).

3.2.

Линейное

программирование

Изложенные положения лежат в основании так называемого графи-

ческого метода решения задач линейного программирования. Пока-

жем теперь, как их можно использовать для решения задач, совер-

шенно "негеометрических" по формулировке.

3.2.1. Задача о диете

Исторически задача о диете является одной из первых задач линей-

ного программирования.

Постановка задачи — первый и наиболее важный этап построе-

ния модели, способный обеспечить правильное решение проблемы.

ГЛАВА 3. ЛИНЕЙНЫЕ ЗАДАЧИ

Дама просто приятная решила похудеть и, как это нередко слу-

чается, обратилась за помощью к подруге.

Построение модели — рассмотрение этого этапа и является глав-

ной нашей целью в этом разделе.

Подруга — дама приятная во всех отношениях — посоветовала

ей перейти на рациональное питание, состоящее исключительно из

двух новомодных продуктов Р и Q.

Дневное питание этими новинками должно давать не более 14

единиц жира (чтобы похудеть), но и не менее 300 калорий (чтобы

не сойти с дистанции раньше). На банке с продуктом Р написано,

что в одном килограмме этого продукта содержится 15 единиц жира

и 150 калорий, а на банке с продуктом Q — 4 единицы жира и 200

калорий соответственно. При этом цена 1 кг продукта Р равна 15

руб., а 1 кг продукта Q — 25 руб.

Так как дама просто приятная в это время была весьма стесне-

на в средствах, то ее очень интересовал ответ на вопрос: в какой

пропорции нужно брать эти удивительные продукты Р и Q для то-

го, чтобы выдержать условия диеты и истратить как можно меньше

денег?

Переходим к переводу описанных обстоятельств на язык матема-

тических

символов.

Обозначим через х количество продукта Р и через у количество

продукта Q, требуемые для выполнения условий диеты.

Количество единиц жира, содержащегося в

кг продукта Р и в

у кг продукта Q, равно

15х

4у

и по условию диеты не должно

превосходить 14:

15а:

4у

14.

В свою очередь, количество калорий, содержащихся в

кг про-

дукта Р и в у кг продукта Q, равно

150ж

200у

и по условию диеты

должно быть не меньше 300:

150х

+ 200у

300.

Теперь о стоимости z продуктов. Она равна

z =

\Ъх

25у

и в соответствии с высказанными пожеланиями должна быть мини-

мальной.

3.2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

(2)

(3)

с которой теперь и нужно разобраться.

Для того чтобы применить графический метод, введем на плос-

кости координатную систему

Оху.

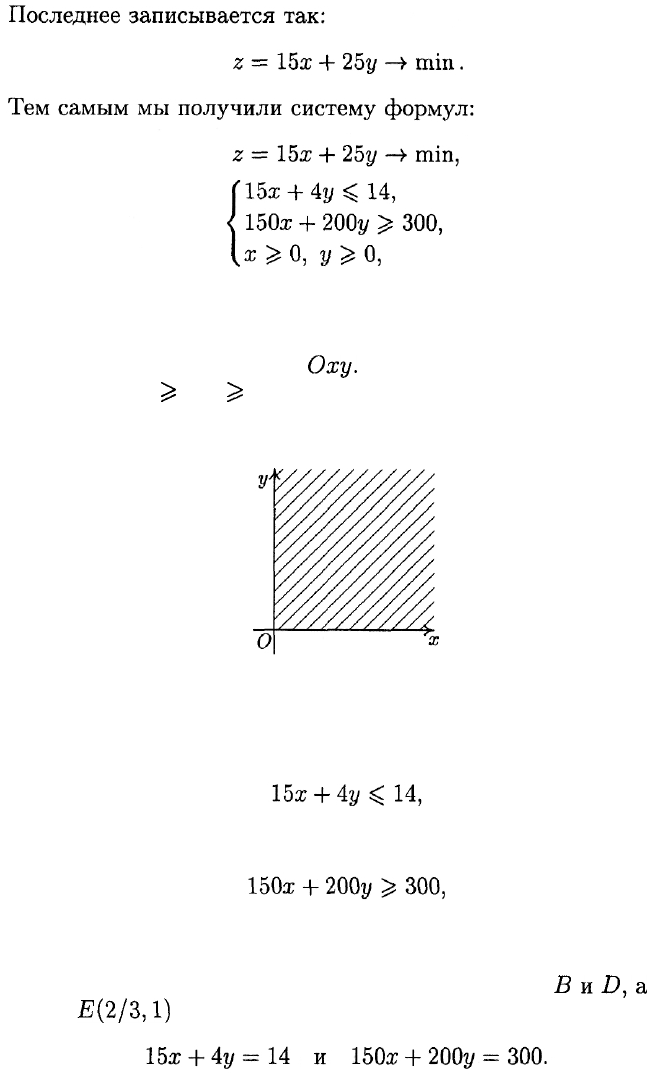
Из условий х ^ 0, у ^ 0 вытекает, что все, что нас может заинте-

ресовать, должно помещаться в первой четверти (рис. 24).

— на рис. 18.

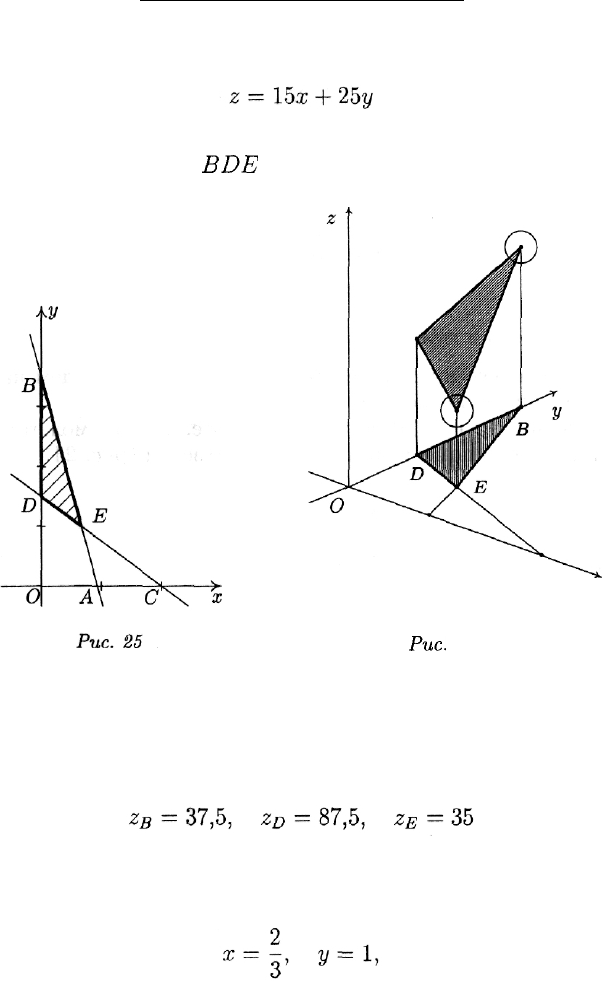
Сводя нарисованные картинки в одну, получим треугольник, изо-

браженный на рис. 25. Две его вершины суть точки

ВиДа

третья

вершина

£'(2/3,1)

является точкой пересечения прямых

Геометрический образ первого из неравенств,

показан на рис. 16, а второго,

ГЛАВА 3. ЛИНЕЙНЫЕ ЗАДАЧИ

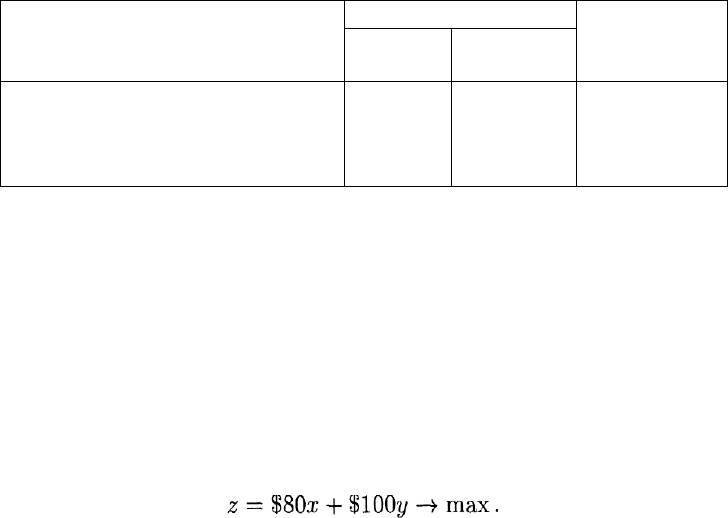
является плоскость. Нас интересует только та ее часть, которая ле-

жит над треугольником

BDE

(рис. 26). Соответствующий плоский

Рис.

и сравнивая полученные результаты, замечаем, что наименьшее зна-

чение (35) достигается в вершине Е.

Тем самым,

и искомая пропорция — 2:3.

Этап построения модели завершен.

Ответ на вопрос, волновавший даму просто приятную, получен:

для того, чтобы выдержать условия диеты и истратить как можно

срез обладает следующим важным свойством: как самая высокая,

так и самая низкая его точки располагаются непосредственно над

вершинами найденного треугольника.

Вычисляя значения z во всех трех вершинах этого треугольника:

Графиком линейной функции

3.2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

меньше денег, нужно брать рекомендованные продукты в отношении

два к трем.

Воспользовалась ли она этими рекомендациями, неизвестно.

Что же касается остальных этапов, как-то: проверка модели на

достоверность, применение модели (ни одну модель нельзя считать

успешно выстроенной, пока она не принята, не понята и не приме-

нена на практике) и (возможно) обновление модели, то мы оставим

их за рамками наших рассмотрений, так как основные трудности,

связанные с реализацией этих этапов, носят вовсе не математичес-

кий характер (и потому особенно сложны).

3.2.2. Задача о выпуске продукции

Фирма выпускает два вида древесно-стружечных плит — обычные

и улучшенные. При этом производятся две основные операции —

прессование и отделка. Требуется указать, какое количество плит

каждого типа можно изготовить в течение месяца так, чтобы обес-

печить максимальную прибыль при следующих ограничениях на ре-

сурсы (материал, время, затраты):

Затраты

Материал (фунты)

Время на прессование (часы)

Время на отделку (часы)

Средства (доллары)

Партия из 100 плит

обыч-

ных

улуч-

шенных

Имеющиеся

ресурсы

на месяд

4000

900

600

6000

если за каждые 100 обычных плит фирма получает прибыль, равную

80 долл., а за каждые 100 плит улучшенного вида — 100 долл.

Перейдем к построению математической модели поставленной за-

дачи.

Введем следующие обозначения. Пусть

х — количество партий в 100 плит обычного вида, изготавливае-

мых в течение месяца, а

у — то же для плит улучшенного качества.

Тогда ожидаемую прибыль можно записать так:

ГЛАВА 3. ЛИНЕЙНЫЕ ЗАДАЧИ

фунтов дерева. Ясно, что полученное число не может превосходить

количество материала, имеющегося в наличии, т. е. 4000 фунтов.

Тем самым, ограничения на материал имеют вид:

Подобным же образом рассчитываются ограничения на время из-

готовления и затраты:

Подведем итог: требуется найти такие значения х и у, подчинен-

ные условиям

'20ж

40у^

4000,

Ах + 6у

900,

Ах

600,

ЗОж

50у

6000,

•

для которых

Для того чтобы найти в первой четверти плоскости Оху множе-

ство точек, координаты (х, у) которых удовлетворяют указанным

выше неравенствам, необходимо сначала построить прямые (по точ-

кам их пересечения с координатными осями)

(4)

(5)

(6)

(7)

Для изготовления х партий в 100 плит обычного вида и у партий

в 100 плит улучшенного вида требуется