Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
Подождите немного. Документ загружается.

241
5.2.3. Íàéòè íàèáîëüøåå è íàèìåíüøåå çíà÷åíèÿ ôóíêöèè
z = 4x
2
+ y
2
16x 4y + 20
â çàìêíóòîé îáëàñòè D, çàäàííîé íåðàâåíñòâàìè:
x ≥ 0, x 2y ≤ 0, x + y 6 ≤ 0.
Ðåøåíèå.
à) Íàéäåì ÷àñòíûå ïðîèçâîäíûå è ïðèðàâíÿåì èõ ê íóëþ (íå-
îáõîäèìûå óñëîâèÿ ýêñòðåìóìà):
;2 ;042 ;0
;42)204164(
;2 ;0168 ;0
;168)204164(
0
22
0
22
==−=
∂
∂
−=
′
+−−+=
∂
∂
==−=
∂
∂
−=
′
+−−+=
∂
∂
yy
y
z
yyxyx
y
z
xx
x
z
xyxyx
x
z
y
x
Ñòàöèîíàðíàÿ òî÷êà x
0
= 2, y
0
= 2 ëåæèò â çàìêíóòîé îáëàñ-
òè, òàê êàê: 2 ≥ 0; 2 2 · 2 < 0; 2 + 2 6 < 0.
Íàéäåì âòîðûå ÷àñòíûå ïðîèçâîäíûå:
2)42(
;0)168( ;8)168(
2
2
2
2
2
=
′
−=
∂
∂
=
′
−=
∂∂
∂
=
′
−=
∂
∂
y
yx
y
y
z
x
y
x
z
x
x
z
è èõ çíà÷åíèÿ â ñòàöèîíàðíîé òî÷êå Ì (2; 2):
.2 ;0 ;8
2
22
2
2
=
∂
∂
==
∂∂
∂
==
∂
∂
=
ÌÌÌ
y
z
C
y
x
z
B
x
z
A
Òàê êàê ∆ = A · C B
2
= 8 · 2 0 = 16 > 0, òî â òî÷êå Ì
ôóíêöèÿ èìååò ýêñòðåìóì, à èìåííî ìèíèìóì, òàê êàê À = 8 > 0;
z
min
(2; 2) = 4 · 2
2
+ 2
2
16 · 2 4 · 2 + 20 = 0.
242
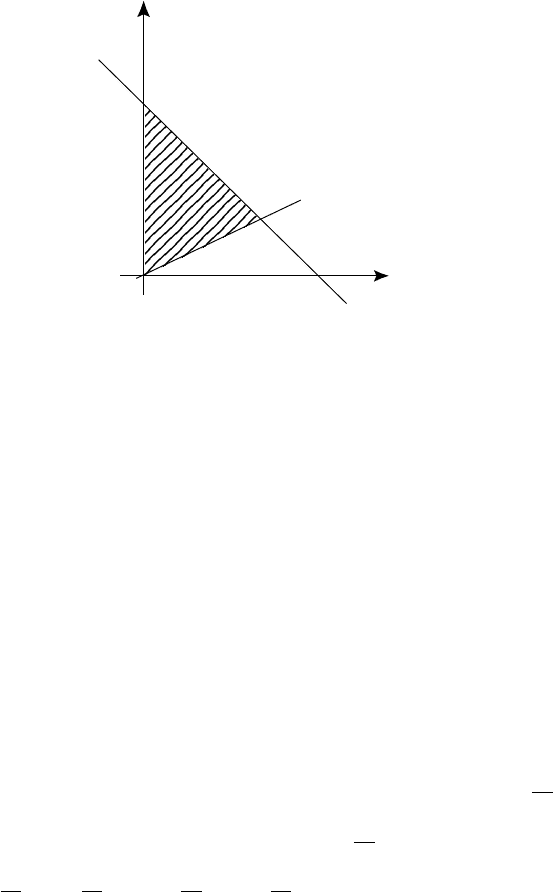
Ðèñ. 56
0
x
y
À
•
•
•
•
D
B
E
C
M
á) Ïîñòðîèì çàìêíóòóþ îáëàñòü ÎÀÂ (ðèñ. 56).
Ðàññìîòðèì êîíòóð õ = 0 (ïðÿìàÿ ÎÀ). Èìååì ôóíêöèþ îäíîé
ïåðåìåííîé: z = y
2
4y + 20. Èññëåäóåì åå íà ýêñòðåìóì:
z′ = 2y 4.
Èç z′ = 0 èìååì 2y 4 = 0 èëè y = 2. È òàê êàê
,02)2()42()2(
22
>==
′
−=
′′
==
yy
y
z
òî èìååì ìèíèìóì è z
C
= z (2) = 2
2
4 · 2 + 20 = 16.
Äàëåå ðàññìîòðèì êîíòóð õ + y 6 = 0 èëè y = 6 õ (ïðÿ-
ìàÿ AB). Èìååì:
z = 4x
2
+ (6 x)
2
16x 4(6 x) + 20
èëè
z = 5õ
2
24õ + 32.
Íàéäåì z ′ = 10õ 24 è èç z ′ = 0 èìååì 10õ 24 = 0, èëè
5
12
=x
Òàê êàê z ″ = (10õ 24)′ = 10 > 0, òî ïðè
5
12
=x
èìååì ìèíèìóì è
.
5
16
32
5
12
24
5
12
5
5
12
2
=+
⋅−
⋅=
=
zz
D

243
Íà êîíòóðå õ 2y = 0 èëè õ = 2y (ïðÿìàÿ ÎÂ) èìååì
z = 4(2y)
2
+ y
2
16 · 2y 4y+ 20 èëè z = 17y
2
36y + 20. Íàõîäèì
ïðîèçâîäíóþ z ′ = (17y
2
36y + 20)′ = 34y 36, ïðèðàâíèâàåì åå
ê íóëþ z ′ = 0 èëè 34y 36 = 0, îòñþäà
.
1
7
18
=y
Òàê êàê z ″ = (34y 36)′ = 34 > 0, òî â òî÷êå
17
18
=y
èìååì ìèíè-
ìóì è
.
17
16
17
18
17
18
203617
2
=+⋅−=
E
z
Íàéäåì çíà÷åíèÿ ôóíêöèè z â òî÷êàõ Î (0; 0), A (0; 6) è B (4; 2):
z
0
= 20; z
A
= 4 · 0 + 6
2
16 · 0 4 · 6 + 20 = 32;
z
B
= 4 · 4
2
+ 2
2
16 · 4 4 · 2 + 20 = 16.
Èç íàéäåííûõ çíà÷åíèé z
min
= 0; z
C
= 16;
;
5
16
=
D
z
;
17
16
=
E
z
z
0
= 20; z
A
= 32; z
B
= 16 âûáèðàåì íàèìåíüøåå è íàèáîëüøåå. Ïî-
ëó÷àåì, ÷òî z
íàèì
= 0, z
íàèá
= 32.
8. ÄÈÔÔÅÐÅÍÖÈÀËÜÍÛÅ ÓÐÀÂÍÅÍÈß
8.1. Óðàâíåíèÿ ïåðâîãî ïîðÿäêà
8.1.1. Íàéòè îáùåå ðåøåíèå óðàâíåíèÿ:
à) ó′ = e
4x 2y
. Ýòî äèôôåðåíöèàëüíîå óðàâíåíèå ïåðâîãî ïî-
ðÿäêà ñ ðàçäåëÿþùèìèñÿ ïåðåìåííûìè. Ðåøàåì åãî.
. ,
4224
dxedyeee
dx
dy
xyyx
=⋅=
−
Èíòåãðèðóåì
∫∫∫∫
== ).4(
4
1
)2(
2
1
èëè
4242
xdeydedxedye
xyxy
Òîãäà
Cee
xy
+
=
42
4
1
2
1
èëè
Cee
xy
+
=
42
2
1
åñòü îáùåå ðåøå-
íèå èñõîäíîãî óðàâíåíèÿ.
244
á) (3õ 5y) ó′= 5x + 3y.
Ðàçäåëèâ óðàâíåíèå íà õ
,3553
x
y
y
x
y
+=
′
−
ïîëó÷èëè îäíîðîäíîå äèôôåðåíöèàëüíîå óðàâíåíèå ïåðâîãî ïî-
ðÿäêà, êîòîðîå ñâåäåì ê óðàâíåíèþ ñ ðàçäåëÿþùèìèñÿ ïåðåìåí-
íûìè ââåäåíèåì ôóíêöèè
,
x
y
t
=
îòñþäà y = x · t è ó′ = t + x · t ′.
Ïîäñòàâëÿåì â èñõîäíîå óðàâíåíèå (3 5t)(t + xt ′) = 5 + 3t,
èëè
,
53
35
t
t
txt
−
+
=
′
+
èëè
,
53
35
tx
t
t
dx
dt
−
−
+
=
èëè
.
53
55
2
t
t
dx
dt
x
−
+
=
⋅
Ðàçäå-
ëÿåì ïåðåìåííûå
.
55
53
2
x
dx
t
t
dt
=
+
−
×èñëèòåëü äåëèì ïî÷ëåííî íà çíà-
ìåíàòåëü è èíòåãðèðóåì
∫∫∫
=
+
−
+
x
dx
t
tdt
t
dt
22
11
5
3
èëè
.
1
)1(
2
1
1
5
3
2
2
2
∫∫∫
=
+
+
−
+
x
dx
t
td
t
dt
Âñå èíòåãðàëû òàáëè÷íûå, òîãäà
Cxtt lnln)1ln(
2
1
tgarc
5
3
2
+=+−
èëè
.1ln tgarc
5
3
2
tcxt +=
Ïîäñòàâëÿåì ñþäà
,
x
y
t =
ïîëó÷èì
2
2
1ln tgarc
5
3
x
y
cx
x
y
+=
èëè
.ln tgarc
5
3
22
yxc
x
y
+=
Ýòî è áóäåò îáùåå ðåøåíèå èñõîäíîãî äèôôåðåíöèàëüíîãî
óðàâíåíèÿ.
â)
.
2
tgarc2)4(
2
x
yyx
=+
′
+
Ýòî ëèíåéíîå äèôôåðåíöèàëüíîå óðàâíåíèå ïåðâîãî ïîðÿäêà, êî-
òîðîå ðåøàåì ïîäñòàíîâêîé Áåðíóëëè y = u (x) · v (x) è ó′ = u ′v + uv′,
ïîñëå ÷åãî ïðèõîäèì ê ðåøåíèþ äâóõ äèôôåðåíöèàëüíûõ óðàâíå-
íèé ñ ðàçäåëÿþùèìèñÿ ïåðåìåííûìè.

245
Ïîäñòàâëÿåì y = uv, ó′ = u ′v + uv ′ â èñõîäíîå óðàâíåíèå
.
2
tg arc2))(4(
2
x
uvvuvux =+
′
+
′
+
Ãðóïïèðóåì
.
2
tg arc)2)4(()4(
22
x
uvvxvux =+
′
++
′
+
(à)
Ïóñòü
.2)4( èëè 02)4(
22
v
dx
dv
xvvx −=+=+
′
+
Ðàçäåëÿåì ïåðåìåííûå è èíòåãðèðóåì
2
4
2
x
dx
v
dv
+
−=
, èëè
∫∫
+
−= ,
2
2
22
x
dx
v
dv
èëè
,
2
tg arc
2
1
2ln
x
v ⋅−=
îòñþäà
2
tg arc
x
ev
−
=
(b)
Ïîäñòàâëÿåì ôóíêöèþ (b) â óðàâíåíèå (à)
2
tg arc)4(
2
tg arc
2
x
uex
x
=
′
⋅+
−
èëè
.
2
tg arc)4(
2
tg arc
2
x
dx
du
ex
x
=⋅+
−
Ðàçäåëÿåì ïåðåìåííûå è èíòåãðèðóåì
2
tg arc
4
2
tg arc
2
x
dxx
edu
x
+
⋅⋅=
èëè
∫∫
+
⋅= .
4
2
tg arc
2
tg arc
2
x
dxx
edu
x
(ñ)
×òîáû âçÿòü èíòåãðàë â ïðàâîé ÷àñòè, ââåäåì íîâóþ ïåðåìåí-
íóþ
,
2
arctg
x
t
=
òîãäà
dx
x
dt
2
1
2
1
1
2
⋅
+
=
èëè
.
4
2
1
2
x
dx
dt
+
=
Âûðàæåíèå (ñ) ïðèìåò âèä
.
2
1
dtteu
t
∫
=
(d)
246
Ýòîò èíòåãðàë áåðåòñÿ ïî ÷àñòÿì ïî ôîðìóëå
∫∫
⋅−=
,duvuvudv
íî ôóíêöèè u(x) è v(x) çäåñü ñîâñåì äðóãèå, ÷åì (b) è (ñ).
u = t, du = dt,
dtedvdtedv
tt
∫∫
==
,
èëè v = e
t
. (å)
Ñ èñïîëüçîâàíèåì âûðàæåíèé (å) èíòåãðàë (d) ñ èñïîëüçîâà-
íèåì ôîðìóëû èíòåãðèðîâàíèÿ ïî ÷àñòÿì çàïèøåòñÿ êàê
).(
2
1
)(
2
1
cetedteetu
tttt
+−=⋅−⋅=
∫
Ïîäñòàâëÿÿ ñþäà
,
2
tg arc
x
t
=
ïîëó÷èì:
.
2
tg arc
2
1
22
tg arctg arc
+−⋅= cee
x
u
xx
(f)
Ñëåäîâàòåëüíî, ðåøåíèå èñõîäíîãî äèôôåðåíöèàëüíîãî óðàâ-
íåíèÿ èìååò âèä:
+−⋅==
−
cee
x
euvy
xxx
222
tg arctg arctg arc
2
tg arc
2
1
èëè
.1
2
tg arc
2
1
2
tg arc
⋅+−=
−
x
ec
x
y
ã)
.
4
22
yxyy
x
=+
′
Ýòî, òàê íàçûâàåìîå, äèôôåðåíöèàëüíîå óðàâíåíèå Áåðíóëëè
âèäà
ó′ + p (x) · y = q (x) · y
n
.
Ñíà÷àëà åãî íóæíî ðàçäåëèòü íà y
n
, à çàòåì ââåñòè âñïîìîãà-
òåëüíóþ ôóíêöèþ z = y
n + 1
.
Äåëèì èñõîäíîå óðàâíåíèå íà ó
2
.
4
212
xy
x
yy =⋅+
′
⋅
−−
(à)
247
Ïóñòü z = y
2 + 1
= y
1
, íàéäåì
z′ = y
2
· ó′ èëè y
2
· ó′ = z′ (b)
Ïîäñòàâëÿåì ôóíêöèè (b) â óðàâíåíèå (à)
.
4
2
xz
x
z =⋅+
′
(ñ)
Ïîëó÷èëè ëèíåéíîå äèôôåðåíöèàëüíîå óðàâíåíèå, êîòîðîå
ðåøàåì ìåòîäîì Áåðíóëëè
z = uv, z′ = u′v + uv′. (d)
Ïîäñòàâëÿåì ôóíêöèè (d) â óðàâíåíèå (c)
2
4
)(
xuv
x
vuvu =+
′
+
′
−
è ãðóïïèðóåì
2
4
xuv
x
vuvu =
+
′
−+
′
−
èëè
.
4
2
xuv
x
vvu =
+
′
−+
′
−
(å)
Ïóñòü
,0
4
=+
′
− v
x
v
èëè
,
4
v
xdx
dv
=
èëè
,4
x
dx
v
dv
=
èëè
.4
∫∫
=
x
dx
v
dv
(f)
Îòñþäà
ln v = 4 ln x èëè v = x
4
. (g)
Ïîäñòàâëÿåì (g) â óðàâíåíèå (å)
x
4
· u′ = x
2
èëè ïðè õ ≠ 0
1
2
=−
dx
du
x
èëè
.
2
x
dx
du −=
Èíòåãðèðóåì
,
2
∫∫
−
−= dxxdu
èëè
,
1
1
C
x
u +
−
−=
−
èëè
.
1
C
x
u +=
248
Ýòó ôóíêöèþ è (g) ïîäñòàâëÿåì â (d)
+= C
x
xz
1
4
èëè z = x
3
+ Ñx
4
.
Èç âûðàæåíèÿ (b)
.
11
43
Cxx
z
y
+
==
Òàêèì îáðàçîì, ðåøåíèå èñõîäíîãî äèôôåðåíöèàëüíîãî óðàâ-
íåíèÿ èìååò âèä:
.
1
43
xcx
y
⋅+
=
8.1.2. Ñêîðîñòü ðîñòà áàíêîâñêîãî âêëàäà ïðîïîðöèîíàëüíà ñ
êîýôôèöèåíòîì ðàâíûì m = 3 âåëè÷èíå âêëàäà. Íàéòè çàêîí èç-
ìåíåíèÿ âåëè÷èíû âêëàäà ñî âðåìåíåì, åñëè ïåðâîíà÷àëüíàÿ ñóì-
ìà âêëàäà ñîñòàâëÿëà n = 2 ìèëëèîíîâ ðóáëåé.
Åñëè âåëè÷èíó âêëàäà îáîçíà÷èòü ÷åðåç J = J (t), ãäå t âðåìÿ,
òî ñêîðîñòü ðîñòà âêëàäà åñòü ïðîèçâîäíàÿ, ò.å.
dt
dJ
J
=
′
è îíà ïðî-
ïîðöèîíàëüíà âåëè÷èíå âêëàäà J ñ êîýôôèöèåíòîì ïðîïîðöèî-
íàëüíîñòè, ðàâíûì 3, ò.å.
.3J
dt
dJ
=
Ðàçäåëÿåì ïåðåìåííûå è èíòåãðèðóåì
dt
J
dJ
3=
èëè
∫∫
=
dt
J
dJ
3
ln J = 3t + C èëè J = e
3t + C
.
 íà÷àëüíûé ìîìåíò âðåìåíè, ò.å. ïðè t = 0 íà÷àëüíûé âêëàä
J
0
= 2 ìëí ðóá. Òîãäà
J
0
= e
3 · 0 + C
; e
C
= 2 è C · ln e = ln 2, ò.å. C = ln 2.
Îêîí÷àòåëüíî: J = e
3t + ln 2
èëè J = 2e
3t
.
249
8.2. Ëèíåéíûå óðàâíåíèÿ âûñøèõ ïîðÿäêîâ
8.2.1. Ðåøèòü çàäà÷ó Êîøè:
à) ó′″ 2ó″ 3ó′ = 0, y (0) = 0, ó′ (0) = 3, ó″ (0) = 1.
Ïîíèçèì ïîðÿäîê äèôóðàâíåíèÿ, îáîçíà÷èâ t = ó′, òîãäà t ′ = ó″,
t ″ = ó′″ è óðàâíåíèå èìååò âèä:
t ″ 2t ′ 3 = 0. (a)
Åãî õàðàêòåðèñòè÷åñêîå óðàâíåíèå r
2
2r 3 = 0, êîðíè êîòî-
ðîãî r
1
= 1, r
2
= 3. Òîãäà ðåøåíèå óðàâíåíèÿ (à) èìååò âèä:
xx
eÑeÑt
3
21
+=
−
èëè
,
3
11
xx
eÑeÑ
dx
d
y
y
+==
′
−
îòñþäà dy = (Ñ
1
e
x
+ Ñ
2
e
3x
) dx. Èíòåãðèðóÿ ýòî âûðàæåíèå, ïî-
ëó÷èì
.
3
1
3
3
21
ÑeÑeÑy
xx
++=
−
(b)
Ýòî åñòü îáùåå ðåøåíèå èñõîäíîãî äèôôåðåíöèàëüíîãî óðàâ-
íåíèÿ.
Èñïîëüçóÿ íà÷àëüíûå óñëîâèÿ, íàéäåì ïîñòîÿííûå Ñ
1
, Ñ
2
, Ñ
3
:
y′ = C
1
e
x
+ C
2
e
3x
, y ″ = C
1
e
x
+ 3C
2
e
3x
,
òîãäà
=+
=+
=++−
1.3
3,
,0
3
1
21
21
321
ÑÑ
ÑÑ
ÑÑÑ
Èç ýòîé ñèñòåìû
.
3
5
,1 ,2
321
=== ÑCC
À ÷àñòíîå ðåøåíèå èñõîäíîãî îäíîðîäíîãî äèôôåðåíöèàëü-
íîãî óðàâíåíèÿ ñ ïîñòîÿííûìè êîýôôèöèåíòàìè, óäîâëåòâîðÿþ-
ùåå íà÷àëüíûì óñëîâèÿì, áóäåò:
.
3
5
3
1
2
3
+⋅+−=
−
xx
ee
y

250
á) y ″ 6y ′ + 9y = (x + 1) e
4x
, y (0) = 1, y ′ (0) = 3. (a)
Íàõîäèì îáùåå ðåøåíèå îäíîðîäíîãî äèôôåðåíöèàëüíîãî
óðàâíåíèÿ (äèôóðà), ñîîòâåòñòâóþùåãî èñõîäíîìó äèôóðó (à):
y ″ 6y′ + 9y = 0. (b)
Åãî õàðàêòåðèñòè÷åñêîå óðàâíåíèå r
2
6r + 9 = 0, a êîðíè
r
1
= r
2
= 3. Òîãäà îáùåå ðåøåíèå äèôóðà (b) áóäåò:
y* = e
3x
(C
1
+ C
2
x). (c)
×àñòíîå ðåøåíèå èñõîäíîãî äèôóðà (à) áåðåì â âèäå:
,)(
4
x
eBAxy
⋅+=
(d)
òîãäà
,
)
(
4
44
xx
eBAxAe
y
++=
′
, )( 168
44
xx
eBAxAey
++=
′′
ïîäñòàâëÿåì â (à) è ãðóïïèðóåì: (2A + B) + Ax = 1 + x, îòñþäà,
ïðèðàâíÿâ êîýôôèöèåíòû ïðè îäèíàêîâûõ ñòåïåíÿõ õ, èìååì:
2A + B = 1 è A = 1,
ò.å. À = 1, B = 1, à âûðàæåíèå (d) ïðèíèìàåò âèä:
.)1(
4
x
exy
⋅−=
(å)
Ñóììèðóÿ (ñ) è (å), íàéäåì îáùåå ðåøåíèå íåîäíîðîäíîãî äèô-
ôåðåíöèàëüíîãî óðàâíåíèÿ (à):
.)1()(
43
21
xx
exexCCyyy
−++=+=
∗
(f)
Íàéäåì y′ = 3(Ñ
1
+ Ñ
2
x) e
3x
+ Ñ
2
e
3x
+ e
4x
+ 4 (õ 1) e
4x
è èñïîëü-
çóÿ íà÷àëüíûå óñëîâèÿ (à), èìååì:
−++=
−=
,4133
,11
21
1
ÑÑ
Ñ
îòñþäà Ñ
1
= 2, Ñ
3
= 0.
Íàéäåííûå çíà÷åíèÿ Ñ
1
è Ñ
2
ïîäñòàâëÿåì â (f) è ÷àñòíîå ðåøå-
íèå èñõîäíîãî äèôôåðåíöèàëüíîãî óðàâíåíèÿ èìååò âèä:
y = 2e
3x
+ (õ 1) e
4x
.
