Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
Подождите немного. Документ загружается.

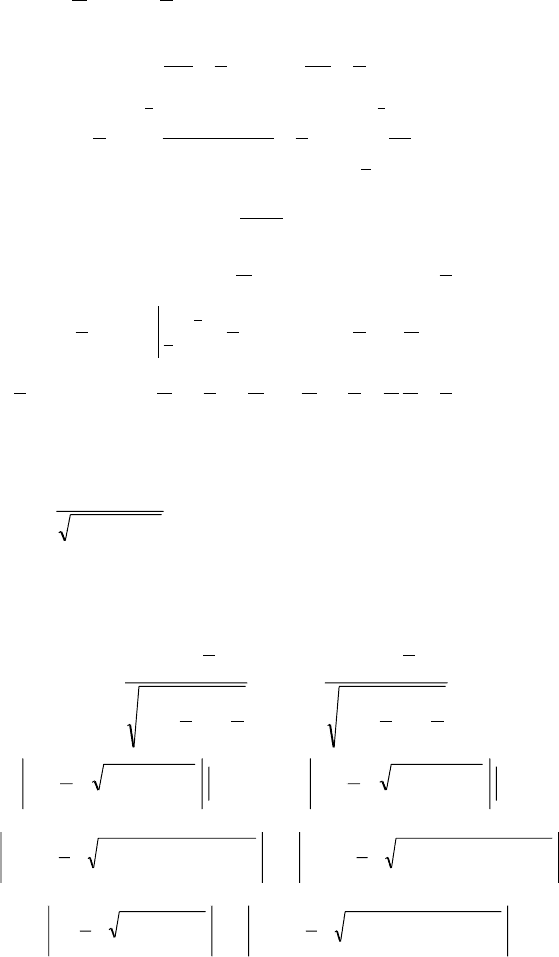
231
Ïóñòü
2
x
t
=
è
dxdt
2
1
=
, ñìåíèì ïðåäåëû èíòåãðèðîâàíèÿ:
∫∫
⇒=
+
=
=====
∞→∞→
2
4
2
arctg
1
2
Â
Â
Í
Í
lim
2
1
arctg)1(
lim
2
1
.
22
,1
2
2
2
bb
z
dz
tt
dt
J
b
x
t
x
t
bb
π
Ïóñòü z = arctg t, òîãäà
2
1
t
dt
dz
+
=
è íîâûå ïðåäåëû èíòåãðèðî-
âàíèÿ áóäóò:
−==
−=
−∞=
=
−=⇒
=====
∞→∞→
2ln
2
14
2
ln
2
1
4
ln
2
ln
2
1
4
ln arctgln
2
1
4
ln
2
arctgln lim
2
1
lnlim
2
1
.
2
arct arctg ,
4
1arctg arctg
2
4
arctg
BBÑÍ
π
ππππ
π
π
π
b
z
b
gtztz
bb
b
èíòåãðàë ñõîäèòñÿ.
á)
.
65
5
2
2
∫
+−
=
xx
dx
J
Íàéäåì òî÷êè, â êîòîðûõ ïîäèíòåãðàëüíàÿ ôóíêöèÿ òåðïèò
ðàçðûâ: x
2
5x + 6 = 0, x
1
= 2, x
2
= 3 è îáå òî÷êè ïðèíàäëåæàò
îòðåçêó èíòåãðèðîâàíèÿ [2; 5]. Òîãäà
=+−+−++−+−=
=
−
−
−
+
−
−
−
=
+
→
+
→
→
+
→
−
+
→
→
∫∫
5
3
2
0
-3
2
2
0
0
5
3
20
3
2
2
0
0
65
2
5
lnlim 65
2
5
lnlim
4
1
2
5
2
5
lim
4
1
2
5
2
5
lim
γ
γ
δ
ε
δ
ε
γ
γ
δ
ε
δ
ε
xxxxxx
x
xd
x
xd
J
=
++−++−+−+⋅−+−+
+
++−++−+−+−−−+−−=
→
→
→
6)3(5)3(
2
5
3 ln 6555
2
5
5 ln lim
6)2(5)2(
2
5
2 ln 6)3(5)3(
2
5
3 ln lim
22
0
22
0
0
γγγ
εεεδδδ
γ
δ
ε
232
)625ln(
2
2)625(
ln
2
1
ln
2
625
ln
2
1
ln
2
1
ln
2
5
3 ln 6
2
5
ln
2
5
2 ln
2
5
3 ln
+=
⋅+
=−
+
+
+−=−−++−−−=
èíòåãðàë ñõîäèòñÿ.
4.3. Ïðèëîæåíèÿ îïðåäåëåííûõ èíòåãðàëîâ
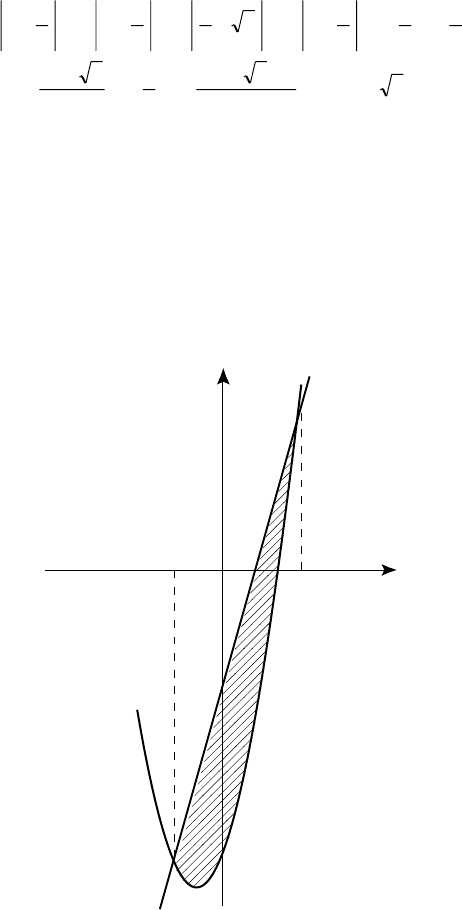
4.3.1. Íàéòè ïëîùàäü ôèãóðû, îãðàíè÷åííîé ëèíèÿìè, è ïî-
ñòðîèòü ñõåìàòè÷åñêèå ÷åðòåæè ôèãóð.
à) y = x
2
+ 2x 16, 4x y 8 = 0.
Èìååì ïàðàáîëó: y = (x + 1)
2
17 è ïðÿìóþ: 4õ y 8 = 0.
Íóæíî îïðåäåëèòü çàøòðèõîâàííóþ ïëîùàäü (ðèñ. 53).
Ðèñ. 53
2 0 4 x
y
233
Íàéäåì îáùèå òî÷êè ôèãóðû (ïðåäåëû èíòåãðèðîâàíèÿ):
−=
−+=
,84
,162
2
xy
xxy
îòñþäà õ
2
2õ 8 = 0 è õ
1
= 2, õ
2
= 4.
Ïëîùàäü ôèãóðû îïðåäåëÿåòñÿ êàê:
)åä. êâ.( 36)2(
2
1
)2()2(84
3
1
448
3
1
2
28 |28|
|)162()84(| |)()(|
3232
4
2
3
2
4
2
2
4
2
2
=
−+⋅−
⋅−+⋅=
=
−+=−+=
=−+−−=−=
−
−
−
∫
∫∫
x
x
xdxxx
dxxxxdxxxfS
b
a
ϕ
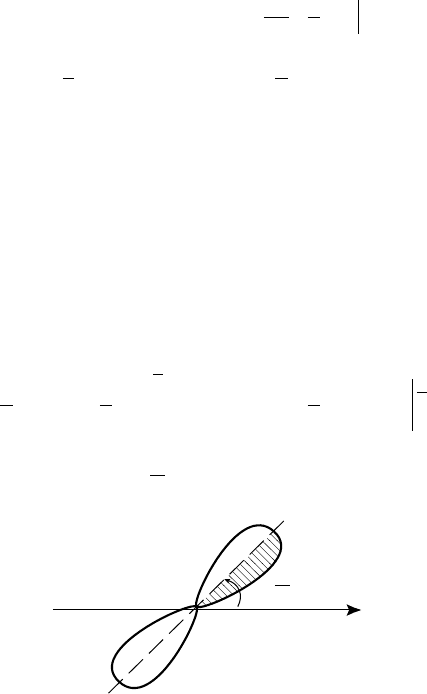
á) (x
2
+ y
2
)
2
= 18 xy.
Çàïèøåì ýòî óðàâíåíèå â ïîëÿðíîé ñèñòåìå êîîðäèíàò:
=
=
ϕρ
ϕρ
sin
cos
y
x
Ïîäñòàâèâ, ïîëó÷èì:
ρ
2
= 9 sin 2
ϕ.
Ïëîùàäü ëåìíèñêàòû (ðèñ. 54) ðàâíà ÷åòûðåì çàøòðèõîâàí-
íûì ïëîùàäÿì, òîãäà
åä.). (êâ. 90cos
2
cos 9
) 2cos(
2
1
92 2sin 94
2
1
2
1
4
42
1
0
0
2
=
−=
=−⋅⋅=⋅⋅==
∫∫
π
ϕϕϕϕρ
π
π
ϕ
ϕ
ddS
Ðèñ. 54
ρ
4
π
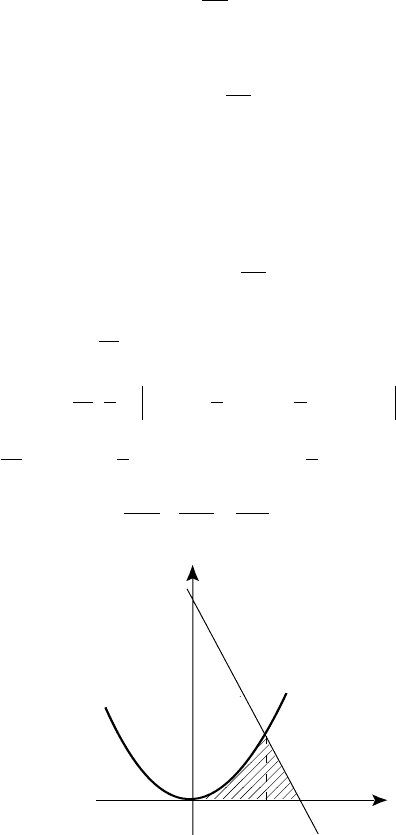
234
4.3.2. Íàéòè îáúåì òåëà âðàùåíèÿ âîêðóã îñè Îõ ôèãóðû, îã-
ðàíè÷åííîé ëèíèÿìè:
.0122 ;
4
;0
2
=−+== yx
x
yy
Íàõîäèì îáùèå òî÷êè ôèãóðû:
+−=
=
,122
,
4
2
xy
x
y
îòñþäà õ
2
+ 8õ 48 = 0 è õ
1
= 12, õ
2
= 4.
Çàøòðèõîâàííàÿ ôèãóðà (ðèñ. 55) âðàùàåòñÿ âîêðóã îñè Îõ.
Îáúåì òåëà âðàùåíèÿ îïðåäåëÿåòñÿ êàê:
åä.) (êóá.
15
352
3
32
5
64
436464
3
1
636666
3
1
44
80
36
2
1
12
3
1
4
5
1
16
)3612( 4
16
)122(
4
23235
6
4
234
0
5
6
4
2
4
0
4
6
4
4
0
6
4
2
2
2
2
4
0
2
π
ππ
π
π
π
π
π
π
ππππ
=+=
=
⋅+⋅−⋅−
⋅+⋅−⋅+⋅=
=
+⋅−+⋅=
=+−+=
=++
=+=
∫∫
∫∫ ∫∫
xxxx
dxxxdxx
dxxdx
x
dxydxyV
Ðèñ. 55
0 4 6
x
y
235
4.4. Ïðèáëèæåííûå âû÷èñëåíèÿ îïðåäåëåííûõ
èíòåãðàëîâ
4.4.1. Ðàçáèâàÿ îòðåçîê èíòåãðèðîâàíèÿ ñíà÷àëà íà 10 ðàâíûõ
÷àñòåé, à çàòåì íà 20 ÷àñòåé, íàéòè ïðèáëèæåííî èíòåãðàëû J
10
è J
20
. Îïðåäåëèòü òî÷íîñòü ñ ïîìîùüþ ðàçíîñòè
ε
= | J
10
J
20
| .
dxxJ
∫
−
+=
9
1
2
4
à) ïî ôîðìóëå òðàïåöèé;
á) ïî ôîðìóëå Ñèìïñîíà.
Ðåøåíèå. Èìååì ïîäèíòåãðàëüíóþ ôóíêöèþ
4
2
+=
xy
. Ñî-
ñòàâèì âñïîìîãàòåëüíóþ òàáëèöó.
Ïðè äåëåíèè Ïðè äåëåíèè
x
i
íà 10 ÷àñòåé íà 20 ÷àñòåé
4
2
+=
ii
x
y
4
2
+=
ii
x
y
1 1 5 y
0
= 2,23607 y
0
= 2,23607
0,5 0,25 4,25 y
1
= 2,06155
00 4y
1
= 2,0 y
2
= 2,0
0,5 0,25 4,25 y
3
= 2,06155
11 5 y
2
= 2,23607 y
4
= 2,23607
1,5 2,25 6,25 y
5
= 2, 5
24 8y
3
= 2,82843 y
6
= 2,82843
2,5 6,25 10,25 y
7
= 3, 20156
3913y
4
= 3,60555 y
8
= 3,60555
3,5 12,25 16,25 y
9
= 4,03113
41620y
5
= 4,47214 y
10
= 4,47214
4,5 20,25 24,25 y
11
= 4,92443
52529y
6
= 5,38516 y
12
= 5,38516
5,5 30,25 34,25 y
13
= 5,85235
63640y
7
= 6,32456 y
14
= 6,32456
6,5 42,25 46,25 y
15
= 6,80074
74953y
8
= 7,28011 y
16
= 7,28011
7,5 56,25 60,25 y
17
= 7,76209
86468y
9
= 8,24621 y
18
= 8,24621
8.5 72,25 76,25 y
19
= 8,73212
98185y
10
= 9,21954 y
20
= 9,21954
2
i
x
4
2
+
i
x
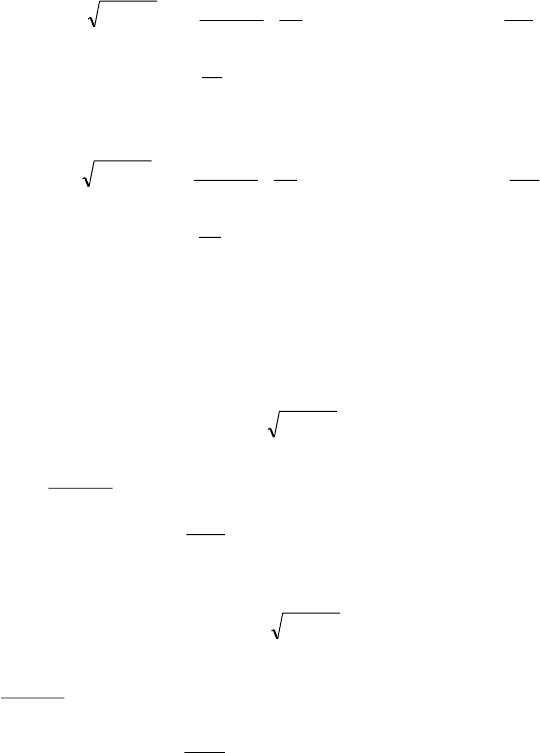
236
à) Ïî ôîðìóëå òðàïåöèé.
Ïðè äåëåíèè íà 10 ÷àñòåé:
.10604,4810604,48
10
10
2
...
2
10
)1(9
4
10
9821
0
9
1
2
10
=⋅=
=
++++++
−−
≈+=
∫
−
y
yyyy
y
dxxJ
Ïðè äåëåíèè íà 20 ÷àñòåé:
.01678,4803356,96
20
10
2
...
2
20
)1(9
4
20
191821
0
9
1
2
20
=⋅=
=
++++++
−−
≈+=
∫
−
y
yyyy
y
dxxJ
Òî÷íîñòü âû÷èñëåíèé îöåíèâàåì ñ ïîìîùüþ ðàçíîñòè:
ε
= | J
10
J
20
| = | 48,10604 48,01678 | = 0,08926.
á) Ïî ôîðìóëå Ñèìïñîíà.
Ïðè äåëåíèè íà 10 ÷àñòåé:
.98492,4795475,143
310
10
))...(2)...(4(
310
)1(9
4
108429310
9
1
2
10
=⋅
⋅
=
=+++++++++
⋅
−−
≈
≈+=
∫
−
yyyyyyyy
dxxJ
Ïðè äåëåíèè íà 20 ÷àñòåé:
.98702,4792215,287
320
10
))...(2)...(4(
320
)1(9
4
201816421917310
9
1
2
20
=⋅
⋅
=
=+++++++++++
⋅
−−
≈
≈+=
∫
−
yyyyyyyyyy
dxxJ
Òî÷íîñòü âû÷èñëåíèé:
e = | J
10
J
20
| = | 47,98492 47,98702 | = 0,0021.
Èçâåñòíî, ÷òî ïðè îäèíàêîâîì ÷èñëå òî÷åê ðàçáèåíèÿ ôîðìó-
ëà Ñèìïñîíà äàåò áîëåå òî÷íûé ðåçóëüòàò.
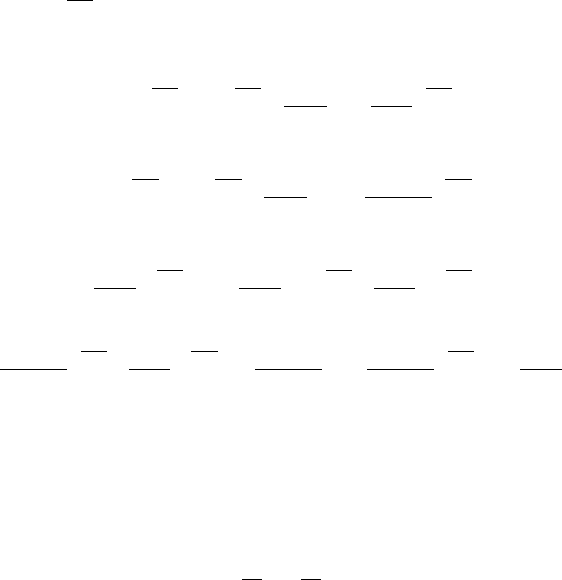
237
5. ÔÓÍÊÖÈÈ ÍÅÑÊÎËÜÊÈÕ ÏÅÐÅÌÅÍÍÛÕ
5.1. ×àñòíûå ïðîèçâîäíûå è äèôôåðåíöèàë
ôóíêöèè
5.1.1. Íàéòè ÷àñòíûå ïðîèçâîäíûå
,
x
z
′
,
y
z
′
è
xy
z
′′
ôóíêöèé:
à) z = (x 4)
2
y
2
+ x
4
(y + 2)
3
+ 8.
Íàõîäèì:
()
()
()
.)2(12)4(4)2(4)4(2
;)2(3)4(28)2()4(
;)2(4)4(28)2()4(
23332
2423422
3323422
++−=
′
++⋅−=
′
++−=
′
+++−=
′
++⋅−=
′
+++⋅−=
′
yxyxyxyxz
yxyxyxyxz
yxyxyxyxz
y
õy
y
y
x
x
á)
.
2
4
−
−
=
y
x
ez
Íàõîäèì:
.
2
4
1
)2(
1
)2(
4
2
1
)2(
1
2
1
2
1
2
1
;
)2(
4
2
4
;
2
1
2
4
2
4
22
2
4
2
4
2
2
4
2
4
2
4
2
4
2
2
4
2
4
2
4
2
4
2
4
−
−
+⋅
−
−=
−
−
−⋅⋅
−
+
−
−=
=
′
⋅
−
+⋅
′
−
=
′
⋅
−
=
′
−
−
−=
′
−
−
⋅=
′
=
′
−
=
′
−
−
⋅=
′
=
′
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
y
x
e
yy
x
e
y
e
y
e
y
e
y
e
y
z
e
y
x
y
x
eez
e
yy
x
eez
y
x
y
x
y
x
y
x
y
x
y
x
xy
y
x
y
x
y
x
y
y
x
y
x
y
x
x
5.1.2. Íàéòè äèôôåðåíöèàë dz ôóíêöèè:
z = sin
2
(4x
2
2y
2
).
Ïîëíûé äèôôåðåíöèàë îïðåäåëÿåòñÿ êàê:
.dy
y
z
dx
x
z
dz
∂
∂
+
∂
∂
=
õ
õ
ó
ó
ó
ó
ó

238
Íàéäåì ÷àñòíûå ïðîèçâîäíûå:
() ()
()
() ()
()
).28( sin4)22()24( 2sin
24)24( cos)24( sin2
)24( sin )24( sin2)24(sin
).48( sin824)24( 2sin
24)24( cos)24( sin2
)24( sin)24( sin2)24(sin
2222
222222
2222222
2222
222222
2222222
yxyyyx
yxyxyx
yxyxyxz
y
z
yxxxyx
yxyxyx
yxyxyxz
x
z
y
yy
y
x
xx
x
−⋅−=⋅−⋅−=
=
′
−⋅−⋅−=
=
′
−−=
′
−=
′
=
∂
∂
−=⋅⋅−=
=
′
−⋅−⋅−=
=
′
−⋅−=
′
−=
′
=
∂
∂
Òîãäà ïîëíûé äèôôåðåíöèàë áóäåò ðàâåí:
dz = 8x sin (8x
2
4y
2
) dx 4y sin (8x
2
2y
2
) dy =
= 4 sin (8x
2
4y
2
) (2xdx ydy).
5.1.3. Ïîêàçàòü, ÷òî ôóíêöèÿ z = y ln (4x
2
2y
2
) óäîâëåòâîðÿåò
óðàâíåíèþ
.
221
2
y
z
yx
yx
zz
=+
′′
Íàéäåì ÷àñòíûå ïðîèçâîäíûå:
() ()
()()()
()
.
24
4
)24( ln24
24
1
)24( ln
)24( ln24ln)24( ln
,
24
8
24
24
1
)24( ln
22
2
2222
22
22
222222
22
22
22
22
yx
y
yxyx
yx
yyx
yxyyxyyxyz
yx
xy
yx
yx
yyxyz
y
y
y
y
y
xx
x
−
−−=
′
−⋅
−
⋅+−=
=
′
−⋅+−⋅
′
=
′
−⋅=
′
−
=
′
−⋅
−
⋅=
′
−=
′
Ïîäñòàâëÿåì íàéäåííûå ÷àñòíûå ïðîèçâîäíûå â óðàâíåíèå:
.
)24( ln2)24( ln2
;
)24( ln2
24
8)24( ln2
24
8
;
)24( ln2
24
4
)24ln(
2
24
81
2222
22
22
22
22
2
22
22
2
22
22
y
yx
y
yx
y
yx
yx
y
y
yx
yx
y
y
yxy
yx
y
yx
y
yx
xy
x
−
=
−
−
=
−
−
−
+
−
−
=
−
−−+
−
⋅
Ïîëó÷èëè òîæäåñòâî.
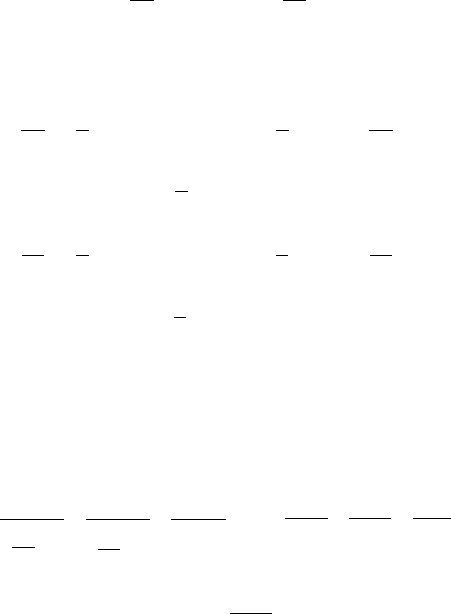
239
5.2. Ïðèëîæåíèÿ ÷àñòíûõ ïðîèçâîäíûõ
5.2.1. Ñîñòàâèòü óðàâíåíèå êàñàòåëüíîé ïëîñêîñòè è óðàâ-
íåíèå íîðìàëè ê ïîâåðõíîñòè 4z = xy 2x 4y + 8 â òî÷êå
Ì (4; 2; 8).
Ðåøåíèå. Ïðîâåðèì ïðèíàäëåæèò ëè òî÷êà Ì ïîâåðõíîñòè:
4 · 8 = (4) · (2) 2 · (4) 4(2) + 8, 32 = 32,
ñëåäîâàòåëüíî, òî÷êà Ì ïðèíàäëåæèò ïîâåðõíîñòè.
Óðàâíåíèå êàñàòåëüíîé ïëîñêîñòè èìååò âèä:
).()(
Ì
Ì
Ì
Ì
Ì
y
y
y
z
õõ
x
z
zz
−
∂
∂
+−
∂
∂
=−
Íàéäåì çíà÷åíèÿ ÷àñòíûõ ïðîèçâîäíûõ â òî÷êå Ì:
,2)44(
4
1
);4(
4
1
)842(
4
1
;1)22(
4
1
);2(
4
1
)842(
4
1
−=−−=
=
∂
∂
−=
′
+−−=
∂
∂
−=−−=
=
∂
∂
−=
′
+−−=
∂
∂
Ì
Ì
y
z
x
y
xx
y
y
z
x
z
y
y
xx
y
x
z
è ïîäñòàâèì â óðàâíåíèå êàñàòåëüíîé ïëîñêîñòè:
z 8 = (1) (x (4)) + (2)(y (2)) èëè x + 2y + z = 0.
Óðàâíåíèå íîðìàëè áåðåì â âèäå:
,
1−
−
=
∂
∂
−
=
∂
∂
−
Ì
Ì
Ì
Ì
Ì
zz
y
z
y
y
x
z
xx
èëè
,
1
8
2
2
1
4
−
−
=
−
+
=
−
+ zyx
èëè
.8
2
2
4 −=
+
=+ z
y
x
õ
ó
240
5.2.2. Íàéòè ãðàäèåíò è ïðîèçâîäíóþ ïî íàïðàâëåíèþ
jia 24 −=
ôóíêöèè z = ln (4x
2
+ 2y
2
) â òî÷êå À (2; 4).
Ðåøåíèå. Ãðàäèåíò ôóíêöèè z = f (x, y) ðàâåí:
. grad j
y
z
x
z
z ⋅
∂
∂
+
∂
∂
=
ι
Íàéäåì ÷àñòíûå ïðîèçâîäíûå:
() ()
() ()
2222
22
22
22
2222
22
22
22
2
2
24
22
24
24
1
)24( ln
,
2
4
24
8
24
24
1
)24( ln
yx
y
yx
y
yx
yx
yx
y
z
yx
x
yx
x
yx
yx
yx
x
z
yy
xx
+
=
+
⋅
′
+⋅
+
=
′
+=
∂
∂
+
=
+
=
′
+⋅
+
=
′
+=
∂
∂
è èõ çíà÷åíèÿ â òî÷êå À (2; 4):
.
3
1
4)2( 2
42
;
3
1
4)2( 2
)2( 4
2222
=
+
⋅
=
∂
∂
−=
+
=
∂
∂
A
A
y
z
x
z
Òîãäà ãðàäèåíò â òî÷êå À ðàâåí:
()
.
3
1
3
1
grad jz
À
+−=
ι
Ïðîèçâîäíàÿ ôóíêöèè z â íàïðàâëåíèè âåêòîðà
à
âû÷èñëÿåò-
ñÿ ïî ôîðìóëå:
.sincos
αα
⋅
∂
∂
+⋅
∂
∂
=
∂
∂
y
z
x
z
a
z
Íàéäåì íàïðàâëÿþùèé êîñèíóñ âåêòîðà
à
:
,
5
2
20
4
)2(4
4
cos
22
==
−+
=
α
òîãäà
.
5
1
5
4
1
5
2
1cos1sin
2
2
=−=
−=−=
αα
Ñëåäîâàòåëüíî,
.
15
5
53
1
5
1
3
1
5
2
3
1
−=−=⋅+⋅−=
∂
∂
A
a
z
