Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
Подождите немного. Документ загружается.

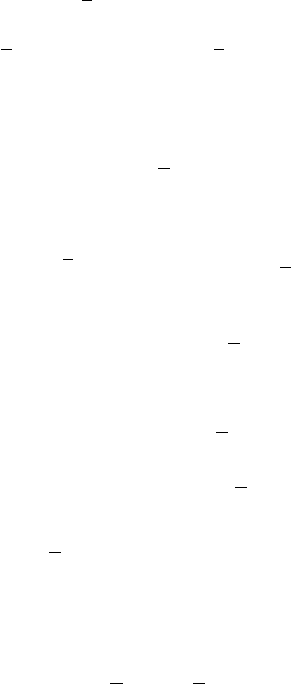
251
â) y″ + 4y = sin x, y (0) = 0, ó′ (0) = 3. (a)
Îäíîðîäíîå äèôóðàâíåíèå
y″ + 4y = 0 (b)
èìååò õàðàêòåðèñòè÷åñêîå óðàâíåíèå r
2
+ 4 = 0, a åãî êîðíè áóäóò
r
1,2
= ± 2i Òîãäà îáùåå ðåøåíèå äèôóðà (b) áóäåò:
y* = Ñ
1
sin 2x + Ñ
2
cos 2x. (c)
×àñòíîå ðåøåíèå äèôóðà (à) èùåì â âèäå:
.cossin xBxAy +=
(d)
Îïðåäåëèâ xBxñosA
y
sin −=
′
è
xBxAy cos sin −−=
′′
è ïîä-
ñòàâèâ â (à), ïîñëå ãðóïïèðîâêè èìååì
3À sin x + 3Â cos x = sin x,
îòñþäà 3À = 1, 3Â = 0 èëè
3
1
=A
è Â = 0. Ïîäñòàâëÿÿ À è Â â (d)
è ñóììèðóÿ ñ (ñ), íàéäåì îáùåå ðåøåíèå äèôóðà (à):
.sin
3
1
2cos2sin
21
xxCxCyyy ++=+=
∗
(å)
Íàéäåì
xxCxCy cos2sin22cos2
3
1
21
+−=
′
è, èñïîëüçóÿ íà-
÷àëüíûå óñëîâèÿ (à), èìååì
⋅+⋅−⋅=
⋅+⋅+⋅=
,1
3
1
02123
,0
3
1
100
21
21
CC
CC
îòñþäà Ñ
2
= 0,
.
3
4
1
=C
Ïîäñòàâëÿÿ íàéäåííûå Ñ
1
è Ñ
2
â (å), áóäåì èìåòü ðåøåíèå èñ-
õîäíîãî äèôôåðåíöèàëüíîãî óðàâíåíèÿ (à), óäîâëåòâîðÿþùåãî
íà÷àëüíûì óñëîâèÿì:
.sin
3
1
2sin
3
4
xxy +=
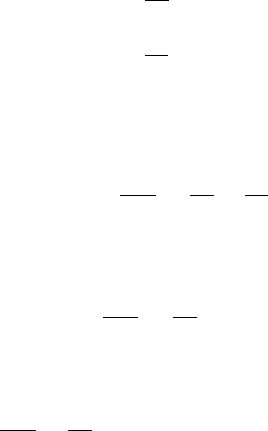
252
8.3. Ñèñòåìû ëèíåéíûõ óðàâíåíèé
8.3.1. Ðåøèòü ñèñòåìó ëèíåéíûõ óðàâíåíèé
+=
−=
,24
,42
yx
dt
dy
yx
dt
dx
ñ íà÷àëüíûìè óñëîâèÿìè õ (0) = 1, ó(0) = 2.
Ïðîäèôôåðåíöèðóåì ïåðâîå óðàâíåíèå ñèñòåìû
dt
dy
dt
dx
dt
xd
42
2
2
−=
è ïîäñòàâèì â íåãî
t
y
′
èç 2-ãî óðàâíåíèÿ ñèñòåìû
,8162
2
2
yx
dt
dx
dt
xd
−−=
à â ýòî óðàâíåíèå ïîäñòàâèì ó èç 1-ãî óðàâíåíèÿ ñèñòåìû, èìååì:
0204
2
2
=+− x
dt
dx
dt
xd
èëè õ″ - 4õ′ + 20õ = 0. (à)
Åãî õàðàêòåðèñòè÷åñêîå óðàâíåíèå r
2
4r + 20 = 0, êîðíè
êîòîðîãî r = 2 ± 4i. Òîãäà äèôôåðåíöèàëüíîå óðàâíåíèå (à) èìååò
ðåøåíèå:
x = e
2t
(Ñ
1
sin 4t + Ñ
2
cos 4t). (b)
Ïîäñòàâëÿÿ ýòî ðåøåíèå â 1-îå óðàâíåíèå ñèñòåìû, ïîñëå ãðóï-
ïèðîâàíèÿ íàéäåì, ÷òî
y = e
2t
(Ñ
1
cos 4t + Ñ
2
sin 4t). (c)
Ïîäñòàâëÿÿ â (b) è (ñ) íà÷àëüíûå óñëîâèÿ, îïðåäåëèì, ÷òî
⋅+⋅⋅=
⋅+⋅⋅=
),01(12
),10(11
21
21
ÑÑ
ÑÑ
îòñþäà Ñ
1
= 2, Ñ
2
= 1.

253
Ïîäñòàâèâ ýòè êîíñòàíòû â (b) è (ñ), íàéäåì ðåøåíèå èñõîä-
íîé ñèñòåìû äèôôåðåíöèàëüíûõ óðàâíåíèé
x = e
2t
(2 sin 4t + cos 4t),
y = e
2t
(sin 4t + 2 cos 4t).
9. ÐßÄÛ
9.1. ×èñëîâûå ðÿäû
9.1.1. Èññëåäîâàòü íà ñõîäèìîñòü ðÿäû ñ ïîëîæèòåëüíûìè
÷ëåíàìè:
à)
.
221
323
1
2
2
∑
∞
=
+−
+−
k
kk
kk
Ðàññìîòðèì îáùèé ÷ëåí
.
12
3
2
2
+−
+−
=
knk
nkmk
a
k
Ïðèìåíèì íåîáõîäèìûé ïðèçíàê ñõîäèìîñòè ÷èñëîâîãî ðÿäà.
Åñëè
,0lim =
∞→
k
k
a
òî ðÿä âîçìîæíî ñõîäèòñÿ, åñëè
,0lim ≠
∞→
k
k
a
òî
ðÿä ðàñõîäèòñÿ.
Äëÿ íàøåãî ïðèìåðà:
.
12
3
lim
2
2
∞
∞
=
+−
+−
=
∞→
knk
nkmk
J
k
Èìååì íåîïðåäåëåííîñòü, ÷èñëèòåëü è çíàìåíàòåëü äåëèì íà k
2
,0
00
00
12
3
12
3
lim
2
2
≠=
+−
+−
=
∞
+
∞
−
∞
+
∞
−
=
+−
+−
=
∞→
n
m
n
m
n
n
m
k
k
n
k
k
n
m
J
k
òàê êàê ïî óñëîâèþ m ≠ 0.
Ñëåäîâàòåëüíî, ó âñåõ ñòóäåíòîâ ðÿä ðàñõîäèòñÿ, òàê êàê
íå âûïîëíÿåòñÿ íåîáõîäèìûé ïðèçíàê ñõîäèìîñòè ÷èñëîâîãî
ðÿäà.
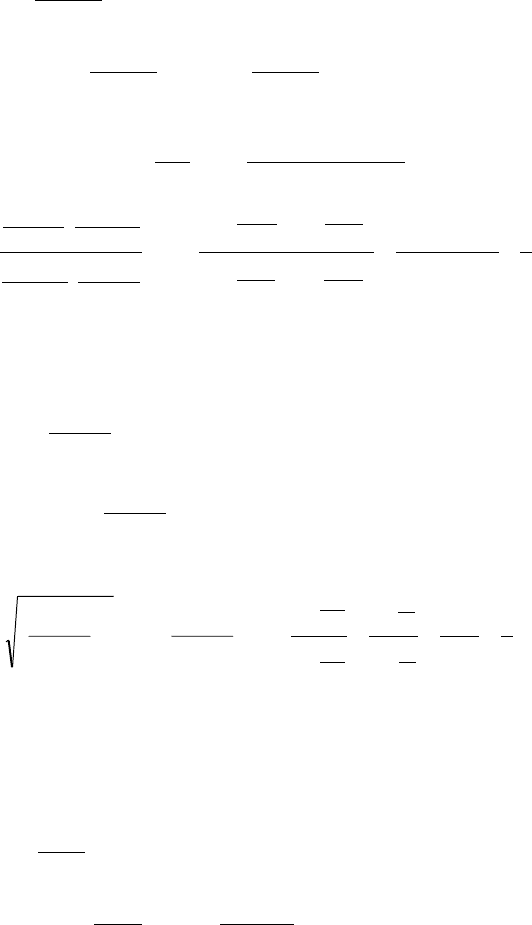
254
á)
∑
∞
=
+
+
+
+
1
3
4
.
23
12
k
k
k
Èìååì
23
12
3
4
+
+
+
+
=
k
k
k
a
è
.
23
12
4
5
1
+
+
+
+
+
=
k
k
k
a
Èññëåäóåì ñõîäèìîñòü ðÿäà ïî ïðèçíàêó Äàëàìáåðà:
.1
3
2
0)(1 )03(
0)(1 )02(
2
1
1
3
2
3
3
2
1
2
1
2
lim
2
12
3
23
3
23
2
12
lim
)12( )23(
)23( )12(
lim lim
43
34
4
4
3
4
3
3
4
5
44
35
1
<=
++
++
=
+
+
+
+
=
+
⋅
+
+
⋅
+
=
=
++
++
==
++
++
∞→
+
+
+
+
+
+
+
+
∞→
++
++
∞→
+
∞→
kk
kk
k
k
k
k
k
k
k
k
k
k
kk
kk
k
k
k
k
a
a
l
Ñëåäîâàòåëüíî, ðÿä ñõîäèòñÿ.
â)
∑
∞
=
+
+
1
2
2
.
35
23
k
k
k
k
Èìååì
.
35
23
2
2
k
k
k
k
a
+
+
=
Ïî ïðèçíàêó Êîøè èìååì:
,1
5
3
05
03
3
5
2
3
3
5
2
3
lim
35
23
lim
35
23
lim
2
2
2
2
2
2
<=
+
+
=
∞
+
∞
+
=
+
+
=
+
+
=
+
+
∞→∞→∞→
k
k
k
k
k
k
kk
k
k
k
ñëåäîâàòåëüíî, ðÿä ñõîäèòñÿ. Ïðèìåð ñêîíñòðóèðîâàí òàê, ÷òî
êîýôôèöèåíò (m + n) ïåðåä k
2
â çíàìåíàòåëå áîëüøå, ÷åì êîýôôè-
öèåíò m ïåðåä k
2
â ÷èñëèòåëå, à ïîýòîìó âñåãäà ïðåäåë áóäåò ìåíü-
øå åäèíèöû, ò.å. ðÿä áóäåò ñõîäÿùèéñÿ.
ã)
∑
∞
=
+
1
.
14
! )2(
k
k
k
Èìååì
.
14
! )22(
14
! )2(
1
1
,
+
+
=
+
=
+
+
k
k
k
k
kk
aa
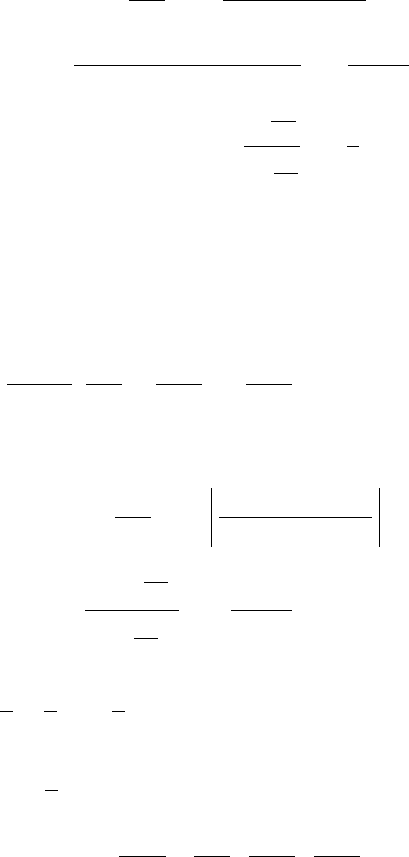
255
Èññëåäóåì ñõîäèìîñòü ðÿäà ïî ïðèçíàêó Äàëàìáåðà:
.1
4
1
4
1
4
4
1
1
lim)22( )12( lim
14
14
lim
2...21
)22()12(2...21
lim
! )2( )14(
)14( ! )22(
limlim
1
1
1
>∞=⋅∞=
+
+
⋅++=
=
+
+
⋅
⋅⋅⋅
+⋅+⋅⋅⋅⋅
=
=
+
++
==
∞→∞→
+
∞→∞→
+
∞→
+
∞→
k
k
kk
k
k
kk
k
k
k
k
k
k
kk
k
kkk
k
k
a
a
l
Ñëåäîâàòåëüíî, ðÿä ðàñõîäèòñÿ
9.2. Ñòåïåííûå ðÿäû
9.2.1. Íàéòè îáëàñòü ñõîäèìîñòè ñòåïåííîãî ðÿäà:
à)
...
12
2
12
2
12
2
:
12
2
3
3
6
2
2
42
1
2
+
+
+
+
+
+
+
⋅
∑
∞
=
xxx
x
k
k
kk
Ñîãëàñíî ïðèçíàêó Äàëàìáåðà èñêîìûé ðÿä ñõîäèòñÿ ïðè òåõ
çíà÷åíèÿõ õ, äëÿ êîòîðûõ:
1, ||2 ||
)02(
)01(4
||
2
1
2
2
1
1 2
lim
2)12(
)12(2
limlim
2
21
1)1(2
1
<=
+
+
=
+
+
=
=
+
+
==
∞→
+
++
∞→
+
∞→
xxx
x
x
a
a
l
k
k
k
kkk
kkk
k
k
k
k
ò.å.
.
2
1
2
1
2
1
, ||
<<< xx
Èññëåäóåì ñõîäèìîñòü ðÿäà íà êîíöàõ èíòåðâàëà.
Ïðè
2
1
−=x
ïîëó÷àåì ÷èñëîâîé ðÿä
∑
∞
=
+
+
−
+
+
+
−
+
−
1
3
3
2
2
. ...
12
2
12
2
12
2
:
12
2
)1(
k
k
k
k
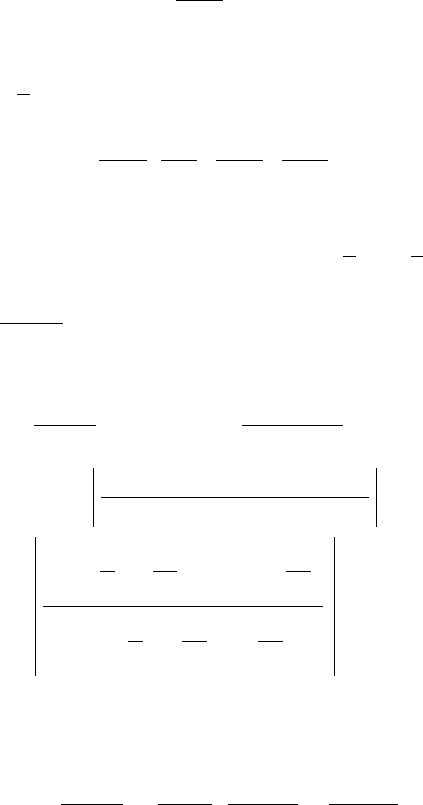
256
Ýòî çíàêî÷åðåäóþùèéñÿ, äëÿ êîòîðîãî
,01
12
2
lim ≠=
+
∞→
k
k
k
ò.å. ïî ïðèçíàêó Ëåéáíèöà ðÿä ðàñõîäèòñÿ.
Ïðè
2
1
=x
èìååì ÷èñëîâîé ðÿä ñ ïîëîæèòåëüíûìè ÷ëåíàìè
, ...
12
2
12
2
12
2
:
12
2
3
3
2
2
1
+
+
+
+
+
+
∑
∞
=
k
k
k
êîòîðûé ðàñõîäèòñÿ, òàê êàê ïðåäåë îáùåãî ÷èñëà íå ðàâåí íóëþ.
Èòàê, îáëàñòü ñõîäèìîñòè äàííîãî ðÿäà
.
2
1
2
1
<<− x
á)
∑
∞
=
−
+
+
1
4
3
.
23
12
)2(
k
k
x
k
k
Ïðèìåíèì ïðèçíàê Äàëàìáåðà:
;)2(
2)1(3
1)1(2
;)2(
23
12
1
4
3
1
4
3
+
+
−
++
++
=−
+
+
=
k
k
k
k
x
k
k
ax
k
k
a
.1 |2|
1
2
21
1 3
2
3 )2(
11
1 2
lim
)2)(12( )2)13((
)23()2( )1)12((
lim
34
4
43
3
34
413
<−=
+
+
+
+−
+
+
=
=
−+++
+−++
=
∞→
+
∞→
x
kk
k
k
x
k
k
xkk
kxk
l
k
k
k
k
Îòñþäà çàêëþ÷àåì, ÷òî ðÿä ñõîäèòñÿ ïðè 1 < x 2 < 1, èëè
1 < x < 3.
Ïðè õ = 1 ïîëó÷àåì çíàêî÷åðåäóþùèéñÿ ðÿä
, ... ;
233
132
;
223
122
;
213
112
:
23
12
)1(
1
4
3
4
3
4
3
∑
∞
=
+⋅
+⋅
+⋅
+⋅
+⋅
+⋅
−
+
+
k
k
k
k
êîòîðûé ñõîäèòñÿ ïî ïðèçíàêó Ëåéáíèöà, òàê êàê åãî ÷ëåíû óáû-
âàþò, à ïðåäåë îáùåãî ÷ëåíà ïðè k → ∞ ðàâåí íóëþ.

257
Ïðè õ = 3 èìååì ÷èñëîâîé ðÿä
∑
∞
=
++
++
+
+
+
+
1
4
3
4
3
4
3
... ;
2)1(3
1)1(2
;
23
12
; ... ;
245
55
;
50
17
;
5
3
:
23
12
k
k
k
k
k
k
k
Ñðàâíèì åãî ñ ãàðìîíè÷åñêèì ðÿäîì
, ...
1
...
3
1
2
1
1 +++++
k
êîòîðûé ðàñõîäèòñÿ.
Âîñïîëüçóåìñÿ ïðåäåëüíûì ïðèçíàêîì ñðàâíåíèÿ. Òàê êàê
ïðåäåë
,
2
3
)12(
23
limlim
3
4
=
+
+
=
∞→∞→
kk
k
b
a
k
k
k
k
ëåæèò ìåæäó 0 è ∞, òî îáà ðÿäà ðàñõîäÿòñÿ, ò.å. ïðè õ = 3 èñõîä-
íûé ðÿä ðàñõîäèòñÿ.
Èòàê, îáëàñòü ñõîäèìîñòè äàííîãî ðÿäà: 1 ≤ õ < 3.
b)
...
! 6
2
! 4
2
! 2
2
:
! )2(
2
3
3
2
2
1
+++
⋅
∑
∞
=
xxx
k
x
k
kk
Ïðèìåíèì ïðèçíàê Äàëàìáåðà:
;
! )22(
2
;
! )2(
2
11
1
+
⋅
=
⋅
=
++
+
k
x
a
k
x
a
kk
k
kk
k
.10
264
1
lim||2
)22()12(2...21
2...21
lim||2
2 ! )22(
! )2(2
lim
2
11
<=
++
=
=
+⋅+⋅⋅⋅⋅
⋅⋅⋅
=
⋅⋅+
⋅⋅
=
∞→
∞→
++
∞→
kk
x
kkk
k
x
xk
kx
l
k
k
kk
kk
k
Ñëåäîâàòåëüíî, ïðè ëþáîì êîíå÷íîì õ ïî ïðèçíàêó Äàëàìáå-
ðà äàííûé ðÿä àáñîëþòíî ñõîäèòñÿ. Îáëàñòü ñõîäèìîñòè ðàññìàò-
ðèâàåìîãî ðÿäà åñòü âñÿ ÷èñëîâàÿ îñü.

258
9.2.2. Ðàçëîæèòü ôóíêöèþ f (x) â ðÿä Òåéëîðà â îêðåñòíîñòè
òî÷êè õ
0
:
à)
;
4
)(
+
=
x
x
xf
õ
0
= 3.
Çàïèøåì ôóíêöèþ â âèäå:
.
4
4
1)( ;
4
4)4(
)(
+
−=
+
−+
=
x
xf
x
x
xf
Âû÷èñëèì çíà÷åíèÿ äàííîé ôóíêöèè è åå ïîñëåäîâàòåëüíûõ
ïðîèçâîäíûõ ïðè õ
0
= 3:
.
7
!
4)1()3(,)4( ! 4)1()(
,
7
!3
4)3(,)4( 24)(
,
7
!2
4)3(,)4( 8)(
,
7
4
)3(,)4( 4)(
,
7
3
)3(,)4( 41)(
1
1)()1(1)(
4
4
3
3
2
2
1
+
++−+
−
−
−
−
⋅⋅−=+⋅⋅⋅−=
⋅=
′′′
+=
′′′
⋅−=
′′
+−=
′′
=
′
+=
′
=+−=
n
nnnnn
n
fxnxf
fxxf
fxxf
fxxf
fxxf
LLLLLLLLLLLLLLLLLLLLLLLLL
Ïîäñòàâëÿÿ ïîëó÷åííûå çíà÷åíèÿ â îáùåå âûðàæåíèå ðÿäà
Òåéëîðà äëÿ ïðîèçâîëüíîé ôóíêöèè f(x) = f(x
0
) + f ′(x
0
)(x x
0
) +
+
2
0
0
)(
! 2
)(
xx
x
f
−
′′
+
3
0
0
)(
! 3
)(
xx
xf
−
′′′
+ ... +
n
n
xx
n
x
f
)(
!
)(
0
0
)(
−
...,
ïîëó÷èì
...)3(
7
4
)1(...)3(
7
4
)3(
7
4
)3(
7
4
7
3
4
1
13
4
2
32
+−−+−−+−−−+=
+
+
+
n
n
n
xxxx
x
x
á)
∫
−
=
x
x
dx
x
f
2
0
3
1
)(
, õ
0
= 0.
Âîçüìåì òàáëè÷íîå ðàçëîæåíèå
,1 | | , ...)1(...1
1
1
32
<+−++−+−=
+
ttttt
t
nn
â êîòîðîì ïîëîæèì t = x
3
.
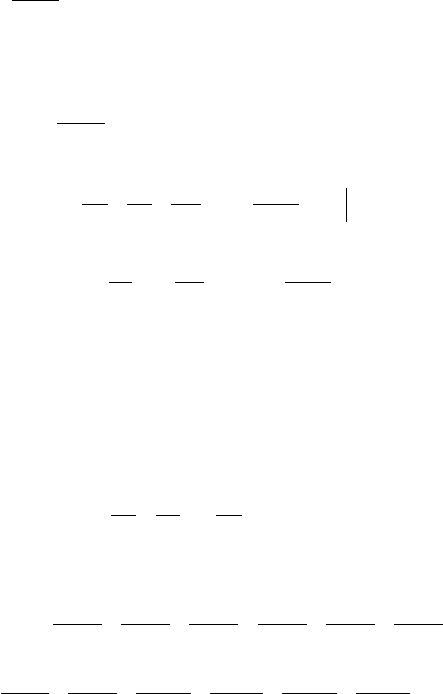
259
Èìååì
.1 | | , ......1
1
1
3963
3
<++++++=
−
xxxxx
x
n
Èíòåãðèðóåì ýòîò ðÿä:
...
13
2
...
10
2
7
2
42
...
13
...
1074
)......1(
1
)(
13
13
10
10
7
7
4
2
0
131074
2
0
3963
2
0
3
+
+
+++++=
=
+
+
+++++=
=++++++=
−
=
+
+
+
∫∫
n
n
x
n
x
n
x
x
n
xxxx
n
xxxx
x
dxxxxx
x
dx
x
f
Ïîëó÷èëè èñêîìîå ðàçëîæåíèå.
9.2.3. Ñ ïîìîùüþ ðàçëîæåíèÿ â ðÿä âû÷èñëèòü ïðèáëèæåííî ñ
òî÷íîñòüþ 0,001 çíà÷åíèÿ:
à) å
3
.
Áåðåì ðàçëîæåíèå ôóíêöèè f (x) = e
x
â ðÿä Òåéëîðà:
)( , ...
!
...
! 3! 2
1
32
∞<<∞+++++= x
n
xxx
xe
n
x
è ïîäñòàâëÿåì â íåãî õ = 3:
=
−
+
−
+
−
+
−
+
−
+
−
+
+
−
+
−
+
−
+
−
+
−
+
−
+−=
! 31
)3(
! 12
)3(
! 11
)3(
! 01
)3(
! 9
)3(
! 8
)3(
! 7
)3(
! 6
)3(
! 5
)3(
! 4
)3(
! 3
)3(
! 2
)3(
31
1312111098
765432
3
e
=2 + 4,5 4,5 + 3,375 2,025 + 1,012 0,434 + 0,163 0,054 +
+0,016 0,004 + 0,001 0,00026.
Ïîëó÷åííûé ðÿä çíàêî÷åðåäóþùèéñÿ. Ïîýòîìó, îãðàíè÷èâà-
ÿñü ïåðâûìè äâåíàäöàòüþ ÷ëåíàìè ðÿäà, ìû ïîëó÷èì îøèáêó
0,00026 < 0,001.
Ñëåäîâàòåëüíî, e
3
= 0,05.
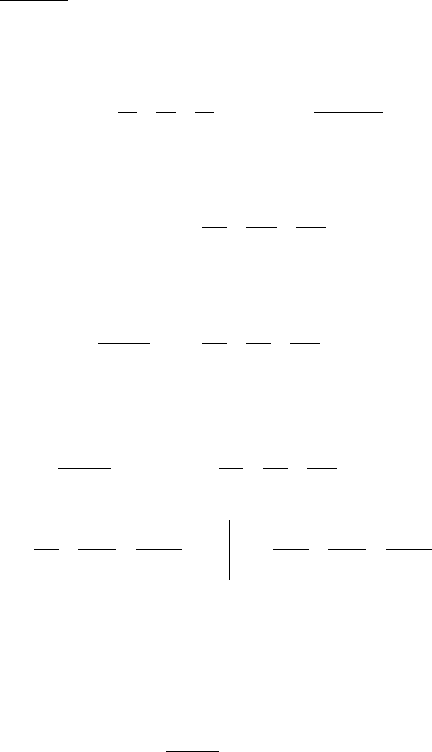
260
á)
.
)( sin
8,0
0
2
dx
x
x
∫
Âîçüìåì òàáëè÷íîå ðàçëîæåíèå:
...
! )12(
)1( ...
! 7! 5! 3
sin
12753
+
+
−++−+−=
+
n
tttt
tt
n
n
è ïîäñòàâèì â íåãî t = x
2
:
...
! 7! 5! 3
sin
14106
22
+−+−=
xxx
xx
Ðàññìîòðèì ôóíêöèþ:
...
! 7! 5! 3
sin
13952
+−+−=
xxx
x
x
x
è ïðîèíòåãðèðóåì åå:
.00009,0007,032,0
! 510
6,0
! 36
8,0
2
8,0
...
! 510! 362
...
! 7! 5! 3
sin
1062
0,8
0
1062
8,0
0
1395
8,0
0
2
+−=
=
⋅
+
⋅
−=
+
⋅
+
⋅
−=
=
+−+−=
∫∫
xxx
dx
xxx
xdx
x
x
Îãðàíè÷èâàÿñü ïåðâûìè äâóìÿ ÷ëåíàìè ðÿäà (îøèáêà ïðè ýòîì
íå ïðåâîñõîäèò 0,00009 < 0,001) èìååì îêîí÷àòåëüíî:
.313,0
sin
8,0
0
2
=
∫
dx
x
x
