Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
Подождите немного. Документ загружается.

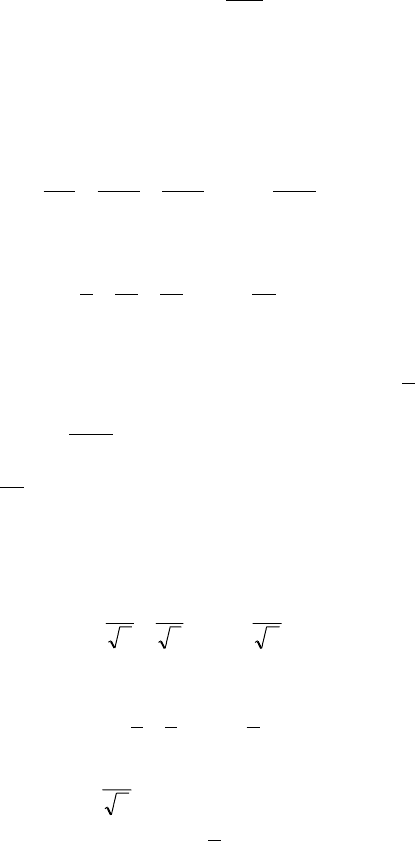
211
Ðåøåíèå. Íàéäåì
.1
1
limlim =
+
=
∞→∞→
n
n
a
n
n
n
Òàêèì îáðàçîì, ïðåäåë îáùåãî ÷ëåíà ðÿäà ïðè n → ∞ îòëè÷åí îò
íóëÿ, ò.å. íåîáõîäèìûé ïðèçíàê ñõîäèìîñòè íå âûïîëíÿåòñÿ. Ýòî
îçíà÷àåò, ÷òî äàííûé ðÿä ðàñõîäèòñÿ.
Ïðèìåð 5.4. Èññëåäîâàòü íà ñõîäèìîñòü ðÿä
. ...
25
1
...
25
1
25
1
25
1
32
+
⋅
++
⋅
+
⋅
+
⋅
n
Ðåøåíèå. Ñðàâíèì äàííûé ðÿä ñ ðÿäîì
. ...
2
1
...
2
1
2
1
2
1
32
+++++
n
(*)
Ðÿä (*) ñõîäèòñÿ, òàê êàê åãî ÷ëåíû îáðàçóþò áåñêîíå÷íî óáûâàþ-
ùóþ ãåîìåòðè÷åñêóþ ïðîãðåññèþ ñî çíàìåíàòåëåì
.
2
1
=q
Ïðè ýòîì
êàæäûé ÷ëåí
n
n
a
25
1
⋅
=
äàííîãî ðÿäà ìåíüøå ñîîòâåòñòâóþùåãî
÷ëåíà
n
n
b
2
1
=
ðÿäà (*). Ïîýòîìó, ñîãëàñíî ïðèçíàêó ñðàâíåíèÿ,
äàííûé ðÿä ñõîäèòñÿ.
Ïðèìåð 5.5. Èññëåäîâàòü íà ñõîäèìîñòü ðÿä
. ...
1
...
3
1
2
1
1
333
+++++
n
Ðåøåíèå. Ñðàâíèì äàííûé ðÿä ñ ãàðìîíè÷åñêèì ðÿäîì
. ...
1
...
3
1
2
1
1 +++++
n
Êàæäûé ÷ëåí
3
1
n
n
a
=
äàííîãî ðÿäà, íà÷èíàÿ ñî âòîðîãî, áîëü-
øå ñîîòâåòñòâóþùåãî ÷ëåíà
n
b
n
1
=
ãàðìîíè÷åñêîãî ðÿäà. Òàê êàê
ãàðìîíè÷åñêèé ðÿä ðàñõîäèòñÿ, òî, ñîãëàñíî ïðèçíàêó ñðàâíåíèÿ,
ðàñõîäèòñÿ è äàííûé ðÿä.

212
Ïðèìåð 5.6. Èññëåäîâàòü íà ñõîäèìîñòü ðÿä
. ...
1
...
3
1
2
1
1
222
+++++
n
Ðåøåíèå. Êàæäûé ÷ëåí ðÿäà
. ...
1
...
3
1
2
1
222
++++
n
(*)
ìåíüøå ñîîòâåòñòâóþùåãî ÷ëåíà ðÿäà
. ...
)1(
1
...
32
1
21
1
+
+
++
⋅
+
⋅ nn
Êàê áûëî ïîêàçàíî â çàäà÷å 5.2, ïîñëåäíèé ðÿä ñõîäèòñÿ. Ñëå-
äîâàòåëüíî, ñõîäèòñÿ è ðÿä (*). Ñõîäèìîñòü èñõîäíîãî ðÿäà, îò-
ëè÷àþùåãîñÿ îò ðÿäà (*) íàëè÷èåì ïåðâîãî ÷ëåíà 1, òåïåðü î÷å-
âèäíà.
Ïðèìåð 5.7. Ñ ïîìîùüþ ïðèçíàêà Äàëàìáåðà ðåøèòü âîïðîñ
î ñõîäèìîñòè ðÿäà
. ...
3
...
3
3
3
2
3
1
32
+++++
n
n
Ðåøåíèå. Äëÿ òîãî ÷òîáû âîñïîëüçîâàòüñÿ ïðèçíàêîì Äàëàì-
áåðà, íàäî çíàòü (n + 1)-é ÷ëåí ðÿäà. Îí ïîëó÷àåòñÿ ïóòåì ïîäñòà-
íîâêè â âûðàæåíèå îáùåãî ÷ëåíà ðÿäà
n
n
n
a
3
=
âìåñòî n ÷èñëà n + 1:
.
3
1
1
1
+
+
+
=
n
n
n
a
Òåïåðü íàéäåì ïðåäåë îòíîøåíèÿ (n + 1)-ãî ÷ëåíà
ê n-ìó ÷ëåíó ïðè n → ∞:
.
3
1
3
1
lim
3
3)1(
lim
3
:
3
1
limlim
11
1
=
+
=
⋅
+
=
+
=
∞→
+
∞→
+
∞→
+
∞→
n
n
n
nnn
a
a
n
n
n
n
nn
n
n
n
n
Òàê êàê
,1
3
1
<=l
òî äàííûé ðÿä ñõîäèòñÿ.
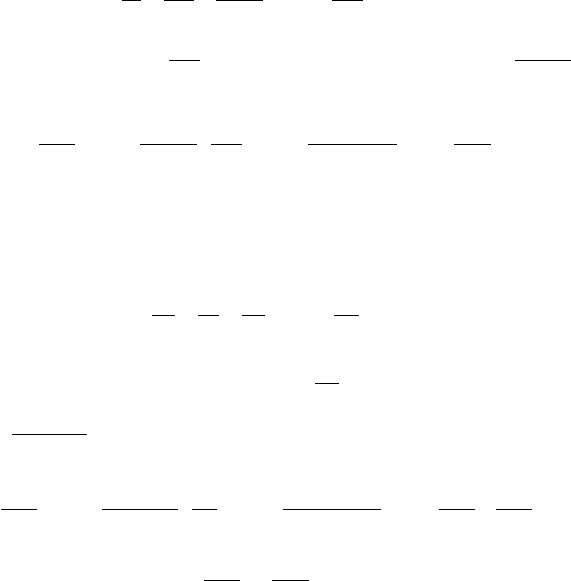
213
Ïðèìåð 5.8. Ïîëüçóÿñü ïðèçíàêîì Äàëàìáåðà, èññëåäîâàòü íà
ñõîäèìîñòü ðÿä
. ...
10
!
...
10
321
10
21
10
1
32
+++
⋅⋅
+
⋅
+
n
n
Ðåøåíèå. Çíàÿ
n
n
n
a
10
!
=
íàéäåì (n + 1)-é ÷ëåí ðÿäà:
.
10
)!1(
1
1
+
+
+
=
n
n
n
à
Âû÷èñëèì
.
10
1
lim
10 !
10)!1(
lim
10
!
:
10
)!1(
limlim
11
1
∞=
+
=
+
=
+
=
∞→
+
∞→
+
∞→
+
∞→
n
n
nnn
a
a
n
n
n
n
nn
n
n
n
n
Òàê êàê l = ∞ > 1, òî ðÿä ðàñõîäèòñÿ.
Ïðèìåð 5.9. Íà îñíîâàíèè ïðèçíàêà Äàëàìáåðà èññëåäîâàòü
ñõîäèìîñòü ðÿäà
. ...
3
...
4
3
3
3
2
3
3
4
4
3
3
2
2
++++++
n
n
n
Ðåøåíèå. Çíàÿ n-é ÷ëåí ðÿäà
n
n
n
n
a
3
=
çàïèøåì (n + 1)-é ÷ëåí:
1
1
1
)1(
3
+
+
+
+
=
n
n
n
n
à
. Îòñþäà
.003
1
1
1
1lim 3
11
3
lim
)1(3
3
lim
3
:
)1(
3
limlim
1
1
1
1
1
1
=⋅⋅=
+
⋅
+
−=
=
+
⋅
+
=
+
⋅
=
+
=
−
∞→
∞→
+
+
∞→
+
+
∞→
+
∞→
e
nn
n
n
n
n
n
n
nn
a
a
n
n
n
n
nn
nn
n
n
n
n
n
n
n
n
n
Òàê êàê l = 0 < 1, òî ðÿä ñõîäèòñÿ.
5.3. Ïðèçíàê ñõîäèìîñòè Ëåéáíèöà
Çíàêî÷åðåäóþùèìñÿ ðÿäîì íàçûâàåòñÿ ðÿä âèäà
à
1
à
2
+ à
3
+ (1)
n1
à
n
+ , (1)
ãäå à
1
, à
2
, à
3,
, à
n
ïîëîæèòåëüíûå ÷èñëà.
Äëÿ çíàêî÷åðåäóþùèõñÿ ðÿäîâ èìååò ìåñòî ñëåäóþùèé ïðè-
çíàê ñõîäèìîñòè.

214
Ïðèçíàê Ëåéáíèöà. Ðÿä (1) ñõîäèòñÿ, åñëè åãî ÷ëåíû ìîíîòîí-
íî óáûâàþò ïî àáñîëþòíîé âåëè÷èíå è îáùèé ÷ëåí ñòðåìèòñÿ ê
íóëþ ïðè n
→ ∞.
Ïðèìåíåíèå ñõîäÿùèõñÿ ðÿäîâ ê ïðèáëèæåííûì âû÷èñëåíè-
ÿì îñíîâàíî íà çàìåíå ñóììû ðÿäà ñóììîé íåñêîëüêèõ ïåðâûõ åãî
÷ëåíîâ. Äîïóñêàåìàÿ ïðè ýòîì ïîãðåøíîñòü î÷åíü ïðîñòî îöåíè-
âàåòñÿ äëÿ çíàêî÷åðåäóþùåãîñÿ ðÿäà, óäîâëåòâîðÿþùåãî ïðèçíà-
êó Ëåéáíèöà, ýòî ïîãðåøíîñòü ìåíüøå àáñîëþòíîãî çíà÷åíèÿ
ïåðâîãî èç îòáðîøåííûõ ÷ëåíîâ ðÿäà.
Ïðèìåð 5.10. Ïîëüçóÿñü ïðèçíàêîì Ëåéáíèöà, èññëåäîâàòü íà
ñõîäèìîñòü çíàêî÷åðåäóþùèéñÿ ðÿä
. ...
1
)1(...
4
1
3
1
2
1
1
1
++++−
n
n
Ðåøåíèå. Òàê êàê ÷ëåíû äàííîãî ðÿäà ïî àáñîëþòíîé âåëè÷è-
íå ìîíîòîííî óáûâàþò:
...
4
1
3
1
2
1
1 >>>>
è îáùèé ÷ëåí ïðè n → ∞ ñòðåìèòñÿ ê íóëþ:
,0lim =
∞→
n
n
a
òî â ñèëó ïðèçíàêà Ëåéáíèöà ðÿä ñõîäèòñÿ.
Ïðèìåð 5.11. Îöåíèòü îøèáêó, äîïóñêàåìóþ ïðè çàìåíå ñóì-
ìû ðÿäà
. ...
1
)1(...
4
1
3
1
2
1
1
1
++++−
n
n
ñóììîé ÷åòûðåõ ïåðâûõ åãî ÷ëåíîâ.
Ðåøåíèå. Äàííûé çíàêî÷åðåäóþùèéñÿ ðÿä ñõîäèòñÿ (ñì. çàäà-
÷ó 5.10). Îøèáêà ∆S
4
, ïîëó÷àþùàÿñÿ ïðè çàìåíå ñóììû S ýòîãî
ðÿäà ñóììîé ÷åòûðåõ ïåðâûõ åãî ÷ëåíîâ, ìåíüøå àáñîëþòíîãî
çíà÷åíèÿ ïÿòîãî ÷ëåíà: ∆S
4
< 0,2.
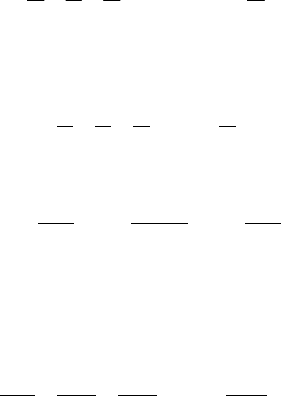
215
5.4. Àáñîëþòíàÿ è óñëîâíàÿ ñõîäèìîñòü
çíàêîïåðåìåííîãî ðÿäà
Ðÿä
à
1
+ à
2
+ + à
n
+ (1)
íàçûâàåòñÿ çíàêîïåðåìåííûì, åñëè ñðåäè åãî ÷ëåíîâ èìåþòñÿ êàê
ïîëîæèòåëüíûå, òàê è îòðèöàòåëüíûå ÷èñëà.
Ïðèçíàê ñõîäèìîñòè çíàêîïåðåìåííîãî ðÿäà. Åñëè ðÿä
| à
1
| + | à
2
| + + | à
n
|
+ , (2)
ñîñòàâëåííûé èç àáñîëþòíûõ âåëè÷èí ÷ëåíîâ ðÿäîâ (1), ñõîäèòñÿ,
òî ðÿä (1) òàêæå ñõîäèòñÿ.
Çíàêîïåðåìåííûé ðÿä (1) íàçûâàåòñÿ àáñîëþòíî ñõîäÿùèìñÿ,
åñëè ñõîäèòñÿ ðÿä (2), ñîñòàâëåííûé èç àáñîëþòíûõ âåëè÷èí ÷ëå-
íîâ äàííîãî ðÿäà (1).
Ñõîäÿùèéñÿ çíàêîïåðåìåííûé ðÿä íàçûâàåòñÿ óñëîâíî ñõîäÿ-
ùèìñÿ, åñëè ðÿä, ñîñòàâëåííûé èç àáñîëþòíûõ âåëè÷èí åãî ÷ëå-
íîâ, ðàñõîäèòñÿ.
Ïðèìåð 5.12. Èññëåäîâàòü íà ñõîäèìîñòü ðÿä
. ...
!
1
)1(...
!4
1
!3
1
!2
1
1
1
++++−
n
n
Ðåøåíèå. Ðàññìîòðèì ðÿä, ñîñòàâëåííûé èç àáñîëþòíûõ âåëè-
÷èí ÷ëåíîâ äàííîãî ðÿäà:
. ...
!
1
...
!4
1
!3
1
!2
1
1 ++++++
n
Ïî ïðèçíàêó Äàëàìáåðà ýòîò ðÿä ñõîäèòñÿ, òàê êàê
.10
1
1
lim
)!1(
!
limlim
1
<=
+
=
+
==
∞→∞→
+
∞→
nn
n
a
a
l
nn
n
n
n
Ñëåäîâàòåëüíî, ïåðâîíà÷àëüíûé ðÿä ÿâëÿåòñÿ àáñîëþòíî ñõî-
äÿùèìñÿ.
Ïðèìåð 5.13. Èññëåäîâàòü íà ñõîäèìîñòü ðÿä
. ...
sin
...
3
3sin
2
2sin
1
1sin
2222
+++++
n
n
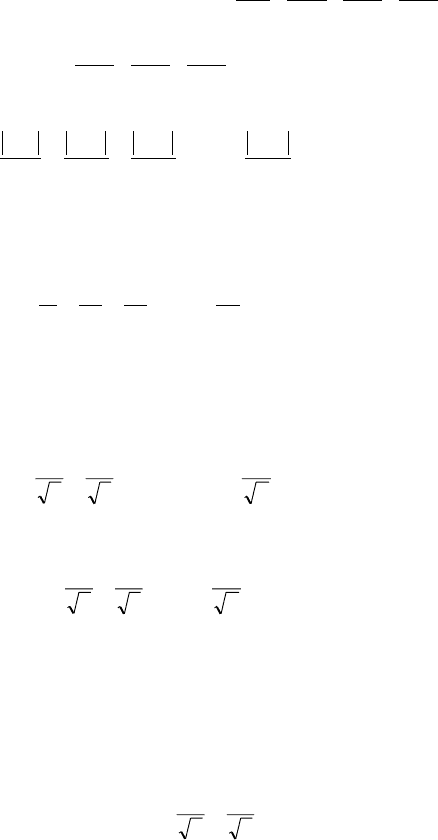
216
Ðåøåíèå. Ðàññìàòðèâàåìûé ðÿä çíàêîïåðåìåííûé, ïîñêîëüêó
îí ñîäåðæèò êàê ïîëîæèòåëüíûå ÷ëåíû
,...,
7
7sin
,
3
3sin
,
2
2sin
,
1
1sin
2222
òàê è îòðèöàòåëüíûå
....,
6
6sin
,
5
5sin
,
4
4sin
222
Ðÿä
...
sin
...
3
3sin
2
2sin
1
1sin
2222
+++++
n
n
ñõîäèòñÿ, òàê êàê åãî ÷ëåíû íå ïðåâîñõîäÿò ñîîòâåòñòâóþùèõ ÷ëå-
íîâ ñõîäÿùåãîñÿ ðÿäà
. ...
1
...
3
1
2
1
1
1
2222
+++++
n
Ñëåäîâàòåëüíî, èñõîäíûé ðÿä ñõîäèòñÿ àáñîëþòíî.
Ïðèìåð 5.14. Èññëåäîâàòü íà ñõîäèìîñòü ðÿä
. ...
1
)1(...
3
1
2
1
1
3
1
33
+⋅++
n
n
(*)
Ðåøåíèå. Ðÿä
, ...
1
...
3
1
2
1
1
333
+++++
n
ñîñòàâëåííûé èç àáñîëþòíûõ âåëè÷èí ÷ëåíîâ äàííîãî ðÿäà, ðàñ-
õîäèòñÿ (ñì. çàäà÷ó 5.5). Ñëåäîâàòåëüíî, ðÿä (*) íå ÿâëÿåòñÿ àáñî-
ëþòíî ñõîäÿùèìñÿ. Îñòàåòñÿ âûÿñíèòü, ñõîäèòñÿ ëè îí (óñëîâíî)
èëè ðàñõîäèòñÿ. Ðàññìàòðèâàåìûé ðÿä çíàêî÷åðåäóþùèéñÿ. Ïî-
ýòîìó äëÿ ðåøåíèÿ âîïðîñà î åãî ñõîäèìîñòè ìîæíî âîñïîëüçî-
âàòüñÿ ïðèçíàêîì Ëåéáíèöà. Òàê êàê ÷ëåíû ðÿäà ïî àáñîëþòíîé
âåëè÷èíå ìîíîòîííî óáûâàþò:
...
3
1
2
1
3
3
1
>>>
è îáùèé ÷ëåí ñòðå-
ìèòñÿ ê íóëþ:
,0lim =
∞→
n
n
a
òî ðÿä (*) ñõîäèòñÿ. Èòàê, äàííûé ðÿä
ñõîäèòñÿ óñëîâíî.

217
Ïðèìåð 5.15. Èññëåäîâàòü íà ñõîäèìîñòü ðÿä
. ...
3
sin...
3
3
sin
3
2
sin
3
sin +++++
ππππ
n
Ðåøåíèå. Äàííûé çíàêîïåðåìåííûé ðÿä ðàñõîäèòñÿ, òàê êàê
äëÿ íåãî íå âûïîëíÿåòñÿ íåîáõîäèìûé ïðèçíàê ñõîäèìîñòè:
3
sinlimlim
π
n
n
n
n
a
∞→∞→
=
íå ñóùåñòâóåò.
5.5. Ñòåïåííûå ðÿäû
Ñòåïåííûì ðÿäîì íàçûâàåòñÿ ðÿä âèäà
à
0
+ à
1
x + à
2
x
2
+ + à
n
x
n
+ , (1)
ãäå à
1
, à
2
, à
3,
, à
n
ïîñòîÿííûå ÷èñëà, íàçûâàåìûå êîýôôè-
öèåíòàìè ðÿäà.
Îáëàñòüþ ñõîäèìîñòè ñòåïåííîãî ðÿäà íàçûâàåòñÿ ñîâîêóï-
íîñòü âñåõ çíà÷åíèé õ, ïðè êîòîðûõ äàííûé ðÿä ñõîäèòñÿ.
Íàõîæäåíèå îáëàñòè ñõîäèìîñòè ñîñòîèò èç äâóõ ýòàïîâ.
1. Îïðåäåëÿåòñÿ èíòåðâàë ñõîäèìîñòè ñòåïåííîãî ðÿäà, ò.å.
èíòåðâàë (R, R) ÷èñëîâîé îñè, ñèììåòðè÷íûé îòíîñèòåëüíî òî÷-
êè õ = 0 è îáëàäàþùèé òåì ñâîéñòâîì, ÷òî ïðè âñåõ | x | < R ðÿä
ñõîäèòñÿ è ïðèòîì àáñîëþòíî, à ïðè âñåõ | x | > R ðÿä ðàñõîäèò-
ñÿ. Äëÿ ýòîãî ïðèìåíÿåòñÿ ïðèçíàê Äàëàìáåðà ê ðÿäó
| à
0
| + | à
1
| | x | + | à
2
| | x |
2
+ + | à
n
| | x |
n
+ ,
÷ëåíû êîòîðîãî åñòü àáñîëþòíûå âåëè÷èíû ÷ëåíîâ äàííîãî ðÿäà (1).
2. Èññëåäóåòñÿ ñõîäèìîñòü ðÿäà (1) íà êîíöàõ èíòåðâàëà ñõî-
äèìîñòè â òî÷êàõ x = R è x = R.
Ïðèìåð 5.16. Èññëåäîâàòü ñõîäèìîñòü ðÿäà
...
2
...
2
4
2
3
2
2
2
1
4
4
3
3
2
2
++++++
n
n
x
n
xxxx
â òî÷êàõ x = 1, x = 3, x = 2.
Ðåøåíèå. Ïðè õ = 1 äàííûé ðÿä ïðåâðàùàåòñÿ â ÷èñëîâîé ðÿä
. ...
2
...
2
3
2
2
2
1
32
+++++
n
n

218
Ïî ïðèçíàêó Äàëàìáåðà ýòîò ðÿä ñõîäèòñÿ, òàê êàê
.1
2
1
2
:
2
1
limlim
1
1
<=
+
==
+
∞→
+
∞→
nn
n
n
n
n
nn
a
a
l
Ïðè õ = 3 èìååì ðÿä
. ...3
2
...3
2
3
3
2
2
3
2
1
3
3
2
2
+⋅++⋅+⋅+⋅
n
n
n
Ïðèìåíÿÿ ïðèçíàê Äàëàìáåðà, ïîëó÷èì
.1
2
3
2
3
:
2
3
)1(limlim
1
1
>=
+==
+
∞→
+
∞→
nn
n
n
n
n
nn
a
a
l
Ñëåäîâàòåëüíî, â òî÷êå õ = 3 äàííûé ðÿä ðàñõîäèòñÿ.
Íàêîíåö, ïðè õ = 2 ïîëó÷àåì ñëåäóþùèé ÷èñëîâîé ðÿä:
1 + 2 3 + 4 ... + (1)
n
n + ... ,
êîòîðûé ðàñõîäèòñÿ (òàê êàê íå âûïîëíÿåòñÿ íåîáõîäèìûé ïðè-
çíàê ñõîäèìîñòè ðÿäà).
Ïðèìåð 5.17. Íàéòè îáëàñòü ñõîäèìîñòè ñòåïåííîãî ðÿäà
. ...
2)1(
)1(...
2423
22
1
3
3
2
2
+
+
−++
⋅
−
⋅
+
⋅
−
n
n
n
n
xxxx
Ðåøåíèå. Ñîñòàâèì ðÿä èç àáñîëþòíûõ âåëè÷èí ÷ëåíîâ äàííî-
ãî ðÿäà:
. ...
2)1(
||
...
24
||
23
||
22
||
1
3
3
2
2
+
+
++
⋅
+
⋅
+
⋅
+
n
n
n
xxxx
Ñîãëàñíî ïðèçíàêó Äàëàìáåðà ïîëó÷åííûé çíàêîïîëîæèòåëü-
íûé ðÿä ñõîäèòñÿ (àáñîëþòíî) ïðè òåõ çíà÷åíèÿõ õ, äëÿ êîòîðûõ
.1lim
1
<=
+
∞→
n
n
n
u
u
l
Çäåñü
,
2)1(
||
n
n
n
n
x
u
+
=
.
2)2(
||
1
1
1
+
+
+
+
=
n
n
n
n
x
u
Îòñþäà
.
2
||
2
1
lim
2
||
2)1(
||
:
2)2(
||
limlim
1
1
1
x
n
nx
n
x
n
x
u
u
l
n
n
n
n
n
n
n
n
n
=
+
+
=
++
==
∞→
+
+
∞→
+
∞→

219
Îïðåäåëèì, ïðè êàêèõ çíà÷åíèÿõ õ ýòîò ïðåäåë l áóäåò ìåíüøå
åäèíèöû. Äëÿ ýòîãî ðåøèì íåðàâåíñòâî
,1
2
||
<
x
èëè | x | < 2, îòêó-
äà 2 < x < 2.
Òàêèì îáðàçîì, ïåðâîíà÷àëüíûé ðÿä ñõîäèòñÿ (àáñîëþòíî) â
èíòåðâàëå (2; 2) ýòî è åñòü èíòåðâàë ñõîäèìîñòè äàííîãî ðÿäà.
Èññëåäóåì ñõîäèìîñòü ðÿäà íà êîíöàõ èíòåðâàëà ñõîäèìîñòè.
Ïðè õ = 2 ïîëó÷àåì ÷èñëîâîé ðÿä
. ...
1
1
...
3
1
2
1
1 +
+
++++
n
Ýòî ãàðìîíè÷åñêèé ðÿä, êîòîðûé, êàê èçâåñòíî, ðàñõîäèòñÿ.
Ïðè õ = 2 ïîëó÷àåì ÷èñëîâîé çíàêî÷åðåäóþùèéñÿ ðÿä
, ...
1
1
)1(...
3
1
2
1
1 +
+
+−+−
n
n
êîòîðûé ïî ïðèçíàêó Ëåéáíèöà ñõîäèòñÿ (óñëîâíî).
Èòàê, îáëàñòü ñõîäèìîñòè äàííîãî ðÿäà 2 < x ≤ 2.
Ïðèìåð 5.18. Íàéòè îáëàñòü ñõîäèìîñòè ñòåïåííîãî ðÿäà
x + 2! x
2
+ 3! x
3
+ + n! x
n
+ .
Ðåøåíèå. Çäåñü u
n
= n! | x |
n
, u
n + 1
= (n + 1)! | x |
n + 1
.
Îòñþäà
),1(lim||
||!
||! )1(
limlim
1
1
+=
+
==
∞→
+
∞→
+
∞→
nx
xn
xn
u
u
l
n
n
n
n
n
n
n
ò.å.
=
≠∞
=
.0ïðè0
,0ïðè
õ
õ
l
Òàêèì îáðàçîì, ñîãëàñíî ïðèçíàêó Äàëàìáåðà ðÿä ñõîäèòñÿ
òîëüêî â òî÷êå õ = 0.
Ïðèìåð 5.19. Íàéòè îáëàñòü ñõîäèìîñòè ñòåïåííîãî ðÿäà
. ...
!
3
...
! 3
3
! 2
3
! 1
3
1
3
3
2
2
++++++
n
n
õ
n
õõõ

220
Ðåøåíèå. Èìååì
.||
! )1(
3
,||
!
3
1
1
1
+
+
+
+
==
n
n
n
n
n
n
xuxu
nn
Îòñþäà
.10
1
3
lim||
||3 ! )1(
||! 3
limlim
11
1
<=
+
=
+
⋅
==
∞→
++
∞→
+
∞→
n
x
xn
xn
u
u
l
n
nn
nn
n
n
n
n
Ñëåäîâàòåëüíî, ïðè ëþáîì êîíå÷íîì õ ïî ïðèçíàêó Äàëàìáåðà
äàííûé ðÿä àáñîëþòíî ñõîäèòñÿ. Îáëàñòü ñõîäèìîñòè ðàññìàòðè-
âàåìîãî ðÿäà åñòü âñÿ ÷èñëîâàÿ îñü.
5.6. Ðàçëîæåíèå ôóíêöèé
â ñòåïåííûå ðÿäû Òåéëîðà
Ðÿäîì Òåéëîðà äëÿ ôóíêöèè f (x) íàçûâàåòñÿ ñòåïåííîé ðÿä
âèäà
. ...
!
)0(
...
! 3
)0(
! 2
)0(
)0()0()(
)(
32
+++
′′′
+
′′
+
′
+=
n
n
x
n
f
x
f
x
f
x
f
f
x
f
(1)
Ïðè ïðåäñòàâëåíèè ýëåìåíòàðíîé ôóíêöèè â âèäå ñóììû ðÿäà
Òåéëîðà îáû÷íî ïîñòóïàþò ñëåäóþùèì îáðàçîì: âû÷èñëÿþò ïîñ-
ëåäîâàòåëüíûå ïðîèçâîäíûå äàííîé ôóíêöèè â òî÷êå õ = 0, à çà-
òåì, ïîëüçóÿñü ôîðìóëîé (1), ñîñòàâëÿþò äëÿ íåå ðÿä Òåéëîðà è
îïðåäåëÿþò èíòåðâàë ñõîäèìîñòè ïîëó÷åííîãî ðÿäà.  ýòîì èí-
òåðâàëå ðÿä Òåéëîðà ñõîäèòñÿ ê ïîðîäèâøåé åãî ôóíêöèè f (x),
åñëè òîëüêî âñå çíà÷åíèÿ f (0), f ′ (0), , f
(n)
(0), ïîëó÷àþòñÿ
íåïîñðåäñòâåííîé ïîäñòàíîâêîé çíà÷åíèÿ õ = 0 â âûðàæåíèÿ f (õ),
f ′ (õ), , f
(n)
(õ), .
Ïðèìåíÿÿ ðàññìîòðåííûé ñïîñîá, ìîæíî íàéòè ðàçëîæåíèå â
ðÿä Òåéëîðà äëÿ ñëåäóþùèõ ôóíêöèé:
),( ...
!
...
! 3! 2
1
32
∞<<∞++++++= x
n
xxx
xå
n
x
(2)
),( ...
! )12(
)1(...
! 5! 3
sin
1253
∞<<∞+
+
+−+−=
+
x
n
xxx
xx
n
n
(3)
),( ...
! )2(
)1(...
! 4! 2
1cos
242
∞<<∞++−+−= x
n
xxx
x
n
n
(4)
