Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
Подождите немного. Документ загружается.


191
Òîãäà
dx
dv
u
dx
du
dx
dy
+=
υ
è óðàâíåíèå (1) ïðèíèìàåò âèä
)()( xQxP
dx
dv
u
dx
du
=
++
υυ
(2)
Ïîëüçóÿñü òåì, ÷òî îäíî èç âñïîìîãàòåëüíûõ ïåðåìåííûõ, íà-
ïðèìåð
υ
, âûáðàíî ïðîèçâîëüíî, ïîäáåðåì åãî òàê, ÷òîáû âûðà-
æåíèå â êâàäðàòíûõ ñêîáêàõ îáðàòèëîñü â íóëü, ò.å. â êà÷åñòâå
υ
âîçüìåì îäíî èç ÷àñòíûõ ðåøåíèé
υ
=
υ
(õ) óðàâíåíèÿ ñ ðàçäåëÿþ-
ùèìèñÿ ïåðåìåííûìè
.0)( =+
υ
xP
dx
dv
Ïîäñòàâèâ âûðàæåíèå
υ
=
υ
(õ) â óðàâíåíèå (2), ïîëó÷èì óðàâ-
íåíèå îòíîñèòåëüíî ôóíêöèè u:
).(xQ
dx
du
=
υ
Ýòî òàêæå óðàâíåíèå ñ ðàçäåëÿþùèìèñÿ ïåðåìåííûìè. Íàéäÿ
îáùåå ðåøåíèå ýòîãî óðàâíåíèÿ u = u(õ, C), ïîëó÷èì îáùåå ðåøå-
íèå óðàâíåíèÿ (1):
y = u(õ, C)
υ
(x).
Ïðèìåð 4.9. Íàéòè îáùåå ðåøåíèå óðàâíåíèÿ
y′ y tg x = sin x.
Ðåøåíèå. Ïîëîæèì y = u
υ
, òîãäà y′ = u′
υ
+ u
υ
′ è äàííîå óðàâíå-
íèå ïðèíèìàåò âèä
u′
υ
+ u
υ
′ u
υ
tg x = sin x,
èëè
u′
υ
+ u(
υ
′
υ
tg x) = sin x. (*)
Ðåøàÿ óðàâíåíèå
υ
′
υ
tg x = 0, ïîëó÷èì ïðîñòåéøåå ÷àñòíîå
ðåøåíèå:
,|cos|ln||ln;tg;tg xdxx
d
x
dx
d
−===
υ
υ
υ
υ
υ
îòêóäà
.
cos
1
x
=
υ
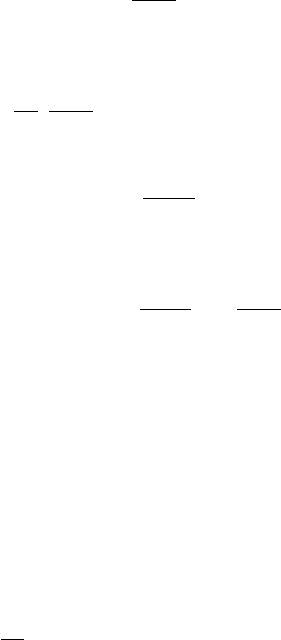
192
Ïîäñòàâëÿÿ
υ
â óðàâíåíèå (*), ïîëó÷èì óðàâíåíèå
x
x
u sin
cos
1
=⋅
′
èç êîòîðîãî íàõîäèì u:
,cossin;sin
cos
1
dxxxdux
xdx
du
==⋅
îòêóäà
.
2
sin
2
C
x
u +=
Èòàê, èñêîìîå îáùåå ðåøåíèå
.
cos
1
2
sin
2
x
C
x
uy
+==
υ
Ïðèìåð 4.10. Ðåøèòü äèôôåðåíöèàëüíîå óðàâíåíèå:
y′ + y · tg x = cos
2
x.
Ðåøåíèå. Ïîëàãàÿ y = u
υ
, ïðèâîäèì ýòî óðàâíåíèå ê âèäó
υ
[u′ + u tg x] + u
υ
′= cos
2
x.
Ïðèðàâíÿåì êâàäðàòíóþ ñêîáêó ê íóëþ:
u′ + u tg x = 0,
ìû ïîëó÷èì, ÷òî
.cos,coslnln;tg xuxudxx
u
du
==−=
Ïîäñòàâëÿÿ ïîëó÷åííîå çíà÷åíèå u â óðàâíåíèå, ïîëó÷àåì ñëå-
äóþùåå óðàâíåíèå äëÿ
υ
:
ños x ·
υ
′ = cos
2
x.
Îòñþäà íàõîäèì:
υ
′ = cos
x,
υ
= sin x + C.
Òàêèì îáðàçîì,
y = u
υ
= cos x(sin x + C).
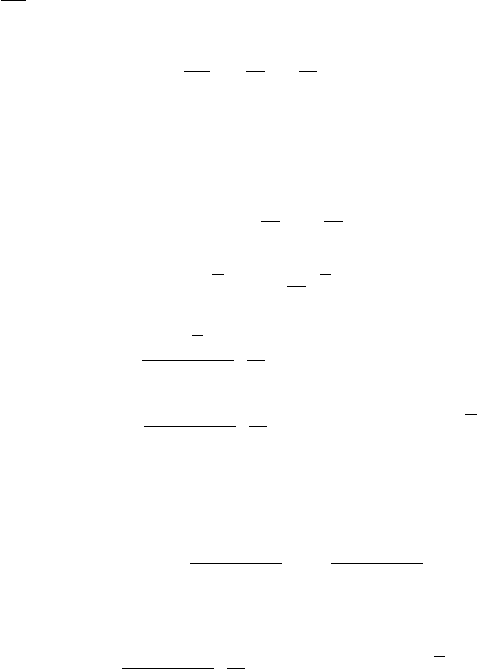
193
Ïðèìåð 4.11. Ðàññìîòðèì ñëåäóþùóþ çàäà÷ó:
Ìàòåðèàëüíàÿ òî÷êà äâèæåòñÿ ïî ïðÿìîé ëèíèè â ñîïðîòèâ-
ëÿþùåéñÿ ñðåäå ïîä äåéñòâèåì ïåðèîäè÷åñêè ìåíÿþùåéñÿ ñèëû
F
1
= A sin
ω
t. Ñîïðîòèâëåíèå ñðåäû ïðîïîðöèîíàëüíî ñêîðîñòè
äâèæåíèÿ. Âûâåñòè çàêîí èçìåíåíèÿ ñêîðîñòè òåëà, åñëè åãî íà-
÷àëüíàÿ ñêîðîñòü ðàâíÿëàñü íóëþ.
Ïî óñëîâèþ íà òåëî äåéñòâóþò äâå ñèëû: ñèëà ñîïðîòèâëåíèÿ
ñðåäû F
2
= k
υ
è ïåðèîäè÷åñêàÿ ñèëà F
1
= A sin
ω
t. Îáùàÿ ñèëà
ðàâíà F = k
υ
+ A sin
ω
t. Íî ïî âòîðîìó çàêîíó Íüþòîíà èìååì
F = ma, à óñêîðåíèå ýòî ïðîèçâîäíàÿ ñêîðîñòè ïî âðåìåíè:
.
dt
d
a
υ
=
Îòñþäà ïðèõîäèì ê óðàâíåíèþ
.sin t
m
A
m
k
dt
d
ωυ
υ
+−=
Ýòî ëèíåéíîå óðàâíåíèå ïåðâîãî ïîðÿäêà. Ïîëàãàÿ
υ
= uw, íà-
õîäèì, ÷òî
.cossin
;cossin
;sin;
;sin
222
222
t
t
tt
m
k
m
k
m
k
m
k
Cett
m
k
mk
A
uw
Ctt
m
k
mk
Ae
w
te
m
A
weu
t
m
A
u
m
k
uwwu
−
−
+
−
+
==
+
−
+
=
=
′
=
=
+
′
+
′
ωωω
ω
υ
ωωω
ω
ω
ω
Ïîëàãàÿ t = 0,
υ
= 0, íàõîäèì
;,0
222222
ω
ω
ω
ω
mk
A
C
mk
A
C
+
=
+
−=
èìååì
.cossin
222
+−
+
=
−
t
m
k
ått
m
k
mk
A
ωωωω
ω
υ
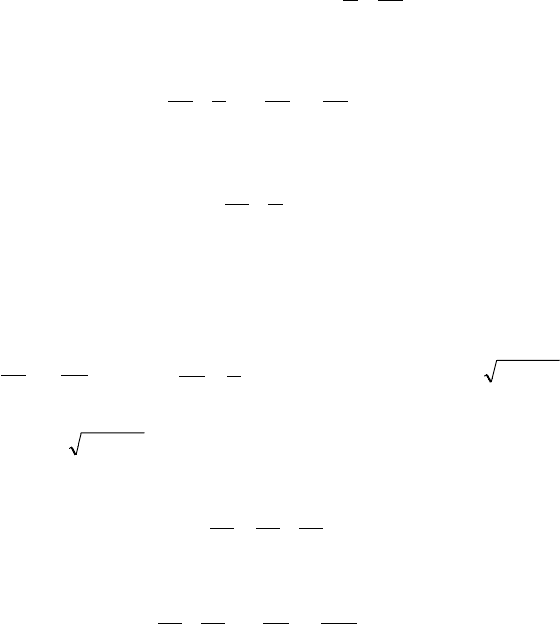
194
4.5. Óðàâíåíèå Áåðíóëëè
Óðàâíåíèåì Áåðíóëëè íàçûâàåòñÿ äèôôåðåíöèàëüíîå óðàâíå-
íèå 1-ãî ïîðÿäêà âèäà:
y = P(x)y + Q(x)y
m
,
ãäå m ≠ 0, m ≠ 1 (ïðè m = 0 óðàâíåíèå ÿâëÿåòñÿ ëèíåéíûì, à ïðè
m = 1 óðàâíåíèå ñ ðàçäåëÿþùèìèñÿ ïåðåìåííûìè).
Òàê æå, êàê è ëèíåéíîå, óðàâíåíèå Áåðíóëëè ìîæíî ïðîèíòåã-
ðèðîâàòü ñ ïîìîùüþ ïîäñòàíîâêè y = u
υ
èëè ñâåñòè ê ëèíåéíîìó
óðàâíåíèþ ñ ïîìîùüþ ïîäñòàíîâêè z = y
1 m
.
Ïðèìåð 4.12. Ðåøèòü óðàâíåíèå
.
2
y
x
x
y
y
+
=
′
Ïîëàãàÿ y = u
υ
, ïðèâîäèì óðàâíåíèå ê âèäó
.0
2
=
−+
−
υ
υ
υ
u
x
u
dx
d
x
u
dx
du
Èç îáùåãî ðåøåíèÿ u = Cx óðàâíåíèÿ
0=−
x
u
dx
du
âûáèðàåì â êà÷åñòâå ôóíêöèè u îäíî ÷àñòíîå ðåøåíèå, íàïðèìåð
u
1
= õ.
Ïîäñòàâëÿÿ u
1
â èñõîäíîå óðàâíåíèå, ïîëó÷àåì íîâîå óðàâíå-
íèå
,0
2
=−
υ
υ
x
x
dx
d
x
èëè
.
1
υ
υ
=
dx
d
Åãî îáùåå ðåøåíèå
.2 Cx +=
υ
Ïåðåìíîæàÿ u
1
è v, ïîëó÷àåì îáùåå ðåøåíèå èñõîäíîãî óðàâ-
íåíèÿ
.2 Cxxy +=
Ïðèìåð 4.13. Ðåøèòü óðàâíåíèå Áåðíóëëè îòíîñèòåëüíî x = x (y):
.
2
1
2 xy
x
dy
dx
−=
Ïîëîæèì x = u
υ
è ïðèâåäåì óðàâíåíèå ê âèäó:
.0
2
1
2
=
++
−
υ
υ
υ
u
u
dy
d
y
u
dy
du

195
Ðàññìîòðåâ óðàâíåíèå
,0
2
=−
y
u
dy
du
âîçüìåì åãî ÷àñòíîå ðåøåíèå
.
1
yu =
Òîãäà ìû ïðèäåì ê óðàâíå-
íèþ
,0
2
1
=
+
y
dy
d
y
υ
υ
îáùåå ðåøåíèå êîòîðîãî
.ln
2
y
C
=
υ
Ïåðåìíîæàÿ yu =
2
1
è
υ
2
, ïîëó÷èì îáùèé èíòåãðàë èñõîäíîãî
óðàâíåíèÿ
.ln
2
y
C
yx =
4.6. Äèôôåðåíöèàëüíûå óðàâíåíèÿ
âòîðîãî ïîðÿäêà âèäà y
″″
″″
″ = f (x)
Óðàâíåíèÿ âèäà y″ = f (x) ðåøàþòñÿ äâóêðàòíûì èíòåãðèðîâà-
íèåì. Ïîëàãàÿ y′ = z, ïîëó÷èì y″ = z′; â ðåçóëüòàòå ïðèõîäèì ê
óðàâíåíèþ ïåðâîãî ïîðÿäêà ñ ðàçäåëÿþùèìèñÿ ïåðåìåííûìè:
),(xfz =
′
èëè
),(xf
dx
dz
=
èëè dz = f (x)dx.
Èíòåãðèðóÿ ýòî óðàâíåíèå, ïîëó÷èì
∫∫
=
,)(dxxfdz
îòêóäà
z = F (x) + C
1
[çäåñü F (x) ïåðâîîáðàçíàÿ îò f (x)]. Çàìåíÿåì â ïîñëåäíåì óðàâ-
íåíèè z çíà÷åíèåì
:
dx
dy
,)(
1
CxF
dx
dy
+=
èëè
dy = [F (x) + C
1
]dx.
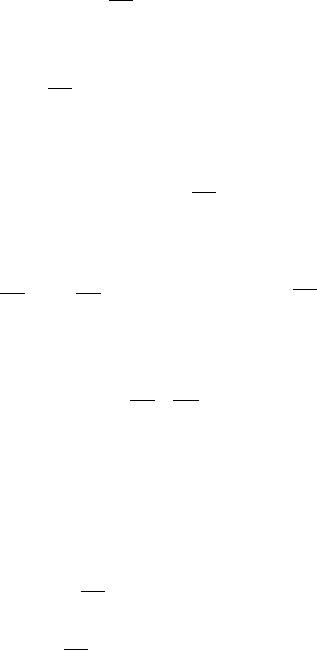
196
Èíòåãðèðóÿ ïîñëåäíåå óðàâíåíèå, íàõîäèì
,)(
21
CxCdxxFy ++=
∫
îòêóäà
ó = Φ(õ) + Ñ
1
õ + Ñ
2
.
Ýòî è åñòü îáùåå ðåøåíèå óðàâíåíèÿ y″ = f (x).
Ïðèìåð 4.14. Íàéòè îáùåå ðåøåíèå óðàâíåíèÿ
y″ = 1 x
2
.
Ðåøåíèå. Ïîëîæèì
,z
dx
d
y
=
òîãäà äàííîå óðàâíåíèå çàïèøåòñÿ
â âèäå:
,1
2
x
dx
dz
=
èëè dz = (1 x
2
)dx.
 ðåçóëüòàòå èíòåãðèðîâàíèÿ íàéäåì
.
3
1
3
C
x
xz +−=
Îòñþäà
,
3
1
3
C
x
x
dx
dy
+−=
èëè
.
3
1
3
dxC
x
xdy
+−=
Èíòåãðèðóÿ ýòî óðàâíåíèå, ïîëó÷àåì îáùåå ðåøåíèå
.
122
21
42
CxC
xx
y ++−=
Ïðèìåð 4.15. Íàéòè ÷àñòíîå ðåøåíèå óðàâíåíèÿ
y″ = sin x
1,
óäîâëåòâîðÿþùåå çàäàííûì íà÷àëüíûì óñëîâèÿì y (0) = 1,
y′ (0) = 1.
Ðåøåíèå. Èìååì
,
z
dx
d
y
=
îòêóäà
;)1(sin,1sin dxxdzx
dx
dz
−==
z = cos x x + C
1
.
197
Ñëåäîâàòåëüíî,
y′ = cos x x + C
1
.
Èñïîëüçóÿ íà÷àëüíûå óñëîâèÿ y′ (0) = 1, ïîëó÷àåì
1 = cos 0 + C
1
,
îòêóäà C
1
= 2. Òàêèì îáðàçîì,
,2cos +−= xx
dx
dy
èëè
dy = (cos x x + 2)dx.
Èíòåãðèðóåì ýòî óðàâíåíèå:
.2
2
sin
2
2
Cx
x
xy ++−−=
Èñïîëüçóÿ òåïåðü íà÷àëüíûå óñëîâèÿ y (0) = 1, íàõîäèì
C
2
= 1. Èòàê, èñêîìîå ÷àñòíîå ðåøåíèå èìååò âèä:
.12
2
sin
2
−+−−= x
x
xy
4.7. Ëèíåéíûå îäíîðîäíûå äèôôåðåíöèàëüíûå
óðàâíåíèÿ âòîðîãî ïîðÿäêà ñ ïîñòîÿííûìè
êîýôôèöèåíòàìè
Ëèíåéíûì îäíîðîäíûì äèôôåðåíöèàëüíûì óðàâíåíèåì âòî-
ðîãî ïîðÿäêà ñ ïîñòîÿííûìè êîýôôèöèåíòàìè íàçûâàåòñÿ óðàâ-
íåíèå âèäà
y″ + py′ + qy = 0. (1)
Äëÿ îòûñêàíèÿ îáùåãî ðåøåíèÿ óðàâíåíèÿ (1) ñîñòàâëÿåòñÿ
õàðàêòåðèñòè÷åñêîå óðàâíåíèå
r
2
+ pr + q = 0, (2)
êîòîðîå ïîëó÷àåòñÿ èç óðàâíåíèÿ (1) çàìåíîé â íåì ïðîèçâîäíûõ
èñêîìîé ôóíêöèè ñîîòâåòñòâóþùèìè ñòåïåíÿìè r, ïðè÷åì ñàìà
ôóíêöèÿ çàìåíÿåòñÿ åäèíèöåé.
198
Òîãäà îáùåå ðåøåíèå óðàâíåíèÿ (1) ñòðîèòñÿ â çàâèñèìîñòè
îò õàðàêòåðà êîðíåé r
1
è r
2
óðàâíåíèÿ (2). Çäåñü âîçìîæíû òðè
ñëó÷àÿ.
1-é ñëó÷àé. Êîðíè r
1
è r
2
äåéñòâèòåëüíûå è ðàçëè÷íûå.
Òîãäà îáùåå ðåøåíèå óðàâíåíèÿ (1) èìååò âèä:
.
2
1
11
xr
xr
eCeCy
+=
(3)
2-é ñëó÷àé. Êîðíè r
1
è r
2
äåéñòâèòåëüíûå è ðàâíûå:
r
1
= r
2
= r.  ýòîì ñëó÷àå îáùåå ðåøåíèå óðàâíåíèÿ (1) èìååò âèä:
ó = (Ñ
1
+ Ñ
2
x)e
rx
. (4)
3-é ñëó÷àé. Êîðíè r
1
è r
2
êîìïëåêñíî ñîïðÿæåííûå:
r
1
=
α
+
β
i, r
2
=
α
β
i. Òîãäà îáùåå ðåøåíèå çàâèñûâàåòñÿ òàê:
ó = e
ax
(Ñ
1
cos
β
x + Ñ
2
sin
β
x). (5)
Ïðèìåð 4.16. Íàéòè îáùåå ðåøåíèå óðàâíåíèÿ
y″ 5y′ 6y = 0.
Ðåøåíèå. Çàïèøåì õàðàêòåðèñòè÷åñêîå óðàâíåíèå; äëÿ ýòîãî
çàìåíèì ôóíêöèþ ó è åå ïðîèçâîäíûå y′ è y″ ñîîòâåòñòâóþùèìè
ñòåïåíÿìè r: r
0
= 1, r è r
2
. Òîãäà ïîëó÷èì
r
2
5r 6 = 0,
îòêóäà r
1
= 1, r
2
= 6. Òàê êàê êîðíè õàðàêòåðèñòè÷åñêîãî
óðàâíåíèÿ äåéñòâèòåëüíûå è ðàçëè÷íûå, òî îáùåå ðåøåíèå äàí-
íîãî äèôôåðåíöèàëüíîãî óðàâíåíèÿ ñîãëàñíî ôîðìóëå (3) èìååò
âèä:
ó = Ñ
1
e
x
+ Ñ
2
e
6x
.
Ïðèìåð 4.17. Íàéòè îáùåå ðåøåíèå óðàâíåíèÿ
y″ 4y′ + 4y = 0.
Ðåøåíèå. Ñîñòàâëÿåì õàðàêòåðèñòè÷åñêîå óðàâíåíèå
r
2
4r + 4 = 0,
199
èç êîòîðîãî íàõîäèì r
1,2
= 2. Õàðàêòåðèñòè÷åñêîå óðàâíåíèå èìå-
åò ðàâíûå äåéñòâèòåëüíûå êîðíè, ïîýòîìó ñîãëàñíî ôîðìóëå (4)
îáùåå ðåøåíèå çàïèøåòñÿ ñëåäóþùèì îáðàçîì:
ó = e
2x
(Ñ
1
+ Ñ
2
x).
Ïðèìåð 4.18. Íàéòè îáùåå ðåøåíèå óðàâíåíèÿ
y″ + 9y = 0.
Ðåøåíèå. Ýòîìó óðàâíåíèþ ñîîòâåòñòâóåò õàðàêòåðèñòè÷åñêîå
óðàâíåíèå
r
2
+ 9 = 0,
èìåþùåå äâà ìíèìûõ ñîïðÿæåííûõ êîðíÿ r
1,2
= ±3i. Èñïîëüçóÿ
ôîðìóëó (5) ïðè
α
= 0 è
β
= 3, ïîëó÷àåì îáùåå ðåøåíèå
ó = Ñ
1
cos 3x + Ñ
2
sin 3x.
Ïðèìåð 4.19. Íàéòè îáùåå ðåøåíèå óðàâíåíèÿ
y″ + 6y′ + 25y = 0.
Ðåøåíèå. Õàðàêòåðèñòè÷åñêîå óðàâíåíèå
r
2
+ 6r + 25 = 0
èìååò äâà êîìïëåêñíî ñîïðÿæåííûõ êîðíÿ r
1,2
= 3 ± 4i. Ïî ôîð-
ìóëå (5) ïðè
α
= 3 è
β
= 4, ïîëó÷àåì îáùåå ðåøåíèå
ó = e
3x
(Ñ
1
cos 4x + Ñ
2
sin 4x).
Ïðèìåð 4.20. Íàéòè ÷àñòíîå ðåøåíèå óðàâíåíèÿ y″ 3y′ + 2y = 0,
óäîâëåòâîðÿþùåå çàäàííûì íà÷àëüíûì óñëîâèÿì y(0) = 1,
y′ (0) = 1.
Ðåøåíèå. Çàïèøåì õàðàêòåðèñòè÷åñêîå óðàâíåíèå
r
2
3r + 2 = 0
åãî êîðíè r
1
= 1, r
2
= 2. Ñëåäîâàòåëüíî, îáùåå ðåøåíèå èìååò
âèä:
ó = Ñ
1
e
x
+ Ñ
2
e
2x
.
200
Äàëåå, èñïîëüçóÿ íà÷àëüíûå óñëîâèÿ, îïðåäåëÿåì çíà÷åíèÿ
ïîñòîÿííûõ Ñ
1
è Ñ
2
. Äëÿ ýòîãî ïîäñòàâèì â îáùåå ðåøåíèå çàäàí-
íûå çíà÷åíèÿ õ = 0, ó = 1; â ðåçóëüòàòå ïîëó÷èì îäíî èç óðàâíå-
íèé, ñâÿçûâàþùåå Ñ
1
è Ñ
2
:
1 = Ñ
1
+ Ñ
2
.
Âòîðîå óðàâíåíèå îòíîñèòåëüíî Ñ
1
è Ñ
2
ïîëó÷èì ñëåäóþùèì
îáðàçîì. Ïðîäèôôåðåíöèðóåì îáùåå ðåøåíèå:
ó′ = Ñ
1
e
x
+ 2Ñ
2
e
2x
è ïîäñòàâèì â íàéäåííîå âûðàæåíèå çàäàííû å çíà÷åíèÿ õ = 0,
ó′ = 1:
1 = Ñ
1
+ 2Ñ
2
.
Èç ñèñòåìû
=+
=+
12
,1
21
21
CC
CC
íàõîäèì Ñ
1
= 3, Ñ
2
= 2. Ñëåäîâàòåëüíî, èñêîìîå ÷àñòíîå ðåøå-
íèå èìååò âèä
ó = 3e
x
2e
2x
.
4.8. Ëèíåéíûå íåîäíîðîäíûå äèôôåðåíöèàëüíûå
óðàâíåíèÿ âòîðîãî ïîðÿäêà ñ ïîñòîÿííûìè
êîýôôèöèåíòàìè
Ëèíåéíîå íåîäíîðîäíîå äèôôåðåíöèàëüíîå óðàâíåíèå âòîðî-
ãî ïîðÿäêà ñ ïîñòîÿííûìè êîýôôèöèåíòàìè èìååò âèä:
y″ + py′ + qy= f (x). (1)
Îíî îòëè÷àåòñÿ îò ñîîòâåòñòâóþùåãî ëèíåéíîãî îäíîðîäíî-
ãî óðàâíåíèÿ
y″ + py′ + qy = 0. (2)
íàëè÷èåì â ïðàâîé ÷àñòè íåêîòîðîé ôóíêöèè f (x).
