Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
Подождите немного. Документ загружается.

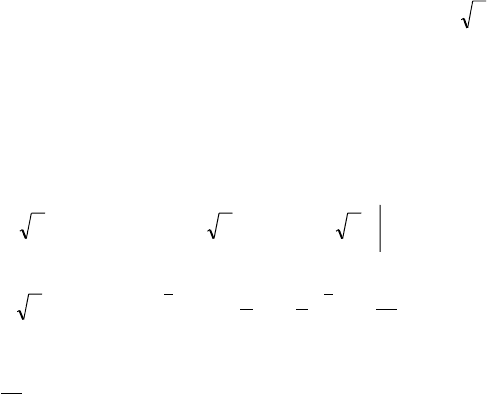
181
ñ ïëîñêîñòüþ xOy (z = 0) ïëîñêîñòåé x = 0, y = x è
yyz −=1
(ðèñ. 51 á). Âåðøèíàìè ýòîãî òðåóãîëüíèêà ÿâëÿþòñÿ òî÷êè (0; 0),
(0; 1), (1; 1), ïîëó÷àþùèåñÿ â ðåçóëüòàòå ðåøåíèÿ ñèñòåì óðàâíå-
íèé, ñîñòàâëåííûõ èç ñîîòâåòñòâóþùèõ ïàð óðàâíåíèé ñòîðîí. Ýòó
îáëàñòü ìîæíî ðàññìàòðèâàòü êàê çàêëþ÷åííóþ â ïîëîñå ìåæäó
ïðÿìûìè y = 0 è y= 1; ñëåâà îáëàñòü îãðàíè÷åíà ïðÿìîé x = 0, à
ñïðàâà ïðÿìîé x = y. Ñëåäîâàòåëüíî,
() ()()
()
∫∫
∫∫∫∫∫
=
−=
−=−=
=−=−=−=
1
0
1
0
2
7
2
1
0
2
5
1
00
1
0
.
14
3
7
2
2
1
1
0
111
yydyyyydyyy
dy
y
xyydxyydydydxyyV
y
D
Èòàê,
14
3
=V
êóá. åä.

182
Ðàçäåë 4
ÄÈÔÔÅÐÅÍÖÈÀËÜÍÛÅ ÓÐÀÂÍÅÍÈß
4.1. Îñíîâíûå ïîíÿòèÿ
Óðàâíåíèå, ñâÿçûâàþùåå íåçàâèñèìóþ ïåðåìåííóþ, íåèçâåñò-
íóþ ôóíêöèþ è åå ïðîèçâîäíûå èëè äèôôåðåíöèàëû ðàçëè÷íûõ
ïîðÿäêîâ, íàçûâàåòñÿ äèôôåðåíöèàëüíûì óðàâíåíèåì.
Ïîðÿäêîì äèôôåðåíöèàëüíîãî óðàâíåíèÿ íàçûâàåòñÿ ïîðÿäîê
ñòàðøåé ïðîèçâîäíîé, âõîäÿùåé â ýòî óðàâíåíèå. Íàïðèìåð, óðàâ-
íåíèå y′ sin x + y tg x = 1 ïåðâîãî ïîðÿäêà;
3
2
2
x
dx
y
d
=
âòîðîãî
ïîðÿäêà; y″′ 5õy′ + õó = 0 òðåòüåãî ïîðÿäêà.
Ôóíêöèÿ y =
ϕ
(x), óäîâëåòâîðÿþùàÿ äèôôåðåíöèàëüíîìó
óðàâíåíèþ, íàçûâàåòñÿ ðåøåíèåì ýòîãî óðàâíåíèÿ. Ãðàôèê ðåøå-
íèÿ íàçûâàåòñÿ èíòåãðàëüíîé êðèâîé óðàâíåíèÿ.
Åñëè ôóíêöèÿ, óäîâëåòâîðÿþùàÿ äèôôåðåíöèàëüíîìó óðàâíå-
íèþ, çàäàíà íåÿâíî, ò.å. ñîîòíîøåíèåì âèäà
ϕ
(x, ó) = 0, òî ãîâî-
ðÿò îá èíòåãðàëå óðàâíåíèÿ.
Ðåøåíèå äèôôåðåíöèàëüíîãî óðàâíåíèÿ, ñîäåðæàùåå ñòîëüêî
íåçàâèñèìûõ ïðîèçâîëüíûõ ïîñòîÿííûõ, êàêîâ ïîðÿäîê óðàâíå-
íèÿ, íàçûâàåòñÿ îáùèì ðåøåíèåì ýòîãî óðàâíåíèÿ. Òàê, äëÿ óðàâ-
íåíèÿ ïåðâîãî ïîðÿäêà îáùåå ðåøåíèå èìååò âèä:
y =
ϕ
(x, Ñ),
à äëÿ óðàâíåíèÿ âòîðîãî ïîðÿäêà âèä:
y =
ϕ
(x, Ñ
1
, Ñ
2
).
Ôóíêöèè, ïîëó÷àåìûå èç îáùåãî ðåøåíèÿ ïðè ðàçëè÷íûõ ÷èñ-
ëîâûõ çíà÷åíèÿõ ïðîèçâîëüíûõ ïîñòîÿííûõ, íàçûâàþòñÿ ÷àñòíû-
ìè ðåøåíèÿìè ýòîãî óðàâíåíèÿ.
Ãåîìåòðè÷åñêè îáùåå ðåøåíèå îïðåäåëÿåò ñåìåéñòâî êðèâûõ,
à ÷àñòíîå ðåøåíèå íåêîòîðóþ êðèâóþ ýòîãî ñåìåéñòâà.
Äëÿ íàõîæäåíèÿ ÷àñòíîãî ðåøåíèÿ äèôôåðåíöèàëüíîãî óðàâ-
íåíèÿ çàäàþòñÿ íà÷àëüíûå óñëîâèÿ. Äëÿ óðàâíåíèÿ ïåðâîãî ïî-

183
ðÿäêà îíè èìåþò âèä y(x
0
) = y
0
; äëÿ óðàâíåíèÿ âòîðîãî ïîðÿäêà
âèä y(x
0
) = y
0
, y′(x
0
) = y′
0
. Ïî ýòèì íà÷àëüíûì óñëîâèÿì îïðåäåëÿ-
þòñÿ çíà÷åíèÿ ïðîèçâîëüíûõ ïîñòîÿííûõ â îáùåì ðåøåíèè óðàâ-
íåíèÿ, â ðåçóëüòàòå ÷åãî ïîëó÷àþòñÿ ÷àñòíûå ðåøåíèÿ, óäîâëåò-
âîðÿþùèå çàäàííûì íà÷àëüíûì óñëîâèÿì.
Ïðèìåð 4.1. Ïðîâåðèòü, ÷òî ôóíêöèÿ y = cos x ÿâëÿåòñÿ ðåøå-
íèåì óðàâíåíèÿ y″ + y = 0.
Ðåøåíèå. Èìååì
y′ = sin x, y″ = cos x.
Ïîäñòàâëÿÿ âûðàæåíèÿ äëÿ y″ è y â äàííîå óðàâíåíèå, ïî-
ëó÷àåì:
y″ + y = cos x + cos x = 0,
ò.å., äåéñòâèòåëüíî, ôóíêöèÿ y = cos x ÿâëÿåòñÿ ðåøåíèåì äàííîãî
äèôôåðåíöèàëüíîãî óðàâíåíèÿ.
Ïðèìåð 4.2. Ïîêàçàòü, ÷òî ôóíêöèÿ y, îïðåäåëÿåìàÿ óðàâíåíè-
åì x
2
y
2
= 4, ÿâëÿåòñÿ èíòåãðàëîì äèôôåðåíöèàëüíîãî óðàâíå-
íèÿ
.
y
x
y
=
′
Ðåøåíèå. Ïðîäèôôåðåíöèðîâàâ îáå ÷àñòè ðàâåíñòâà ïî ïåðå-
ìåííîé õ, ïîëó÷èì:
2õ 2óó′ = 0,
îòêóäà
.
y
x
y
=
′
4.2. Óðàâíåíèÿ ñ ðàçäåëÿþùèìèñÿ ïåðåìåííûìè
Äèôôåðåíöèàëüíîå óðàâíåíèå ñ ðàçäåëÿþùèìèñÿ ïåðåìåííû-
ìè èìååò âèä:
M
1
(x) N
1
(y)dx + M
2
(x) N
2
(y)dy = 0.
Ðåøàåòñÿ îíî ñëåäóþùèì îáðàçîì. Ïîäåëèâ âñå ÷ëåíû óðàâ-
íåíèÿ íà N
1
(y) M
2
(x), ïîëó÷èì óðàâíåíèå
,0
)(
)(
)(
)(
1
2
2
1
=+ dy
yN
yN
dx
xM
xM

184
â êîòîðîì ïåðåìåííûå ðàçäåëåíû. Îáùèé èíòåãðàë óðàâíåíèÿ
íàõîäèòñÿ ïî÷ëåííûì èíòåãðèðîâàíèåì:
.
)(
)(
)(
)(
1
2
2
1
Cdy
yN
yN
dx
xM
xM
=+
∫∫
Ïðèìåð 4.3. Íàéòè îáùèé èíòåãðàë óðàâíåíèÿ
cos
2
y ctg x dx + sin
2
x tg y dy = 0.
Ðåøåíèå. Ðàçäåëèì ïåðåìåííûå â äàííîì óðàâíåíèè, ïîäåëèâ
îáå åãî ÷àñòè íà âûðàæåíèå cos
2
y · sin
2
x:
.0
cos
tg
sin
ctg
22
=+ dy
y
y
dx
x
x
Èíòåãðèðóÿ îáå ÷àñòè äàííîãî óðàâíåíèÿ, ïîëó÷èì
∫∫
=+
,
cos
tg
sin
ctg
22
Cdy
y
y
dx
x
x
îòêóäà
.
2
tg
2
ctg
22
C
yx
=+
Âîñïîëüçóåìñÿ òåì, ÷òî Ñ ïðîèçâîëüíàÿ ïîñòîÿííàÿ è çàìå-
íèì Ñ íà
.
2
C
Òîãäà
tg
2
y ctg
2
x = C.
Ýòî è åñòü îáùèé èíòåãðàë äàííîãî óðàâíåíèÿ.
Ïðèìåð 4.4. Íàéòè îáùåå ðåøåíèå äèôôåðåíöèàëüíîãî óðàâ-
íåíèÿ ïåðâîãî ïîðÿäêà
.0
ln
=−
′
x
y
y
x
Ðåøåíèå. Âûðàçèì ïðîèçâîäíóþ ó′ èç óðàâíåíèÿ
.
ln xx
y
y
=
′
Ïðàâàÿ ÷àñòü ðàçëàãàåòñÿ íà ìíîæèòåëè f (x,y) =
ϕ
(x) ·
ψ
(y),
ñëåäîâàòåëüíî, ýòî óðàâíåíèå ñ ðàçäåëÿþùèìèñÿ ïåðåìåííûìè.
Ðàçäåëèì èõ
xx
y
dx
dy
ln
=
èëè
.
ln xx
dx
y
dy
=
Òåïåðü ïðîèíòåãðèðóåì
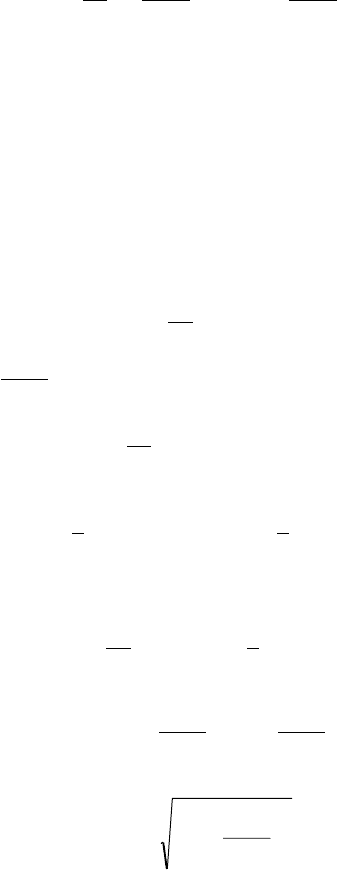
185
îáå ÷àñòè è äëÿ óäîáñòâà äîïèøåì ïîñòîÿííóþ èíòåãðèðîâà-
íèÿ â âèäå ln c.
,
ln
ln
||ln,
ln
∫∫ ∫
==
x
xd
y
xx
dx
y
dy
ln| y | = ln | ln x | + ln c (c > 0)
èëè
ln| y | = ln ñ | ln x |,
òîãäà
| y | = c | ln x |.
Îêîí÷àòåëüíî ó = ñ · ln x, ãäå ñ ëþáîå ÷èñëî. Èòàê, èñêîìîå
îáùåå ðåøåíèå ó = ñ ln x.
Ïðèìåð 4.5. Íàéòè ÷àñòíîå ðåøåíèå óðàâíåíèÿ (1 + e
x
)yy′ = e
x
,
óäîâëåòâîðÿþùåå íà÷àëüíîìó óñëîâèþ ó |
x = 0
= 1.
Ðåøåíèå. Èìååì
.
)1(
xx
eye
dx
dy
=+
Ðàçäåëÿÿ ïåðåìåííûå, ïîëó-
÷èì:
.
1
x
x
e
dxe
ydy
+
=
Èíòåãðèðóÿ, íàéäåì îáùèé èíòåãðàë:
.)1ln(
2
2
Ce
y
x
++=
Òåïåðü íàéäåì Ñ. Ïîëîæèì õ = 0, ó = 1, òîãäà
.2ln
2
1
)1ln(
2
1
0
−=⇒++= ÑCe
Ïîäñòàâëÿÿ çíà÷åíèå Ñ â âûðàæåíèå îáùåãî èíòåãðàëà, íàé-
äåì ÷àñòíûé èíòåãðàë:
2ln
2
1
)1ln(
2
2
−++=
x
e
y
èëè
,
2
1
ln1
2
1
ln21
2
2
+
+=
+
+=
xx
ee
y
îòêóäà
.
2
1
ln1
2
+
+±=
x
e
y
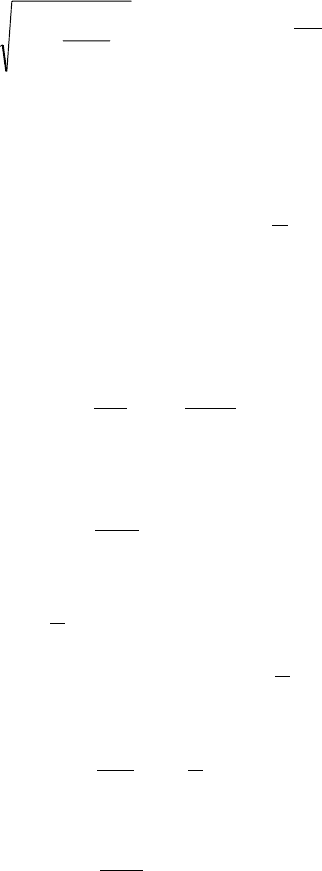
186
Èç íà÷àëüíîãî óñëîâèÿ ñëåäóåò, ÷òî y > 0 (ó |
x = 0
= 1), ïîýòîìó
ïåðåä êîðíåì áåðåì çíàê ïëþñ. Èòàê, èñêîìîå ÷àñòíîå ðåøåíèå:
.1)2(ln èëè
2
1
ln1
2
1
2
2
=
+
+=
−
y
e x
e
y
x
Ïðèìåð 4.6. Íàéòè ÷àñòíûé èíòåãðàë óðàâíåíèÿ
y′ sin
2
x ln y + y = 0,
óäîâëåòâîðÿþùèé íà÷àëüíûì óñëîâèÿì
.1
4
=
π
y
Ðåøåíèå. Íàéäåì îáùèé èíòåãðàë äàííîãî óðàâíåíèÿ. Äëÿ ýòî-
ãî ðàçäåëèì ïåðåìåííûå:
sin
2
x ln y dy + y dx = 0,
èëè
.
sin
ln
2
x
dx
dy
y
y
−=
Èíòåãðèðóÿ, ïîëó÷àåì
.ctg
2
ln
2
Cx
y
+=
Ýòî è åñòü îáùèé èíòåãðàë äàííîãî óðàâíåíèÿ. Èñïîëüçóÿ íà-
÷àëüíûå óñëîâèÿ
,1
4
=
π
y
ïîäñòàâëÿåì â âûðàæåíèå îáùåãî èí-
òåãðàëà çàäàííûå çíà÷åíèÿ ïåðåìåííûõ
,
4
π
=x
ó = 1 òåì ñàìûì
îïðåäåëÿåì çíà÷åíèå ïðîèçâîëüíîé ïîñòîÿííîé Ñ:
,
4
ctg
2
1ln
2
C+=
π
îòêóäà Ñ = 1. Èòàê, èñêîìûé ÷àñòíûé èíòåãðàë
.1ctg
2
ln
2
x
y
=
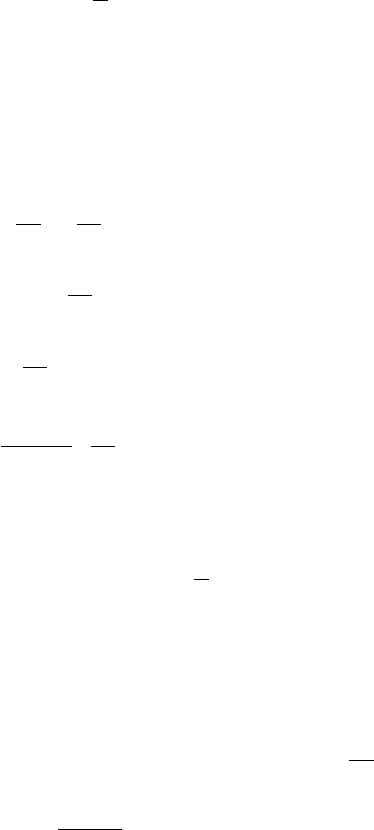
187
4.3. Îäíîðîäíûå óðàâíåíèÿ
Óðàâíåíèå âèäà
=
′
x
y
fy
(1)
íàçûâàåòñÿ îäíîðîäíûì óðàâíåíèåì.
Îäíîðîäíîå óðàâíåíèå ïðèâîäèòñÿ ê óðàâíåíèþ ñ ðàçäåëÿþ-
ùèìèñÿ ïåðåìåííûìè ïîäñòàíîâêîé y = ux, ãäå u íîâàÿ èñêî-
ìàÿ ôóíêöèÿ.
Äèôôåðåíöèðóÿ ðàâåíñòâî y = ux, ïîëó÷èì:
.u
dx
du
x
dx
dy
+=
(2)
Ïîäñòàâèâ âûðàæåíèÿ ó è
dx
dy
â óðàâíåíèå (1), èìååì:
),(ufu
dx
du
x =+
îòêóäà
.0
)(
=−
− x
dx
uuf
du
(3)
Ýòî óðàâíåíèå ñ ðàçäåëÿþùèìèñÿ ïåðåìåííûìè. Íàéäÿ îáùåå
ðåøåíèå (èíòåãðàë) óðàâíåíèÿ (3), ïîëó÷àåì îáùåå ðåøåíèå (èí-
òåãðàë) äàííîãî óðàâíåíèÿ (1), çàìåíèâ u íà
.
x
y
Ïðèìåð 4.7. Íàéòè îáùèé èíòåãðàë óðàâíåíèÿ
(x
2
+ y
2
)dx xy dy = 0.
Ðåøåíèå. Ðàçðåøèì óðàâíåíèå îòíîñèòåëüíî ïðîèçâîäíîé
:
dx
dy
.
22
xy
yx
y
+
=
′
188
Ïîäåëèâ ÷èñëèòåëü è çíàìåíàòåëü ïðàâîé ÷àñòè óðàâíåíèÿ íà
õ
2
, ïîëó÷èì:
x
y
x
y
y
2
1
+
=
′
(*)
ò.å. y′ åñòü ôóíêöèÿ îòíîøåíèÿ
.
x
y
Ýòî îçíà÷àåò, ÷òî äàííîå óðàâ-
íåíèå îäíîðîäíîå.
Äëÿ ðåøåíèÿ ýòîãî óðàâíåíèÿ ââåäåì íîâóþ ôóíêöèþ
.
x
y
u
=
Òîãäà y = ux è
.uxy
dx
du
+=
′
Óðàâíåíèå (*) ïðåîáðàçóåòñÿ â óðàâ-
íåíèå ñ ðàçäåëÿþùèìèñÿ ïåðåìåííûìè:
,
1
2
u
u
u
dx
du
x
+
=+
èëè
udx
du
x
1
=
îòêóäà
.udu
x
dx
=
Èíòåãðèðóÿ ýòî óðàâíåíèå, ïîëó÷èì
,ln
2
||ln
2
C
u
x
+=
îòêóäà
2
ln
2
u
C
x
=
ò.å.
.
2
2
u
Cex
=
Çàìåíÿÿ â ïîñëåäíåì ðàâåíñòâå u îòíîøåíèåì
,
x
y
îêîí÷àòåëü-
íî ïîëó÷èì:
.
2
2
2
x
y
Cex
=
189
Ïðèìåð 4.8. Ðàññìîòðèì ñëåäóþùèé ïðèìåð:
.
2
22
xy
yx
dx
dy +
=
Ðåøåíèå. Äåëàÿ ïîäñòàíîâêó ó = õu, ïðèâîäèì óðàâíåíèå ê âèäó:
.
2
1
2
u
u
u
dx
du
x
+
=+
Îòñþäà
u
u
u
u
u
dx
du
x
2
1
2
1
22
−
=−
+
=
è ïîòîìó
.;
;;1;
1
|;|ln|1|ln||ln;
1
2
222
22
222
2
2
CxxyCxxy
Cxyx
yx
Cx
u
C
x
Cux
u
udu
x
dx
−±=−=
=−
−
=
−
=
+−−=
−
=
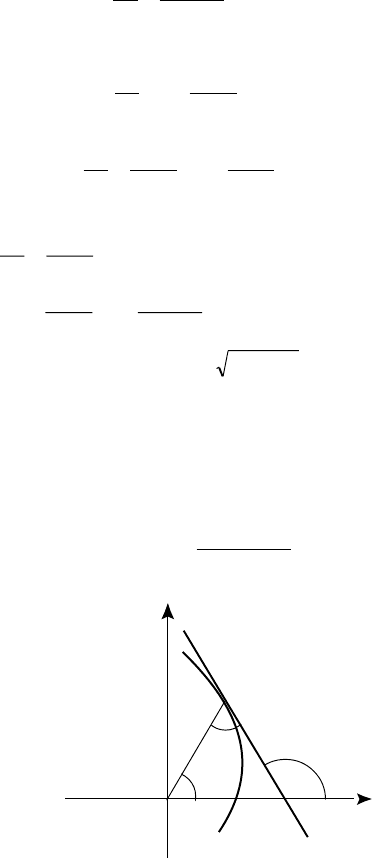
Çàäà÷à.
 òåîðèè ðåçàíèÿ âîçíèêàåò ñëåäóþùàÿ çàäà÷à: íàéòè êðèâóþ,
êàñàòåëüíàÿ ê êîòîðîé â êàæäîé òî÷êå îáðàçóåò ïîñòîÿííûé óãîë
α ñ ðàäèóñîì-âåêòîðîì ýòîé òî÷êè (ðèñ. 52). Ïî óñëîâèþ çàäà÷è
èìååì
ϕ
=
α
+
ψ
è ïîòîìó
.
tgtg1
tgtg
)(tgtg
ψα
ψα
ψαϕ
+
=+=
(1)
Ðèñ. 52
0
x
y
α
ψ
ϕ

190
Íî èç ðèñ. 52 âèäíî, ÷òî
,tg
x
y
=
ψ
à, êàê èçâåñòíî, tg
ϕ
= y′.
Ïîýòîìó ðàâåíñòâî (1) ìîæíî çàïèñàòü òàê:
,
1
x
y
k
x
y
k
y
−
+
=
′
ãäå äëÿ êðàòêîñòè ïîëîæåíî k = tg
α
. Ýòî îäíîðîäíîå óðàâíå-
íèå. Ñäåëàåì ïîäñòàíîâêó ó = õu. Ïîñëå ïðîñòûõ ïðåîáðàçîâà-
íèé ïîëó÷àåì, ÷òî
,
1
)1(
2
ku
uk
dx
du
x
−
+
=
îòêóäà íàõîäèì
.lnln)1ln(
2
1
tgarc
1
2
xCuu
k
=++−
Ïîäñòàâëÿÿ âìåñòî u çíà÷åíèå
x
y
ïîëó÷àåì ðàâåíñòâî:
.lntgarc
1
22
C
yx
x
y
k
+
=
Ýòî ðàâåíñòâî ïðîùå çàïèñàòü â ïîëÿðíûõ êîîðäèíàòàõ, ïî-
ëîæèâ x
2
+ y
2
= r
2
,
.
tg
ϕ
=
x
y
Ìû ïîëó÷èì, ÷òî
.
k
Cer
ϕ
=
Ýòà êðèâàÿ íàçûâàåòñÿ ëîãàðèôìè÷åñêîé ñïèðàëüþ.
4.4. Ëèíåéíûå óðàâíåíèÿ
Óðàâíåíèå âèäà
)()( xQyxP
dx
dy
=⋅+
(1)
íàçûâàåòñÿ ëèíåéíûì óðàâíåíèåì.
Ëèíåéíîå óðàâíåíèå ñâîäèòñÿ ê äâóì óðàâíåíèÿì ñ ðàçäåëÿþ-
ùèìèñÿ ïåðåìåííûìè çàìåíîé èñêîìîé ôóíêöèè ó ïðîèçâåäåíè-
åì äâóõ âñïîìîãàòåëüíûõ ôóíêöèé u è
υ
, ò.å. y = u
υ
.
