Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
Подождите немного. Документ загружается.

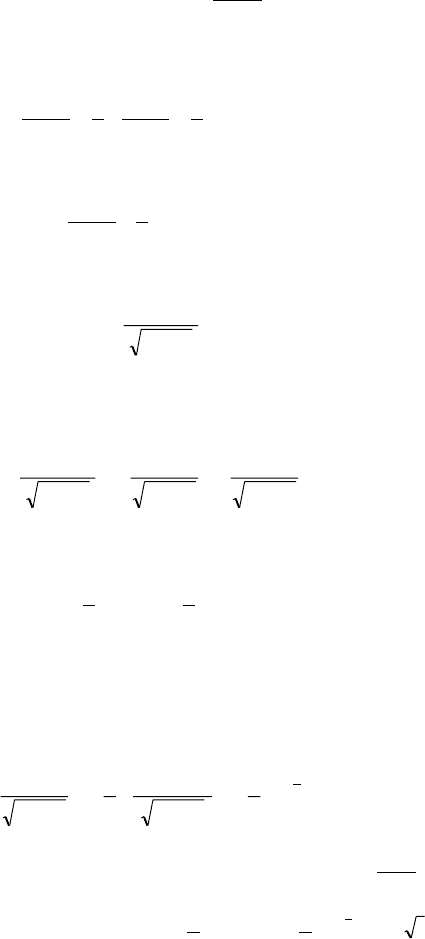
151
Ïðèìåð 3.3. Âû÷èñëèòü èíòåãðàë
∫
+
.
1
4
x
xdx
Ââåäåì íîâóþ ïåðå-
ìåííóþ èíòåãðèðîâàíèÿ u = x
2
. Òîãäà du = 2xdx, è äàííûé èíòåã-
ðàë áóäåò èìåòü âèä òàáëè÷íîãî:
.tgarc
2
1
1
2
1
1
24
Cu
u
du
x
xdx
+=
+
=
+
∫∫
Âîçâðàùàÿñü ê ñòàðîé ïåðåìåííîé èíòåãðèðîâàíèÿ, èìååì:
.arctg
2
1
1
2
4
Cx
x
xdx
+=
+
∫
Ïðèìåð 3.4. Íàéòè íåîïðåäåëåííûé èíòåãðàë
∫
−
+
2
3
)1(
x
dxx
è ïðîâåðèòü ðåçóëüòàò äèôôåðåíöèðîâàíèåì.
Ðåøåíèå. Äàííûé èíòåãðàë ðàçëîæèì íà ñóììó äâóõ èíòåã-
ðàëîâ:
.
333
)1(
222
∫∫∫
−
+
−
=
−
+
x
dx
x
xdx
x
dxx
Äëÿ âû÷èñëåíèÿ ïåðâîãî èç ýòèõ èíòåãðàëîâ âîñïîëüçóåìñÿ
òåì, ÷òî
),3(
2
1
)(
2
1
22
xdxdxdx −−==
(è òåì ñàìûì, ìíîæèòåëü õ «ïîäâåäåì ïîä çíàê äèôôåðåíöèàëà»),
è ñäåëàåì çàìåíó ïåðåìåííîé:
t = 3 x
2
.
Ïîëó÷àåì:
.
2
1
3
)3(
2
1
3
2
1
2
2
2
dtt
x
xd
x
xdx
∫∫∫
−
−=
−
−
−=
−
Ïîëó÷åííûé èíòåãðàë ÿâëÿåòñÿ òàáëè÷íûì:
∫
+
+
+
=
.
1
1
C
t
dtt
α
α
α
Ïðèìåíÿÿ ýòó ôîðìóëó ïðè
,
2
1
−=
α
èìååì:
.
2
1
2
1
Ctdtt +−=−
∫
−
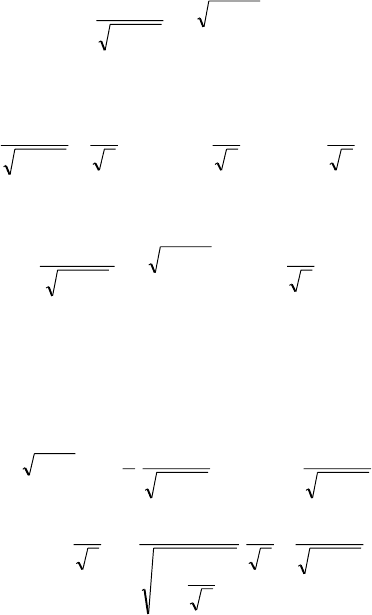
152
Âîçâðàùàÿñü ê ïåðåìåííîé õ, ïîëó÷àåì:
.3
3
2
2
Cx
x
xdx
+−−=
−
∫
Àíàëîãè÷íî âû÷èñëÿåì èíòåãðàë
.
3
sin
3
sin
3
1
3
2
C
x
arc
x
arcd
x
dx
+=
=
−
∫∫
Îêîí÷àòåëüíî èìååì:
.
3
sin3
3
)1(
2
2
C
x
arcx
x
dxx
++−−=
−
+
∫
Ïðîâåðêà. Óáåäèìñÿ, ÷òî ïðîèçâîäíàÿ îò ïîëó÷åííîãî âûðà-
æåíèÿ ñîâïàäàåò ñ ïîäèíòåãðàëüíîé ôóíêöèåé. Ïðèìåíÿÿ òàáëè-
öó ïðîèçâîäíûõ è ïðàâèëî äèôôåðåíöèðîâàíèÿ ñëîæíûõ ôóíê-
öèé, íàõîäèì:
()
.
3
1
3
1
3
1
1
3
arcsin
;
3
)3(
3
1
2
1
3
22
2
2
2
x
x
x
x
x
x
x
x
−
=
−
=
′
−
=
′
−
−
−=
′
−−
Ñêëàäûâàÿ ýòè äâà âûðàæåíèÿ, ïîëó÷àåì ïîäèíòåãðàëüíóþ
ôóíêöèþ. Ñëåäîâàòåëüíî, èíòåãðèðîâàíèå âûïîëíåíî ïðàâèëüíî.
3.1.4. Ìåòîä èíòåãðèðîâàíèÿ ïî ÷àñòÿì
Ïðèìåíåíèå ýòîãî ìåòîäà îñíîâûâàåòñÿ íà ôîðìóëå:
∫∫
−= )()()()()()( xduxvxvxuxdvxu
èëè
.duvuvdvu
∫∫
−=
(3.3)
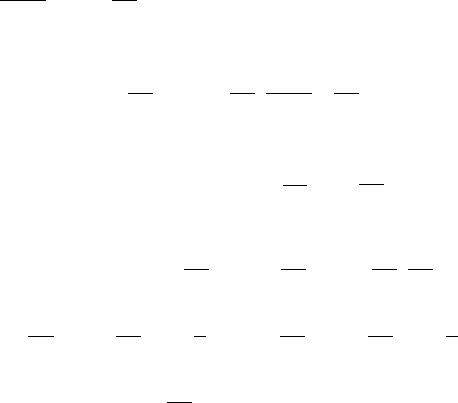
153
ßñíî, ÷òî ýòó ôîðìóëó èìååò ñìûñë ïðèìåíÿòü ëèøü òîãäà,
êîãäà èíòåãðàë
∫
vdu
îêàçûâàåòñÿ áîëåå óäîáíûì äëÿ èíòåãðèðî-
âàíèÿ (âîçìîæíî äàæå, òàáëè÷íûì), ÷åì èñõîäíûé èíòåãðàë
∫
.udv
Âîçíèêàåò âîïðîñ: êàê ïðåäñòàâèòü ïîäõîäÿùèì îáðàçîì ïîäèí-
òåãðàëüíîå âûðàæåíèå f (x)dx â âèäå u(x)dv(x). Îáùåãî ïðàâèëà
äëÿ ýòîãî íåò. Îäíàêî ìîæíî ïîëüçîâàòüñÿ ñëåäóþùèìè ÷àñòíû-
ìè óêàçàíèÿìè:
1. Åñëè ïîäèíòåãðàëüíîå âûðàæåíèå ñîäåðæèò ïðîèçâåäåíèå
ïîêàçàòåëüíîé (å
àõ
) èëè òðèãîíîìåòðè÷åñêîé ôóíêöèè (sin ax,
cos ax) íà ìíîãî÷ëåí, òî çà ìíîæèòåëü u(x) ñëåäóåò ïðèíÿòü ìíî-
ãî÷ëåí.
2. Åñëè ïîäèíòåãðàëüíîå âûðàæåíèå ñîäåðæèò ïðîèçâåäåíèå
ëîãàðèôìè÷åñêîé (ln ax) èëè îáðàòíîé òðèãîíîìåòðè÷åñêîé ôóí-
êöèè (arcsin ax, arccos ax è ò.ä.) íà ìíîãî÷ëåí, òî çà ìíîæèòåëü
u(x) ñëåäóåò ïðèíÿòü ëîãàðèôìè÷åñêóþ èëè îáðàòíóþ òðèãîíî-
ìåòðè÷åñêóþ ôóíêöèþ.
Ïðèìåð 3.5.
.
2
ln
dxxx ⋅⋅
∫
Ïðèìåíèì ôîðìóëó èíòåãðèðîâàíèÿ
ïî ÷àñòÿì
.duuuvdvu
∫∫
⋅−=⋅
Ïîëîæèì u = ln
2
x, dv = xdx, òîãäà
.
2
ln2
2
,
x
x
x
vdxdu
==
Ïî ôîðìóëå ïîëó÷èì:
.lnln
2
ln2
2
ln
2
ln
2
22
2
2
2
dxxxx
x
x
xx
x
x
dxxx
∫∫∫
⋅−=⋅−=
Ñíîâà ïðèìåíèì ôîðìóëó èíòåãðèðîâàíèÿ ïî ÷àñòÿì, ïîëî-
æèâ u = ln x, dv = xdx. Òîãäà
,
x
dx
du
=
.
2
2
x
v
=
Òîãäà
.
4
1
ln
2
ln
22
1
ln
2
ln
2
2
ln
2
ln
2
ln
2
2
2
22
2
2
22
2
2
2
Cxx
x
x
x
dxxx
x
x
x
x
dxx
x
x
x
x
dxxx
++−=+−=
=
⋅−−=
∫
∫∫
Èòàê,
.)1ln2ln2(ln
2
2
2
4
Cxxdxxx
x
++−=
∫

154
Ïðèìåð 3.6. Íàéòè èíòåãðàë
∫
.
22
dxex
x
Ïîëàãàåì u = x
2
. Îñòàâøååñÿ ïîä èíòåãðàëîì âûðàæåíèå
îáîçíà÷àåì ÷åðåç dv è ïðåîáðàçóåì åãî ñ ïîìîùüþ ïðèåìà «ïîä-
âåäåíèÿ ôóíêöèè ïîä çíàê äèôôåðåíöèàëà»:
.
2
2
2
==
x
x
e
ddxedv
Äëÿ ïðèìåíåíèÿ ôîðìóëû èíòåãðèðîâàíèÿ âî ÷àñòÿì âû÷èñ-
ëèì du è v:
∫
==== .
2
,2)(
2
2
x
e
dvvxdxxddu
Ñîãëàñíî ôîðìóëå èíòåãðèðîâàíèÿ ïî ÷àñòÿì, èìååì:
.2
22
22
222
∫∫
⋅−= xdx
ee
xdxex
xx
x
Èòàê, èñõîäíûé èíòåãðàë ñâåëñÿ ê âû÷èñëåíèþ èíòåãðàëà
.
2
∫
xdxe
x
Ê íåìó âíîâü ïðèìåíÿåì ôîðìóëó èíòåãðèðîâàíèÿ ïî ÷àñòÿì:
.
22
22
2
∫∫
−= dx
ee
xdxex
xx
x
Èòàê, ïîëó÷èëè èíòåãðàë òàáëè÷íîãî âèäà:
.
4
1
)2(
4
1
2
1
2
222
2
Cexdedxedx
e
xxx
x
+===
∫∫∫
Ñóììèðóÿ ïðîâåäåííûå âû÷èñëåíèÿ, èìååì îêîí÷àòåëüíî:
.
4
1
2
1
2
1
222222
Cexeexdxex
xxxx
++−=
∫
Ïðèìåð 3.7. Íàéòè èíòåãðàë
∫
.ln
2
dxx
Ïðèíèìàåì u = ln
2
x è dv = dõ, òîãäà
,
1
ln2 dx
x
xdu =
à
∫
== xdxv
è, ïðèìåíÿÿ ôîðìóëó (3.3), èìååì:
.ln2lnln
2
lnln
222
∫∫∫
−=⋅−=
dxxxxdxx
x
xxxdxx

155
Èíòåãðàë
∫
dxxln
íàõîäèì ïî ÷àñòÿì, ïðèíèìàÿ u = ln x è
dv = dõ. Èìåÿ â âèäó, ÷òî
x
dx
du =
è v = x, èñïîëüçóÿ âòîðîé ðàç
ôîðìóëó (3.3.), ïîëó÷èì:
,)1(lnlnlnln
11
CxxCxxx
x
dx
xxxdxx +−=+−=−=
∫∫
à èñêîìûé èíòåãðàë áóäåò èìåòü ñëåäóþùèé âèä:
.)1(ln2lnln
22
Cxxxxdxx +−−=
∫
3.1.5. Èíòåãðèðîâàíèå äðîáíî-ðàöèîíàëüíûõ ôóíêöèé
Äðîáíî-ðàöèîíàëüíîé ôóíêöèåé (ðàöèîíàëüíîé äðîáüþ) íà-
çûâàåòñÿ îòíîøåíèå äâóõ ìíîãî÷ëåíîâ. Åñëè ñòåïåíü ìíîãî÷ëå-
íà, ñòîÿùåãî â ÷èñëèòåëå äðîáè, íå ìåíüøå, ÷åì ñòåïåíü ìíîãî-
÷ëåíà â çíàìåíàòåëå, òî â ýòîé äðîáè ñëåäóåò âûäåëèòü öåëóþ ÷àñòü,
ò.å. ïðåäñòàâèòü åå â âèäå:
,
)(
)(
)(
xQ
xP
xR +
ãäå R(x), P(x), Q(x) ìíîãî÷ëåíû, ïðè÷åì ñòåïåíü P(x) ìåíüøå
ñòåïåíè Q(x). Ðàöèîíàëüíàÿ äðîáü
,
)(
)(
xQ
xP
îáëàäàþùàÿ ýòèì ñâîé-
ñòâîì, íàçûâàåòñÿ ïðàâèëüíîé. Äëÿ èíòåãðèðîâàíèÿ òàêîé äðîáè
åå íåîáõîäèìî ðàçëîæèòü â ñóììó ïðîñòåéøèõ äðîáåé, êîòîðûå
ëåãêî èíòåãðèðóþòñÿ:
,04,
)(
,
)(
1
1
)()(
,||ln
2
2
1
<−
++
+
+
−
⋅
−
−=
−−
+−=
−−
∫
∫
−
qp
qpxx
DCx
C
bx
k
B
dx
bx
B
bx
B
CaxAdx
ax
A
ax
A
k
kkk
ò.å. ýòîò êâàäðàòíûé òðåõ÷ëåí íå èìååò äåéñòâèòåëüíûõ êîðíåé
(èíòåãðèðîâàíèå ïðîñòåéøèõ äðîáåé ïîñëåäíåãî òèïà áóäåò ïî-

156
êàçàíî íèæå íà ïðèìåðå). Îñòàíîâèìñÿ ïîäðîáíåå íà ìåòîäèêå
ðàçëîæåíèÿ ïðàâèëüíîé ðàöèîíàëüíîé äðîáè
)(
)(
xQ
xP
â ñóììó ïðî-
ñòåéøèõ äðîáåé. Ýòî âûïîëíÿåòñÿ ïî ñëåäóþùåé ñõåìå:
1. Ñíà÷àëà çíàìåíàòåëü äðîáè Q(x) íåîáõîäèìî ðàçëîæèòü íà
ìíîæèòåëè âèäà: x a, (x b)
k
, (x
2
+ px + q)
k
.
Ïðè ýòîì ÷àñòî èñïîëüçóåòñÿ òåîðåìà Âèåòà: åñëè êâàäðàòíûé
òðåõ÷ëåí ax
2
+ bx + c èìååò êîðíè õ
1
, õ
2
, òî
ax
2
+ bx + c = à(õ õ
1
)(õ õ
2
).
2. Äàëåå ñëåäóåò çàïèñàòü ðàçëîæåíèå äðîáè
)(
)(
xQ
xP
â ñóììó ïðî-
ñòåéøèõ äðîáåé, îñòàâëÿÿ íåîïðåäåëåííûìè êîýôôèöèåíòàìè À,
B, C, D è ò.ä. Ïðè ýòîì êàæäîìó ìíîæèòåëþ âèäà (x à) ñîîòâåò-
ñòâóåò äðîáü
ax
A
−
, ìíîæèòåëþ âèäà (x b)
k
ñîîòâåòñòâóåò ñóììà
äðîáåé:
,
)(
...
k
bx
C
bx
B
−
++
−
à ìíîæèòåëþ âèäà x
2
+ px + q, åñëè îí íå èìååò äåéñòâèòåëüíûõ
êîðíåé (p
2
4q < 0), ñîîòâåòñòâóåò äðîáü âèäà:
.
2
qpxx
EDx
++
+
3. Äëÿ îïðåäåëåíèÿ êîýôôèöèåíòîâ À, B, C, D, Å â ýòîì ðàçëî-
æåíèè ñëåäóåò ïðèðàâíÿòü êîýôôèöèåíòû ïðè îäèíàêîâûõ ñòåïå-
íÿõ õ ó ìíîãî÷ëåíà P(x) è ìíîãî÷ëåíà, êîòîðûé ïîëó÷àåòñÿ â ÷èñ-
ëèòåëå ïîñëå ïðèâåäåíèÿ çàïèñàííîé ñóììû ïðîñòåéøèõ äðîáåé ê
îáùåìó çíàìåíàòåëþ (ìåòîä íåîïðåäåëåííûõ êîýôôèöèåíòîâ).
Ìîæíî òàêæå íàõîäèòü ýòè êîýôôèöèåíòû ïóòåì ñðàâíåíèÿ çíà-
÷åíèé óêàçàííûõ ìíîãî÷ëåíîâ ïðè êîíêðåòíûõ çíà÷åíèÿõ õ (â ïåð-
âóþ î÷åðåäü, ïðè õ, ñîâïàäàþùèõ ñ êîðíÿìè çíàìåíàòåëÿ Q(x)).
Ïðèìåð 3.8. Âû÷èñëèòü èíòåãðàë
∫
++
.
84
2
3
xx
dxx
Ïîäèíòåãðàëü-
íàÿ ôóíêöèÿ ïðåäñòàâëÿåò ñîáîé íåïðàâèëüíóþ ðàöèîíàëüíóþ

157
äðîáü, ïîýòîìó âûäåëèì ñíà÷àëà öåëóþ ÷àñòü äðîáè, ïîäåëèâ ñ
îñòàòêîì ÷èñëèòåëü íà çíàìåíàòåëü
84
84
84
2
2
23
3
++
−−
++
−
xx
xx
xxx
x
Òàêèì îáðàçîì
84
328
4
84
22
3
++
+
+−=
++ xx
x
x
xx
x
è
.
84
4
84
2
84
)4(
84
84
2
2
22
3
dx
xx
x
x
x
xx
dxx
dxxxd
xx
dxx
∫
∫∫∫∫
++
+
+−=
=
++
+
+−=
++
Äëÿ íàõîæäåíèÿ îñòàâøåãîñÿ èíòåãðàëà âûäåëèì â ÷èñëèòåëå
äèôôåðåíöèàë çíàìåíàòåëÿ d(x
2
+ 4x + 8) = (2x + 4)dx.
Çàòåì ðàçîáüåì èíòåãðàë íà äâà ñëàãàåìûõ è â ïîñëåäíåì âû-
äåëèì ïîëíûé êâàäðàò êâàäðàòíîãî òðåõ÷ëåíà, ñòîÿùåãî â çíàìå-
íàòåëå. Òåì ñàìûì ïîëó÷èì:
.
2
2
tgarc8)84ln(44
2
4)2(
)2(
16
84
)84(
44
2
4)44(
4
4
84
)42(
44
2
84
4)42(
44
2
84
2
2
22
22
22
2
2
2
2
3
C
x
xxx
x
x
xd
xx
xxd
x
x
xx
dx
xx
dxx
x
x
dx
xx
x
x
x
xx
dxx
+
+
++++−=
=
++
+
+
++
++
+−=
=
+++
+
++
+
+−=
=
++
++
+−=
++
∫∫
∫∫
∫∫
x 4 (öåëàÿ ÷àñòü )
(îñòàòîê).
328
32164
2
+
−−−
x
xx

158
Ïðèìåð 3.9. Âû÷èñëèòü èíòåãðàë
.
485
23
2
∫
+++
xxx
dxx
1. Ïîäèíòåãðàëüíàÿ ôóíêöèÿ ïðàâèëüíàÿ ðàöèîíàëüíàÿ
äðîáü.
2. Ðàçëîæèì çíàìåíàòåëü ïðàâèëüíîé ðàöèîíàëüíîé äðîáè íà
ïðîñòåéøèå äåéñòâèòåëüíûå ìíîæèòåëè:
x
3
+ 5x
2
+ 8x + 4 = x
3
+ 4x
2
+ x
2
+ 4x + 4x + 4 =
=x(x
2
+ 4x + 4) + (x
2
+ 4x + 4) = (x + 2)
2
(x + 1).
3. Ðàçëîæèì ïðàâèëüíóþ ðàöèîíàëüíóþ äðîáü íà ïðîñòåéøèå:
.
12
)2()1()2(
1
2
0
2
2
+
+
+
+
+
=
++
x
B
x
A
x
A
xx
x
Òàê êàê â çíàìåíàòåëå ïðàâèëüíîé äðîáè åñòü êðàòíûé ëè-
íåéíûé ìíîæèòåëü, òî â ðàçëîæåíèè ïîÿâèëàñü ïðîñòåéøàÿ äðîáü
II òèïà.
4. Ïðèâåäåì ê îáùåìó çíàìåíàòåëþ âñå äðîáè è çàòåì îòáðî-
ñèì åãî:
x
2
= À
0
(x + 1) + À
1
(x + 1)(x + 2) + Â(x + 2)
2
=
= À
0
x + À
0
+ À
1
x
2
+ 3À
1
x
+ 2À
1
+ Âõ
2
+ 4Âx
+ 4Â.
Òàêèì îáðàçîì, èìååì
x
2
= (À
1
+ Â)x
2
+ (À
0
+ 3À
1
+ 4Â)x + (À
0
+ 2À
1
+ 4Â).
5. Ñîñòàâëÿåì ñèñòåìó óðàâíåíèé:
BAA
BAA
BA
x
x
420
430
1
÷ë. câ.
10
10
1
1
2
++=
++=
+=
6. Ðåøàÿ ñèñòåìó óðàâíåíèé, ïîëó÷èì À
0
= 4, À
1
= 0 è Â = 1,
à èñõîäíàÿ ïîäèíòåãðàëüíàÿ ôóíêöèÿ ðàçëîæèòñÿ íà ïðîñòåéøèå
äðîáè ñëåäóþùèì îáðàçîì:
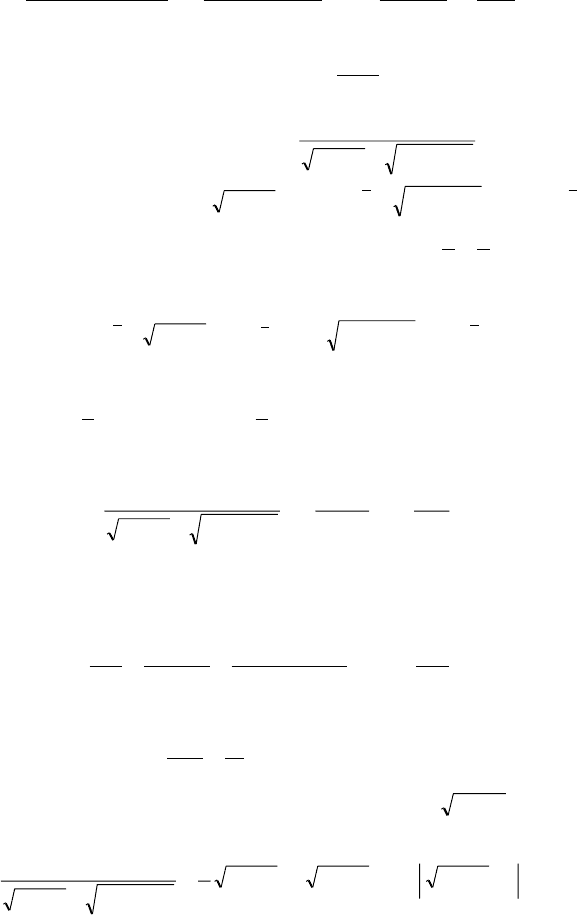
.
1
1
2
0
)2(
4
)2)(1(
22
2
+
+
+
+
+
−
=
++
xx
xxx
x
159
7. Âû÷èñëÿåì çàäàííûé èíòåãðàë:
.|1|ln
2
4
|1|ln)2()2(4
1
)2(
4
)2)(1(485
2
22
2
23
2
Cx
x
xxdx
x
dx
x
dx
xx
dxx
xxx
dxx
+++
+
=++++−=
=
+
+
+
−=
++
=
+++
∫
∫∫∫∫
−
Ïðèìåð 3.10. Íàéòè èíòåãðàë
.
)32(32
3
2
∫
+++
xx
dx
Ðåøåíèå. Çàìåòèì, ÷òî
,)32(32
2
1
+=+ xx
.)32()32(
3
2
3
2
+=+ xx
Íàèìåíüøèì îáùèì êðàòíûì çíàìåíàòåëåì äðîáåé
,
2
1
3
2
ÿâëÿåòñÿ
6. Ïîýòîìó, åñëè ïðèìåíèòü ïîäñòàíîâêó 2õ + 3 = t
6
, òî áóäåò èìåòü:
,)32(
6
1
+= xt
,)(32
36
2
1
ttx ==+
,)()32(
4
3
2
6
3
2
ttx ==+
ò.å. èððàöèîíàëüíîñòè â ïîäèíòåãðàëüíîì âûðàæåíèè èñ÷åçàþò.
Òàê êàê:
),3(
2
1
6
−= tx òî
.36
2
1
55
dttdttdx ==
Ïîäñòàâëÿÿ íàéäåííûå âûðàæåíèÿ â èñêîìûé èíòåãðàë,
ïîëó÷àåì:
.
1
3
3
)32(32
2
43
5
3
2
∫∫∫
+
=
+
=
+++
t
dtt
tt
dtt
xx
dx
Òàêèì îáðàçîì, äàííûé èíòåãðàë ñâåäåí ê èíòåãðàëó îò ðàöè-
îíàëüíîé ôóíêöèè. Äëÿ åãî íàõîæäåíèÿ âûäåëèì öåëóþ ÷àñòü
ïîäèíòåãðàëüíîé ôóíêöèè:
.
1
1
1
1
1)1)(1(
1
11
1
22
+
+−=
+
++−
=
+
+−
=
+ t
t
t
tt
t
t
t
t
Èíòåãðèðóÿ êàæäîå èç ñëàãàåìûõ, íàõîäèì:
.|1|ln
21
22
Ctt
t
t
dtt
+++−=
+
∫
Âîçâðàòèìñÿ ê ñòàðîé ïåðåìåííîé. Òàê êàê
,32
6
+= xt
òî ïî-
ëó÷àåì ñëåäóþùèé îêîí÷àòåëüíûé ðåçóëüòàò:
.132ln332332
2
3
)32(32
663
3
2
Cxxx
xx
dx
+++++−+=
+++
∫
160
Ïðèìåð 3.11. Íàéòè èíòåãðàë
.
12cos
sinsin
3
dx
x
xx
∫
−
−
Òàê êàê cos 2x = 2cos
2
x 1, òî ïîäèíòåãðàëüíàÿ ôóíêöèÿ èìå-
åò âèä R(sin x, cos x). Çàìåòèì, ÷òî ïðè çàìåíå sin x íà sin x îíà
ìåíÿåò çíàê, ò.å. ÿâëÿåòñÿ íå÷åòíîé îòíîñèòåëüíî sin x. Ïðèìåíÿ-
åì ïîäñòàíîâêó cos x = t. Òîãäà
.
22
sin
2cos2
)1(sinsin
12cos
sinsin
,1sin,
sin
2
2
2
2
3
22
dt
t
t
x
dt
x
xx
dx
x
xx
tx
x
dt
dx
−
=
−
−
−
=
=
−
−
−=−=
Èòàê, ïîäèíòåãðàëüíîå âûðàæåíèå ïðåîáðàçîâàíî ê äðîáíî-
ðàöèîíàëüíîìó âèäó. Âûäåëÿåì öåëóþ ÷àñòü è ðàçëîæèì íà ïðî-
ñòåéøèå äðîáè:
.
1
1
1
1
4
1
2
1
)1)(1(
1
2
1
2
1
)1(2
11
22
2
2
2
2
+
−
−
+=
+−
+=
−
+−
=
−
tttt
t
t
t
t
Îòñþäà
.
1
1
ln
4
1
2
22
2
2
C
t
tt
t
dtt
+
+
−
+=
−
∫
Âîçâðàùàÿñü ê ñòàðîé ïåðåìåííîé x cos x = t, íàõîäèì:
.
1cos
1cos
ln
4
1
2
cos
12cos
sinsin
3
C
x
xx
dx
x
xx
+
+
−
+=
−
−
∫
3.2. Îïðåäåëåííûé èíòåãðàë
3.2.1. Îñíîâíûå ïîíÿòèÿ è ñâîéñòâà
Ïóñòü y = f(x) íåïðåðûâíàÿ íà [a, b] ôóíêöèÿ. Ðàçîáüåì [a, b]
òî÷êàìè à = õ
0
< õ
1
< õ
2
< < õ
n 1
< õ
n
= b íà n ÷àñòè÷íûõ
îòðåçêîâ
[à, õ
1
], [õ
1
, õ
2
], , [õ
n 1
, b].
 êàæäîì èç íèõ âûáåðåì ïî îäíîé ïðîèçâîëüíîé òî÷êå
ξ
1
∈ [à, õ
1
],
ξ
2
∈ [õ
1
, õ
2
], ,
ξ
n
∈ [õ
n 1
, b].
