Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
Подождите немного. Документ загружается.

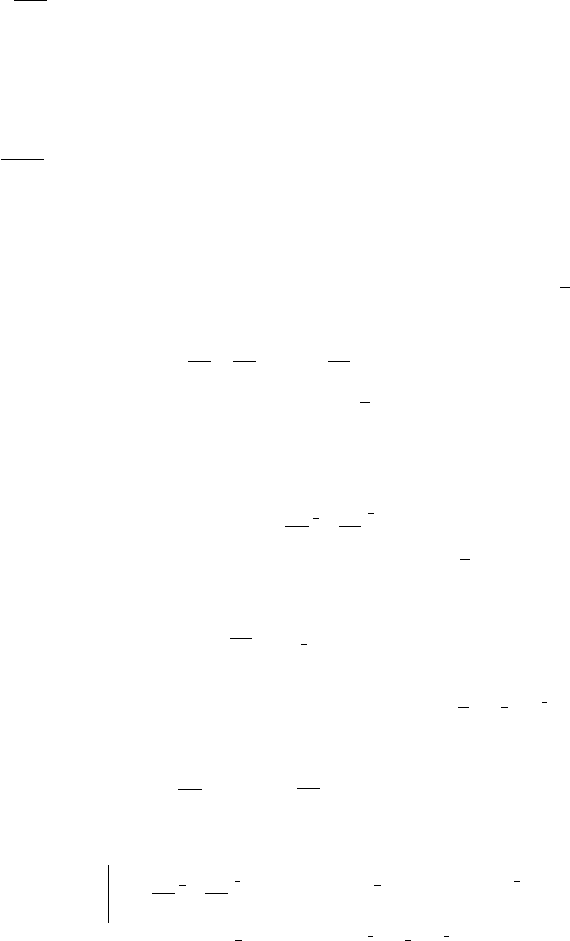
171
.cos4sin2
)(cos2sin2
)(sin2sin)2()sin2(
25210255
25255255
255255255
2
2
yxyxyxx
yxyxyxyxx
yxyxyxyxyxyx
y
z
y
yyy
=
=
′
⋅⋅=
=
′
⋅−⋅
′
=
′
=
∂
∂
.cos10sin10
)(cos5sin10
)(sin5sin)5()sin5(
2539254
252524254
252425242524
2
yxyxyxyx
yxyxyxyxyx
yxyxyxyxyxyx
yx
z
y
yyy
=
=
′
⋅=
=
′
−⋅
′
=
′
=
∂∂
∂
Ïðîèçâîäíîé ôóíêöèè z = f(x, y) â äàííîì íàïðàâëåíèè
a
íà-
çûâàåòñÿ:
,sincos
αα
⋅
∂
∂
+⋅
∂
∂
=
∂
∂
y
z
x
z
a
z
(3.11)
ãäå a óãîë, îáðàçîâàííûé âåêòîðîì
a
ñ îñüþ Îx.
Ãðàäèåíòîì ôóíêöèè z = f(x, y) íàçûâàåòñÿ âåêòîð, ïðîåêöèÿ-
ìè êîòîðîãî íà êîîðäèíàòíûå îñè ÿâëÿþòñÿ ñîîòâåòñòâóþùèå
÷àñòíûå ïðîèçâîäíûå äàííîé ôóíêöèè:
.grad j
y
z
x
z
z
∂
∂
+
∂
∂
=
ι
(3.12)
Ïðîèçâîäíàÿ äàííîé ôóíêöèè â íàïðàâëåíèè
a
ñâÿçàíà ñ ãðà-
äèåíòîì ôóíêöèè ñëåäóþùåé ôîðìóëîé:
.grad z
a
z
a
P
Π=
∂
∂
(3.13)
Ïðèìåð 3.25. Íàéòè ãðàäèåíò ôóíêöèè z = x
2
xy + y
3
â òî÷êå
À(1;1) è ïðîèçâîäíóþ ïî íàïðàâëåíèþ âåêòîðà
.43
ja
−=
ι
Ðåøåíèå. ×àñòíûå ïðîèçâîäíûå ðàâíû:
,2 yx
x
z
−=
∂
∂
.3
2
yx
y
z
+−=
∂
∂
Ïî ôîðìóëå (3.12):
()
()
.23)1(31(-1)-12
)3()2(grad
2
2
jj
jyxyxj
y
z
x
z
z
AA
A
A
+=−+−+⋅=
=⋅+−+⋅−=
∂
∂
+
∂
∂
=
ιι
ιι

172
Ïðîèçâîäíàÿ ïî íàïðàâëåíèþ ïî ôîðìóëå (3.11) ðàâíà:
()
.
5
1
)4(233
5
1
)4(3
)4(
)4(3
3
2222
=−+⋅=
−+
−
⋅
∂
∂
+
−+
⋅
∂
∂
=
∂
∂
y
z
x
z
a
z
Èñïîëüçóÿ ÷àñòíûå ïðîèçâîäíûå, ìîæíî ðåøàòü çàäà÷è íà
îòûñêàíèå ýêñòðåìóìà ôóíêöèè íåñêîëüêèõ ïåðåìåííûõ.
Òî÷êè, â êîòîðûõ äèôôåðåíöèðóåìàÿ ôóíêöèÿ f (x; y) ìîæåò
äîñòèãàòü ýêñòðåìóìà (òàê íàçûâàåìûå ñòàöèîíàðíûå òî÷êè), íà-
õîäÿòñÿ ïóòåì ðåøåíèÿ ñèñòåìû óðàâíåíèé
=
′
=
′
0);(
,0);(
yxf
yxf
y
x
(3.14)
(íåîáõîäèìûå óñëîâèÿ ýêñòðåìóìà).
Äîñòàòî÷íûå óñëîâèÿ ñóùåñòâîâàíèÿ ýêñòðåìóìà ôóíêöèè äâóõ
ïåðåìåííûõ çàêëþ÷àþòñÿ â ñëåäóþùåì: ïóñòü
0);();( =
′
=
′
bafbaf
yx
è
),;( bafA
xx
′′
=
),;( bafB
xy
′′
=
).;( bafC
yy
′′
=
Ñîñòàâèì äèñêðèìèíàíò
∆ = À · Ñ Â
2
.
Òîãäà: 1) åñëè ∆ > 0, òî ôóíêöèÿ èìååò ýêñòðåìóì â òî÷êå P(a; b),
à èìåííî, ìàêñèìóì, åñëè A < 0 (èëè Ñ < 0), è ìèíèìóì, åñëè À > 0
(èëè Ñ > 0); 2) åñëè ∆ < 0, òî ýêñòðåìóìà â òî÷êå P íåò;
3) åñëè ∆ = 0, òî âîïðîñ î íàëè÷èè ýêñòðåìóìà â òî÷êå P îñòàåòñÿ
îòêðûòûì (òðåáóåòñÿ äàëüíåéøåå èññëåäîâàíèå).
Ïðèìåð 3.26. Íàéòè ýêñòðåìóìû ôóíêöèè
z = e
x
· (4y xy y
2
).
Ðåøåíèå. Îïðåäåëèì ñòàöèîíàðíûå òî÷êè z, ðåøàÿ ñèñòåìó
=−−
=−−
=−−
=−−
=−−
=−−
=−−
=−+−−
=
∂
∂
=
∂
∂
.024
,0)3(
,024
,03
,0)24(
,0)3(
.0)24(
,0)()4(
.0
;0
2
2
2
yx
yxy
yx
yxyy
yxe
yxyye
yxe
yeyxyye
y
z
x
z
x
x
x
xx
À
ÀÀ

173
Ýòà ñèñòåìà èìååò ðåøåíèå, åñëè
=
=
=−−
=
4
,0
,024
,0
x
y
yx
y
èëè, åñëè
=
=
=−
−=
=−−−
−=
=−−
=−−
.1
,2
,01
,3
,02)3(4
,3
,024
,03
y
x
y
yx
yy
yx
yx
yx
Òàêèì îáðàçîì, z èìååò äâå ñòàöèîíàðíûå òî÷êè: À (4; 0)
è B (2; 1).
Èñïîëüçóåì äîñòàòî÷íûå óñëîâèÿ ýêñòðåìóìà. Äëÿ ýòîãî íàé-
äåì ÷àñòíûå ïðîèçâîäíûå z âòîðîãî ïîðÿäêà.
[]
[]
[]
.2)2()24(
),23()3(
),2()()3()3(
2
2
2
2
222
2
2
xxx
xx
xxxx
ee
y
xe
y
z
y
xe
y
x
y
y
e
y
x
z
y
x
y
y
e
y
e
y
x
y
y
e
y
x
y
y
e
x
z
−=−=−−=
∂
∂
−−=−−=
∂∂
∂
−−=−+−−=−−=
∂
∂
Òîãäà
[]
0)1()2(0
8
2
444
2
2
2
2
2
2
<−=−⋅−−⋅⋅=
∂∂
∂
−
∂
∂
⋅
∂
∂
=∆ eeee
yx
z
y
z
x
z
A
A
è â òî÷êå A íåò ýêñòðåìóìà.
.2)()2()(
4442222
2
2
2
2
2
2
eeeeee
yx
z
y
z
x
z
B
B
=−=−−−⋅−=
∂∂
∂
−
∂
∂
⋅
∂
∂
=∆
Òàê êàê ∆
B
> 0 è
,0
2
2
2
<−=
∂
∂
e
x
z
B
òî â òî÷êå  ôóíêöèÿ z
èìååò ìàêñèìóì.
Òàêèì îáðàçîì ôóíêöèÿ z = e
x
(4y xy y
2
) èìååò åäèíñòâåí-
íûé ýêñòðåìóì ìàêñèìóì â òî÷êå  (2; 1).
′
x
′
y
′
y
174
3.4. Äâîéíûå èíòåãðàëû
Ñâîéñòâà äâîéíîãî èíòåãðàëà è åãî âû÷èñëåíèå â äåêàðòîâûõ
ïðÿìîóãîëüíûõ êîîðäèíàòàõ. Ïóñòü ôóíêöèè f(x, y) = f(P) îïðå-
äåëåíà è íåïðåðûâíà íà çàìêíóòîé îãðàíè÷åííîé îáëàñòè G ïëîñ-
êîñòè 0xy,
σ
n
= {∆
σ
1
, ∆
σ
2
, , ∆
σ
n
} íåêîòîðîå ðàçáèåíèå îáëà-
ñòè G íà ýëåìåíòàðíûå ïîäîáëàñòè ∆
σ
k
, ïëîùàäè êîòîðûõ òàêæå
îáîçíà÷èì ÷åðåç ∆
σ
k
, à äèàìåòðû ÷åðåç d
k
. Çàôèêñèðóåì òî÷êè
P
k
∈∆
σ
k
, k = 1, , n. Âûðàæåíèå
∑
=
∆=
n
k
kkn
P
f
S
1
)(
σ
íàçûâàåòñÿ èíòåãðàëüíîé ñóììîé äëÿ ôóíêöèè f(P) ïî îáëàñòè G.
Åñëè ñóùåñòâóåò ïðåäåë ïîñëåäîâàòåëüíîñòè èíòåãðàëüíûõ ñóìì
S
n
ïðè
0max
1
→
≤≤
nk
k
d
(ïðè ýòîì n → ∞) è åñëè ýòîò ïðåäåë íå çàâèñèò
íè îò ñïîñîáà ðàçáèåíèÿ îáëàñòè G íà ýëåìåíòàðíûå ïîäîáëàñòè
∆
σ
k
, íè îò âûáîðà òî÷åê P
k
∈ ∆
σ
k
, òî îí íàçûâàåòñÿ äâîéíûì èí-
òåãðàëîì îò ôóíêöèè f(x, y) ïî îáëàñòè G è îáîçíà÷àåòñÿ ÷åðåç
∫
∫
G
dydxyxf
.),(
Òàêèì îáðàçîì,
.)(lim),(
1
max
0
∑
∫∫
=
∆=
→
n
k
kk
G
d
P
f
d
y
dx
y
x
f
k
σ
Äëÿ äâîéíîãî èíòåãðàëà ñïðàâåäëèâû ñâîéñòâà ëèíåéíîñòè è
àääèòèâíîñòè.
Âû÷èñëåíèå äâîéíîãî èíòåãðàëà ñâîäèòñÿ ê âû÷èñëåíèþ ïîâòîð-
íûõ èíòåãðàëîâ ñëåäóþùèì ñïîñîáîì. Ïóñòü îáëàñòü G (ðèñ. 45)
îãðàíè÷åíà êðèâûìè y =
ϕ
1
(x), y =
ϕ
2
(x), õ = à, x = b, ïðè÷åì âñþäó
íà [a, b] ôóíêöèè
ϕ
1
(x) è
ϕ
2
(x) íåïðåðûâíû è
ϕ
1
(x) ≤
ϕ
2
(x).
Òîãäà
,),(),(
)(
)(
2
1
∫∫∫∫
=
x
x
b
aG
d
y
y
x
f
dxd
y
dx
y
x
f
ϕ
ϕ
(3.15)
ïðè÷åì ñíà÷àëà âû÷èñëÿåòñÿ âíóòðåííèé èíòåãðàë ïî ïåðåìåííîé
y (x ïàðàìåòð), à ïîëó÷åííûé ðåçóëüòàò èíòåãðèðóåòñÿ ïî x.
Çàìåòèì ïðè ýòîì, ÷òî åñëè êðèâàÿ
ϕ
1
(x) (èëè êðèâàÿ
ϕ
2
(x)) â

175
ïðîìåæóòêå à ≤ x ≤ b çàäàåòñÿ ðàçëè÷íûìè àíàëèòè÷åñêèìè âûðà-
æåíèÿìè, íàïðèìåð
≤≤
≤≤
=
,ïðè
,ïðè
)(
)2(
1
)1(
1
1
bxcx
cxax
x
ϕ
ϕ
ϕ
òî èíòåãðàë ñïðàâà çàïèñûâàåòñÿ â âèäå ñóììû äâóõ èíòåãðàëîâ
.),(),(),(
)(
)(
)(
)(
)(
)(
2
)
2
(
1
2
)
1
(
1
2
1
∫∫∫∫∫∫
+=
x
x
b
c
x
x
c
a
x
x
b
a
d
y
y
x
f
dxd
y
y
x
f
dxd
y
y
x
f
dx
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
Àíàëîãè÷íî, åñëè îáëàñòü G îãðàíè÷åíà êðèâûìè x =
ψ
1
(y),
x =
ψ
2
(y), y = c, y = d, ïðè÷åì âñþäó íà [c, d] ôóíêöèè
ψ
1
(y)
è
ψ
2
(y) íåïðåðûâíû è
ψ
1
(y) ≤
ψ
2
(y) (ðèñ. 46), òî
.),(),(
)(
)(
2
1
∫∫∫ ∫
=
x
yG
d
c
dx
y
x
f
d
y
d
y
dx
y
x
f
ψ
ψ
(3.16)
Äâîéíîé èíòåãðàë, ïðåäñòàâëåííûé â âèäå (3.15) èëè (3.16),
íàçûâàåòñÿ òàêæå ïîâòîðíûì èíòåãðàëîì.
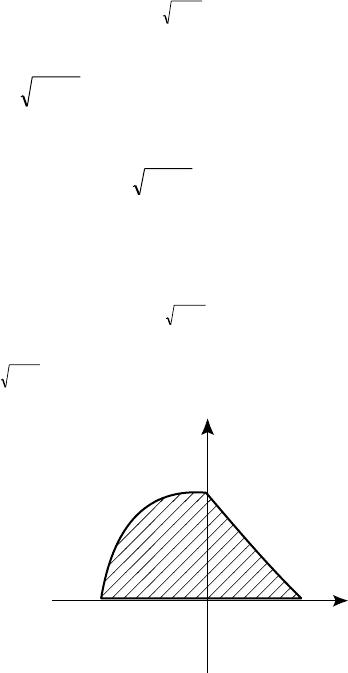
Ðèñ. 46
x
y
d
0
c
G
x =
φ
1
(y)
x =
φ
2
(y)
Ðèñ. 45
0 abx
G
y =
ϕ
1
(x)
y =
ϕ
2
(x)
y
176
Ïðèìåð 3.27. Èçìåíèòü ïîðÿäîê èíòåãðèðîâàíèÿ â ïîâòîðíîì
èíòåãðàëå
∫∫
−
−−
y
y
dx
y
x
f
d
y
1
1
1
0
2
.),(
Ñòðîèì îáëàñòü èíòåãðèðîâàíèÿ G ïî ïðåäåëàì èíòåãðèðîâà-
íèÿ:
2
1
1)(
yy −−=
ψ
,
ψ
2
(y) = 1 y, y = 0, y = 1 (ðèñ 47). Ñâåðõó
îáëàñòü G îãðàíè÷åíà êðèâîé
≤<−
≤≤−−
=
,10ïðè1
,01ïðè1
)(
2
2
xx
xx
X
ϕ
à ñíèçó ïðÿìîé y = 0. Ïîýòîìó èìååì
.),(),(),(
1
0
1
0
1
0
0
1
1
1
1
0
2
2
∫∫∫∫∫∫
−−
−
−
−−
+=
xx
y
y
d
y
y
x
f
dxd
y
y
x
f
dxd
y
y
x
f
d
y
Ïðèìåð 3.28. Âû÷èñëèòü äâîéíîé èíòåãðàë
∫∫
+
D
dydxyx
)2(
,
ãäå îáëàñòü èíòåãðèðîâàíèÿ îãðàíè÷åíà ïàðàáîëàìè y = x x
2
,
y = 1 x
2
è îñüþ Oy (ðèñ. 48).
Ðèñ. 47
x
2
+ y
2
= 1
1 0 1 x
y
1
x + y = 1
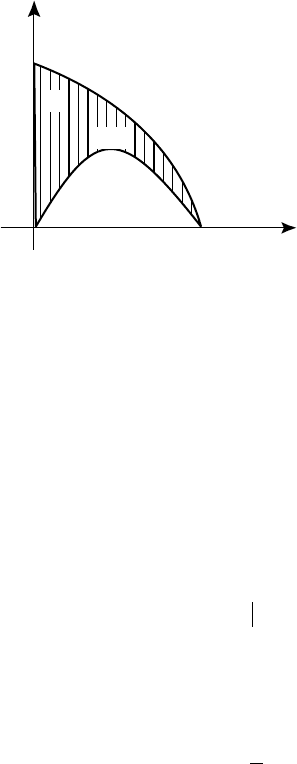
177
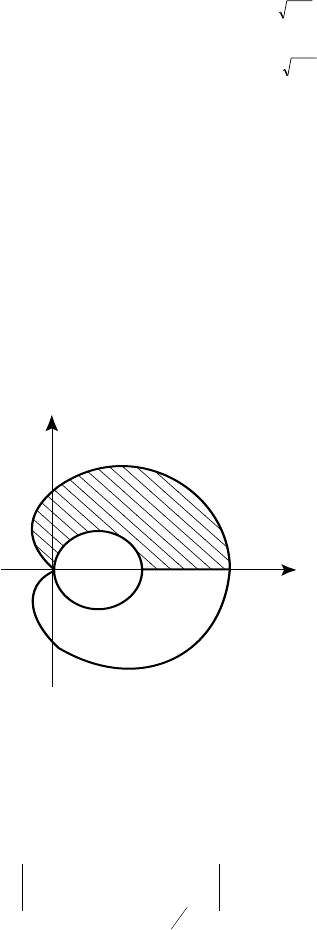
Ðåøåíèå. Ïàðàáîëû ïåðåñåêàþòñÿ â òî÷êå À (1; 0). Îáëàñòü èí-
òåãðèðîâàíèÿ D ÿâëÿåòñÿ ïðàâèëüíîé â íàïðàâëåíèè îñè Oy è îï-
ðåäåëÿåòñÿ íåðàâåíñòâàìè
0 ≤ x ≤ 1;
x x
2
≤ y ≤ 1 x
2
.
Ñëåäîâàòåëüíî,
∫∫∫∫
−
−
+=+
2
2
11
0
.)2()2(
x
xx
D
d
y
y
xdxd
y
dx
y
x
 ðåçóëüòàòå
.
3
2
)142(
])()()1()1([
)()2(
1
0
23
1
0
222222
1
1
0
2
2
2
∫
∫
∫∫∫
=++−=
=−−−−−+−=
=+=+
−
−
dxxxx
dxxxxxxxxx
dxyxydydxyx
x
xx
D
Ïðèìåð 3.29. Âûðàçèòü äâîéíîé èíòåãðàë ïî ôóíêöèè f(x; y) ïî
îáëàñòè D, îãðàíè÷åííîé ïàðàáîëîé y = 3 x
2
è ïðÿìîé y = 1, ÷åðåç
äâóêðàòíûå èíòåãðàëû ïðè ðàçëè÷íîì ïîðÿäêå èíòåãðèðîâàíèÿ.
Ðåøåíèå. Ðåøèâ ñèñòåìó óðàâíåíèé
−=
−=
1
3
2
y
xy
, íàéäåì òî÷êè
ïåðåñå÷åíèÿ ïàðàáîëû è ïðÿìîé. Ýòî áóäóò òî÷êè À (2; 1) è
Ðèñ. 48
0 x
y
y = x x
2
y = 1 x
2
D
(x, y)
A(1; 0)

178
 (2; 1). Âåðøèíà ïàðàáîëû íàõîäèòñÿ â òî÷êå Ñ (0; 3); îñü Îy
ÿâëÿåòñÿ îñüþ ñèììåòðèè ïàðàáîëû (ðèñ. 49).
Ðàññìîòðèì ñíà÷àëà ïîâòîðíûé èíòåãðàë ïî îáëàñòè D, èíòå-
ãðèðóÿ âî âíóòðåííåì èíòåãðàëå ïî y, à âî âíåøíåì èíòåãðàëå
ïî x. Äëÿ ýòîãî áóäåì ðàññìàòðèâàòü îáëàñòü D êàê çàêëþ÷åí-
íóþ â ïîëîñå ìåæäó ïðÿìûìè x = 2 è x = 2 (îáëàñòü D ïðîåê-
òèðóåòñÿ íà îñü Oõ â îòðåçîê [2; 2]). Îáëàñòü îãðàíè÷åíà
ñíèçó îòðåçêîì AB ñ óðàâíåíèåì y = 1(2 ≤ x ≤ 2), à ñâåðõó
äóãîé ïàðàáîëû y = 3x
2
(2 ≤ x ≤ 2). Ñëåäîâàòåëüíî, äâóêðàòíûé
èíòåãðàë áóäåò
∫∫
−
−−
2
3
1
2
2
.);(
x
d
y
y
x
f
dx
Èçìåíèì òåïåðü ïîðÿäîê èíòåãðèðîâàíèÿ, ò.å. áóäåì âî âíóò-
ðåííåì èíòåãðàëå èíòåãðèðîâàòü ïî õ, à âî âíåøíåì ïî y.
Äëÿ ýòîãî áóäåì ðàññìàòðèâàòü îáëàñòü D êàê çàêëþ÷åííóþ â
ïîëîñå ìåæäó ïðÿìûìè y = 1 è y = 3 (îáëàñòü D ïðîåêòèðóåòñÿ
íà îñü Oy â îòðåçîê [1; 3]). Îáëàñòü îãðàíè÷åíà ñëåâà äóãîé
ïàðàáîëû
yx −−= 3
(1 ≤ y ≤ 3), à ñïðàâà äóãîé ïàðàáîëû
yx −= 3
(1 ≤ y ≤ 3). Ýòè óðàâíåíèÿ ïîëó÷àþòñÿ, åñëè óðàâíå-
íèå y = 3 x
2
ðàçðåøèòü îòíîñèòåëüíî x. Ñëåäîâàòåëüíî, òåïåðü
äâóêðàòíûé èíòåãðàë áóäåò
∫∫
−
−−
−
y
y
dxyxfdy
3
3
3
1
.);(
Ðèñ. 49
A
1
y
C
B
x
2
2
179
Èòàê,
∫∫∫∫∫ ∫
−
−−
−
−
−−
==
y
y
x
D
dx
y
x
f
d
y
d
y
y
x
f
dxd
y
dx
y
x
f
3
3
3
1
3
1)(
2
2
.);();();(
2
Ïëîùàäü S ïëîñêîé îáëàñòè G âûðàæàåòñÿ, â çàâèñèìîñòè îò
ðàññìàòðèâàåìîé ñèñòåìû êîîðäèíàò, ñëåäóþùèìè èíòåãðàëàìè:
∫∫
=
G
d
y
dxS
(3.17)
â äåêàðòîâûõ ïðÿìîóãîëüíûõ êîîðäèíàòàõ, à â ïîëÿðíûõ êîîð-
äèíàòàõ x = r cos
ϕ
, y = r sin
ϕ
èìååì
.
ϕ
ddrrS
G
∫∫
=
(3.18)
Ïðèìåð 3.30. Íàéòè ïëîùàäü ôèãóðû, îãðàíè÷åííîé êðèâûìè
r = a (1 + cos ϕ) è r = a cosϕ (a > 0).
 ïëîñêîñòè Oxy ôèãóðà ïîêàçàíà íà ðèñ. 50.
Âû÷èñëèì ïî ôîðìóëå (3.18) ïëîùàäü âåðõíåé ÷àñòè è óäâîèì:
=
+
+
+
=
=+==
∫∫
∫∫∫∫ ∫∫
++
ϕ
ϕ
ϕ
ϕ
ϕ
ϕϕϕ
π
π
π
ϕ
π
π
ϕ
ϕ
π
d
a
rd
a
a
r
drrddrrdddrrS
a
G
a
a
2
2
2/
0
2
)cos1(
02/
)cos1(
cos
2/
0
0
)cos1(
cos
)cos1(
222
Ðèñ. 50
a
r = a (1 + cos
ϕ
)
x2a
y
r = a cos
ϕ
180
.
4
5
2sin
4
1
sin2
2
3
0
2/
)sin2(
)coscos21()cos21(
2
2/
22
2/
22
2/
0
2
aaa
dada
πϕϕ
ϕ
π
ϕϕ
ϕϕϕϕϕ
π
π
π
π
π
=
++++=
=++++=
∫∫
Îáúåì V öèëèíäðà, îãðàíè÷åííîãî ñâåðõó íåïðåðûâíîé ïî-
âåðõíîñòüþ z = f (x, y), ñíèçó ïëîñêîñòüþ z = 0 è ñ áîêîâ ïðÿìîé
öèëèíäðè÷åñêîé ïîâåðõíîñòüþ, âûðåçàþùåé íà ïëîñêîñòè Oxy îá-
ëàñòü G, âûðàæàåòñÿ èíòåãðàëîì
∫∫
=
G
d
y
dx
y
x
f
V
),(
(3.19)
(ôóíêöèÿ f (x, y) ≥ 0 îäíîçíà÷íà â îáëàñòè G).
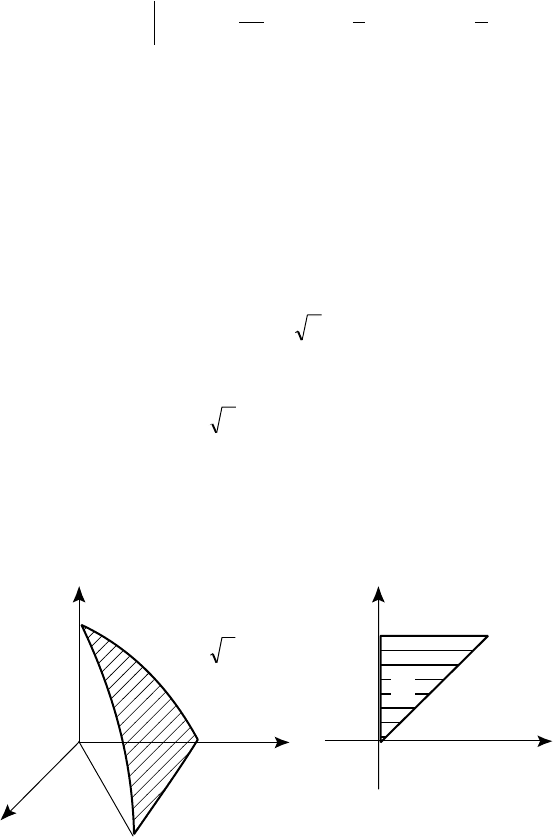
Ïðèìåð 3.31. Âû÷èñëèòü îáúåì òåëà, îãðàíè÷åííîãî ïîâåðõ-
íîñòÿìè z = 0, x = 0, y = x, z = 1 y
y
.
Ðåøåíèå. Ïîñòðîèì ÷åðòåæ, íà êîòîðîì èçîáðàçèì òåëî, îãðà-
íè÷åííîå óêàçàííûìè ïîâåðõíîñòÿìè (ðèñ. 51 à). Îáúåì òåëà
∫∫
=
D
d
y
dxzV
, ãäå
yyz −=1
óðàâíåíèå ïîâåðõíîñòè, îãðàíè-
÷èâàþùåé òåëî ñâåðõó, à D îáëàñòü èíòåãðèðîâàíèÿ, ïðåäñòàâ-
ëÿþùàÿ ñîáîé òðåóãîëüíèê â ïëîñêîñòè xOy, îãðàíè÷åííûé ïðÿ-
ìûìè x = 0, y = x è y = 1, ÿâëÿþùèìèñÿ ëèíèÿìè ïåðåñå÷åíèÿ
Ðèñ. 51
x
y
x
y
a)
z
y = x
á)
y = 1
0
D
0
1
D
y = 1
y = x
yyz −=1
(1; 1)
