Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
Подождите немного. Документ загружается.


161
Îïðåäåëåííûì èíòåãðàëîì îò ôóíêöèè f (x) ïî [a, b] íàçûâàåò-
ñÿ âåëè÷èíà
.))((lim)(
1
1
0||max
1
−
=
→−
∞→
−=
∑
∫
−
iii
n
i
xx
n
b
a
xx
f
dxx
f
ii
ξ
(3.4)
Ñâîéñòâà îïðåäåëåííîãî èíòåãðàëà:
.)()()(.5
.0)(òî,0)(Åñëè.4
.)()(.3
.)()()]()([.2
.)()(.1
∫∫∫
∫
∫∫
∫∫∫
∫∫
+=
≥≥
=
±=±
−=
b
c
c
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
a
b
b
a
dxx
f
dxx
f
dxx
f
dxx
f
x
f
dxx
f
kdxx
f
k
dxxgdxx
f
dxxgx
f
dxx
f
dxx
f
3.2.2. Âû÷èñëåíèå îïðåäåëåííîãî èíòåãðàëà
Îïðåäåëåííûé èíòåãðàë ñâÿçàí ñ íåîïðåäåëåííûì èíòåãðàëîì
ïî ôîðìóëå:
,)()(
a
b
b
a
xFdxx
f
=
∫
(3.5)
ãäå F(x) ïðîèçâîëüíàÿ ïåðâîîáðàçíàÿ ôóíêöèÿ f (x).
).()()( aFbFxF
a
b
−=
(3.6)
Ôîðìóëà (3.5) íàçûâàåòñÿ ôîðìóëîé Íüþòîíà-Ëåéáíèöà.
162
Ïðèìåð 3.12.
.
3
7
3
1
3
2
3
3
1
2
3
2
1
2
=−==
∫
x
dxx
Çàìåíà ïåðåìåííîé â îïðåäåëåííîì èíòåãðàëå îòëè÷àåòñÿ îò
çàìåíû ïåðåìåííîé â íåîïðåäåëåííîì èíòåãðàëå òåì, ÷òî:
1) íåîáõîäèìî èçìåíèòü ïðåäåëû èíòåãðèðîâàíèÿ;
2) âîçâðàùàòüñÿ ê ïåðâîíà÷àëüíîé ïåðåìåííîé íå íàäî.
Ïðèìåð 3.13. Ïîëüçóÿñü ôîðìóëîé Íüþòîíà-Ëåéáíèöà, âû÷èñ-
ëèòü îïðåäåëåííûé èíòåãðàë
∫
+
8
3
.
1
dx
x
x
Ðåøåíèå. ×òîáû èçáàâèòüñÿ îò èððàöèîíàëüíîñòè, ñäåëàåì
ïîäñòàíîâêó 1 + õ = t
2
. Òîãäà
.
3
32
2
3
8
3
3
27
2
3
2
)1(2
2)1(
38
23
2
1
1
2
3
3
3
2
2
3
2
2
8
3
2
=
+−−=
−=
=−=
−
=
=→=
=→=
=
=+
=
+
∫∫∫
t
t
dtt
t
tdtt
tx
tx
tdtdx
tx
x
xdx
Ôîðìóëà èíòåãðèðîâàíèÿ ïî ÷àñòÿì â îïðåäåëåííîì èíòåãðàëå:
∫∫
−=
b
a
b
a
a
b
xduxvxvxuxdvxu
),()()()()()(
(3.7)
ãäå
a
b
xvxu
)()(
âû÷èñëÿåòñÿ ïî ôîðìóëå (3.6).
3.2.3. Ïðèëîæåíèÿ îïðåäåëåííîãî èíòåãðàëà
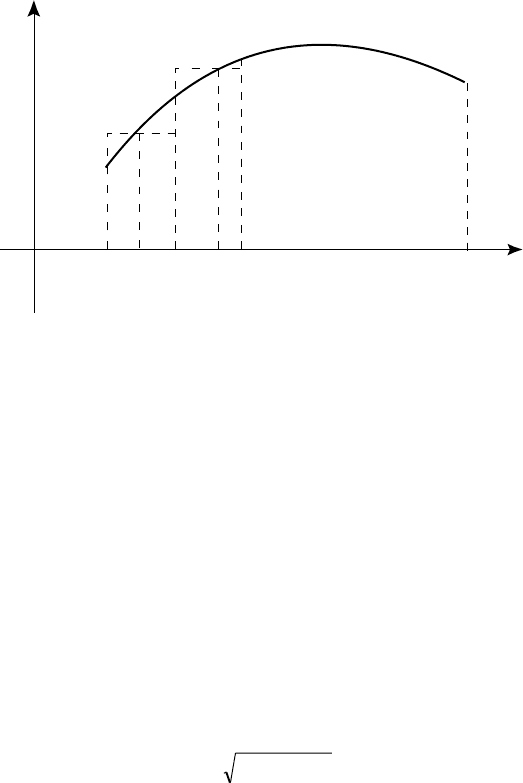
Ãåîìåòðè÷åñêèé ñìûñë îïðåäåëåííîãî èíòåãðàëà (3.4) ñîñòîèò
â òîì, ÷òî åñëè ãðàôèê ôóíêöèè y = f (x) îãðàíè÷èâàåò êðèâîëè-
íåéíóþ òðàïåöèþ Φ = {(x, y) | a ≤ x ≤ b, 0 ≤ y ≤ f (x)}, òî åãî âåëè÷è-
íà ðàâíà ïëîùàäè ýòîé òðàïåöèè. ×òîáû óáåäèòüñÿ â ýòîì, äîñòà-
163
òî÷íî ðàññìîòðåòü ðèñ. 38 è çàìåòèòü, ÷òî ïëîùàäü êðèâîëèíåé-
íîé òðàïåöèè:
).()(
1
1
−
=
−≈
∑
ii
n
i
i
xx
f
S
ξ
Ýòî ðàâåíñòâî òåì òî÷íåå, ÷åì áîëüøå n. Ïîýòîìó òî÷íîå çíà-
÷åíèå:
∫
∑
=−=
−
=
→−
∞→
−
b
a
iii
n
i
xx
n
dxx
f
xx
f
S
ii
.)())((lim
1
1
0||max
1
ξ
(3.8)
Îáúåì òåëà, îáðàçîâàííîãî âðàùåíèåì êðèâîëèíåéíîé òðà-
ïåöèè âîêðóã îñè Îõ, âû÷èñëÿåòñÿ ïî ôîðìóëå:
∫
=
b
a
dxx
f
V
,)]([
2
π
(3.9)
à äëèíà äóãè ëèíèè y = f(x), çàêëþ÷åííîé ìåæäó òî÷êàìè ñ àáñ-
öèññàìè à è b, âû÷èñëÿåòñÿ ïî ôîðìóëå:
.))((1
2
dxxfL
b
a
∫
′
+=
(3.10)
Ðèñ. 38
x
n
= b
y
= f(x)
y
0 õ
0
=a
ξ
1
x
1
ξ
2
x
2
164
Ïðèìåð 3.14. Âû÷èñëèòü ïëîùàäü ôèãóðû, îãðàíè÷åííîé ëè-
íèÿìè y = x + 2,
.62
2
2
+−=
x
xy
Ñäåëàòü ÷åðòåæ.
Íàõîäèì òî÷êè ïåðåñå÷åíèÿ çàäàííûõ ëèíèé. Äëÿ ýòîãî ðåøà-
åì ñèñòåìó óðàâíåíèé:
+−=
+=
.6
2
2
,2
2
x
xy
xy
Äëÿ íàõîæäåíèÿ àáñöèññ òî÷åê ïåðåñå÷åíèÿ çàäàííûõ ëèíèé ðå-
øàåì óðàâíåíèå:
6
2
22
2
+−=+
x
xx
èëè õ
2
2õ 8 = 0.
Íàõîäèì: õ
1
= 2, õ
2
= 4.
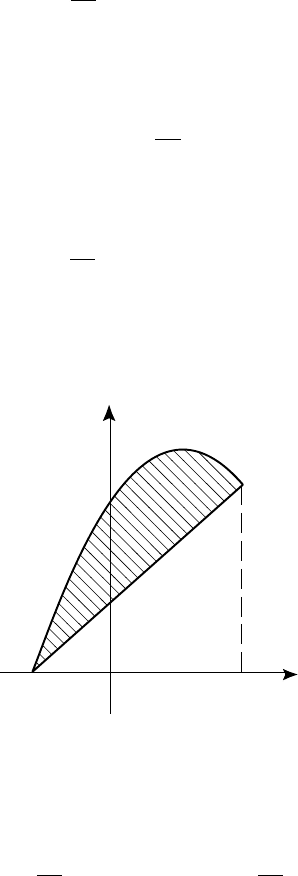
Èòàê, äàííûå ëèíèè, ïðåäñòàâëÿþùèå ñîáîé ïàðàáîëó è ïðÿ-
ìóþ, ïåðåñåêàþòñÿ â òî÷êàõ À(2; 0), Â(4; 6) (ðèñ. 39).
Ýòè ëèíèè îáðàçóþò çàìêíóòóþ ôèãóðó, ïëîùàäü êîòîðîé âû-
÷èñëÿåì ïî óêàçàííîé âûøå ôîðìóëå:
∫∫
−−
+−=
−−+−=
4
2
2
4
2
2
.4
2
26
2
2
dx
x
xdxx
x
xS
Ðèñ. 39
y
2 4
x
B
A
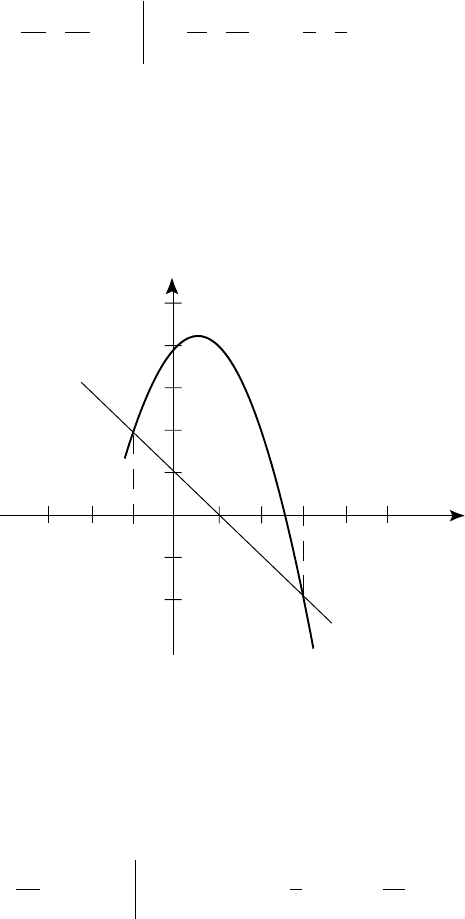
165
Ïîñëåäíèé èíòåãðàë íàõîäèì ïî ôîðìóëå Íüþòîíà-Ëåéáíèöà:
)åä. êâ.(188
6
8
2
4
16
6
64
2
16
4
62
2
4
32
=+−−+−=
+−=
−
x
xx
S
Ïðèìåð 3.15. Âû÷èñëèòü ïëîùàäü ôèãóðû, îãðàíè÷åííîé ëè-
íèÿìè y = x
2
+ x + 4 è y = x
+ 1.
Íàéäåì òî÷êè ïåðåñå÷åíèÿ ëèíèé y = x
2
+ x + 4, y = x + 1,
ïðèðàâíèâàÿ îðäèíàòû ëèíèé: x
2
+ x + 4 = x + 1 èëè x
2
2x 3 = 0.
Íàõîäèì êîðíè õ
1
= 1, õ
2
= 3 è ñîîòâåòñòâóþùèå èì îðäèíà-
òû y
1
= 2, y
2
= 2 (ðèñ. 40).
Ïî ôîðìóëå ïëîùàäè ôèãóðû ïîëó÷èì:
()
).åä. êâ.(
3
32
31
3
1
)999(3
3
)32()1()4(
1
3
2
3
3
1
2
3
1
2
=
−+−++=
++−=
=++−=+−−++−=
−
−−
∫∫
xx
x
dxxxdxxxxS
Ðèñ. 40
y
5
4
3
2
1
1
2
2 1
0
1 2 3 4
x
y = x
2
+ x + 4
y = x + 1
166
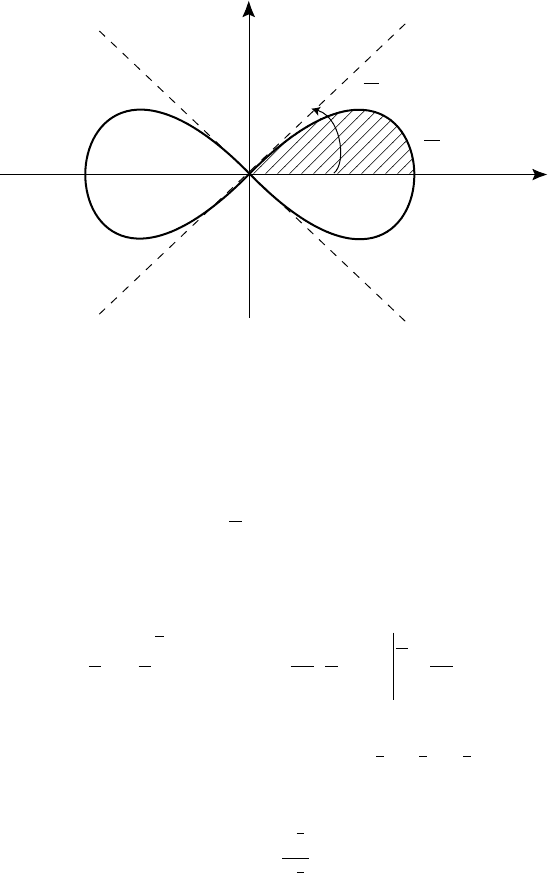
Ïðèìåð 3.16. Íàéòè ïëîùàäü, çàêëþ÷åííóþ âíóòðè ëåìíèñêà-
òû Áåðíóëëè r
2
= a
2
cos 2
ϕ
(ðèñ. 41).
 ïîëÿðíîé ñèñòåìå êîîðäèíàò ïëîùàäü ôèãóðû, îãðàíè÷åí-
íîé äóãîé êðèâîé r = f(
ϕ
) è äâóìÿ ïîëÿðíûìè ðàäèóñàìè
ϕ
1
=
α
è
ϕ
2
=
β
, âûðàçèòñÿ èíòåãðàëîì
.)]([
2
1
2
ϕϕ
β
α
dfS
∫
=
 ñèëó ñèììåòðèè êðèâîé (ðèñ. 41) îïðåäåëÿåì ñíà÷àëà îäíó
÷åòâåðòóþ èñêîìîé ïëîùàäè:
.
4
2sin
2
1
2
2cos
2
1
4
1
2
0
4
2
0
2
4
aa
daS =⋅==
∫
π
ϕϕϕ
π
Îòñþäà S = a
2
.
Ïðèìåð 3.17. Íàéòè äëèíó àñòðîèäû
3
2
3
2
3
2
ayx =+
(ðèñ. 42).
Äèôôåðåíöèðóÿ óðàâíåíèå àñòðîèäû, ïîëó÷èì:
.
3
1
3
1
x
y
y −=
′
Ðèñ. 41
4
S
y
x
4
π
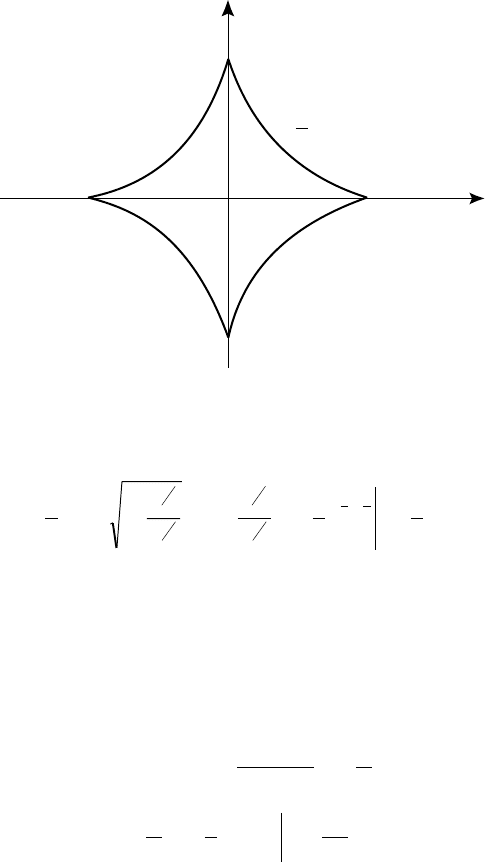
167
Ïîýòîìó äëÿ äëèíû äóãè îäíîé ÷åòâåðòè àñòðîèäû èìååì:
.
2
3
2
3
1
4
1
0
00
3
2
3
1
3
1
3
1
3
2
3
2
axadx
x
a
dx
x
y
L
a
aa
===+=
∫∫
Îòñþäà L = 6a.
Ïðèìåð 3.18. Âû÷èñëèòü îáúåì òåëà, îáðàçîâàííîãî âðàùåíè-
åì ôèãóðû, îãðàíè÷åííîé îäíîé ïîëóâîëíîé ñèíóñîèäû y = sin x
âîêðóã îñè Îõ.
Ðåøåíèå.
.
2
2sin
2
1
2
)2cos1(
22
2cos1
sin
2
0
000
2
0
2
ππ
π
πππ
π
ππππ
=
−=
=−=
−
===
∫∫∫∫
xx
dxxdx
x
dxxdxyV
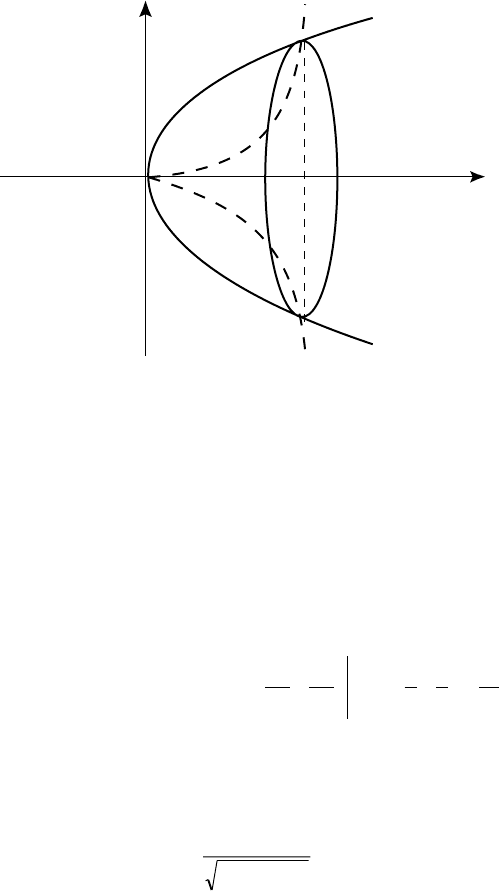
Ïðèìåð 3.19. Âû÷èñëèòü îáúåì òåëà, ïîëó÷åííîãî âðàùåíèåì
âîêðóã îñè Îõ ôèãóðû, îãðàíè÷åííîé ïàðàáîëàìè y = x
2
è õ = ó
2
(ðèñ. 43).
Ðèñ. 42
0
x
y
à
L
4
1
à
168
Ðèñ. 43
0 À
y
x
y = x
2
x = y
2
C
D
B(1; 1)
Ðåøåíèå. Ðåøèâ ñèñòåìó óðàâíåíèé
=++−=−==
=
,0)1)(1(,0,,
,
2442
2
xxxxxxxxxy
xy
ïîëó÷èì x
1
= 0, x
2
= 1, ó
1
= 0, ó
2
= 1, îòêóäà òî÷êè ïåðåñå÷åíèÿ
êðèâûõ Î(0; 0), Â(1; 1). Êàê âèäíî (ðèñ. 43), èñêîìûé îáúåì òåëà
âðàùåíèÿ ðàâåí ðàçíîñòè äâóõ îáúåìîâ, îáðàçîâàííûõ âðàùåíè-
åì âîêðóã îñè Îõ êðèâîëèíåéíûõ òðàïåöèé OCBA è ODÂA:
.
10
3
5
1
2
1
52
0
1
52
1
0
4
1
0
21
πππππ
=
−=
−=−=−=
∫∫
xx
dxxdxxVVV
3.3. Ôóíêöèè íåñêîëüêèõ ïåðåìåííûõ
Ïðèìåð 3.20. Íàéòè îáëàñòü ñóùåñòâîâàíèÿ ôóíêöèè
22
4
1
yx
z
−−
=
Ðåøåíèå. Ôóíêöèÿ èìååò äåéñòâèòåëüíûå çíà÷åíèÿ, åñëè 4 x
2
y
2
> 0 èëè x
2
+ y
2
< 4. Ïîñëåäíåìó íåðàâåíñòâó óäîâëåòâîðÿþò
êîîðäèíàòû òî÷åê, ëåæàùèõ âíóòðè îêðóæíîñòè ðàäèóñà 2 ñ öåí-

169
Ïðèìåð 3.21. Íàéòè òî÷êè ðàçðûâà ôóíêöèè
.
1
2
yx
xy
z
−
+
=
Ðåøåíèå. Ôóíêöèÿ ïîòåðÿåò ñìûñë, åñëè çíàìåíàòåëü îáðàòèòñÿ
â íóëü. Íî x
2
y = 0 èëè ó = x
2
óðàâíåíèå ïàðàáîëû. Ñëåäîâà-
òåëüíî, äàííàÿ ôóíêöèÿ èìååò ëèíèåé ðàçðûâà ïàðàáîëó ó = x
2
.
Ïðèìåð 3.22. Íàéòè ÷àñòíûå ïðîèçâîäíûå ôóíêöèè z = f (x; y):
a) z = f (x; y) = x
5
2xy
2
+ 3xy x.
Ðàññìàòðèâàÿ y êàê ïîñòîÿííóþ âåëè÷èíó, ïîëó÷èì
.1325)32(
2425
−+−=
′
−+−=
∂
∂
yyxxxyxyx
x
z
x
Ïîëàãàÿ òåïåðü õ ïîñòîÿííîé âåëè÷èíîé, ïîëó÷èì
.34)32(
25
xxyxxyxyx
y
z
y
+=
′
−+−=
∂
∂
á) z = ln(x
3
+ y
3
).
Ðàññìàòðèâàÿ ó êàê ïîñòîÿííóþ âåëè÷èíó, ïîëó÷èì
.
3
)(
1
33
2
33
33
yx
x
yx
yx
x
z
x
+
=
′
+⋅
+
=
∂
∂
òðîì â íà÷àëå êîîðäèíàò. Îáëàñòü ñóùåñòâîâàíèÿ ôóíêöèè åñòü
ìíîæåñòâî òî÷åê âíóòðè ýòîãî êðóãà (ðèñ. 44).
Ðèñ. 44
y
x
2

170
Ïîëàãàÿ òåïåðü x = const, íàõîäèì
.
3
)(
1
33
2
33
33
yx
y
yx
yx
y
z
y
+
=
′
+⋅
+
=
∂
∂
Ïîëíûé äèôôåðåíöèàë ôóíêöèè z = f (x; y) îïðåäåëÿåòñÿ ôîð-
ìóëîé
.dy
y
z
dx
x
z
dz
∂
∂
+
∂
∂
=
Ïðèìåð 3.23. Íàéòè ïîëíûé äèôôåðåíöèàë ôóíêöèè
z = 3x
2
y
3
2x
2
y ó.
Íàõîäèì ïðåæäå âñåãî ÷àñòíûå ïðîèçâîäíûå
.129;46
2223
−−=
∂
∂
−=
∂
∂
xyx
y
z
xyxy
õ
z
Òîãäà ïîëíûé äèôôåðåíöèàë ðàâåí
dz = 2xy(3y
2
2)dx + (9x
2
y
2
2x
2
1)dó.
Ïðèìåð 3.24. Íàéòè ÷àñòíûå ïðîèçâîäíûå âòîðîãî ïîðÿäêà
ôóíêöèè z = cosx
5
y
2
.
Ñíà÷àëà íàõîäèì ÷àñòíûå ïðîèçâîäíûå ïåðâîãî ïîðÿäêà.
,5sin)(sin
24252525
yxyxyxyx
õ
z
x
⋅=
′
=
∂
∂
.2sin)(sin
5252525
yxyxyxyx
y
z
y
⋅=
′
=
∂
∂
Òîãäà
.cos25sin20
)(cos5sin20
)(sin5sin)5()sin5(
25482523
2525242523
252425242524
2
2
yxyxyxyx
yxyxyxyxyx
yxyxyxyxyxyx
x
z
x
xxx
=
=
′
⋅=
=
′
−⋅
′
=
′
⋅=
∂
∂
