Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
Подождите немного. Документ загружается.

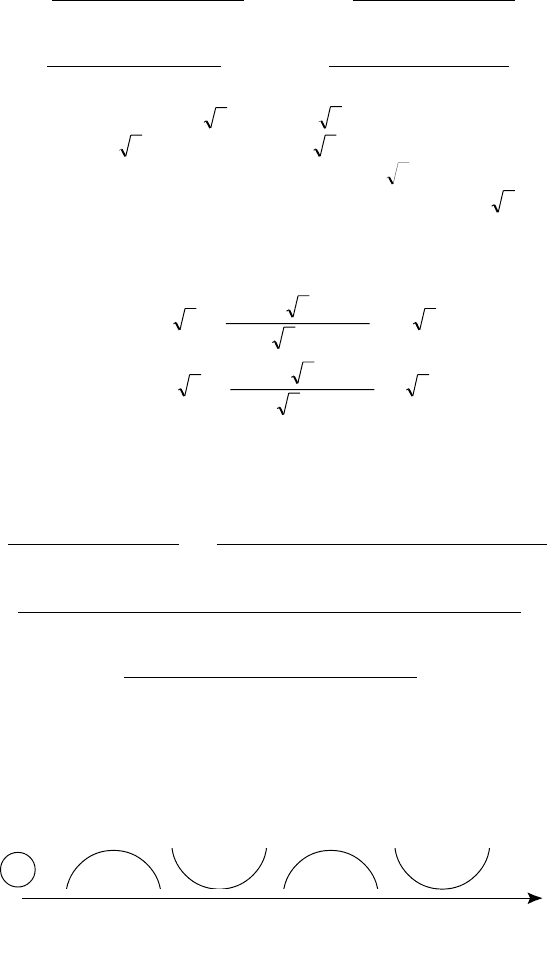
141
x
•
׿׿
1 3 5
y″
.0
)4)38((
)3868()38(
)8(;0
)4)34((
)3464()34(
)4(
,0
)4)30((
)3060()30(
)0(;0
)4)31((
)3)1(61()31(
)1(
22
22
22
22
22
2
22
2
>
−−
−⋅−⋅−
=
′
<
−−
−⋅−−
=
′
<
−−
−⋅−−
=
′
>
−−−
−−⋅−−−
=−
′
yy
yy
 èíòåðâàëàõ
]323;( −−∞
è
);323[ ∞++
ôóíêöèÿ âîçðàñòàåò,
â èíòåðâàëå
]323;5()5;1()1;323[ +∪∪−
ôóíêöèÿ óáûâàåò.
Òàê êàê ïðè ïåðåõîäå ÷åðåç òî÷êó
323 −=x
ïðîèçâîäíàÿ ìå-
íÿåò çíàê ñ «+» íà «», òî ýòî òî÷êà max. Òî÷êà
323 +=x
áóäåò
òî÷êîé min, òàê êàê ïðè ïåðåõîäå ÷åðåç íåå ïðîèçâîäíàÿ ìåíÿåò
çíàê ñ «» íà «+». Íàéäåì:
.33
4)3323(
)3323(
)323(
,33
4)3323(
)3323(
)323(
2
3
min
2
3
max
=
−−−
−+
=+
−=
−−−
−−
=−
y
y
7. Äëÿ îòûñêàíèÿ èíòåðâàëîâ âûïóêëîñòè è âîãíóòîñòè è òî-
÷åê ïåðåãèáà íàéäåì âòîðóþ ïðîèçâîäíóþ:
.
)4)3((
)216)(4)3(()3(8
)4
)3(2)4)3((2)36()3()4)3((
)3((
))62()3()36)(3(2(
)4)3((
)36()3(
42
22
4
22222
2
22
22
22
−−
+−−−⋅−
=
=
−
−⋅−−⋅−−−−−−
→
→
−
−−+−−−
=
′
−−
−−−
=
′′
x
xxxx
õxxxxx
x
xxxxx
x
xxx
y
Èç óñëîâèÿ y″ = 0 èìååì õ 3 = 0 èëè õ = 3. Óñëîâèþ y″ = ∞
ñîîòâåòñòâóåò õ = 1 è õ = 5 (òî÷êè ðàçðûâà ôóíêöèè). Íàíîñèì
ýòè òðè òî÷êè íà ÷èñëîâóþ îñü è èññëåäóåì çíàê âòîðîé ïðîèç-
âîäíîé íà êàæäîì èç èíòåðâàëîâ:
•
•
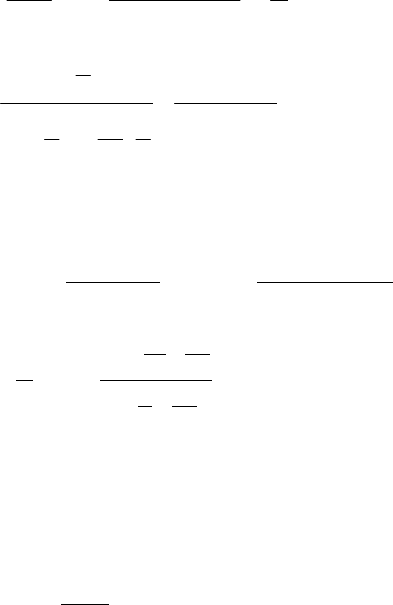
142
 èíòåðâàëàõ (∞; 1) è [3; 5) ãðàôèê ôóíêöèè âûïóêëûé, à â
èíòåðâàëàõ (1; 3] è (5; ∞) âîãíóòûé.  òî÷êå õ = 3 ãðàôèê ôóíê-
öèè ìåíÿåò íàïðàâëåíèå âûïóêëîñòè è òàê êàê f(3) = 0, òî òî÷êà
(3; 0) åñòü òî÷êà ïåðåãèáà.
8. Íàêëîííóþ àñèìïòîòó èùåì â âèäå:
y = kx + b,
ãäå
1
)0)01((
)01(
43
1
3
1
lim
)4)3((
)3(
lim
)(
lim
2
3
2
2
3
2
3
=
−−
−
=
−
−
−
=
=
∞
∞
=
⋅−−
−
==
∞→
∞→∞→
x
x
x
x
x
xx
x
x
xf
k
x
xx
è
.3
56
1
2722
3
lim
56
27223
lim
4)3(
)3(
lim))((lim
2
2
2
2
2
3
−=
+−
−+−
=
∞
∞
=
=
+−
−+−
=
−
−−
−
=−=
∞→
∞→∞→∞→
x
x
x
x
xx
xx
x
x
x
kxxfb
x
xxx
Ñëåäîâàòåëüíî, íàêëîííàÿ àñèìïòîòà èìååò âèä: ó = õ 3.
9. Ñòðîèì ãðàôèê ôóíêöèè (ðèñ. 37).
Çàìå÷àíèå. Ââîäÿ íîâóþ ïåðåìåííóþ t = x 3, ìîæíî ðàñ-
ñìàòðèâàòü ôóíêöèþ
,
4
2
3
−
=
t
t
y
èññëåäîâàòü è ïîñòðîèòü åå ãðà-
ôèê, à çàòåì ïåðåíåñòè îñü Îf(x) íà 3 åä. âëåâî è âìåñòî îñè Ît
íàïèñàòü îñü Îõ.
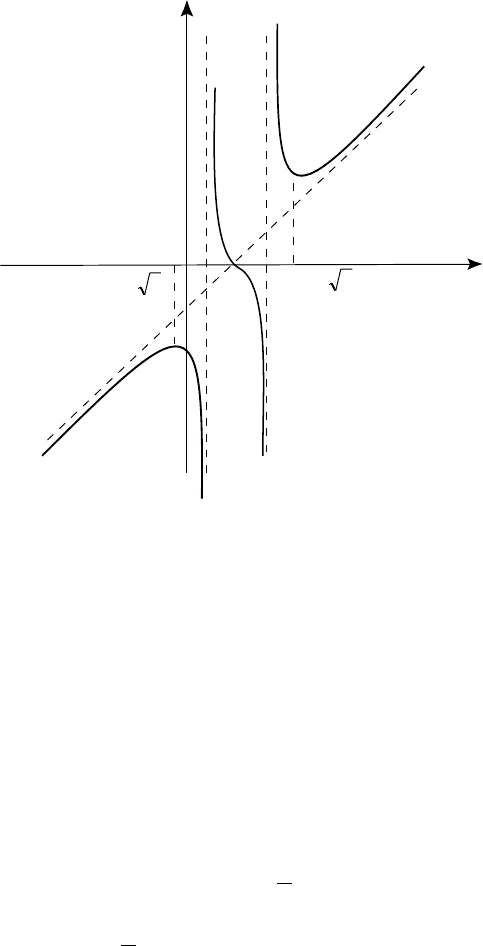
143
3.5. Ïðèáëèæåííîå ðåøåíèå àëãåáðàè÷åñêèõ óðàâíåíèé
3.5.1. Îòäåëèòü ïîëîæèòåëüíûé êîðåíü óðàâíåíèÿ 4x cos 2x = 0
è ðåøèòü åãî ïðèáëèæåííî ñ òî÷íîñòüþ
ε
= 0,01:
à) ìåòîäîì äåëåíèÿ îòðåçêà ïîïàëàì;
á) ìåòîäîì Íüþòîíà (ìåòîä êàñàòåëüíûõ).
Ïðèìå÷àíèå. Ìîæíî ñ÷èòàòü, ÷òî òî÷íîñòü
ε
äîñòèãíóòà, åñëè
ðàçíîñòü ìåæäó ñîñåäíèìè ïðèáëèæåíèÿìè x
k + 1
è x
k
óäîâëåòâî-
ðÿåò íåðàâåíñòâó | x
k + 1
x
k
| <
ε
.
à) Ïóñòü äàíî óðàâíåíèå
f(x) = 4x cos 2x = 0,
ãäå ôóíêöèÿ f (x) íåïðåðûâíà íà
4
;0
π
(ôóíêöèÿ f (x) èçìåíÿåòñÿ
îò 1 äî 0) è
.0)1()0(
4
<−=⋅−=⋅
ππ
π
ff
Ðèñ. 37
f(x)
32
3
13 5
x
0
323+

144
Äåëèì
4
;0
π
ïîïîëàì è âûáèðàåì òó èç ïîëîâèí
8
;0
π
èëè
4
;
8
ππ
, íà êîíöàõ êîòîðîé ôóíêöèÿ f(x) èìååò ïðîòèâîïîëîæíûå
çíàêè è, òàê êàê
,0864,0)1()0(
8
<⋅−=⋅
π
ff
òî âûáèðàåì
8
;0
π
è ò.ä.
Ïîñëåäîâàòåëüíî èìååì:
.0094,0
256
37
cos
512
37
4
512
37
:
256
19
;
128
9
;0395,0
128
19
cos
256
19
4
256
19
:
64
5
;
128
9
;0104,0
64
9
cos
128
9
4
128
9
:
64
5
;
16
;0998,0
32
5
cos
64
5
4
64
5
:
32
3
;
16
;337,0
16
3
cos
32
3
4
32
3
:
8
;
16
;138,0
8
cos
16
4
16
:
8
;0
;
2
cos
4
4
4
;10cos04)0(:
4
;0
=−⋅=
=−⋅=
=−⋅=
=−⋅=
=−⋅=
−=−⋅=
=−⋅=
−=−⋅=
πππππ
πππππ
πππππ
πππππ
πππππ
ππππ
π
ππππ
f
f
f
f
f
f
ff
Òàê êàê
,01,00061,0
256
19
512
37
=<=
−
ε
ππ
òî ìîæíî ïðèíÿòü
.227,0
512
37
=
=
π
x
á) Îòäåëÿåì ïîëîæèòåëüíûé êîðåíü óðàâíåíèÿ
f(x) = 4x cos 2x = 0
ìåòîäîì Íüþòîíà.
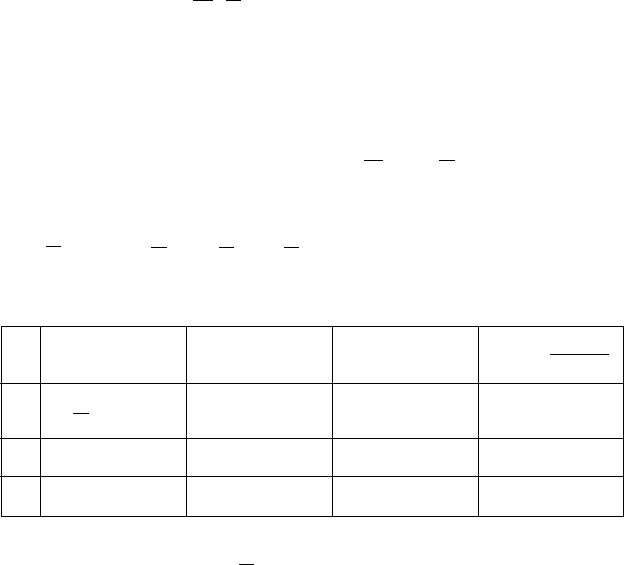
145
Ó÷èòûâàÿ ïðåäûäóùåå ðåøåíèå, çàêëþ÷àåì, ÷òî èñêîìûé êî-
ðåíü íàõîäèòñÿ íà
8
;
16
ππ
, èìååì:
f ′ (x) = 4 + 2sin 2x
f ″ (x) = 4cos 2x.
Îòñþäà f ′ (x) > 0 è f ″ (x) > 0 ïðè
.
816
ππ
≤≤ x
Òàê êàê äîëæíî
áûòü f (x
0
) · f ″ (x
0
) > 0, òî çà íà÷àëüíîå ïðèáëèæåíèå ïðèíèìàåì
,
8
0
π
=x
èáî
.0864,0cos4
488
>=−⋅=
πππ
f
Âû÷èñëåíèå ïðîèçâî-
äèì ïî ñëåäóþùåé ñõåìå:
nx
n
f (x
n
) f ′ (x
n
)
0 0,864 5,414 0,159
1 0,234 0,044 4,902 0,009
2 0,225 0,0004 4,870 0,00008
Íàõîäèì
,414,5786,0sin24)(
8
0
=+=
′
=
′
π
fxf
çàòåì h
0
.
Âû÷èñëÿåì
x
1
= x
0
+ h = 0,393 0,159,
f (x
1
) = f (0,234) = 4 · 0,234 cos 0,468 = 0,044,
çàòåì f ′(x
1
) è h
1
. Äàëåå îïðåäåëÿåì
x
2
= x
1
+ h = 0,225,
f (x
2
) è f ′ (x
2
). Òàê êàê | x
2
x
1
| = | 0,225 0,234 | = 0,009 <
ε
= 0,01,
òî çà ïîëîæèòåëüíûé êîðåíü ïðèíèìàåì 0,225.
)(
)(
n
n
n
xf
xf
h
′
−=
393,0
8
=
π

146
Ðàçäåë 3
ÈÍÒÅÃÐÀËÜÍÎÅ ÈÑ×ÈÑËÅÍÈÅ
3.1. Íåîïðåäåëåííûé èíòåãðàë
3.1.1. Ïåðâîîáðàçíàÿ ôóíêöèÿ
è íåîïðåäåëåííûé èíòåãðàë
 äèôôåðåíöèàëüíîì èñ÷èñëåíèè ïî çàäàííîé ôóíêöèè F(x)
íàõîäÿò åå ïðîèçâîäíóþ f (x) = F′ (x). Íà ïðàêòèêå ÷àñòî ïðèõî-
äèòñÿ ðåøàòü îáðàòíóþ çàäà÷ó: òðåáóåòñÿ âîññòàíîâèòü ôóíêöèþ
F(x), çíàÿ åå ïðîèçâîäíóþ f (x). Ôóíêöèþ F(x) â ýòîì ñëó÷àå íàçû-
âàþò ïåðâîîáðàçíîé äëÿ f (x).
Îïðåäåëåíèå 1. Ôóíêöèÿ F(x) íàçûâàåòñÿ ïåðâîîáðàçíîé äëÿ
ôóíêöèè f (x), åñëè ïðîèçâîäíàÿ F(x) ðàâíà f (x), ò.å.
F ′ (x) = f (x) èëè dF(x) = f (x)dx.
Ïðèìåð. Ïóñòü èìååì ôóíêöèþ f (x) = 2õ. Ôóíêöèÿ F(x) = x
2
ÿâëÿåòñÿ ïåðâîîáðàçíîé äëÿ f (x), ò.ê. (x
2
)′ = 2x. Íî ôóíêöèÿ
F(x) = x
2
+ 1 òîæå ÿâëÿåòñÿ ïåðâîîáðàçíîé ôóíêöèè f (x), òàê êàê
(x
2
+ 1)′ = 2õ, è âîîáùå ëþáàÿ ôóíêöèÿ F(x) = x
2
+ Ñ (ãäå Ñ
ïðîèçâîëüíàÿ ïîñòîÿííàÿ) åñòü ïåðâîîáðàçíàÿ äëÿ f (x). Òàêèì îá-
ðàçîì, äàííàÿ ôóíêöèÿ èìååò ìíîæåñòâî ïåðâîîáðàçíûõ, ïðè÷åì
ìîæíî ïîêàçàòü, ÷òî ëþáûå äâå èç íèõ îòëè÷àþòñÿ äðóã îò äðóãà
íà ïîñòîÿííîå ÷èñëî.
Òåîðåìà 1 (î äâóõ ïåðâîîáðàçíûõ). Åñëè F
1
(x) è F
2
(x) äâå
ïåðâîîáðàçíûå ôóíêöèè f (x) íà îòðåçêå [a, b], òî ðàçíîñòü ìåæäó
íèìè ðàâíà ïîñòîÿííîìó ÷èñëó.
Èç ýòîé òåîðåìû ñëåäóåò, ÷òî åñëè íàéäåíà êàêàÿ-ëèáî ïåðâî-
îáðàçíàÿ F(x) äëÿ ôóíêöèè f (x) íà íåêîòîðîì ïðîìåæóòêå (êîíå÷-
íîì èëè áåñêîíå÷íîì), òî ëþáàÿ äðóãàÿ ïåðâîîáðàçíàÿ ýòîé ôóí-
êöèè ìîæåò áûòü íàéäåíà ïî ôîðìóëå
F(x) = F(x) + C,
ãäå C = const.
147
Îïðåäåëåíèå 2. Ìíîæåñòâî ïåðâîîáðàçíûõ ôóíêöèè f (x) íàçû-
âàåòñÿ íåîïðåäåëåííûì èíòåãðàëîì îò ôóíêöèè f (x) è îáîçíà÷àåò-
ñÿ ñèìâîëîì
I
f (x)dx. Òàêèì îáðàçîì, ïî îïðåäåëåíèþ èìååì:
∫
+= ,)()( CxFdxxf
ãäå F(x) êàêàÿ-ëèáî ïåðâîîáðàçíàÿ; C = const; õ íåçàâèñèìàÿ
ïåðåìåííàÿ èíòåãðèðîâàíèÿ; f (x) ïîäèíòåãðàëüíàÿ ôóíêöèÿ;
f (x)dx ïîäèíòåãðàëüíîå âûðàæåíèå;
I
çíàê èíòåãðàëà.
Îïåðàöèÿ íàõîæäåíèÿ ïåðâîîáðàçíûõ ôóíêöèè íàçûâàåòñÿ åå
èíòåãðèðîâàíèåì.
Ãåîìåòðè÷åñêèé ñìûñë íåîïðåäåëåííîãî èíòåãðàëà. Ãðàôèê
ïåðâîîáðàçíîé F(x) íàçûâàþò èíòåãðàëüíîé êðèâîé. Â ñèñòåìå êî-
îðäèíàò õ0ó ãðàôèêè âñåõ ïåðâîîáðàçíûõ îò äàííîé ôóíêöèè ïðåä-
ñòàâëÿþò ñåìåéñòâî êðèâûõ, çàâèñÿùèõ îò âåëè÷èíû ïîñòîÿííîé
Ñ è ïîëó÷àåìûõ îäíà èç äðóãîé ïóòåì ïàðàëëåëüíîãî ñäâèãà âäîëü
îñè 0ó. Äëÿ ïðèìåðà, ðàññìîòðåííîãî âûøå, èìååì:
∫
+=
.2
2
Cxxdx
Ñåìåéñòâî ïåðâîîáðàçíûõ (õ
2
+ Ñ) ãåîìåòðè÷åñêè èíòåðïðå-
òèðóåòñÿ ñîâîêóïíîñòüþ ïàðàáîë.
Åñëè èç ñåìåéñòâà ïåðâîîáðàçíûõ íóæíî íàéòè îäíó, òî çàäà-
þò äîïîëíèòåëüíûå óñëîâèÿ, ïîçâîëÿþùèå îïðåäåëèòü ïîñòîÿí-
íóþ Ñ. Îáû÷íî ñ ýòîé öåëüþ çàäàþò íà÷àëüíûå óñëîâèÿ: ïðè çíà-
÷åíèè àðãóìåíòà õ = õ
0
ôóíêöèÿ èìååò çíà÷åíèå F(x
0
) = ó
0
.
Ïðèìåð. Òðåáóåòñÿ íàéòè òó èç ïåðâîîáðàçíûõ ôóíêöèè ó = 2 õ,
êîòîðàÿ ïðèíèìàåò çíà÷åíèå 3 ïðè õ
0
= 1.
Ðåøåíèå.
∫
==++=
.2;31;2
22
ÑÑCxxdx
Èñêîìàÿ ïåðâîîáðàçíàÿ: F(x) = x
2
+ 2.
Òåîðåìà 2 (î ñóùåñòâîâàíèè íåîïðåäåëåííîãî èíòåãðàëà).
Åñëè ôóíêöèÿ f (x) íåïðåðûâíà íà îòðåçêå [a, b], òî äëÿ ýòîé
ôóíêöèè ñóùåñòâóåò íåîïðåäåëåííûé èíòåãðàë íà ýòîì æå îò-
ðåçêå.
148
3.1.2. Òàáëèöà îñíîâíûõ èíòåãðàëîâ
Ðàññìîòðèì ñâîéñòâà íåîïðåäåëåííûõ èíòåãðàëîâ.
1.
()
).()( xfdxxf
=
′
∫
2.
(
)
,)()( dxxfdxxfd
=
∫
3.
.)()( CxFxdF +=
∫
4.
∫ ∫
= .)()( dxxfkdxxfk
5.
∫∫∫
+=+
.)()()]()([ dxxdxxfdxxxf
ϕϕ
 èíòåãðàëüíîì èñ÷èñëåíèè íåò îáùåãî ïðèåìà íàõîæäåíèÿ
íåîïðåäåëåííîãî èíòåãðàëà. Ñóùåñòâóåò íåñêîëüêî ìåòîäîâ, êî-
òîðûå äàþò âîçìîæíîñòü ñâåñòè çàäàííûé èíòåãðàë ê òàê íàçûâà-
åìîìó òàáëè÷íîìó. Ïðèåì, êîãäà çàäàííûé èíòåãðàë ìîæíî ñðà-
çó âû÷èñëèòü, èñïîëüçóÿ åãî ñâîéñòâà è òàáëèöó îñíîâíûõ èíòåã-
ðàëîâ, íàçûâàþò íåïîñðåäñòâåííûì èíòåãðèðîâàíèåì.
Òàáëèöû îñíîâíûõ èíòåãðàëîâ ïðèâåäåíû â ñîîòâåòñòâóþùèõ
ðàçäåëàõ ó÷åáíèêîâ, èõ íåîáõîäèìî âûó÷èòü íàèçóñòü.
1.
∫
−≠+
+
=
+
,1,
1
1
nC
n
x
dxx
n
n
ãäå Ñ = const.
2.
∫∫
≠>+=+=
.1,0,
ln
, aaC
a
a
dxaCedxe
x
xxx
3.
.||ln Cx
x
dx
+=
∫
4.
∫
+−= .cossin Cxdxx
5.
∫
+= .sincos Cxdxx
6.
.tg
cos
2
Cx
x
dx
+=
∫
7.
.ctg
sin
2
Cx
x
dx
+−=
∫
8.
.tgarc
1
,tgarc
1
22
2
C
a
x
a
xa
dx
Cx
x
dx
+=
+
+=
+
∫
∫
149
9.
.sarc
,sin
1
22
2
C
a
x
in
xa
dx
Cxarc
x
dx
+=
−
+=
−
∫
∫
10.
.ln
2
1
22
C
ax
ax
a
ax
dx
+
+
−
=
−
∫
11.
.ln
22
22
Caxx
ax
dx
+±+=
±
∫
Íåîáõîäèìî îáðàòèòü âíèìàíèå íà òåñíóþ ñâÿçü ýòîé òàáëè-
öû ñ òàáëèöåé ïðîèçâîäíûõ (çàäà÷à íàõîæäåíèÿ íåîïðåäåëåííî-
ãî èíòåãðàëà ÿâëÿåòñÿ îáðàòíîé ïî îòíîøåíèþ ê çàäà÷å íàõîæäå-
íèÿ ïðîèçâîäíîé). Ïðîöåññ èíòåãðèðîâàíèÿ (íàõîæäåíèÿ íåîïðå-
äåëåííîãî èíòåãðàëà) ïî ñðàâíåíèþ ñ äèôôåðåíöèðîâàíèåì
(íàõîæäåíèåì ïðîèçâîäíîé) ìîæåò ïðåäñòàâëÿòü çíà÷èòåëüíûå
òðóäíîñòè. Ïðè äèôôåðåíöèðîâàíèè çàäà÷à ñâîäèòñÿ ê òîìó, ÷òî-
áû â òàáëèöå ïðîèçâîäíûõ íàéòè ïîäõîäÿùóþ ôîðìóëó, èñõîäÿ
èç êîòîðîé ñ ïîìîùüþ ïðàâèë äèôôåðåíöèðîâàíèÿ âû÷èñëÿåòñÿ
èñêîìàÿ ïðîèçâîäíàÿ çàäàííîé ôóíêöèè. Ïðè èíòåãðèðîâàíèè æå
íåò êàêîãî-ëèáî îáùåãî ïðèåìà âû÷èñëåíèÿ íåîïðåäåëåííûõ èí-
òåãðàëîâ. Èìååòñÿ ëèøü ðÿä ìåòîäîâ, ïîçâîëÿþùèõ ñâåñòè äàí-
íûé èíòåãðàë ê òàáëè÷íûì. Ïîýòîìó äëÿ êàæäîãî äàííîãî èíòåã-
ðàëà íóæíî ñóìåòü íàéòè ïîäõîäÿùèé ìåòîä, ñ ïîìîùüþ êîòîðî-
ãî ïðåîáðàçîâàòü äàííûé èíòåãðàë ê òàáëè÷íîìó âèäó, à çàòåì
íàéòè åãî ïî ñîîòâåòñòâóþùåé ôîðìóëå òàáëèöû èíòåãðàëîâ. Ðàñ-
ñìîòðèì ïðîñòåéøèå ìåòîäû íàõîæäåíèÿ íåîïðåäåëåííûõ èíòåã-
ðàëîâ.
3.1.3. Èíòåãðèðîâàíèå ìåòîäîì çàìåíû ïåðåìåííîé
Ïóñòü òðåáóåòñÿ âû÷èñëèòü èíòåãðàë
∫
,)( dxxf
íå ÿâëÿþùèé-
ñÿ òàáëè÷íûì. Ââåäåì âìåñòî õ íîâóþ ïåðåìåííóþ t, ñâÿçàííóþ ñ
õ çàâèñèìîñòüþ õ =
ϕ
(t), ãäå
ϕ
(t) äèôôåðåíöèðóåìàÿ ôóíêöèÿ,
äëÿ êîòîðîé ñóùåñòâóåò îáðàòíàÿ ôóíêöèÿ. Òîãäà dx =
ϕ
′(t)dt è
áóäåò èìåòü ìåñòî ôîðìóëà:
∫∫
′
=
.)()]([)( dtttdxxf
ϕϕ
(3.1)

150
Âûðàæåíèå (3.1) íàçûâàþò ôîðìóëîé çàìåíû ïåðåìåííîé.
Ñóùåñòâóåò äðóãîé ñïîñîá çàìåíû ïåðåìåííîé èíòåãðèðî-
âàíèÿ.
Åñëè ïîä çíàêîì èíòåãðàëà ñòîèò ñëîæíàÿ ôóíêöèÿ, óìíîæåí-
íàÿ íà ïðîèçâîäíóþ, ò.å.
∫
′
,)()]([ dxxxf
ϕϕ
òî óäîáíî ñäåëàòü çà-
ìåíó u =
ϕ
(õ), du =
ϕ
′(õ)dx, è òîãäà áóäåì èìåòü:
∫∫
=
′
.)()()]([ duufdxxxf
ϕϕ
(3.2)
Îòìåòèì, ÷òî ôîðìóëû (3.1) è (3.2) ðàçëè÷àþòñÿ òîëüêî îáî-
çíà÷åíèÿìè ïåðåìåííûõ èíòåãðèðîâàíèÿ.
Ïðèìåð 3.1. Âû÷èñëèòü èíòåãðàë
.
cos
tg
2
3
dx
x
x
∫
Ñäåëàåì çàìåíó ïåðåìåííîé tg x = t, òîãäà
.
cos
2
)tg(
x
dx
dxxdt
=⋅
′
=
Ïîëó÷èì òàáëè÷íûé èíòåãðàë
,
43
4
1
Ctdtt +⋅=
∫
ãäå Ñ ïðîèç-
âîëüíàÿ ïîñòîÿííàÿ. Ïðîèçâîäÿ îáðàòíóþ çàìåíó ïåðåìåííîé,
ïîëó÷èì:
.tg
4
1
4
1
cos
tg
44
2
3
CxCtdx
x
x
+=+=
∫
Ïðîâåðêà.
x
x
xxCx
2
3
34
cos
tg
4
1
4
1
)tg(tg4tg
==
′
′
⋅⋅+⋅
ïîäèíòåã-
ðàëüíàÿ ôóíêöèÿ.
Ïðèìåð 3.2. Íàéòè èíòåãðàë
∫
+
.
1
dx
x
x
Ââåäåì íîâóþ ïåðåìåííóþ èíòåãðèðîâàíèÿ
.xt =
Òîãäà x = t
2
è dx = 2tdt. Èñïîëüçóÿ ôîðìóëó (3.1), áóäåì èìåòü:
()
.arctg2)arctg(2
1
2
1
1)1(
2
1
22
1
1
22
2
2
2
2
CxxCtt
t
dt
dtdt
t
t
dt
t
t
tdt
t
t
dx
x
x
+−=+−=
=
+
−=
+
−+
=
+
=
+
=
+
∫∫∫∫∫∫
