Shani G. Radiation Dosimetry: Instrumentation and Methods

Подождите немного. Документ загружается.

70 Radiation Dosimetry: Instrumentation and Methods

Equation (2.185) gives in units of MeV/g if



given in g/cm

. To obtain in Gy, one needs to multiply

by the factor , where e is the

elementary charge.

The dose delivered right after the protons have lost

the energy may be written as .

The dose at the actual depth z is then obtained by

folding the Gaussian depth straggling into by means of:

(2.187)

The calculation of , i.e., the consideration of

straggling for the fraction of protons that have nuclear

interactions, is less straightforward but also less critical,

because these protons contribute a smaller and smoother

amount to the total dose.

One can write as the convo-

lution integral [53]

(2.188)

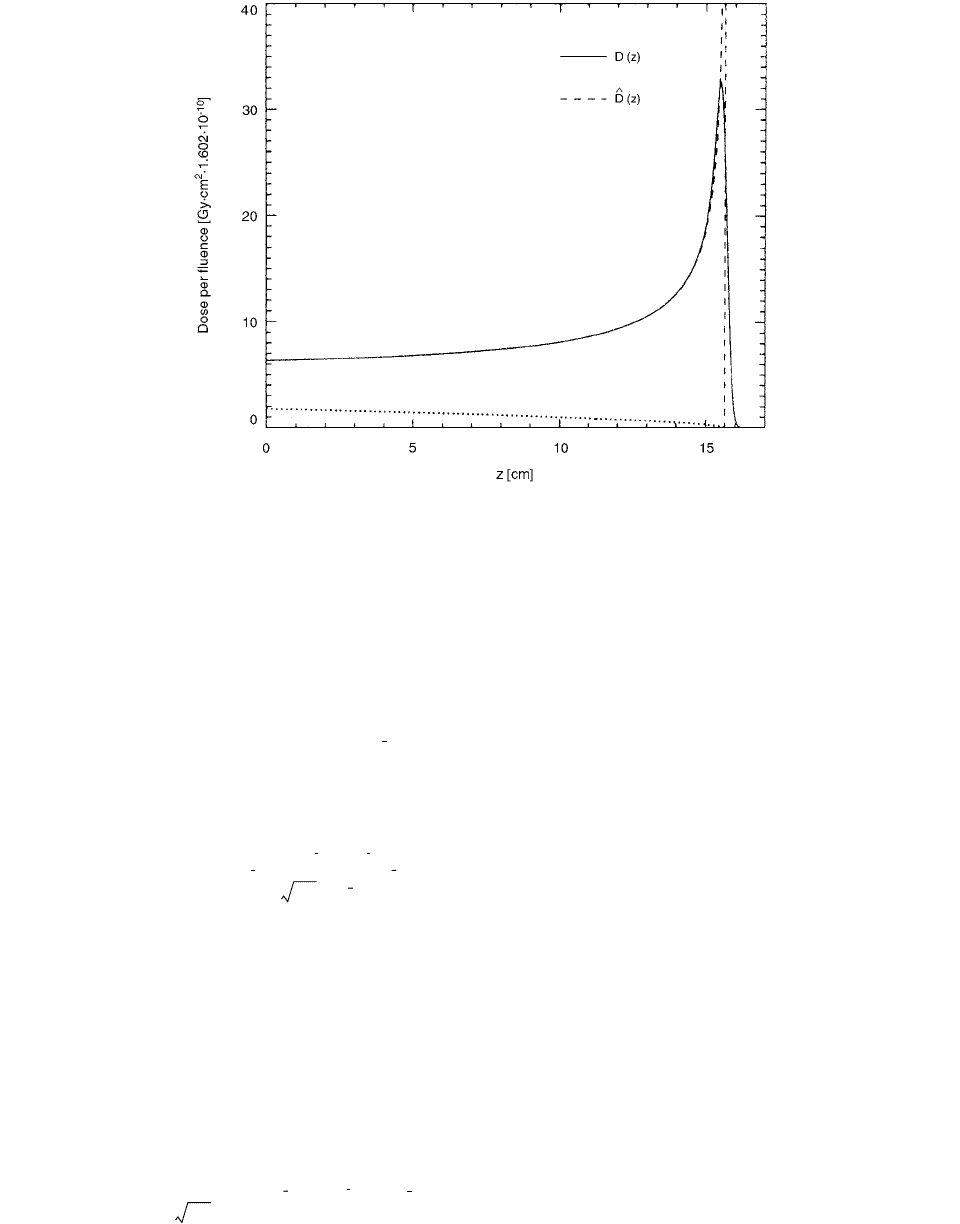
The resulting Bragg curves with and without consid-

eration of straggling are shown in Figure 2.54.

An attempt to include density heterogeneity effects in

the analytical dose calculation models for proton-treatment

planning using a dynamic beam delivery system was made

by Schaffner et al. [54] Different specialized analytical dose

calculations have been developed which attempt to model

the effects of density heterogeneities in the patient’s body

on the dose. Their accuracy has been evaluated by a com-

parison with Monte Carlo calculated dose distributions in

the case of a simple geometrical density interface parallel

to the beam and typical anatomical situations. A specialized

ray-casting model which takes range dilution effects (broad-

ening of the spectrum of proton ranges) into account has

been found to produce results of good accuracy.

The dose calculation of Schaffner et al. consists of a

superposition of individual scanned pencil beams. The

description of the physical pencil beam uses calculated

look-up tables of the depth-dose curve and the depth-width

relation of a proton beam in water. The depth-dose curve

is characterized by the nominal beam energy and the width

of the initial energy spectrum (momentum band). The dose

deposited by a single proton of known initial energy is

derived from the Bethe-Bloch equation.

The formula for the dose deposited at a position (

x, y,

z) by a pencil beam along the z-axis and positioned at

is given by

(2.189)

FIGURE 2.54 Bragg curves with and without consideration of straggling for 150-MeV protons in water. The dotted line at the

bottom is the dose contribution from the fraction of protons that have nuclear interactions, i.e., or (these are

indistinguishable within the resolution of the ﬁgure). (From Reference [53]. With permission.)

z() D

z()

eC 1.602 10

10



E

zEE

,()()

z()

z() D

〈〉z() D

z()

zz()



z()



z()

--------------------------------





z()

Dz() D

z() D

z()

Dz() D

〈〉z()



---------------

z()e

zz()











,()

Dxyz,,()N



ID wer()





-------------------



 x

 x()

2



[]y

 y()

2



[]expexp

Ch-02.fm Page 70 Friday, November 10, 2000 10:53 AM

Theoretical Aspects of Radiation Dosimetry 71

where

ID is the integral dose, interpolated from the depth-

dose look-up table; is the number of protons in

the beam spot; wer is the total water-equivalent range

(range shifter plates plus patient) along the central axis of

the beam; and are the standard deviations of the

Gauasians in

x and y directions. They include all contri-

butions to the beam width, i.e., initial phase space, Coulomb

scattering in the patient and range shifter and its propagation

in the air gap between range shifter and patient.

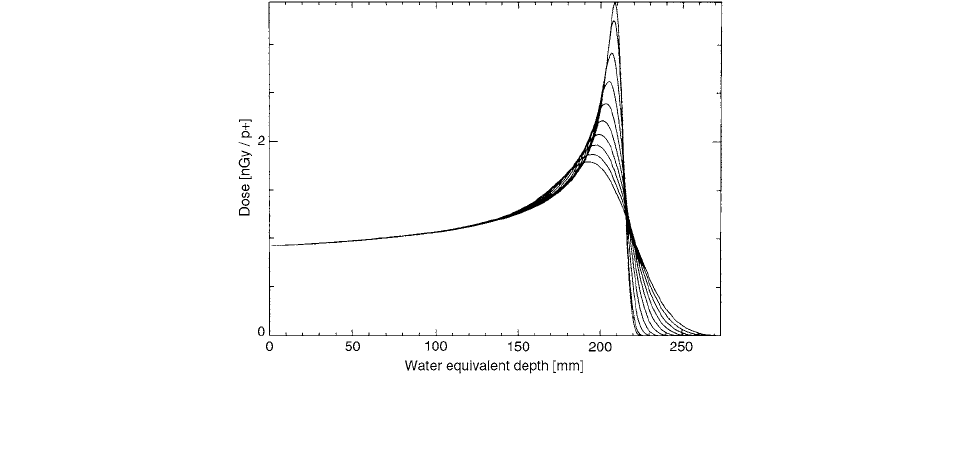
The resulting depth-dose curves for a relative range

dilution from 0 to 9% standard deviation are shown in

Figure 2.55. The inﬂuence of range dilution on the shape

of the Bragg curve is very high in the peak region, while

there are almost no changes in the plateau. This underlines

the importance of the peak region and justiﬁes their

approach of calculating the range dilution only for protons

stopping in the point of interest.

Utilization of air-ﬁlled ionization chambers with

Co-

based reference calibrations in proton dosimetry requires

application of water to air stopping power ratios and the

mean energy required to produce an ion pair (W or w).

Proton dosimetry protocols recommend the use of calorim-

etry as the absorbed dose standard. Siebers et al. [55] used

calorimetry in conjunction with an ionization chamber

with

Co reference calibrations to deduce the proton w

value in the entrance region of a 250-MeV proton beam:

34.2  0.5 eV.

For high-energy charged particles (protons), the dif-

ferential value w is used since only a small fraction of the

particle energy is deposited in the ion chamber gas cavity.

For photon and electron beams, the stopping power ratios

and

W values are known to within a few tenths of 1%.

The dose delivered to the water calorimeter was deter-

mined from [55]:

(2.190)

with being the absorbed dose to water, c the spe-

ciﬁc heat of water, T the change in water temperature

measured using the thermistors, and the thermal defect

of water. Water temperature changes were monitored using

a Wheatstone bridge circuit. is expressed in terms of

the Wheatstone bridge deﬂection and the thermistor

calibration factor  as

(2.191)

To evaluate ionization dosimetry, measurements were

made in a geometry similar to that used for the calorimeter

measurements through use of the dummy calorimeter. In

place of the thermistors, a Farmer-type PTW ionization

chamber (model W30001, volume 0.6 cm

, PMMA walls,

aluminum central electrode) was inserted into a water-

proof PMMA cap which was securely mounted in the core

region. Ionization charge measurements were made for

runs of length equal to that of the water calorimeter runs.

The ionization chamber calibration factor in the pro-

ton beam was determined from the calorimeter and ion

chamber responses by applying the recommendations of

the AAPM and ECHED code of practice.

(2.192)

FIGURE 2.55 Depth-dose curve for a 177-MeV beam with a momentum band of 1.1% and with a relative range dilution of 0–9%

in steps of 1%. (From Reference [54]. With permission.)

wer wer x

z,,()



wer x

z,,()()with ixy.,





c water,

cT 1 D

()

c water,

T

V

T V



c water,

ion

CIS, att()

----------------------------------------



Ch-02.fm Page 71 Friday, November 10, 2000 10:53 AM

72 Radiation Dosimetry: Instrumentation and Methods

where is the proton calibration factor, is the

dose measured using the calorimeter [Equation (2.190)],

and M is the charge collected in the ionization chamber,

corrected to reference temperature and pressure condi-

tions. corrects for recombination in the ionization

chamber and corrects for inverse square and

attenuation (depth-dose) variations due to minor geomet-

ric differences between the calorimeter and the dummy

calorimeter. The proton calibration factor for an ionization

chamber with a

Co reference calibration is

(2.193)

To determine , the calorimeter-based calibration

factor [Equation (2.192)] is set equal to the calibration

factor determined from the

Co-based calibration.

is solved to reveal

(2.194)

In Equation (2.194), the subscript air refers to dry air,

whereas gas denotes humid air. The equivalence

can be made by assuming that

humidity corrections to w values are independent of irra-

diation modality.

X. CAVITY THEORY

Cavity theory is used to relate the radiation dose deposited

in the cavity (the sensitive volume of the detector) to that

in the surrounding medium. The dose to the cavity

depends on the size, atomic composition, and density of

the cavity and the surrounding medium. The size of the

cavity is deﬁned relative to the range of the electrons set

in motion. A cavity is considered small when the range

of the electrons entering the cavity is much greater than

the cavity dimensions. The electron spectrum within a

small cavity is solely determined by the medium surround-

ing the cavity. The ratio of absorbed dose in the cavity to

that in the surrounding medium is given by the Bragg-

Gray or Spencer-Attix theory. When the cavity dimensions

are many times larger than the range of the most energetic

electrons, the electron spectrum within the cavity is deter-

mined by the cavity material. A cavity whose dimensions

are comparable to the range of electrons entering the cav-

ity has a spectrum within the cavity that is partially deter-

mined by the medium and partially determined by the

cavity material. Burlin proposed a general cavity theory

to include all cavity sizes

A detector will give a signal proportional to the absorbed

dose in the sensitive detector material, which in general

differs from the medium. One can write

(2.195)

where is the dose to the radiation-sensitive material,

is the dose to the medium, and

f is the ratio of the

two doses. In case of photon radiation, the factor f can be

given either by the mass stopping power ratio , if

the detector is small compared to the electron range

(Bragg-Gray cavity), or by the ratio of the mass energy

absorption coefﬁcients , if the detector is

large compared to the electron range. For both categories

Burlin’s theory yielded expressions combining both

and .

According to Bragg-Gray theory, Equation 2.195

becomes

where

is the mass stopping power ratio, is the charge

collected per unit mass of air, and

W/e is the energy

required to create one ion pair in air. When the incident

photon energy decreases, the energy absorbed in air in the

chamber increases and will ﬁnally invalidate the Bragg-

Gray condition.

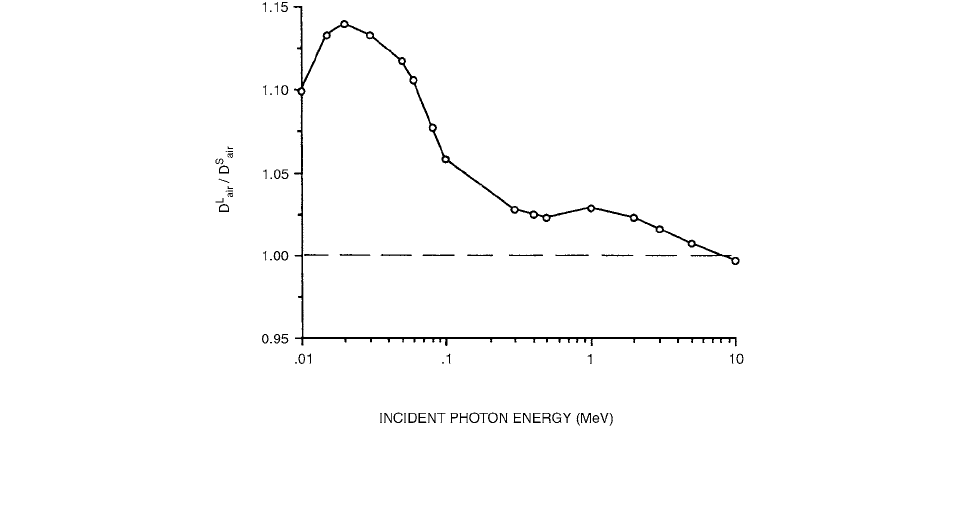
The validity of the Bragg-Gray cavity theory in photon

radiation dosimetry for photon energies from 10 keV to

10 MeV has been investigated by Ma and Nahum [56]

quantitatively. The ratio of the absorbed dose result-

ing from photon interactions in an air cavity to that

in air under the condition of charged-particle equilibrium

has been used as a parameter to determine if the air

cavity can be classiﬁed as a Bragg-Gray cavity. Burlin

general cavity theory seriously overestimates the depar-

ture from Bragg-Gray behavior. For clinical photon

beams, the dose ratio is 0.29 for a 150-kVp beam and

0.27 for a 240-kVp beam, compared to 0.006 for a

Co-

beam, if the cavity is placed at a depth of 5 cm in water.

The study conﬁrms that typical air-ﬁlled ionization cham-

bers cannot be considered to be Bragg-Gray cavities for

low- and medium-energy photon radiation.

For a given absorbed dose to the medium, , the

absorbed dose to the sensitive detector material in the case

of a small detector, , is in general different from that

for a large detector, . By substituting and

into Equation (2.195), in turn, one obtains

(2.196)

Figure 2.56 shows how the dose ratio, , cal-

culated using Equation (2.196), varies with energy when

a monoenergetic photon beam is incident on water and

c water,

ion

CIS, att()

gas

W



()

gas



,()

gas

water



W



()

gas

W



()

gas

W



()

air



c water,

gas



,()

gas

water

ion

C IS att,()

---------------------------------------------------------------------------------



W



()

gas

W



()

air



med

det



det

med

med,det







()

med,det







()

med,det

med

air

med,air



air

We()

med,air

air

med

det

med,det







()

med,det

det

D

det

med,det







()

det,med



det

D

det

Ch-02.fm Page 72 Friday, November 10, 2000 10:53 AM

Theoretical Aspects of Radiation Dosimetry 73

the (air-ﬁlled) detector is placed at a depth of 8 cm in

water (chosen to be greater than the maximum possible

CSDA electron range at all energies). The value of is

usually smaller than that of and the difference between

increases as the incident photon energy

decreases. This means that signiﬁcant dosimetric errors

could be introduced by using such detectors at lower pho-

ton energies.

Suppose that an air cavity (i.e., without walls) is

placed at a depth in water where charged-particle equilib-

rium (CPE) has been established. The mean absorbed dose

in the air cavity, , can be divided into two parts; i.e.,

(2.197)

where is the dose resulting from the electrons gener-

ated by photon interactions in the surrounding water and

is the dose resulting from photon interactions in the

air cavity. If and the disturbance by the detec-

tor of the electron ﬂuence present in the undisturbed water

is negligible, then the absorbed dose in the air cavity

depends solely upon the electron ﬂuence present at the

depth of interest in water (the condition for Bragg-Gray

theory to apply). If is close to , the absorbed dose

in air under the CPE condition, then the absorbed dose in

the air cavity depends mainly upon the photon ﬂuence

present at the depth of interest in water (the condition for

large detectors). For the intermediate case, if one still uses

the Bragg-Gray cavity theory, errors will occur, the severity

of which can be judged from Figure 2.56.

Let the quantity be a measure of

the validity of the Bragg-Gray cavity theory at different

photon beam energies; the condition for the Bragg-Gray

cavity theory to apply is . For a monoenergetic

photon beam of energy E, we have

(2.198)

where

 is the photon ﬂuence and is the mass

energy absorption coefﬁcient of air at energy E. The dose

ratio, , for a monoenergetic photon beam of energy E

can then be expressed as

(2.199)

Suppose that one has a photon spectrum and wishes

to calculate the corresponding quantity, , for the

spectrum. This can be done by integrating over

the photon spectrum according to [56]

where is the photon ﬂuence, differential in energy,

and ( is the mass energy absorption coefﬁ-

cient for air at energy

The Burlin general cavity relation can be written as

(2.200)

FIGURE 2.56 The variation with the incident photon energy of the dose ratio, at a depth of 8 cm in water calculated

using Equation 2.196. The mass energy absorption coefﬁcient ratios and the mass stopping power ratios were calculated using Monte

Carlo techniques. (From Reference [56]. With permission.)

air

D

air



air

 D

air

CPE

air

D

air



air

0→

air

CPE

E







()

air









()

air

E() D

air



 E







()

air

spec

air

E()

air

spec

air

E()



E()



()

air

Ed

max









(

E()



)

air

max







E()



)

air

det

det med,

1 d()







()

det med,

[]D

med



Ch-02.fm Page 73 Friday, November 10, 2000 10:53 AM

74 Radiation Dosimetry: Instrumentation and Methods

where d is a parameter related to the cavity size that

approaches unity for small cavities and zero for large ones.

Burlin expresses (1  d) as

(2.201)

where L is equal to four times the cavity volume, V, divided

by its surface area, with



satisfying

(2.202)

That is, the maximum depth of electron penetration, T, is

to be arbitrarily taken as the depth to which only 1% of

the electrons can travel.

Suppose the CPE condition has been established and

the values of and are known. Then

one can write

(2.203)

By combining Equation (2.203) with equation (2.197),

one obtains [56]

(2.204)

By comparing Equations (2.200) and (2.204) and not-

ing that , Ma and Nahum arrived at

(2.205)

(2.206)

It is worth noting that, since is in general differ-

ent from either or , it is evident that [56]

(2.207)

This is ignored in the Burlin theory.

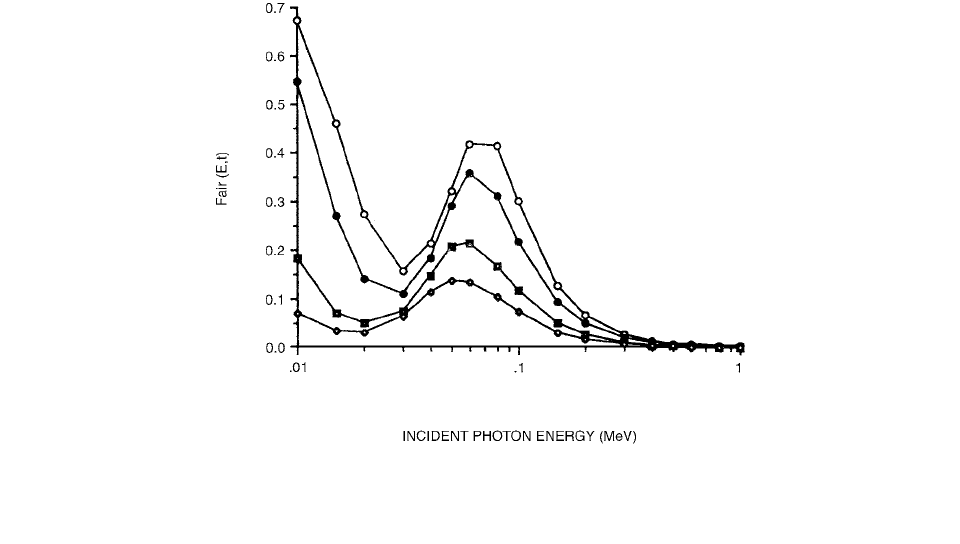
Figure 2.57 shows the ratio of the absorbed

dose in an air cavity of thickness

t and 6-mm diameter in

vacuum to that in air under the condition of CPE for

monoenergetic photon beams. Above about 0.1 MeV, the

dose ratio decreases rapidly with the incident

photon energy and becomes negligible for high photon

energies (smaller than 0.01 for photon energies above

500 keV). The curves exhibit maxima between

50 and 80 keV [ (80 keV, 6 mm)  0.41, (60 keV,

3 mm)  0.37, (60 keV, 1 mm)  0.22, and 

(50 keV, 0.5 mm) 0.14]. The fraction of the photon

energy transferred to Compton electrons decreases

steadily with decreasing photon energy, whereas, for pho-

toelectrons, this fraction is essentially unity. As a conse-

quence of more secondary electrons resulting from

Compton interactions than from photoelectric interac-

tions, the total average energy transfer actually decreases

for photon energies greater than 20 keV, increasing again

only for photon energies greater than 60 keV.

Comparing values with the (1  d) values in Burlin

theory, we note the following. In Figure 2.58, the values of

(l  d) normalized to are presented as a function

of photon energy for monoenergetic photon beams. The

Monte Carlo calculated results of the dose ratio, ,

show a much smaller fraction of the absorbed dose in the

FIGURE 2.57 The variation with the incident photon energy, E, of for an air cavity of thickness t and 6-mm diameter

in vacuum irradiated by monoenergetic photon beams. The Monte Carlo calculational uncertainty is smaller than 0.5%.

, t 

0.5 mm; , t 1 mm; , t  3 mm; , t  6 mm. (From Reference [56]. With permission.)

air

Et,()

1 d()



L

1()



L

0.01

det med,







()

det med,

med

med det,

det







()

med det,

det



air

D

med

air

D

air

()S

air med,



air

D

air

()







()

air med,



air



air

D

air

CPE

1 d

air

D

air

d

air

D

air

()D

air

D

air

()1

air

Et,()

air

Et,()

air

Et,()

air

E()

air

)

Ch-02.fm Page 74 Friday, November 10, 2000 10:53 AM

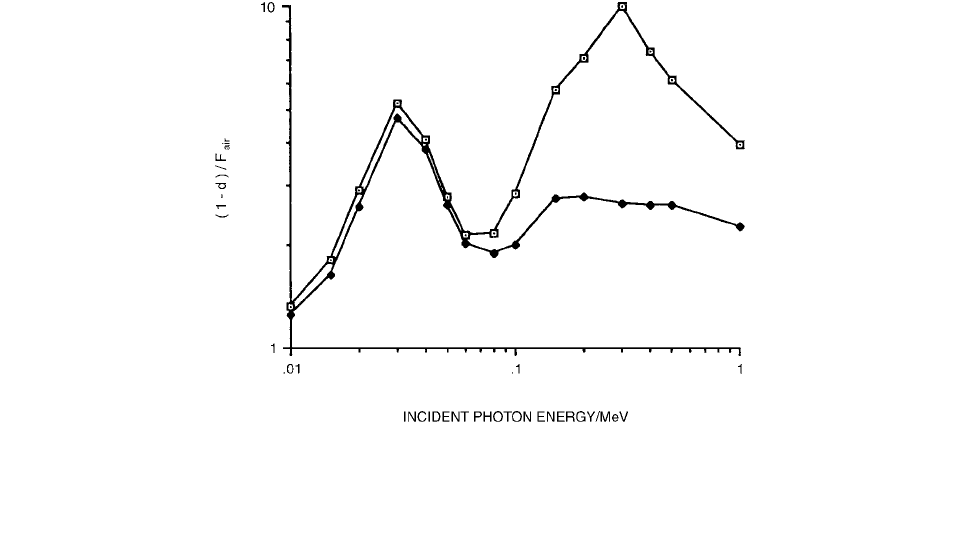
Theoretical Aspects of Radiation Dosimetry 75

air cavity resulting from the direct photon interactions

with the air in the cavity compared to that predicted by

Burlin theory. Using 0.04 instead of 0.01 in Equation

(2.202) only slightly reduces the difference between

and (l  d).

The Burlin theory ignores all secondary-electron scat-

tering effects which results in large discrepancies in dose

to the cavity compared with the experimental results in

high atomic number media. Kearsley [57] proposed a new

general cavity theory which includes secondary-electron

scattering at the cavity boundary. The Kearsley theory

showed excellent agreement with experimental results for



-rays but poor correlation for 10-MV x-rays. The

Kearsley theory has numerous parameters and the magni-

tude of the input parameters is arbitrary; therefore, the

dose to the cavity depends on the choice of parameters.

Haider et al. [58] have developed a new cavity theory which

includes secondary-electron backscattering from the

medium into the cavity. The strength of this proposed theory

is that it contains few parameters and a methodical way of

determining the magnitude of the parameters experimen-

tally. The theory gives better agreement with experimental

results in lithium ﬂuoride thermoluminescence dosimeters

for



-rays and 10-MV x-rays in aluminum, copper,

and lead than do the Burlin and Kearsley cavity theories.

Haider et al. assume that the Compton interaction is

the dominant radiation interaction and, thus, the applicable

energy range of the theory is from 500-kV to 20-MV x-

rays. The electron density is proportional to the energy

loss cross section of electron stopping power which is

mainly determined by the excitation energy of the mole-

cules and the Compton scatter cross section. When the

Compton process is dominant and the difference of mean

excitation energies per electron is small, then the stopping

power ratio averaged over the cavity volume is equal to

the ratio of electron densities, independent of cavity size.

The total electron ﬂuence in the cavity of

thickness

t is divided into three groups: [58]

1. the electron ﬂuence that originated in the cavity,

including the backscattered electrons generated

by it in the cavity traveling in the opposite direc-

tion ;

2. the electron ﬂuence that originated in the

front-wall medium, including the backscat-

tered electrons generated by it in the cavity

traveling in the opposite direction ;

and

3. the electron ﬂuence in the cavity resulting from

the difference in the backscattering coefﬁcients

of the cavity medium and the back-wall medi-

um .

In the following, w is referred to as the front-wall medi-

um, g as the cavity medium, m as the back-wall medium,

and b as the backscattering coefﬁcient. The electron ﬂu-

ence in the cavity is given by

(2.208)

FIGURE 2.58 Values of the ratio (1  d)/ for an air cavity of 6-mm thickness and 6-mm diameter in vacuum; (l  d) was

calculated using Equation (2.201) with

L  4 mm. For Burlin’s (l  d),



was calculated using Equation (2.202) with T  0.95

. For Janssens et al.’s [73] (1

 d), a constant of 0.04 was used in place of 0.01 in Equation (2.202). , Burlin; , Janssens

et al. (From Reference [56]. With permission.)

air

E()

SCDA

air

E()



egT,,

z()()



eg,

z()()



ew,

z()(

)



emb,,

z()()



egT,,

z() 

eg,

z() 

ew,

z() 

emb,,

z()

Ch-02.fm Page 75 Friday, November 10, 2000 10:53 AM

76 Radiation Dosimetry: Instrumentation and Methods

Therefore, the dose to the cavity is given by

(2.209)

where is the mean mass collision stopping power. In

the absence of the cavity, the dose to the wall is given by

(2.210)

where the subscript c denotes the equilibrium ﬂuence in

the wall medium (i.e., under charged particle equilibrium

(CPE), where dose is equal to the collision part of the

kinetic energy released in medium A (kerma). The ratio f

of the average dose to the cavity (g) and to the front wall

medium (w) is given by

(2.211)

where is the ratio of the mean mass collision

stopping powers of medium

g and of medium w. ,

, and are functions of the distance z from the

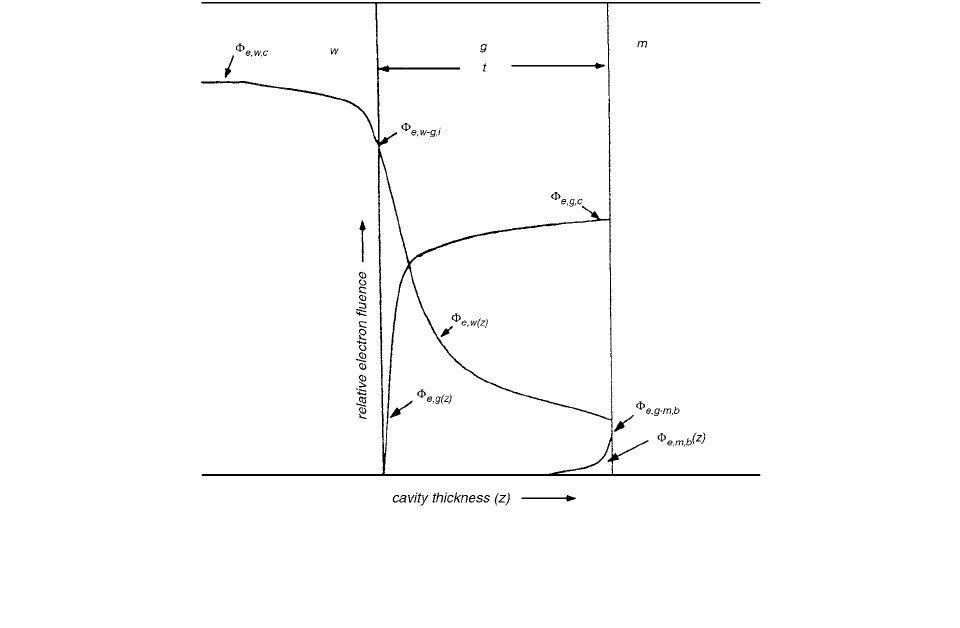
front cavity interface (Figure 2.59). Each term can be

represented by the product of a distance-independent elec-

tron ﬂuence term at the interface and a distance-dependent

weighting factor. Therefore, [58]

(2.212)

where is the equilibrium cavity ﬂuence, is

the electron ﬂuence at the front wall-cavity (w-g) inter-

face, is the electron ﬂuence at the back wall-

cavity (g  m) interface, and , and are dependent

weighting factors: is the ratio of the electron ﬂuence

generated in the cavity medium at a distance z from the

front wall-cavity interface and the equilibrium ﬂuence in

the cavity medium; is the ratio of the electron ﬂuence

generated in the front wall medium at a distance z from

the wall-cavity interface (Figure 2.59) and the electron

ﬂuence at the front wall-cavity interface; and is

the ratio of the backscattered electron ﬂuence at a distance

(t  z) from the back wall-cavity interface to the back-

scattered electron ﬂuence at the cavity-back wall interface.

If the cavity and the wall materials are irradiated by

the same photon ﬂuence separately, then the dose ratio

between the cavity and the wall under CPE is related by

the ratio of the average mass energy absorption coefﬁ-

cients. Therefore,

(2.213)

FIGURE 2.59 Illustration of cavity parameter. is the electron ﬂuence that originated in the cavity (g), including its

backscatter. is the electron ﬂuence spectrum that originated in the front-wall medium (

w) and its backscatter as it crosses

the cavity. is the electron ﬂuence spectrum in the cavity resulting from the difference in the backscattering coefﬁcient of

the cavity (

g) and the back-wall medium (m). (From Reference [58]. With permission.)



eg,

z()



ew,

z()



emb,,

z()



egT,,

z()S



〈〉





eg,

z() 

ew,

z() 

emT,,

z()()S



〈〉



S



〈〉



ewc,,

z()S



〈〉



fz()



eg,

z() 

ew,

z() 

emb,,

z()



ewc,,

--------------------------------------------------------------------------

S



〈〉



S



〈〉



ew,



emb,,

fz() 

z()

ewc,,

z()

ewgi,,

z()

egmb,,





ewg,

----------------------------------------------------------------------------------------------------------------

S



〈〉





egc,,



ew-gi,,



e, gm, b

, C

-------







〈〉



Ch-02.fm Page 76 Friday, November 10, 2000 10:53 AM

Theoretical Aspects of Radiation Dosimetry 77

where is the mean mass energy absorption coef-

ﬁcient. The dose ratio between the cavity and the wall is

also related by

(2.214)

using the relationship of Equation 2.210:

(2.215)

Let

F be the fraction of the total number of electrons

per unit area which crosses a reference plane r from left

to right in a medium under CPE and let b be the fractional

number of incident electrons that are backscattered from

the reference plane r traveling from right to left. In a

homogeneous medium, the total number of electrons or

the equilibrium ﬂuence which includes the backscat-

tered electrons traveling in the opposite direction is given

(2.216)

The term is the total number of electrons per unit

area which crosses a reference plane r from left to right

and the team is the total number of backscattered

electrons crossing the same reference plane from right to

left. If the medium to the left of the reference plane r is

w and to the right of the reference plane is g, then the

electron ﬂuence at the interface of w  g is

given by [58]

(2.217)

where is the fractional forward electron ﬂuence orig-

inating in the medium w and b

is the probability of back-

scattering of the medium g. If medium g of thickness t is

sandwiched between medium w and medium m, then the

relative backscattered electron ﬂuence between medium g

and medium m at the interface g  m ( ) is given by

(2.218)

where is the fractional forward electron ﬂuence

of the total electron ﬂuence arriving at the inter-

face

g  m; is the backscattering coefﬁcient of the

medium m; and is the difference in the backscat-

tering coefﬁcient of medium g and medium m. Electron

backscattering within the medium g is already accounted

for in , and . consists of and ,

evaluated at cavity thickness t given by

(2.219)

where is the fractional forward electron ﬂuence orig-

inating in the cavity medium and is the fractional

forward electron ﬂuence originating in the front-wall

medium. and can be expressed by a prod-

uct of cavity size–independent electron ﬂuence terms and

cavity size–dependent weighting factors. Therefore,

(2.220)

where and are the fractions of the electron ﬂuences

and , respectively, that arrive at the interlace

g  m of cavity thickness t.

When the cavity size is very large compared with the

range of the electrons, the above equations lead to the ratio

of the mass-energy absorption coefﬁcients of cavity and

medium as in the Burlin and the Kearsley cavity theories.

When the cavity size is very small compared with the

range of the electrons and the front-wall and back-wall

mediums are identical, f reduces to the Bragg-Gray theory.

However, when the front and the back walls are not iden-

tical, f does not reduce to the Bragg-Gray theory. Since

the contributions from the front-wall, cavity, and back-

wall mediums are calculated separately, all three media

could be of different atomic composition. [58]

The weighting factors and are given by

(2.221)

where is the effective electron absorption coefﬁcient

(cm

1

) in the cavity. [58]

XI. ELEMENTS OF MICRODOSIMETRY

Radiation dose in conventional dosimetry is a macroscopic

concept. Target volumes are many orders of magnitude

greater than the individual cellular entities which make up

tissue. The dose to a macroscopic multicellular volume is

obtained by the summation of the total energy deposited

by multiple radiation tracks over the volume divided by

the mass of that volume. Microdosimetry is the study of

radiation energy deposition within microscopic volumes,

where “microscopic” encompasses sensitive target volumes

ranging from the diameter of a cell (typically 20 mm) down

to the diameter of the DNA molecule (2



m). Although

microdosimetry is concerned with the same concept of

energy deposition per unit mass as dosimetry, the differ-

ence in size of the target volume of interest introduces

stochastic effects which are negligible in conventional

dosimetry. The magnitude and importance of stochastic

ﬂuctuations in the target volumes depend greatly on the

target diameter, on the energy and linear energy transfer

(LET) of the particles, and on the relative number of

particles, i.e., the magnitude of the radition dose.

The ﬂuctuations of energy deposition are incorporated

in the stochastic quantities of a subdiscipline of radiolog-

ical physics that has been termed microdosimetry. By

focusing on actual distributions of absorbed energy rather







〈〉

-------







〈〉





ewc,,



ewc,,







〈〉

S



〈〉





ec,



ec,

F

ec,

1 b()

F

ec,

Fb

ec,



e, wg,i

()



e, wg,i



ewc,,

1 b

()



e, wg,i



e, gm,b

e, gm,i



e, gm,i

()

e, gm, i



e, gm, i





eg,



ew,



e, gm, i



eg,



ew,

e, gm, i



e, gm, i



eg,

t() F



ew,

t()



eg,

t() 

ew,

t()

e, gm, i



e, gm, i



egc,,



e, wg, I





egc,,



e, wg, I

1 d

()1



t()exp



Ch-02.fm Page 77 Friday, November 10, 2000 10:53 AM

78 Radiation Dosimetry: Instrumentation and Methods

than on their expected (mean) values, microdosimetry has

demonstrated the complexity of the problem of ﬁnding a

numerical index of radiation quality. On the other hand,

a realistic view of the pattern of energy absorption in

irradiated matter is essential for an understanding of the

mechanisms responsible for radiation effects, not only in

radiobiology but also in such ﬁelds as radiation chemistry

and solid-state dosimetry, and microdosimetry is required

in theoretical approaches to these subjects. Considerable

effort has therefore been expended in the measurement

and calculation of microdosimetric spectra. Once appro-

priate microdosimetric data were obtained, there were

efforts to employ them in radiobiology, radiation chemis-

try, and solid-state research. Such activities ran parallel

with further efforts in instrument design and an important

fundamental analysis of microdosimetry. [59]

The microdosimetric quantity that was ﬁrst formulated

bears a relation to LET and it was, in fact, determined in

g scheme to derive t(L) by measurements of energy dep-

osition in a microscopic region termed the site. In a

spherical proportional counter made of tissue-equivalent

(TE) plastic, the energy that is deposited by an event (i.e.,

the passage of a charged particle) in a TE gas volume of

density



and diameter d is a good approximation to the

energy that would be deposited in unit density tissue

within a site of diameter d



. Since in the proportional

counters utilized,



is typically of the order of 10

5

, it is

possible to simulate very small tissue regions with

counters of convenient size. The quantity measured by

these devices was originally termed the “event size.” In a

later change, this became the lineal energy

y, which has

also been given a slightly different deﬁnition: [59]

(2.222)

where



is the energy deposited in an event and l is the

mean chord length in the tissue region simulated. (Origi-

nally the “event size’’ Y was deﬁned as



/d, with d being

the diameter of the sphere. The newer deﬁnition of y

permits generalization to other shapes. In the case of the

sphere, l  2d/3.) This can be changed readily from a few

tenths to at least several tens of micrometers by a change

of gas pressure. Utilizing modern low-noise preampliﬁers,

it is possible to measure most of the pulses corresponding

to a single ionization. (Because of the statistics of ava-

lanche formation in the proportional counter, initial ion-

izations result in a range of pulse heights). Pulse-height

analysis permits determination of the probability (density)

distribution f(y), i.e., the probability that the lineal energy

of an event is equal to y. A typical, widely used, TE-

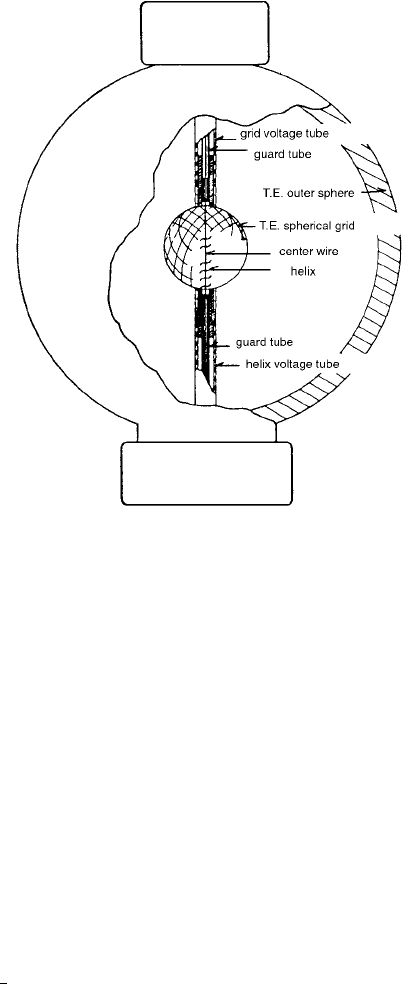
counters design is illustrated in Figure 2.60. An example

for

Co y radiation is given in Figure 2.61.

The quantity termed the speciﬁc energy z (the original

name and symbol were “local energy density, Z”), which

applies to any number of events, is the stochastic analogue

of the absorbed dose and deﬁned by

(2.223)

where



is the energy absorbed in a mass m in the receptor.

D, the average value of the absorbed dose in m, is equal

to , the average value of z.

The speciﬁc energy z that is produced by an event can

be expressed in terms of y because the mean chord length

in a convex body is 4V/S where V is the volume and S is

the surface. Accordingly,

(2.224)

where



is the density. For a unit density sphere,

(2.225)

when

z is expressed in gray, y in keV/



m, and d in



Because of the statistical independence of events, a



l

FIGURE 2.60 Typical spherical proportional counter for micro-

dosimetry. The electrically grounded shell is molded from tissue-

equivalent (TE) plastic and the insulators are made of Lucite.

The spherical grid (TE) serves to largely eliminate the wall effect

that causes separate events in the simulated tissue regions to

coincide in the counter. The helix reduces variations of the electric

ﬁeld along the center wire. These electrodes are of stainless steel.

The counter is traversed by TE gas at a pressure of the order of

Pa. The potential of the center wire is several hundred volts

positive and the potential of the helix is about 20% of this. The

spherical grid is at negative potential. An internal



or soft

x-ray source serves to calibrate the counter. (From Reference

[59]. With permission.)



m

z 4y S



()

z 0.204 yd



Ch-02.fm Page 78 Friday, November 10, 2000 10:53 AM

Theoretical Aspects of Radiation Dosimetry 79

knowledge of f(y) permits calculations of f(z,D), the prob-

ability (density) distribution for any value of the absorbed

dose D. This calculation involves , the frequency-averaged

speciﬁc energy in single events:

(2.226)

From this, one can obtain the mean number of events

n at dose D:

(2.227)

At sufﬁciently small values of D, there is usually no

event in a site and very rarely more than one. f(z, D) then

consists of a Dirac delta function



(z) and the single-event

distribution . This distribution has the same shape

f(y) and any reduction in D merely increases the relative

contribution of the delta function and reduces the fraction

of sites that receive an invariant spectrum of ener-

gies deposited in single events. At large values of D, when

, multiple events ultimately cause f(z, D) to assume

a bell-shaped curve about D. [59]

The product between the point-pair distance distribu-

tion and the measure of the site is termed the proximity

function of that domain. Thus, one has a proximity func-

tion of energy deposition

(2.228)

and a proximity function of the sensitive matrix

(2.229)

t(r)dr can also be deﬁned as the expected energy imparted

to a shell of radius r and thickness dr centered at a ran-

domly chosen transfer point.

Proximity functions t(x) can be calculated from Monte

Carlo generated particle tracks. For monoenergetic parti-

cles (energy

T) one has

(2.230)

where

i and k refer to energy transfers, and , separated

by a distance between r and r  r. The expectation value

refers to an ensemble of tracks. In simple cases t(r) can

be calculated directly. For a track segment with constant

LET, L (no radial extension of the track)

(2.231)

For a homogeneous distribution of energy transfers in

a medium of density exposed to dose D:

(2.232)

Equations (2.231) and (2.232) follow directly from the

deﬁnition of t(r). t(r) can not increase faster than for

any three-dimensional structure. The proximity function

can also be obtained directly from a series of microdosi-

metric measurements of in spherical sites of diam-

eter d: [59]

(2.233)

Microdosimetric concepts in radioimmunotherapy

were discussed by Humm et al. [60] There are three

principal areas where microdosimetry has been applied:

radiation protection; high LET radiotherapy, e.g., neu-

tron therapy; and incorporated radionuclides. In this lat-

ter category the importance of microdosimetry to the

radiobiology of radiolabeled antibodies is becoming

increasingly recognized. The objective of microdosime-

try is the complete characterization of energy deposition

FIGURE 2.61 Microdosimetric spectra for

Co gamma radia-

tion. The spectra represent, from top to bottom, the following

site diameters: 8, 4, 2, 1, and 0.5 nm.

yf(y) is the relative fraction

of the absorbed dose in

y. In this plot, multiplication of the

ordinate by another factor

y makes the area under the curve

proportional to the logarithmic interval in the abscissa. (From

Reference [59]. With permission.)

z()zf

z() zd









1







nDz



z()

n 1

tr() total energy()p

track

r()

sr() site volume()P

site

r()

tr()rE

---

ik,









tr()dr 2L dr

tr() 4





D

r()

tr()

3dr

-----------

----

-----

r()





r()



Ch-02.fm Page 79 Friday, November 10, 2000 10:53 AM