Shani G. Radiation Dosimetry: Instrumentation and Methods
Подождите немного. Документ загружается.


100 Radiation Dosimetry: Instrumentation and Methods
where W
pr,air
and W
,air
are the mean energies needed to
produce one ion pair in air for protons and
60
Co gamma
rays; is the stopping power ratio of water to
air for a proton beam with quality Q
1
at the measurement
point; is the stopping power ratio of water to
air for the reference
60
Co beam; and and
are the perturbation factors. Using the formalism pre-
sented by Loevinger, the perturbation factor for
the reference
60
Co beam was calculated using data from
the TG 21 protocol:
(3.33)
where
P
repl
is the replacement correction factor and P
wall
is the wall correction factor.
When beams Q
0
and Q
1
are proton beams, the ratio
of absorbed doses to water (the proton beam quality cor-
rection factor
k
Q
p
) is simply the ratio of the stopping power
ratios at the two energies:
(3.34)
The proton
W-values for air and perturbation factors cancel
since they are energy independent. As in Equation (3.32),
the effective energy of protons at calibration depth was
used to select the stopping power ratios. [15]
Measured k
Q
values for the Capintec PR-06 and the
PTW W30001 ion chambers are shown in Table 3.6. A
comparison of the results obtained with the different cal-
ibration methods is presented in Table 3.7.
C. CYLINDRICAL IONIZATION CHAMBERS
Correction factors were derived by Seuntjens [18] for a
cylindrical NE2571 ionization chamber, for absorbed dose
determinations in medium-energy x-rays. These new cor-
rection factors are proposed as weighted mean values of
the factors derived from two methods.
Let M
u
denote the electrometer reading for measure-
ments in the phantom. N
K
is the air-kerma calibration
factor and is the ratio of the mean mass energy
absorption coefficients, water to air, both averaged over
the spectral energy fluence distribution of the photons at
the point of measurement in the water phantom for the
radiation quality of interest.
In ionometry the absorbed dose can be derived from
(3.35)
The total correction k k
k
st
p
disp
(to be compared
with k
u
p
u
in the IAEA code) comprises three components:
k
, a correction factor for the energy and angular depen-
dence of the response of the ionization chamber within
the water phantom; k
st
, a correction factor for the influence
of the stem on the photon radiation field, both free in air
and in phantom; and p
disp
, a correction factor taking into
account the perturbation of the photon radiation field by
the chamber volume displacing the phantom material,
which is defined as the volume limited by the outer dimen-
sions of the chambers, i.e., the sensitive air cavity and the
chamber wall but without the stem.
The correction factor
k
is derived as follows. The
response of the ionization chamber at the reference point
in water is defined as the ratio R
w
M
u
/K
air,w
, where M
u
is the meter reading in water and K
air,w
is the air kerma at
TABLE 3.6
A Comparison of Measured and Calculated Proton K
Q,r
Values
250 MeV 155 MeV
Calculated Measured Calculated Measured
PTW W30001 1.020 0.045 1.032 0.012 1.022 0.046 1.040 0.018
Capintec PR-06 1.032 0.047 1.039 0.011 1.034 0.046 1.051 0.019
Note: Uncertainties (one standard deviation) given include both statistical (type A) and
systematic (type B) values.
Source: From Reference [15]. With permission.
TABLE 3.7
A Comparison of Absorbed Doses to Water Obtained
with a PTW Ion Chamber Using Different Calibration
Methods in a 155-MeV Range Modulated Proton Beam
—calculated k
Q
2.21 0.11 Gy
—measured k
Q
2.23 0.06 Gy
—calculated k
Qp
2.21 0.05 Gy
2.20
0.11 Gy
Note: Uncertainties (one standard deviation) given include both statis-
tical (type A) and systematic (type B) values.
Source: From Reference [15]. With permission.
D
w
k
Q
(
)
D
w
k
Q
(
)
D
w
k
Qp
()
D
w
N
Dp
()
S
()
air
w
[]
Q
1
L
()
air
w
[]
Q
0
p
air
w
[]
Q
1
p
air
w
[]
Q
0
p
air
w
[]
Q
1
p
air
w
[]
Q
0
p
repl
p
wall
k
Q
p
S
()
air
w
[]
Q
1
L
()
air
w
[]
Q
0
----------------------------
en
()
wair,
D
w
M
u
N
K
en
()
wair,
k
k
st
p
disp
Ch-03.fm(part 1) Page 100 Friday, November 10, 2000 11:58 AM
Ionization Chamber Dosimetry 101
the reference point in the water phantom. If the energy-
angular response free in air is R(E,
), defined as the ratio
of the meter reading of the ionization chamber in air (for
photons of energy E and angle
between the chamber
axis and the incoming photon beam) and the air kerma at
the same position, the response R
w
of the chamber at the
reference position in the water phantom can be calculated
from [18]
(3.36)
where is the double differential energy–angu-
lar photon fluence distribution at the reference point in the
water, (
en,air
)(E) is the mass energy absorption coeffi-
cient for air, and d 2
sin
d
.
The energy-angular response of the chamber thimble
resulting from the angular measurements was fitted with
polynomes both with respect to the angle axis (between
0 and 90°) and with respect to the energy axis (from 30
to 170 keV). The total correction factor for the energy-
angular dependence of the response is given by
(3.37)
where R
air
is the response free in air for the same radiation
quality. It can be seen that R
air
is given by
(3.38)
where
R
a
(E) represents the measured response free in air
for photons perpendicular to the chamber axis (i.e., R
a
(E)
R(E,90)) and
E
(E) is the primary photon fluence spec-
trum, differential in energy, free in air. [18]
The behavior of the correction factors k
is completely
different from that of k
u
. It always exceeds unity and is
maximal in the region (at 80 keV mean energy) where the
contribution of scattered radiation, which is ignored in the
evaluation of k
u
, is maximal. However, the factor k
is
close to unity (1 k
1.015), due to the small number
of photons at solid angles close to
0.
When an ionization chamber is calibrated free in air,
its measured response is increased compared with the
situation without its stem. In order to undo the effect of
the stem on the chamber response free in air, a correction
factor smaller than unity must be applied to the response.
Suppose the reading of the chamber in air with the stem
is
M
s,a
and the reading of the chamber using an additional
dummy stem of similar material is M
ss,a
; then the correc-
tion factor required on the response to undo the stem effect
free in air is given by [18]
(3.39)
When the chamber is used for absorbed dose measure-
ments in a water phantom, the presence of the stem influ-
ences the number of scattered photons reaching the cham-
ber. A similar correction factor
k
s,w
can be defined for stem
effect in the phantom. The total stem correction for an
ionization chamber is given by
(3.40)
The free-in-air and the in-phantom stem effects are
cumulative, and the resulting correction factor therefore
exceeds unity by up to 1.5% at a mean energy of 50 keV.
It should be pointed out that, due to the asymmetric sen-
sitivity of the ionization chamber on both sides of the
thimble, the correction factor may be overestimated by up
to 0.5% at 30 keV mean photon energy according to Monte
Carlo calculations by Ma and Nahum. [19]
The displacement correction factor is calculated as
(3.41)
where
k
air,w
is the air kerma at the reference point in the
phantom and is the air kerma in the center of the
air-filled cavity at reference depth in the water phantom.
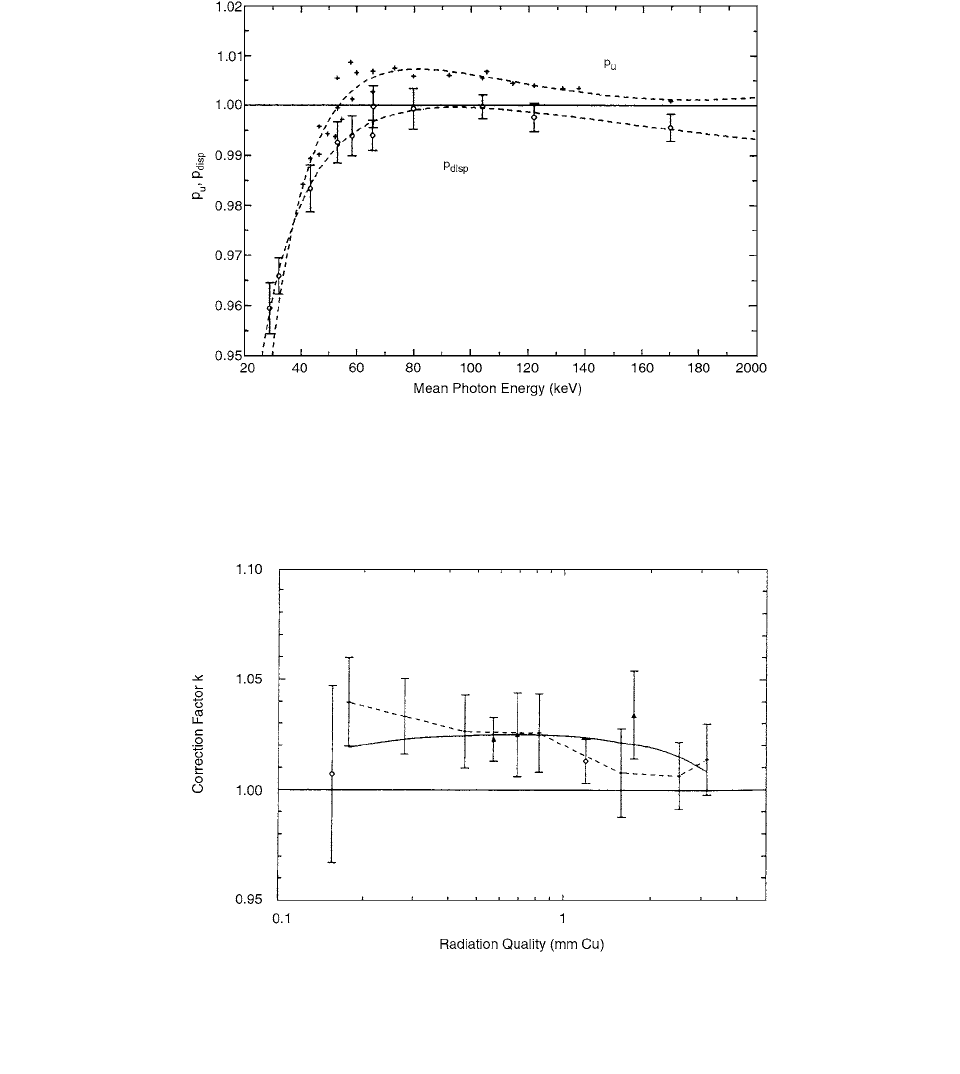
Figure 3.11 shows the results in comparison with the
previously published p
u
correction factors.
The overall correction factor k as a result of the
comparison water calorimeter with ionization chamber
measurements is plotted in Figure 3.12. The error bars
shown correspond with the total uncertainty as discussed
above (on a 1
level). Also shown in Figure 3.12 (by the
full curve) are the results of the determination of the
overall correction factor for the NE2571 ionization
chamber.
D. OTHER CORRECTION FACTORS
The air-kerma calibration factors for cylindrical or end-
window parallel-plate ionization chambers are usually
determined free in air, and the x-ray machine output is
stated as the air-kerma rate free in air, which, when mul-
tiplied with the appropriate backscatter factor, gives the
air-kerma rate on the surface of a phantom or patient. For
end-window chambers, especially when they are used for
measurements of small fields or low x-ray energies, the
air-kerma calibration factors may also be determined with
the chamber embedded in a tissue-equivalent phantom.
R
w
en air,
--------------
E()RE
,()
E ,
E
,()E E d d
0
E
max
en air,
--------------
E()
E ,
E
,()E E d d
0
E
max
---------------------------------------------------------------------------------------------------------------
E ,
E
,()
k
R
air
R
w
R
air
en air,
--------------
E()R
a
E()
E
E()E Ed
0
E
max
en air,
--------------
E()
E
E()E Ed
0
E
max
----------------------------------------------------------------------------------
k
sa,
M
sa,
M
ss a,
k
st
k
sw,
k
sa,
p
disp
K
air, w
K
air, w
K
air, w
Ch-03.fm(part 1) Page 101 Friday, November 10, 2000 11:58 AM
102 Radiation Dosimetry: Instrumentation and Methods
[21] This results in field-size dependent air-kerma in-air
calibration factors but obviates the requirement for knowl-
edge of backscatter factors when determining the air-
kerma rate on the surface of a phantom.
The body of these end-window chambers acts as a
mini-phantom which, at low and medium photon energies,
provides an inherent non-negligible scattering component,
making the measurement of exposure in air or air kerma
in free air with such a chamber problematic, especially
when radiation field sizes on the order of chamber cross-
sectional dimensions are used. [21]
The x-ray tube output, expressed as the air-kerma
rate (B) free in air, is usually obtained by multiplying
the appropriate N
K
(air-kerma calibration factor) provided
by the standards laboratory by the ionization chamber
signal M (measured in air per unit time for arbitrary field
FIGURE 3.11 Correction factor p
disp
(0) for the volume displaced by the chamber calculated for a cylindrical air cavity with its
center at 5 cm in a water phantom, its axis perpendicular to the radiation beam (a parallel beam of 15 cm diameter), and its dimensions
equal to the outer dimensions of the NE2571 chamber (i.e. 2.5-cm length and 0.35-cm radius). For comparison the former results
p
u
()[20] are shown. (From Reference [18]. With permission.)
FIGURE 3.12 Overall correction factor k for the NE2571 chamber derived from the comparison of water calorimetry with ionization
chamber dosimetry (broken curve) and as the result of the independent determination
k k
k
st
p
disp
by a combination of experimental
investigations and Monte Carlo calculations (full curve). The results of the work of Mattsson (1985) [17a] and Kubo (1985) [17b]
are shown by (O) and the (
), respectively. (From Reference [18]. With permission.)
K
˙
air
p
Ch-03.fm(part 1) Page 102 Friday, November 10, 2000 11:58 AM

Ionization Chamber Dosimetry 103
size B and corrected for temperature, pressure, and recom-
bination losses); i.e.,
(3.42)
For measurements with the cylindrical chamber, Equa-
tion (3.42) is valid irrespective of field size
B, provided
that the chamber stem effect, on the order of 1% for rec-
tangular fields with high elongation factors, is accounted
for. With the phantom-embedded end-window chamber,
on the other hand, the air-kerma rate in free air calculated
from Equation (3.42) is correct only for field sizes B
identical to field size A, which was used during the cali-
bration procedure in the standards laboratory. For arbitrary
field size B, the air-kerma rate in free air (B) can be
determined with the phantom-embedded end-window
chamber using the following relationship: [21]
(3.43)
where
M(B) is the chamber reading, corrected for temper-
ature, pressure, and recombination losses, and measured
with field size B; N
K
(A) is the in-phantom air-kerma cali-
bration factor provided for field A by the standards labo-
ratory; and BSF
air
(A)/BSF
air
(B) is the ratio of air
kerma–based backscatter factors for fields A and B.
For a given field size , the backscatter factor
BSF
air
(
) is defined as the ratio of the air-kerma rate on
the surface of the phantom to the air-kerma rate
free in air ; i.e.,
(3.44)
This is in contrast to water kerma-based backscatter factor
BSF
w
(
), which is defined as the ratio of the water-kerma
rate on the phantom surface to the water-kerma rate
free in air , or
(3.45)
For a given field size
, the two backscatter factors
BSF
air
(
) and BSF
w
(
) are related through the following
expression:
(3.46)
where is the ratio of mass-energy absorp-
tion coefficients for water and air, averaged over the photon
energy fluence spectrum present on the phantom surface S
for field
, and is the ratio of mass-energy
absorption coefficients for water and air evaluated over
the primary x-ray energy fluence spectrum in air. [21]
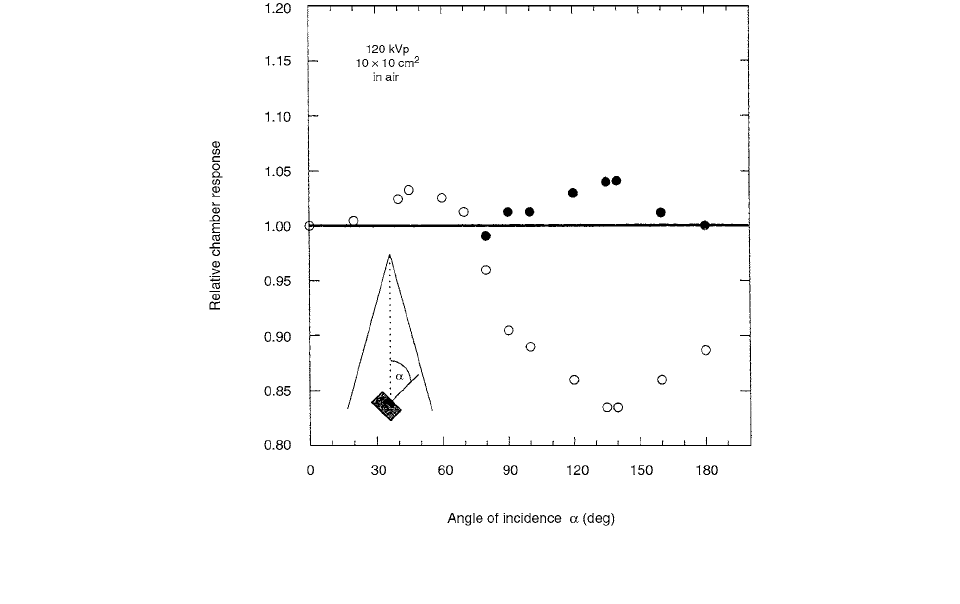
The results for an x-ray effective energy of 34 keV
(120kVp) are presented in Figure 3.13. Angle
0°
corresponds to normal incidence, with the beam imping-
ing directly onto the polarizing electrode, and
180°
corresponds to normal incidence with the beam traversing
the body of the chamber.
In superficial and orthovoltage radiotherapy, the air-
kerma rate determined free in air is only of secondary
importance. It is the dose rate on patient’s surface obtained
for a given field size B which plays the most important
role in dose delivery and radiation dosimetry.
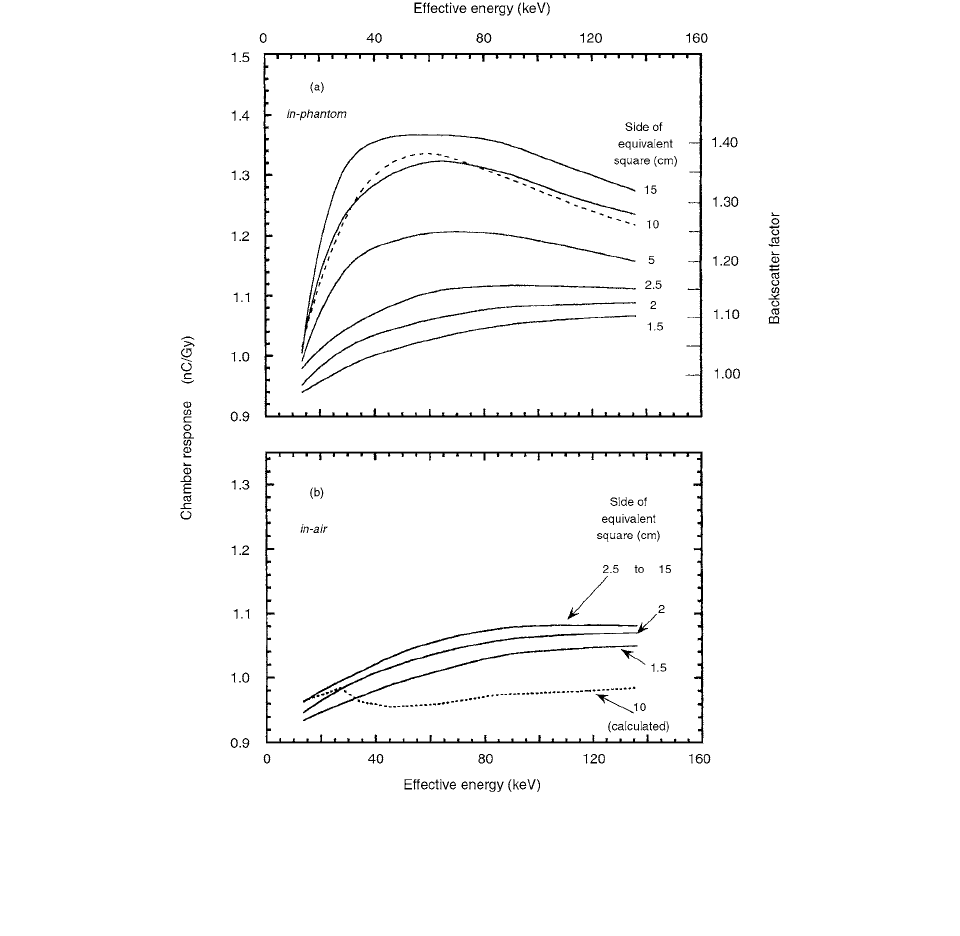
It is shown in Figure 3.14a that the chamber response
measured in phantom depends on beam energy and field
size in an expected fashion. In Figure 3.14b the chamber
response measured in air follows the expected behavior
for fields above 2.5
2.5 cm
2
, showing that for a given
beam energy, the chamber response is essentially indepen-
dent of field size. For a given beam energy and fields
smaller than 2.5 2.5 cm
2
, however, the chamber exhibits
a field size dependence, with the in-air chamber response
decreasing with field size, indicating that the scatter from
the chamber body has an effect on the chamber reading,
the effect diminishing with a decreasing field size.
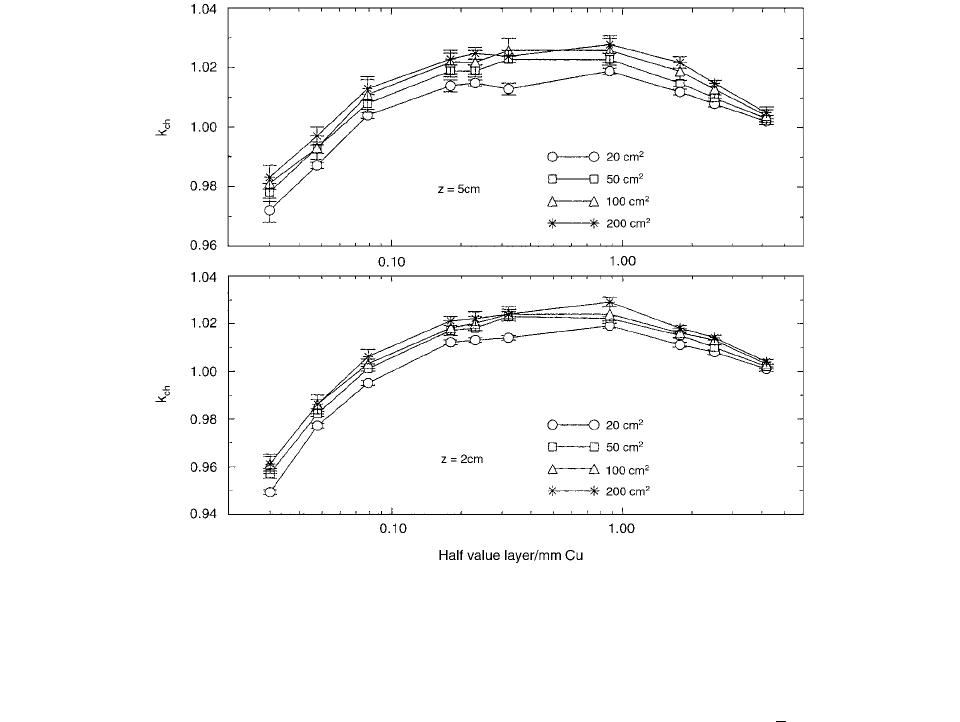
Seuntjens and Verhaegen [22] examined the depth and
field size dependence of the overall correction factor k
ch
for in-phantom dose determinations in orthovoltage x-ray
beams. The overall correction factor is composed of three
contributions: a contribution from the angular dependence
of the chamber response free in air, derived from the mea-
sured directional response of the NE2571 for different
energies combined with Monte Carlo calculations; a dis-
placement effect; and a stem effect. The displacement effect
and stem effect are both calculated using the Monte Carlo
method for different field sizes and depths. The results
show a variation of, at most, 2.2% at the lowest photon
energies (29.8-keV average photon energy) when going
from 2 to 5 cm for a small circular 20-cm
2
field. In the
medium-energy range (100 kV), variations are limited
to, at most, 1.5% for 120 kV–150 kV when comparing
the most extreme variations in field size and depth
(i.e., 2-cm depth; 20-cm
2
area compared to 5-cm depth;
200-cm
2
area). Depth variations affect the overall correc-
tion factor most significantly by hardening of the photon
fluence spectrum, whereas field diameter variations affect
the factor by increase or decrease of contributions of pho-
ton scattering.
Absorbed dose to water is determined using the equa-
tion
(3.47)
K
˙
air
p
B() MN
k
K
air
p
K
˙
air
p
B() MB()N
K
A()
BSF
air
A()
BSF
air
B()
------------------------
K
air
s
()
K
air
p
()
BSF
air
()
K
˙
air
s
()
K
˙
air
p
()
------------------
K
w
s
()
K
w
p
()
BSF
w
()
K
w
s
()
K
w
p
()
----------------
BSF
w
()
BSF
air
()
------------------------
ab
()
air
w
[]
S
,
ab
()
air
w
[]
p
-----------------------------------
ab
/
()
air
w
[]
S
,
ab
/
()
air
w
[]
p
D
w
MN
K
en
--------
w,air
k
ch
Ch-03.fm(part 1) Page 103 Friday, November 10, 2000 11:58 AM
104 Radiation Dosimetry: Instrumentation and Methods
where M represents the chamber reading at depth z in
water corrected for temperature, pressure and recom-
bination; (
en
/
)
w,air
represents the mass energy absorption
coefficient ratio of water to air averaged over the photon
fluence spectrum at the point of measurement at a depth
in water; and k
ch
represents the overall correction factor,
incorporating all changes in chamber response between
the calibration in air at the standards laboratory and the
in-phantom measurement in the user’s beam. Using Monte
Carlo simulations, there are three practical methods to
infer an overall correction factor for medium-energy x-ray
beams. The first method is the direct calculation of k
ch
as
the quotient of the in-water to in-air kerma ratio and the
in-water to in-air chamber reading ratio in a correlated
sampling process, including electron transport, as per-
formed by Ma and Nahum: [23]
(3.48)
where and represent the air-kerma in phantom
at the point of measurement and the air-kerma free in air,
respectively, and and (calculated) represent
chamber doses in phantom and free in air, respectively. The
disadvantage of this method is the enormous computing
time required to generate acceptable statistical uncertain-
ties for the in-phantom calculations.
A second method employs the same concept but uses
measurements of the chamber readings in phantom (M
w
)
to free in air (M
a
) as opposed to the Monte Carlo calcu-
lations of these quantities such as in the previous method.
When deriving absolute values of the overall correction
factor k
ch
, this method suffers from problems associated
with the exact knowledge of the low-energy tail of the
photon fluence spectrum that significantly contributes to
calculated air kerma free in air, but not to the calculation
of kerma at depth in the phantom. However, the variation
of the overall correction factor for a different field size
(d) and/or depth (z) relative to the value at the standard
conditions (d, z) can be derived from: [22]
(3.49)
A third successful method of inferring the overall cor-
rection factor is based on an experimental study of the
combined angular-energy (or directional) response of a
cylindrical chamber, a Monte Carlo calculation of the pho-
ton fluence distribution differential in energy and angle at
the reference depth in the phantom, a separate Monte Carlo
calculation of the effect of the displaced volume, and a
measurement of the stem effect in air and in phantom.
FIGURE 3.13 End-window chamber response vs. the angle
of the incident beam; raw data (open circles) and data corrected for
chamber attenuation (solid circles). (From Reference [21]. With permission.)
k
ch
K
air
w
K
air
a
--------
D
cav
w
D
cav
a
---------
K
air
w
K
air
a
D
cav
w
D
cav
a
k
ch
z d,()
k
ch
zd,()
-------------------------
K
air
w
z d,()
K
air
w
zd,()
---------------------------
M
w
zd,()
M
w
z d,()
--------------------------
Ch-03.fm(part 1) Page 104 Friday, November 10, 2000 11:58 AM
Ionization Chamber Dosimetry 105
The values shown in Figure 3.15 are obtained repre-
senting the overall correction factor for the two depths and
for field areas varying between 20 and 200 cm
2
. The error
bars shown in this figure represent the combined statistical
errors of the Monte Carlo calculations only and disregard
any systematic effects.
Absorbed dose values determined with the commonly
applied NACP and PTW/Markus parallel-plate chambers
and the cylindrical NE2571 Farmer chamber were com-
pared by Van dell Plaetsen et al. [24] to values obtained
with ferrous sulphate dosimetry in a number of electron
beams. For the ionometry with the parallel-plate cham-
bers, the dose-to-air chamber factor N
D
(or N
gas
) was derived
from a
60
Co-beam calibration free in air with an additional
buildup layer of 0.54 g cm
2
graphite, as proposed by the
protocol for electron dosimetry published by the Nether-
lands Commission on Radiation Dosimetry. The behavior
of the fluence perturbation correction factor p
f
vs. the mean
electron energy at depth was deduced for the flat
PTW/Markus and cylindrical NE2571 chamber by com-
parison with the NACP chamber, for which p
f
was
assumed unity. The results show a small but significant
energy dependence of p
f
for the PTW/Markus chamber.
For cylindrical chambers, N
D
(or N
gas
) can be derived
directly from the air-kerma calibration factor N
K
, deter-
mined free in air against the national standard in a beam
FIGURE 3.14 Parallel-plate end-window chamber response (solid curves) normalized to an in-air dose of 1 Gy in the effective beam
energy range from 10 to 140 keV for various square fields in the range from 1.5
1.5 cm
2
to 15 15 cm
2
. Part (a): chamber response
in phantom; part (b): chamber response in air. The dashed curve of (a) represents the backscatter factor for a 10
10-cm
2
field; the
dotted curve of (b) represents the chamber response calculated with Equation (3.43) from the measured data given for a 10
10-
cm
2
field in (a). (From Reference [21]. With permission.)
Ch-03.fm(part 1) Page 105 Friday, November 10, 2000 11:58 AM
106 Radiation Dosimetry: Instrumentation and Methods
of
60
Co gamma-rays, using the expression
(3.50)
Here k
m
is a correction for the nonair equivalence of the
chamber wall and buildup materials and k
cel
is a correction
for the nonair equivalence of the central electrode. k
att
represents the correction for attenuation and scatter of the
photon beam in the ionization chamber during calibration.
With the known N
D
factor, the absorbed dose to water
in the electron beam at the effective point of measure-
ment in the phantom material can be determined with the
equation
(3.51)
In this expression p
wall
represents a correction for the dif-
ference in composition between the chamber and phantom
materials, p
d
is a correction for the difference in ionization
at the effective point of measurement and the depth at
which the absorbed dose is stated, and P
cel
is a correction
for the difference in composition between the central elec-
trode and the phantom material. The fluence perturbation
correction factor p
f
accounts for the imbalance between
the number of electrons scattered from adjacent phantom
material into the air cavity and the number of electrons
scattered by the air cavity.
The fluence perturbation factor p
f
of the parallel-plate
PTW/Markus chamber is presented in Figure 3.16. In this
figure p
f
is given as a function of , the mean energy at
the depth of the effective point of measurement, which is
the depth of dose maximum for the electron beams.
Sometimes there are significant differences in temper-
ature between the chamber and measurement phantom. To
obtain reliable ionization data, the temperature of the air
in the chamber must be allowed to equilibrate with the mea-
suring phantom. The air temperature inside a thimble of a
Farmer-type ion chamber was measured by Tailor et al. [25]
as a function of time for various phantom materials (air,
water, and plastic). In each case, temperature difference is
plotted vs. time on a semi-log scale. Distinct differences
between the different types of media in the thermal equil-
ibration are noted and discussed. Negligible differences
were seen between conductive or nonconductive thimble
material and between heating and cooling rates. The ther-
mal-equilibration curves are verified by heat-diffusion the-
ory. Further, the temperature measurements are confirmed
by ionization measurements in a plastic medium.
Let the time after zero time be denoted as t, the tem-
perature difference between the ‘‘chamber” and the phan-
tom be T, the initial temperature difference be T
0
, and
the initial phantom temperature be T
0
. Data are presented
as semi-log plots of the normalized temperature differ-
ence, T/T
0
, vs. time.
FIGURE 3.15 Overall chamber correction factor k
ch
for the NE2571 ion chamber, representing the combination of all three compo-
nents. Upper panel represents data at 5-cm and lower panel at 2-cm depth. (From Reference [22]. With permission.)
N
D
N
K
1 g()k
att
k
m
k
cel
D
w
P
eff
() MN
D
s
w air,
p
wall
p
d
p
f
p
cel
E
z
Ch-03.fm(part 1) Page 106 Friday, November 10, 2000 11:58 AM
Ionization Chamber Dosimetry 107
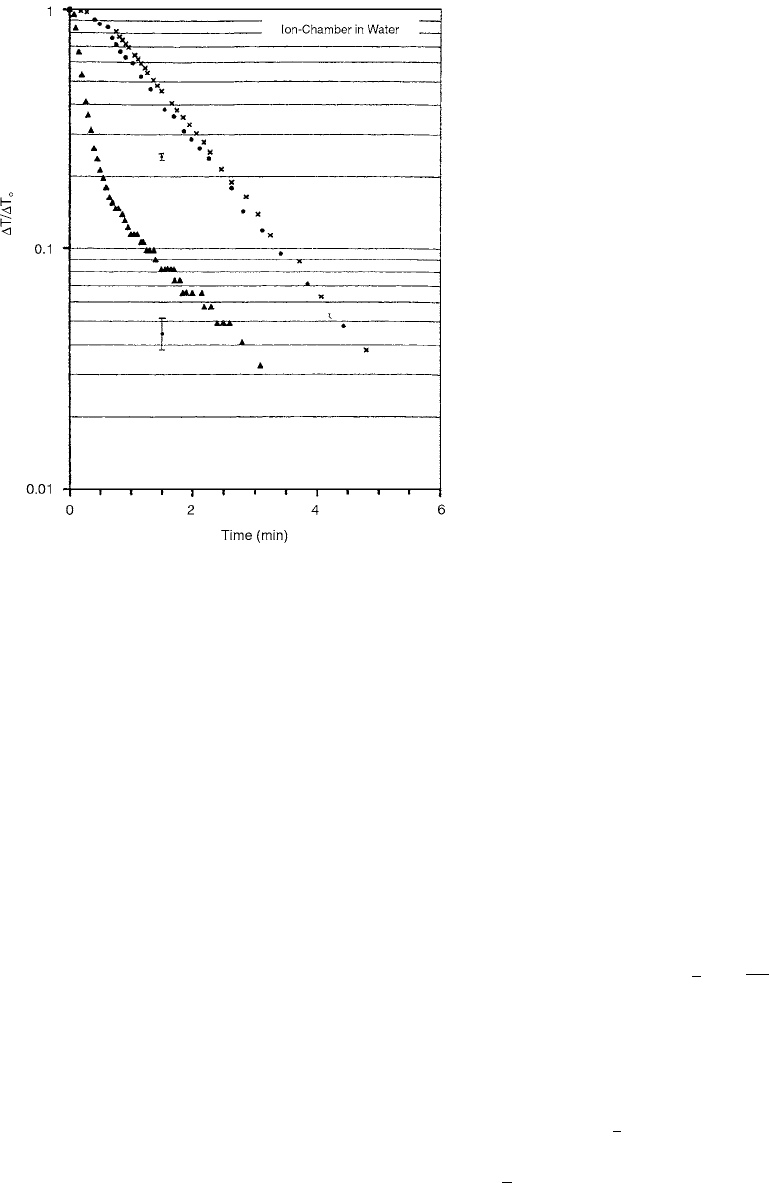
The data in Figure 3.17 represent thermal equilibration
of a Farmer-type ion chamber in air. The solid-circle sym-
bols represent warming of the chamber and build-up cap
in air. The initial shoulder (width 0.5 min) represents
a delay in heat transmission through the 0.46-cm Lucite
wall of the build-up cap. The shoulder is followed by
a single-exponential fall-off; ionization measurements were
made in a
60
Co-beam with a similar ion chamber and build-
up cap cooling in air. The change in ionization readings
was then used to deduce the change in temperature of the
air inside the thimble using the ideal gas law. The cross
symbols in Figure 3.17 represent the ionization data con-
verted to temperature-change data. The ionization and
the direct temperature measurements are in excellent
agreement. The solid-triangle symbols represent cooling
of the chamber with a bare thimble in air. The absence of
the shoulder in these data indicates a negligible delay in
heat transmission through the thimble because of negligi-
ble wall thickness (0.036-cm nylon). As expected, tem-
perature equilibration is much faster because there is no
build-up cap. These data show more than a one-component
exponential fall-off. The initial fall-off, until T reaches
close to 10% of T
0
, is a fast component, whereas the latter
fall-off is much slower and perhaps arises from continua-
tion of heat transfer from the stem of the chamber. The
stem, because of insulating contents and large heat capacity,
takes longer to equilibrate with the surrounding air.
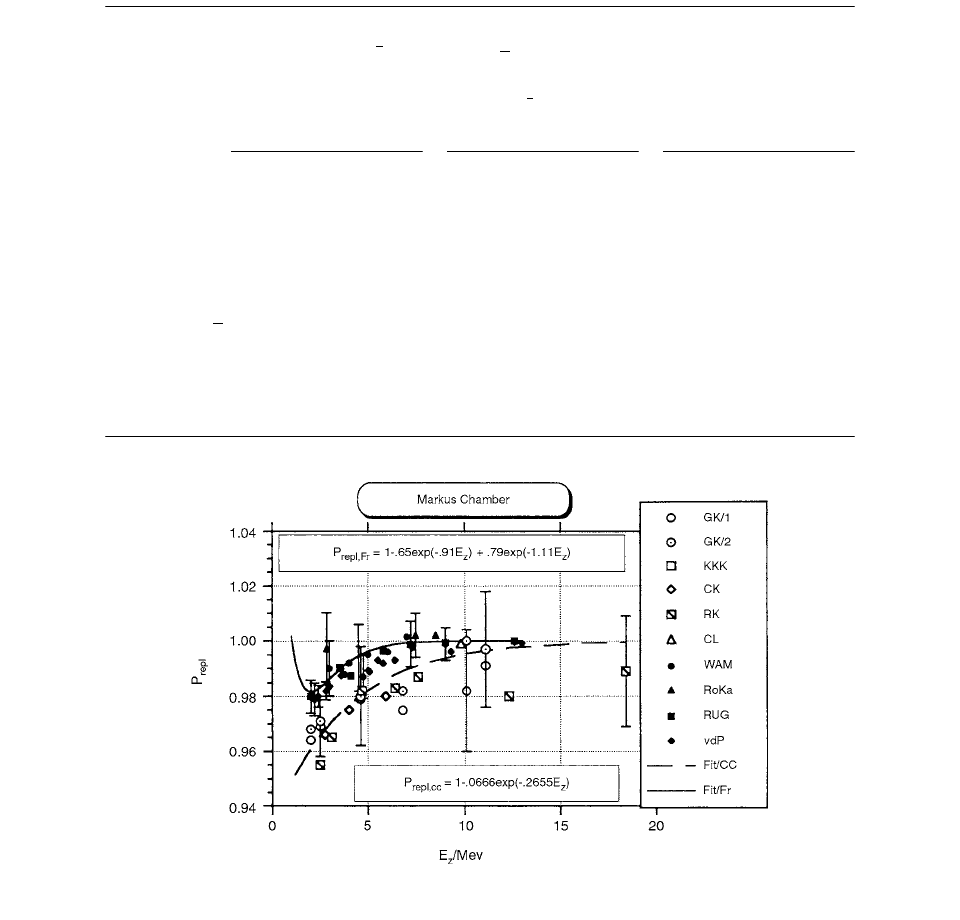
The data in Figure 3.18 represent thermal equilibration
of an ion chamber in a water phantom. The solid circle
and cross symbols represent cooling and warming data,
respectively, when the chamber, along with its build-up
cap, are inserted into the water phantom. The two sets of
data corresponding to warming and cooling are in good
agreement within measurement error. The initial shoulder,
representing a delay in heat transmission through the
0.46-cm Lucite wall of the build-up cap, is followed by a
single-component exponential fall-off similar to that of
the chamber with build-up cap in Figure 3.17. Equilibra-
tion is about five times faster in water than in air. The
solid-triangle symbols represent the data for insertion of
the ion chamber’s bare thimble into a build-up cap already
FIGURE 3.16 The fluence perturbation correction factor p
f
vs. the mean electron energy at depth for the PTW/Markus chamber.
The error bars represent 1 s.d. The full line is the result of a fit to the data of the functional form
p
f
1A exp(B ) with
the values of the coefficients A
0.039 and B 0.2816MeV
1
. (From Reference [24]. With permission.)
E
z
E
z
FIGURE 3.17 Cooling/warming curves for an ion chamber in
air. No build-up cap (
), build-up cap warming (O). (From
Reference [25]. With permission.)
Ch-03.fm(part 1) Page 107 Friday, November 10, 2000 11:58 AM
108 Radiation Dosimetry: Instrumentation and Methods
at thermal equilibrium in the water phantom. The initial
shoulder is absent, as exhibited previously by the bare-
thimble data in Figure 3.17. The second exponential com-
ponent is again probably attributable to the influence of
the stem. [25]
TG-21 states that c-chambers should be avoided for
electron-beam energies below 10 MeV. [26] From the
Dutch protocol, a limit of about 6 MeV can be deduced.
Two criteria are given for the choice of a pp-chamber: a
‘‘position criterion’’ related to the poor definition of the
effective point of measurement of c-chambers, quoted
to be between 0.3 and 0.7 of the inner chamber radius in
front of the chamber center, and an ‘‘energy criterion”
related to the consistency of dose determination with both
chamber types. At least two more concerns with c-cham-
bers at low electron energies become obvious from a look
at a typical low-energy electron depth dose curve: the
effective point of measurement, usually derived at the
steep part of the depth dose curve, may be different near
the peak dose and may be dependent on energy as well
as position; and, even assuming that the effective point of
measurement would be known exactly, the meaning of
a measured maximum chamber response remains uncer-
tain because of the relatively large chamber diameter
which results in an underestimation of the true maximum
dose at positions around peak-dose depth rather than at
the descending part of the depth dose, where a good
average will be derived. In addition, electron fluence will
be disturbed in an uncontrollable way. TG-21 ignores the
effect of the central electrode in c-chambers which may
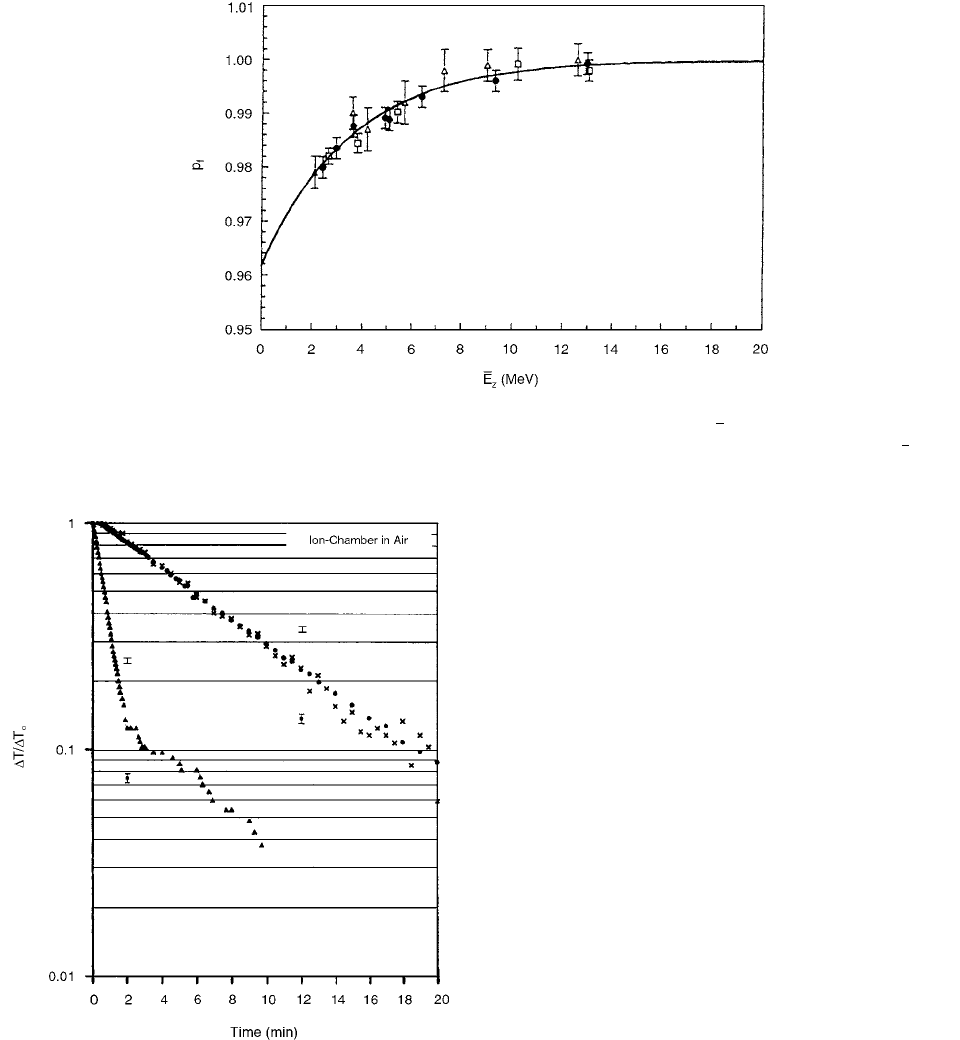
be distinct at low-electron energies. [26]
In Figure 3.19 measurements are compiled after mod-
ification, where necessary, to allow for plotting them over
the effective energy at depth of measurement. There
appears to be a drop of P
repl,pp
for the Markus chamber
from unity at high energies by about 3 to 5% at the low-
energy end (Figure 3.19, open symbols). Interestingly, this
drop results in cases where the comparison is made
to c-chambers by the same (insufficient) methodology.
Wittkamper et al. have derived P
repl,pp
from a comparison
to Fricke dosimetry. Their results agree with ours, also
derived with Fricke dosimetry, and both show a clearly
different result (Figure 3.19, solid symbols). The devia-
tion of P
repl,pp
from unity at low energies is within mea-
surement accuracy, although there is some indication of
a deviation from unity, as shown by the experimental
points. Van der Plaetsen et al. [24] found the mean value
for this chamber to be 0.8% higher than unity over the
full-energy range in question, which would confirm a
relative difference between the Markus and the NACP
chambers. [26]
E. MONTE CARLO CALCULATED CORRECTION
Ion-chamber responses were calculated for graphite,
PMMA, and aluminum-walled ion chambers free in air in
60
Co beams and 200-keV beams for a graphite chamber
by Rogers. [27] The EGS4 Monte Carlo system was used
with various electron step-size algorithms, in particular
the PRESTA algorithm, the much simpler ESTEPE con-
straint on the energy loss per step, and in combination.
Contrary to previous reports, it was found that there are
variations in the calculated ion-chamber response of up to
3% in
60
Co beams and up to 8% in the 200-keV beam.
According to Spencer-Attix cavity theory, the dose to
the air in the cavity per unit air kerma at the midpoint of
the chamber in the absence of the chamber is given by
(3.52)
where
D
air
is the dose to the air, K
col,air
is the air-collision
kerma at the center of the ion chamber in the absence
of the chamber, K
wall
is the correction for wall attenuation
and scatter, is the Spencer-Attix stopping-
power ratio for an energy threshold of 10 keV, and
is the ratio of mass-energy coefficients for the
wall to air. This expression is the fundamental equation
used for primary standards of air kerma in
60
Co beams.
The right-hand side can be evaluated with negligible sta-
tistical uncertainty. Table 3.8 and Figure 3.20 show cal-
culated values of k
m
.
FIGURE 3.18 Cooling/warming curves for an ion chamber in
a water phantom. No build-up cap (
), lucite build-up cap cooling
(X) and warming (O). (From Reference [25]. With permission.)
D
air
K
wall
K
col, air
--------------------
L
---
wall
air
en
-------
air
wall
k
m
L/
()
wall
air
en
/
()
air
wall
Ch-03.fm(part 1) Page 108 Friday, November 10, 2000 11:58 AM
Ionization Chamber Dosimetry 109
Ma and Nahum [28] calculated the stem-effect cor-
rection factors for the NE2561 and NE2571 ionization
chambers calibrated in air and used at a depth in a phantom
irradiated by medium-energy x-ray beams. The in-air and
in-phantom stem effect correction factors were calculated
as the ratios of the absorbed dose in the air cavity of an
ionization chamber with and without a chamber stem. The
‘‘global” stem correction factor was then calculated as the
ratio of the in-phantom correction factor to the in-air cor-
rection factor. The results show that, in general, the cham-
ber stem increases the chamber response in air but
decreases it in phantom.
The global stem effect correction factor,
k
stem,global
, is
defined as the ratio of the in-water stem correction fac-
tor, k
stem,water
, to the in-air stem correction factor, k
stem,air
;
i.e.,
(3.53)
The variation of the stem-effect correction with SSD
for an NE2561 chamber irradiated at 3-cm depth in water
by a point source of a 100-kV photon beam is shown in
Figure 3.21.
The magnitude of the stem effect depends strongly on
the beam field size. As is shown in Figure 3.22, for an
NE2561 chamber irradiated at 3-cm depth in water by a
point source of a 100-kV photon beam with a 50-cm SSD,
the stem correction factor increases with field radius (
R)
and stabilizes for R 4 cm. The global factor k
stem,global
for an NE2561 chamber is 1.034 0.002 for R 5 cm
but decreases to 1.013 0.002 for R 1cm.
TABLE 3.8
Values in
60
Co Beams of k
m
, , and
k
m
1.25 MeV
60
Co 1.25 MeV
60
Co 1.25 MeV
60
Co
Graphite 1.0006 1.0009 0.9993 0.9979 0.9999 0.9988
PMMA 1.0805 1.0800 0.9080 0.9075 0.9811 0.9801
Aluminum 0.9615 0.9629 1.1602 1.1606 1.1156 1.1176
Note: Calculated using EGS4 photon data sets and the electron stopping powers of ICRU Report 37. The stopping-
power ratios were calculated for electron spectra in the center of small mini-phantoms of the appropriate material.
The values of are 5.337 10
12
and 4.554 10
12
Gy cm
2
for the 1.25-MeV photons and the
60
Co
beam, respectively. Bremsstrahlung losses were 0.32% for graphite and PMMA and 0.7% for aluminum. The one-
standard-deviation statistical uncertainties in the Monte Carlo calculations were less than 0.1% in all cases.
Source: From Reference [27]. With permission.
FIGURE 3.19 Compilation of P
repl,pp
values from the literature. (From Reference [26]. With permission.)
L/
()
wall
air
en
/
()
air
wal
l
en
---------
air
wall
L
---
wall
air
en
/
()
ai
r
k
stem, global
k
stem, water
k
stem, air
Ch-03.fm(part 1) Page 109 Friday, November 10, 2000 11:58 AM
