Shani G. Radiation Dosimetry: Instrumentation and Methods
Подождите немного. Документ загружается.

60
Radiation Dosimetry: Instrumentation and Methods
by Chiu-Tsao et al. (using a MORSE Monte Carlo code),
and by Luxton (using an EGS4 code and assuming a point
source model).
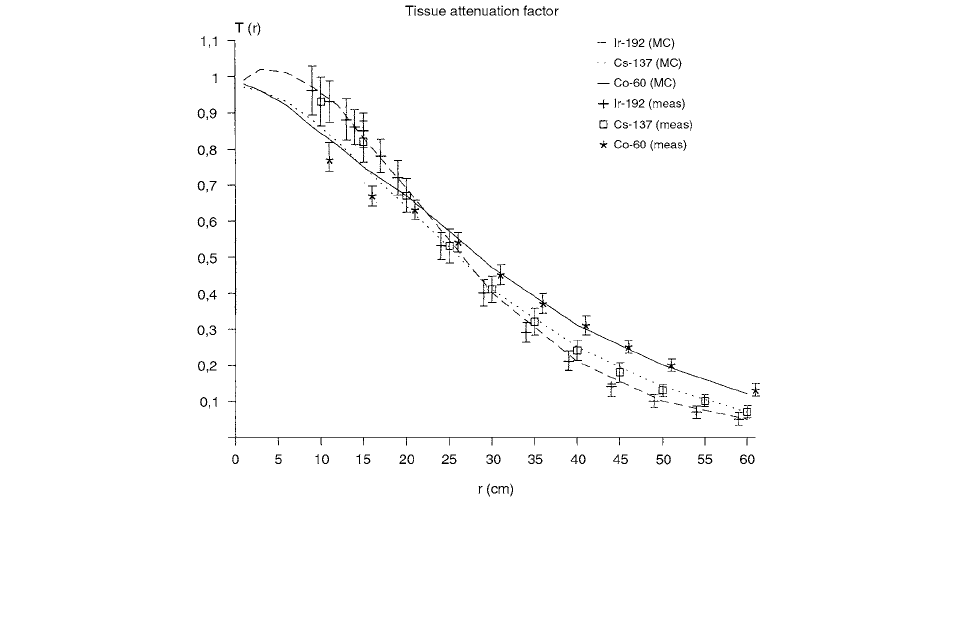
In order to describe the decrease of dose with distance,
ionization chamber measurements were performed by
Venselaar et al. [43] for the
60
Co,
192
Ir and
137
Cs sources in
a water tank. Source and chamber could be moved inde-
pendently. Dimensions of the water tank were changed to
simulate different patient sizes. As an independent check
of the results, Monte Carlo (MC) calculations with the
EGS-4 code system were performed in a simulated water
phantom. Using these results, a mathematical model was
used to describe the dose at large distances (10–60 cm),
which can be applied in addition to the existing calculation
models for the short range (
10 cm).
The decrease of the dose around a brachytherapy
point source is described mainly by the inverse square
law. Within the first few centimeters, a calculation of the
dose with only the inverse square law correction is accu-
rate within a few percent for medium- and high-energy
sources. However, deviations occur and these are due to
the additional contribution to the dose from scattered
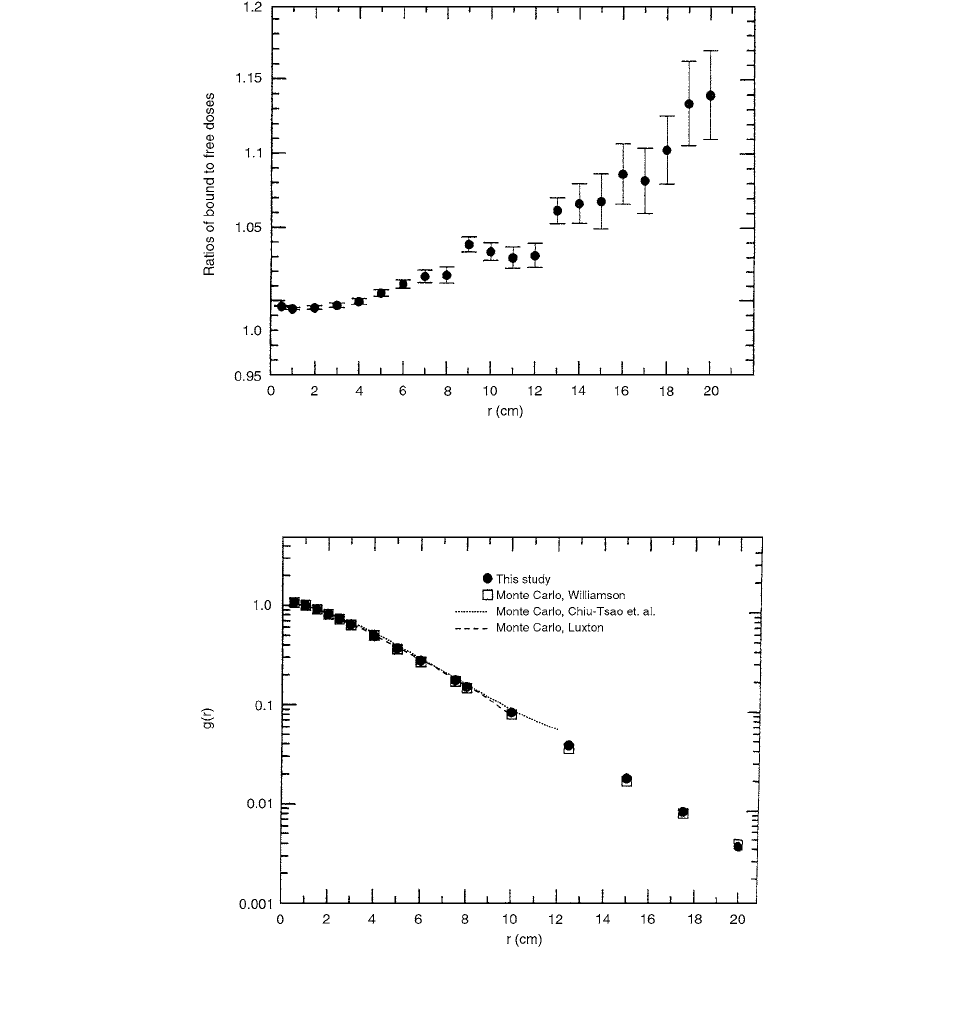
FIGURE 2.42
Influence of binding correction for Compton scattering on calculated doses for an
125
I 6711 source in water. The ratio
of doses with and without the correction is plotted as a function of distance on transverse axis. (From Reference [42]. With permission.)
FIGURE 2.43
Calculated radial dose function for an
125
I Model 6711 source in unbounded water compared with Monte Carlo results.
(From Reference [42]. With permission.)
Ch-02.fm Page 60 Friday, November 10, 2000 10:53 AM
Theoretical Aspects of Radiation Dosimetry
61
radiation and from absorption of radiation. At 10 cm,
deviations from the inverse square law may be as large
as 20%, depending on the energy of the emitted radiation.
The scatter and absorption effects are usually taken into
account in a combined “tissue attenuation factor,”
T
(
r
),
in order to calculate the dose rate as a function of
the distance
r
from the assumed point source:
(2.162)
When
S
is taken to account for the air-kerma strength
of the source expressed in the units
Gy m
2
h
1
and
r
in
cm, the dose rate is in cGy h
1
. For , the
average mass energy absorption coefficient, the value
1.112 may be inserted for the sources
137
Cs,
192
Ir, and
60
Co.
T
(
r
) in this equation is traditionally written as the ratio of
exposure in water to exposure in air or as a ratio of dose
in water to water kerma in free space.
For monoenergetic radiation, an expression can be writ-
ten on a more fundamentally physical basis:
T
(
r
)
B
(
r
)
exp(
r
), in which
B
(
r
) can be interpreted as a
buildup factor and
as the linear attenuation coefficient
in water. In many cases the isotopes used as brachytherapy
sources have a complex spectrum.
B
as a function of
r
has
to be parametrized, so the advantage as a physically
acceptable model is limited. The mathematical expression
used is
(2.163)
Tripathy and Shanta [44] have further developed this
approach and presented a model with
T
(
r
)
.
. Its validity is reported again for the same iso-
topes in the range up to 30 cm.
The measurement equipment consisted of a water tank
with dimensions 100
50
35 cm
3
, in which a source
holder and an ionization chamber could be moved inde-
pendently. Absolute dose was measured with two ioniza-
tion chambers, one calibrated chamber with a sensitive
volume of 0.6 cm
3
(graphite, NE 2505/3) and one with a
35-cm
3
volume (NE 2530). The chambers were connected
to a NE Ionex 2500/3 electrometer.
In Figure 2.44 the results of the measurements and
the calculations for an “infinitely” sized phantom are pre-
sented together for the three isotopes. Points are used for
the measurements in the range of 10–60 cm. Error bars
indicate the estimated inaccuracy (1 sd) of the data points.
Lines are used for the representation of the Monte Carlo
results in the range of 1–60 cm.
A dose calculation algorithm for brachytherapy was
presented by Russell and Ahnesj [45] that reduced errors
in absolute dose calculation and facilitates new techniques
for modelling heterogeneity effects from tissues, internal
shields, and superficially positioned sources. The algorithm
is based on Monte Carlo simulations for specific source
and applicator combinations. The dose is scored separately,
in absolute units, for the primary and different categories
of scatter according to the photon scatter generation.
FIGURE 2.44
Results of the measurements and the calculations for an “infinitely” sized phantom, presented together for
192
Ir,
137
Cs,
and
60
Co. Results in the range of 10–60 cm obtained by measurement are presented as points; the error bars indicate the estimated
inaccuracy (1 sd) of the data points. Lines are used for the representation of the Monte Carlo results in the range of 1–60 cm. (From
Reference [43]. With permission.)
D
˙
r()
D
˙
r() S
K
en
()
a
w
Tr()r
2
D
˙
r()
en
()
a
w
Tr() 1 ka
r()
kb
[]
r()exp
a
1
a
2
r()
E
av
b1 b2 r()
Ch-02.fm Page 61 Friday, November 10, 2000 10:53 AM
62 Radiation Dosimetry: Instrumentation and Methods
Radial dose distributions for the primary dose and the
total scatter dose are parametrized using functions based
on simple one-dimensional transport theory. The fitted
radial parameters are functions of the angle to the long
axis of the source to account for the anisotropy of the dose
distribution.
denotes the calculated dose per radiant
energy to a point at the position
pos in a large water
phantom. The calculated dose rate to this point
from a single radioactive source is then
(2.164)
where the exponential corrects for the decay of the source
during the time
T and
is the source-specific radioactive
decay constant. The calculated kerma-per-radiant energy
in air at the reference point, , is used together
with the measured air-kerma rate in air, , at the same
reference point to determine the absolute dose rate. Since
includes the effects of attenuation and scatter
in air, the measured reference air-kerma rate must also
include these effects. This procedure eliminates the need
for correction factor (and associated errors) for the atten-
uation and scatter in air.
The dose to a point at radial distance r and angle
is
often defined as
(2.165)
where , the reference air-kerma strength
at radial distance in free space (
C is a
correction factor for converting kerma in air to kerma in
free space by accounting for attenuation and scattering in
air); is a standard point located 1 cm along the
perpendicular bisector (1,
/2);
is the specific dose rate constant;
F(r,
) is the anisotropy distribution describing the angular
dependence of the absorption and scatter in the source and
surrounding material; G(r,
) is the 1/r
2
geometry distribu-
tion including effects for the spatial distribution of the
source; g(r) is the radial dose profile along the perpendicular
bisector of the source; and e
T
is the correction for
exponential decay between the date of source calibration
and the treatment date. Equation (2.164) may be rewritten as
(2.166)
and by comparing Equations (2.165) and (2.166), one
finds that
(2.167)
and
(2.168)
where all the effects of the source, encapsulation, and
applicator on the dose distribution are implicit in the Monte
Carlo dose deposition kernel.
The total dose per radiant energy is the sum of the
primary and scatter dose contributions (all generations).
(2.169)
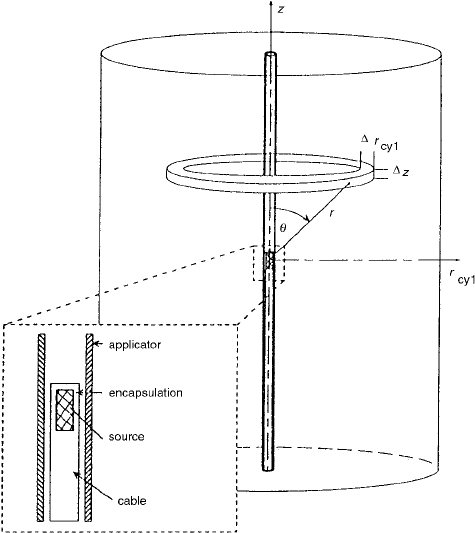
The EGS4/PRESTA computer code was used together
with a cylindrical scoring geometry to generate dose distri-
butions in a large homogeneous water phantom. The source
description and calculation model are shown in Figure 2.45.
An example of the dose deposition for a Monte Carlo
simulation of the
192
Ir source, described above, centered
in a nylon catheter with an outer diameter of 1.7 mm and
FIGURE 2.45 The cylindrical scoring geometry for the Monte
Carlo calculations. The water or air phantom is divided into a
number of rings of thickness
z and radial width . The
dose to points within the voxel is estimated as the total energy
absorbed by the ring divided by the mass of the ring. The details
of the source geometry are shown in the inset. Each shaded area
is treated as a separate region of medium in the Monte Carlo
calculations. The scoring volume is centered in a large volume
to simulate infinite-phantom conditions. (From Reference [45].
With permission.)
r
cyl
DR[]
c
wpos,
D
˙
c
w, pos
D
˙
c
wpos,
K
˙
m
aref,
D/R()
c
wpos,
K/R()
c
aref,
--------------------------
e
T
K/R()
c
aref,
K
˙
m
aref,
K/R()
c
aref,
D
˙
r
,() S
K
0
Gr
,()
Gr
0
0
,()
----------------------
Fr
,()gr()e
T
S
K
K
m
aref,
Cr
100
2
r
100
100 cm
r
0
0
,()
0
Dr
0
0
,()S
K
Dr
0
0
,()/ K
m
aref,
Cr
100
2
D
c
wpos
,
K
m
aref
,
Cr
100
2
D/R[]
c
w
, r
0
0
,()
K/R[]
c
aref
,
Cr
100
2
-------------------------------------
D/R[]
c
wpos
,
D/R[]
c
wr
0
0
,(),
-------------------------------
e
T
0
DR[]
c
wr
0
0
,(),
KR[]
c
aref
,
Cr
100
2
-------------------------------------
Gr
,()
Gr
0
0
,()
----------------------
Fr
,()gr()
DR[]
c
wpos,
DR[]
c
wr
0
0
,(),
-------------------------------
DR[]
c
wpos,
DR[]
c prim,
wpos,
DR[]
c scat,
wpos,
Ch-02.fm Page 62 Friday, November 10, 2000 10:53 AM
Theoretical Aspects of Radiation Dosimetry 63
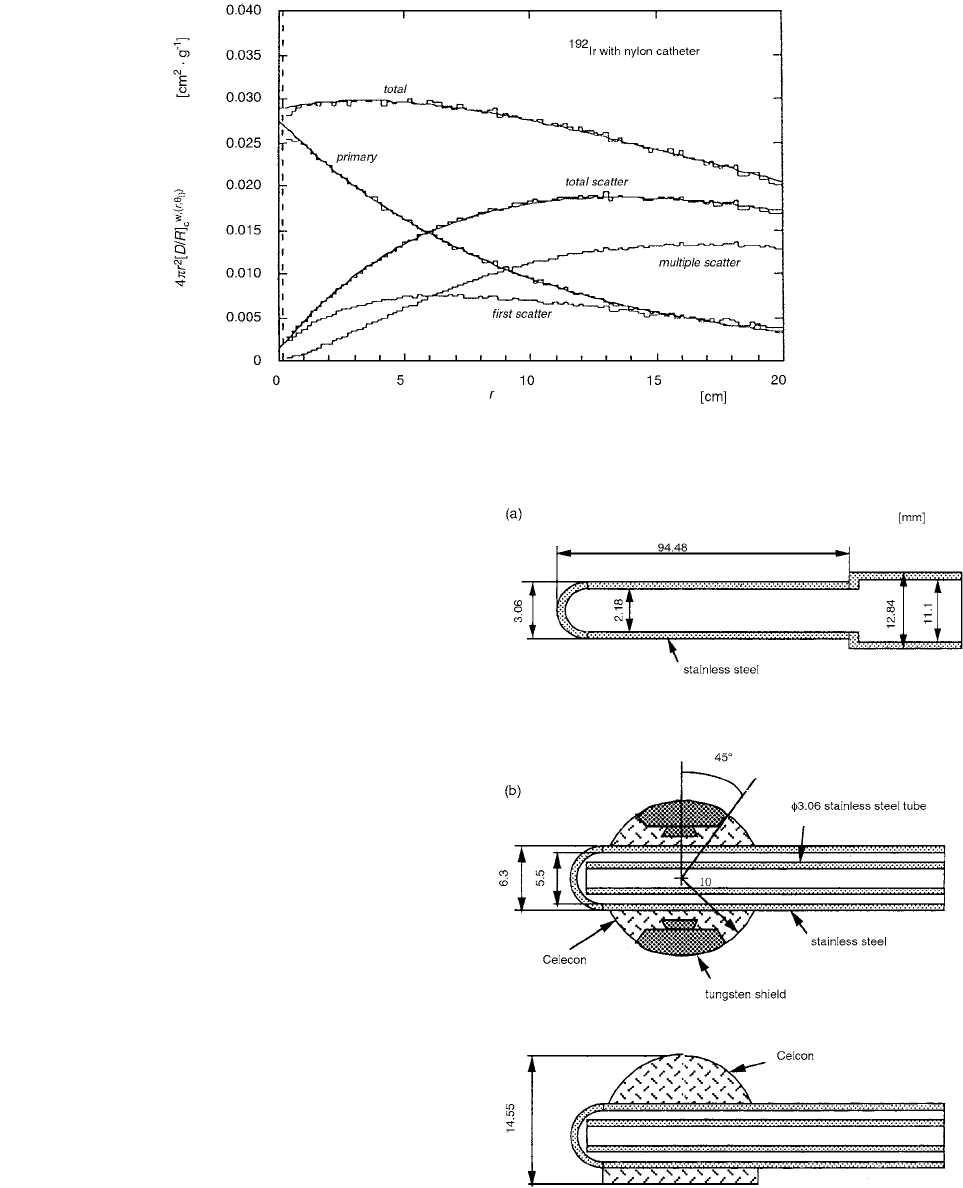
a 0.2-mm wall thickness, is shown in Figure 2.46. The dose
per radiant energy, with the factor removed, and
perpendicular to the bisector of the source out
to a radial distance of 20 cm, is shown for the primary,
first-scatter and multiple-scatter dose fractions separately,
as well as for the total and the all-scatter dose. The all-
scatter dose has a maximum, approximately one photon
mean free path from the source axis, where the build-up
of scattered photons has saturated, and then it decreases as
a function of distance from the source with the overall
attenuation of the primary photon fluence. The parametri-
zations for the total, primary, and scatter doses are also
shown in Figure 2.46 for the primary and scatter doses.
Watanabe et al. [46] have performed computational and
experimental dosimetry of the Henschke applicator with
respect to high-dose rate
192
Ir brachytherapy using a GAM-
MAMED remote afterloader. Monte Carlo simulations
were performed using the MCNP code. The computational
models included the detailed geometry of
192
Ir source, tan-
dem tube, and shielded ovoid. The measured dose rates
were corrected for the dependence of TLD sensitivity on
the distance of measurement points from the source.
Tandem and ovoid schematics are given in Figures
2.47a and 2.47b.
The dose rate at point P at 0.25 cm in water from the
transverse bisector of a straight catheter with an active
pepping source (Nucletron microSelectron HDR source)
with a dwell length of 2 cm was calculated by Wong
et al. [47] using Monte Carlo code MCNP 4-A.
The dose calculation formalism used by the Plato
brachytherapy planning system (BPS) version 13.X is
(2.170)
FIGURE 2.46 Monte Carlo simulation (histogram lines) and parametrization (smooth lines) for
192
Ir source and nylon catheter
combination (from Reference [45] with permission).
4
r
2
()
1
0
2
D
˙
r
,() S
K
en
--------
air
tiss
1
r
2
----
r()F
()
FIGURE 2.47 Longitudinal section of applicators. Dimensions
are in mm. (a) Tandem applicator. (b) Ovoid applicator, planes
through and midway between shield centers. (From Reference
[46]. With permission.)
Ch-02.fm Page 63 Friday, November 10, 2000 10:53 AM
64 Radiation Dosimetry: Instrumentation and Methods
where is the air kerma source strength (Gy m
2
h
1
);
is the ratio of the mean mass energy absorption
coefficient in tissue and air, having a value of 1.11 for the
192
Ir source;
(r) is the modified Van Kleffens and Star
correction for absorption and scattering in water; F(
) is
the anisotropy function; and is the geometric factor.
Equation (2.170) can be modified to the AAPM TG-43
formalism: [47]
(2.171)
where is the dose-rate constant for the source and sur-
rounding medium (cGy h
1
U
1
) (1 U 1 cGy cm
2
h
1
)
for the microSelectron HDR source; the value of in
water is 1.115 cGy h
1
U
1
; g(r) is the radial dose func-
tion; and F(r,
) is the anisotropy factor. In AAPM TG-
43, the recommended value for in water is 1.12, which
is a rounded-off value of 1.115. Strictly, the TG-43 for-
malism uses a line source model for the geometric factor,
but the point source model ( ) is retained here for ease
of comparison [47].
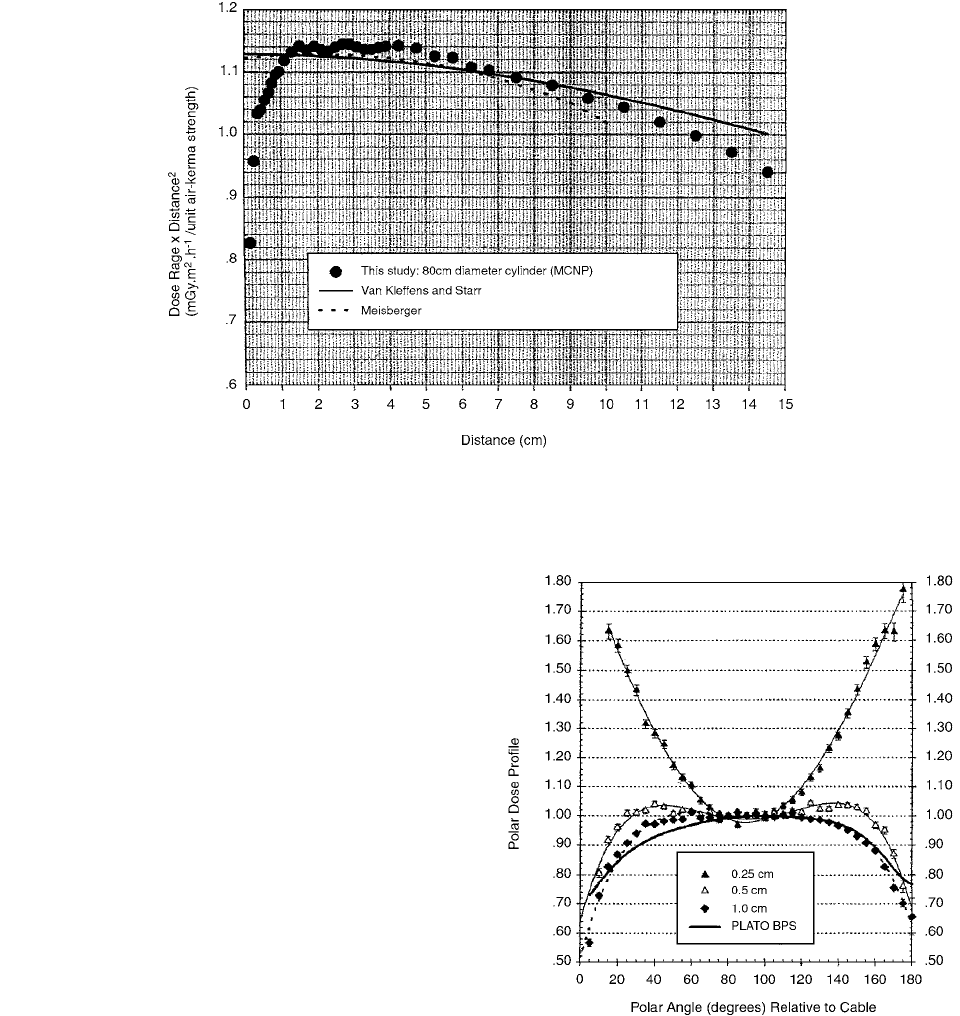
Figure 2.48 shows the variation of the radial dose
(dose rate times distance) with the distance from the
source.
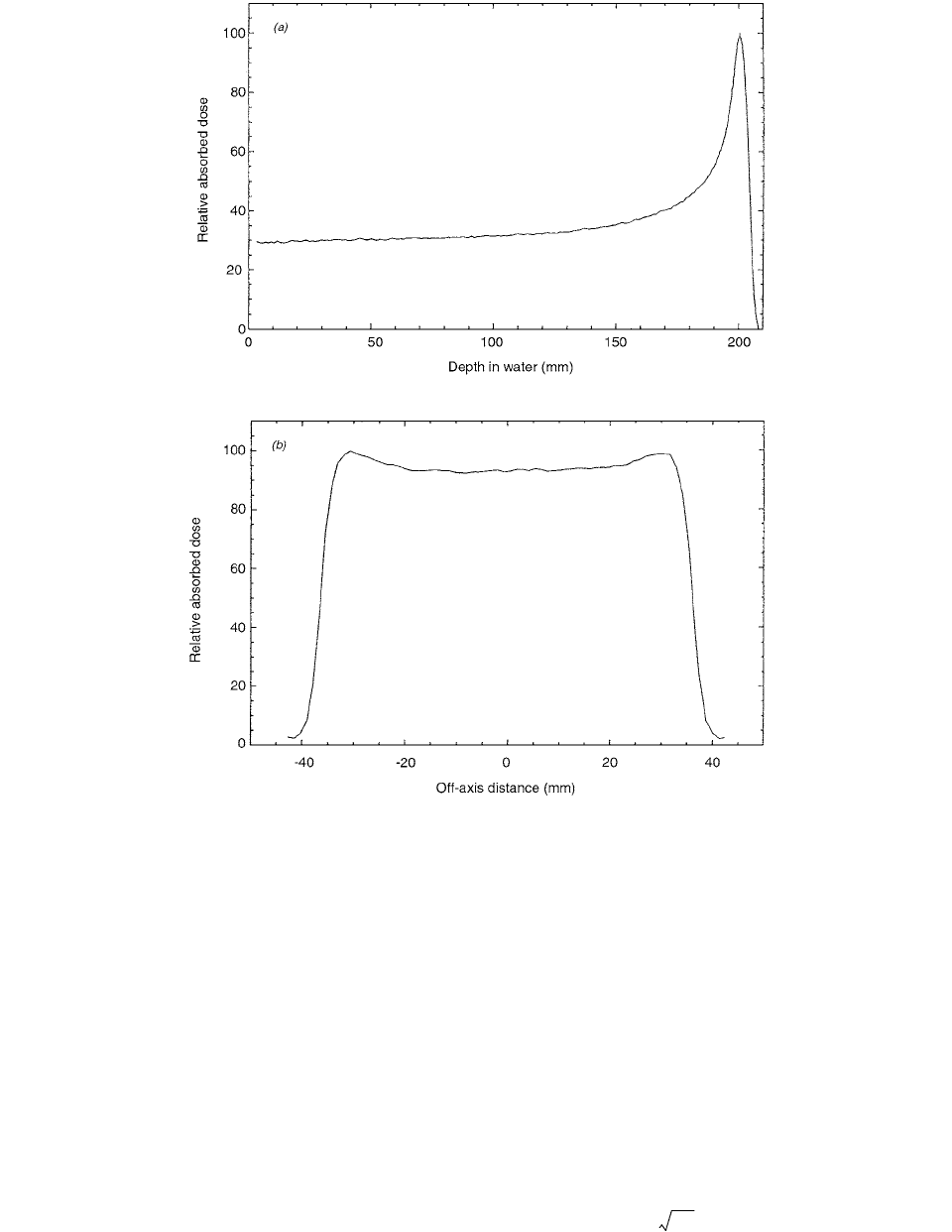
Figure 2.49 shows the angular dose profiles at distances
of 0.25 cm, 0.5 cm, and 1 cm from the source center. The
profiles show significant variation at distances of 0.25 cm
and 0.5 cm from the source center compared with the BPS’s
anisotropy function.
IX. PROTON DOSIMETRY
Protons have a well-defined range in homogenous tissue
and deposit most of their energy at the end of their range
in the so called Bragg peak. Single incident proton beam
FIGURE 2.48 Dose rate times distance
2
(
Gy m
2
h
1
) in a water phantom (80-cm diameter) per unit air-kerma strength (1 U 1
Gr m
2
h
1
) vs. distance from the source center. All results are absolute with no cross-normalization. (From Reference [47]. With
permission.)
S
k
en
()
air
tiss
1r
2
D
˙
r
,() S
k
1
r
2
----
gr()Fr
,()
1r
2
FIGURE 2.49 Monte Carlo calculated polar dose profiles in
water at a distance of 0.25, 0.5, and 1.0 cm from the source
center (normalized to 1.0 at 90
) vs. the polar angle relative to
the source’s cable. The BSP dose profile shows large errors with
the Monte Carlo results at distances of 0.25 and 0.5 cm from
the source center. (From Reference [47]. With permission.)
Ch-02.fm Page 64 Friday, November 10, 2000 10:53 AM
Theoretical Aspects of Radiation Dosimetry 65
can be modulated to produce a flat high-dose region, the
spread-out Bragg peak, at any depth of the body with a
lower dose in entrance region. No dose is deposited past
the distal border of the spread-out Bragg peak. With this
characteristic depth-dose curve, protons have a considerable
potential for sparing normal tissue surrounding a tumor.
Two dosimetry protocols have been published: one by
the American Association of Physicists in Medicine TG
20 [75] and one by the European Clinical Heavy Particle
Dosimetry Group (ECHED) [76], both providing a prac-
tical procedure for the determination of absorbed dose to
tissue or water, in proton beams, using ionization cham-
bers calibrated in terms of air kerma in a
60
Co beam. Both
protocols give an uncertainty of about 4% on this absorbed
dose determination. Because protons undergo little scat-
tering in low-Z materials, it is generally assumed that
perturbations caused by the non-water equivalence of ion-
ization chambers must be very small.
In proton beam dosimetry the use of
N
k
-calibrated
ionization is well established. This is the procedure rec-
ommended by the ECHED dosimetry protocol for thera-
peutic proton beams when no calorimetric calibration of
the ion chamber is available. The American TG-20 protocol
also recommended this procedure as an alternative to cal-
orimetry or Faraday-cup-based dosimetry methods.
A method which reduces the final uncertainity in the
measured dose to water, is to calibrate the ionization
chamber in terms of absorbed dose to water.
Ionization chamber dosimetry of proton beams using
cylindrical and plane-parallel chambers was discussed by
Medin et al. [48]
The formalism in the IAEA Code of Practice for
photon and electron dosimetry [64] can be extended to
proton beams. The absorbed dose to water at the user’s
beam quality, , at the reference point of the ionization
chamber is generally given by
(2.172)
where is the reading of the electrometer plus ioniza-
tion chamber at the user’s beam quality corrected for
influence quantities (temperature, pressure, humidity, sat-
uration, etc.), is the ratio of the mean
energy required to produce an ion pair in the user’s proton
beam quality Q and in the calibration quality , and
is the water to air stopping power ratio in the
user’s beam. The factor contains the product of dif-
ferent perturbation correction factors of the ion chamber
at the user’s beam quality, which generally consists of the
factors , and . These correct, respec-
tively, for the lack of water equivalence of the chamber
wall, the influence of the central electrode of the chamber
both during calibration and in-phantom measurements,
and the perturbation of the fluence of secondary electrons
due to differences in the scattering properties between the
air cavity and water. If the concept of effective point of
measurement is not used and the determination of
absorbed dose is referred to the center of the ionization
chamber, a fourth factor has to be included in
to take into account the replacement of water by the
detector. is the absorbed dose to air chamber factor
at the beam quality used by the dosimetry laboratory,
which is defined by the well-known relation. [64]
(2.173)
In the formalism the absorbed dose to water at the
center of the chamber is given by the relationship
(2.174)
where is obtained at the standard laboratory from
the knowledge of the absorbed dose to water at the point
of measurement in water for the calibration quality,
(2.175)
The factor in Equation (2.174) corrects for the
difference in beam quality at the standard laboratory and
at the user’s facility and should ideally be determined
experimentally at the same quality as the user’s beam.
When no experimental data are available, can be
calculated according to the expression
(2.176)
It should be noted that the chamber-dependent correction
factors and are not included in the definition of .
Another potential advantage in the use of a calibration
factor in terms of absorbed dose to water is that the product
of and , referred to as
, can be determined
using calorimetry with a much higher accuracy than that
obtained when the two factors are considered indepen-
dently, yielding
(2.177)
The expression for of a plane-parallel ionization
chamber can be written as
(2.178)
N
D
D
wQ,
P
eff
D
wQ,
P
eff
() M
Q
N
DQ
0
,
W
air
()
Q
0
W
air
()
Q
0
[]S
w air,
()
Q
p
Q
M
Q
W
air
()
Q
W
air
()
Q
0
Q
0
s
wair,
()
Q
p
Q
p
wall
p
cel gbl
,
P
ca
v
P
displ
P
Q
N
DQ
0
,
N
DQ
0
,
N
KQ
0
,
1 g()k
air
k
m
N
w
D
wQ,
M
Q
N
wQ
0
,
k
Q
N
wQ
0
,
N
wQ
0
,
D
wQ
0
,
M
Q
0
k
Q
k
Q
k
Q
s
wair,
()
Q
s
wair,
()
Q
0
[]W
air
()
Q
0
W
air
()
Q
0
[]P
Q
P
Q
0
()
k
att
k
m
k
Q
s
wair,
W
air
k
Q
w
Q
w
Q
0
()p
Q
p
Q
0
()
N
D
N
Dx,
N
D ref,
M
ref
p
cav,ref
p
cel-gbl ref,
M
x
p
cav,x
p
wall,x
p
cel-glb x,
Ch-02.fm Page 65 Friday, November 10, 2000 10:53 AM
66 Radiation Dosimetry: Instrumentation and Methods
where the numerator corresponds to the determination
using the reference chamber (usually cylindrical) and
stopping power ratios cancel out. and are the
average ratios of the readings of the two chambers to those
of an external monitor to take into account possible accel-
erator output fluctuations.
Figure 2.50 shows the 170-MeV unmodulated proton
depth-ionization distribution, measured with a silicon diode
detector (Figure 2.50a), together with a transverse scan of
the proton field at the depth where the ion chamber mea-
surements were performed. It should be pointed out that
the increase in dose at the lateral edges of the field (shown
in Figure 2.50b) arises from protons scattered in the colli-
mator and is not related to the design of the flattening filters.
Proton pencil beams in water, in a format suitable for
treatment-planning algorithms and covering the radiother-
apy energy range (50–250 MeV), have been calculated by
Carlsson et al. [49] using a modified version of the Monte
Carlo code PTRAN.
A general assumption in the straggling theories of
heavy charged particles is that the distribution of ranges
is described by a Gaussian function
(
); this is justified
for heavy charged panicles, since hard collisions are rare
and bremsstrahlung generation is negligible. The distribu-
tion of the ranges is described by
(2.179)
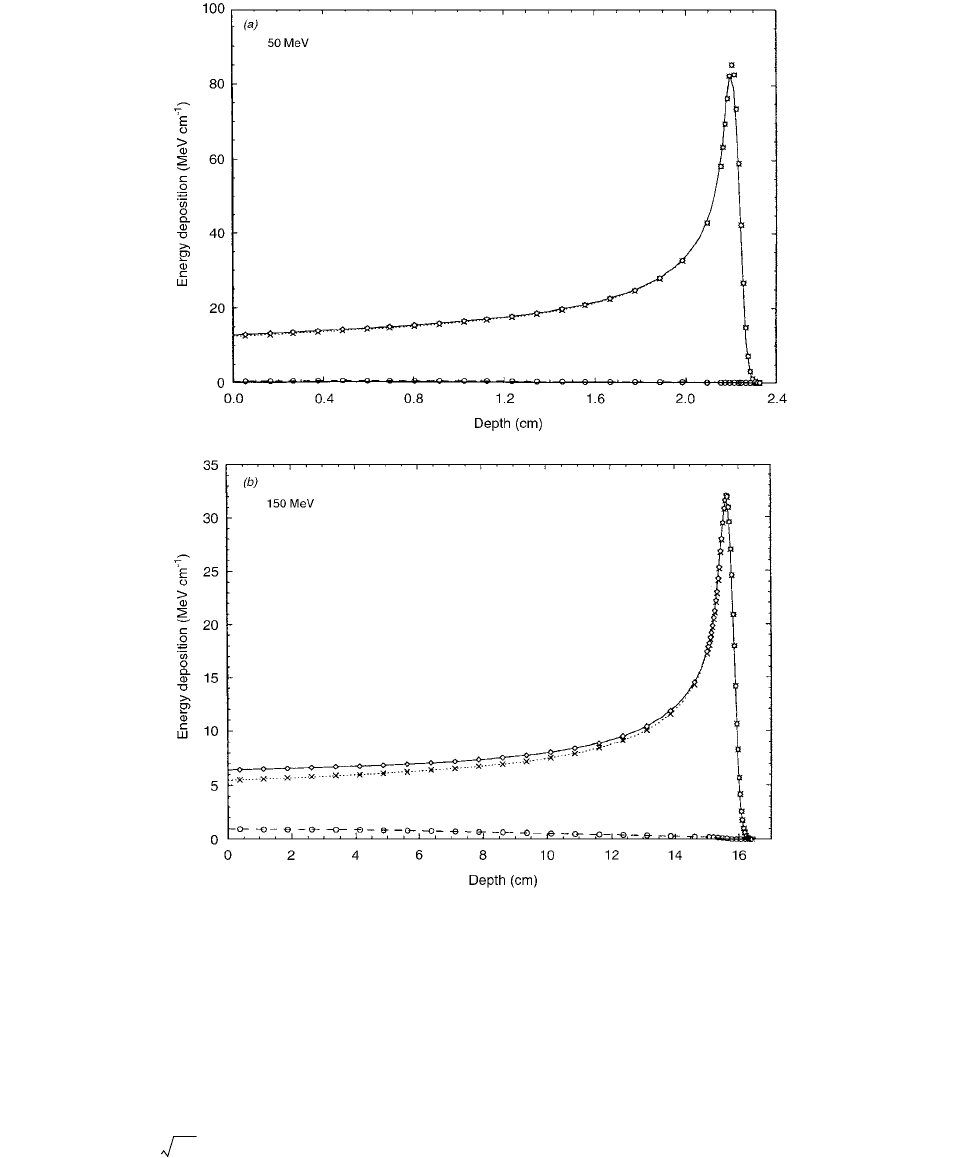
The broad-beam central-axis depth-dose distribution,
D(z), is then calculated by convolving the specific energy
FIGURE 2.50 (a) The central axis depth-ionization distribution of the 170-MeV unmodulated proton beam used in this investigation,
measured with a silicon diode detector. (b) A transverse scan of the proton field at the depth of 29 mm where the measurements with
the ionization chambers were performed. (From Reference [48]. With permission.)
D
w
M
ref
M
x
()
1
2
z()
-----------------------
e
r
0
()
2
2
2
z()
----------------------------
Ch-02.fm Page 66 Friday, November 10, 2000 10:53 AM
Theoretical Aspects of Radiation Dosimetry 67
deposition distribution, d(z), in the csda with the range
straggling distribution,
(
), according to
(2.180)
where d(
z) is the specific energy deposition at the
distance (
z) from the end of the depth-dose curve,
(z) is the standard deviation in position of the protons at
the depth z, and is the csda range. Broad-beam central
axis depth-dose distribution for 50 and 150 MeV protons
is shown in Figure 2.51.
Proton depth-dose distribution was discussed by
Palmans and Verhaegen. [50] The extended use of proton
beams in clinical radiotherapy has increased the need to
investigate the accuracy of dosimetry for this type of
beam. As for photon and electron beams, Monte Carlo
simulations are a useful tool in the study of proton dosim-
etry. The existing proton Monte Carlo code PTRAN, devel-
oped for dosimetry purposes, is designed for transport of
protons in homogeneous water only. In clinical proton
dosimetry, as well as in treatment conditions, several other
materials can be present, such as plastic phantoms, plastic
modulator wheels, and several materials in ionization
FIGURE 2.51 Broad-beam central-axis depth-dose distributions for 50-, 150-, and 250-MeV protons from PTRAN and Carlsson
et al. analytical model. The total depth-dose distribution (solid line, PTRAN,
, analytical) as well as the individual contributions
from Colomb (short dashes, PATRAN;
, analytical) and inelastic nuclear interactions (long dashes, FTRAN; O, analytical) are
shown. (From Reference [49]. With permission.)
Dz()
z()d
2
z()
-----------------------
e
r
0
()
2
2
2
z()
----------------------------
d
r
0
Ch-02.fm Page 67 Friday, November 10, 2000 10:53 AM
68 Radiation Dosimetry: Instrumentation and Methods
chambers. Investigation of protons transport in other
media started from the PTRAN code and implemented
proton transport in other materials, including heteroge-
neous systems composed of different materials. With this
extended code, calculations of depth-dose distributions
for some low-Z materials are performed and compared
with those obtained for water. The results show that for
plastics (PMMA, polystyrene, and A-150), the depth-
dose characteristics are comparable to those of water.
For graphite, air, and aluminum, larger differences are
observed.
The original code PTRAN, developed and described
extensively by Berger [52], simulates monodirectional
monoenergetic proton beams in homogeneous water with-
out transport of secondary particles. The depth doses
obtained from the calculations agreed well with those for
three experimental proton beams with energies above 150
MeV. The Bragg peak was characterized by a number of
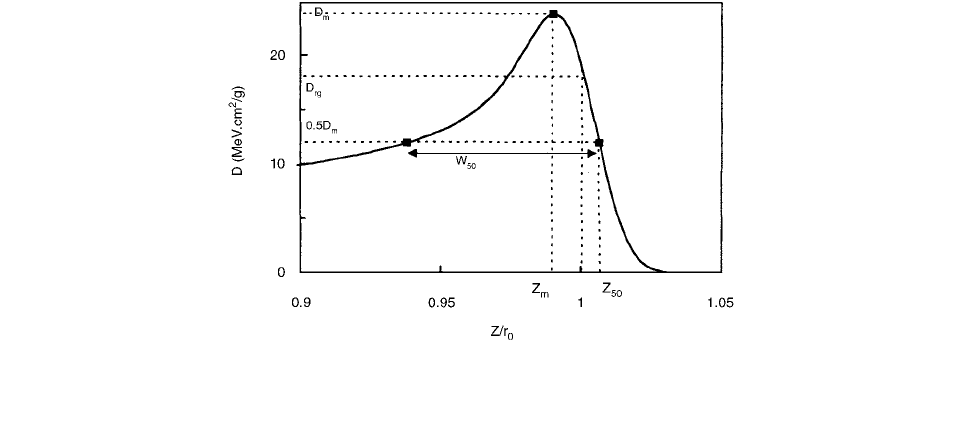
parameters of which a limited number, used in our study,
are shown in Figure 2.52. These parameters are the depth
at which the maximum dose occurs; , the dose
at the CSDA range (taken from ICRU report 49 [78];
, the peak width at 50% of the maximum dose; and ,
the depth distal to the Bragg peak where the dose amounts to
50% of the maximum dose. All depths and widths are
expressed relative to . The entrance dose was also
calculated. In Berger [52] it is shown that the radial dose
distributions obtained with PTRAN agree with theoreti-
cal calculations based on Molliere’s theory. Palmans and
Verhaegen’s calculations show that the root mean square
(rms) values of the radial-dose distributions also agree
with those obtained with the Fermi-Eyges method except
at the end of the range, where the Fermi-Eyges method
gives a steeper decrease. This is because the latter method
does not include energy loss straggling.
An analytical approximation of the Bragg curve for
therapeutic proton beam was discussed by Bortfeld. [53]
The model is valid for proton energies between about 10
and 200 MeV. Its main four constituents are:
1. a power-law relationship describing the range-
energy dependency;
2. a linear model for the fluence reduction due to
nonelastic nuclear interactions, assuming local
deposition of a fraction of the released energy;
3. a Gaussian approximation of the range-strag-
gling distribution; and
4. a representation of the energy spectrum of poly-
energetic beams by a Gaussian with a linear “tail.”
Based on these assumptions, the Bragg curve can be
described in closed form using a simple combination of
Gaussians and parabolic cylinder functions.
Consider an initially monoenergetic broad proton
beam along the
z axis, impinging on a homogeneous
medium at z 0. The energy fluence, , at depth z in the
medium can be written in the form:
(2.181)
where (z) is the particle fluence, i.e., the number of
protons per cm
2
, and E(z) is the remaining energy at depth
z. The total energy released in the medium per unit mass
(the “terma,” T) at depth z is then:
(2.182)
where
is the mass density of the medium. The first term
in the brackets represents the reduction of energy of the
FIGURE 2.52 Parameters , and , defined in the text, used by Berger [51] and by Palmans and Verhaegen [50]
to characterize the Bragg peak of the depth-dose distribution (numerical values are for 200-MeV monoenergetic protons). (From
Reference [50]. With permission.)
z
m
z
50
w
50
D
m
,, , D
rg
z
m
D
m
D
rg
r
0
w
50
z
50
r
0
D
0
z() z()Ez()
Tz()
1
---
d
dz
--------
1
---
z()
dE z()
dz
--------------
d z()
dz
---------------
Ez()
Ch-02.fm Page 68 Friday, November 10, 2000 10:53 AM

Theoretical Aspects of Radiation Dosimetry 69
protons during their passage through matter. The “lost”
energy is transferred mainly to atomic electrons. The range
of these secondary electrons is negligible for our purposes.
This is due to the fact that only a relatively small energy is
transferred to each electron, which, in turn, is due to the
small ratio of electron and proton mass. Therefore, the
terma corresponding with the first term of Equation (2.182)
produces an absorbed dose which is equal to the terma.
The total absorbed dose, , is consequently given by
(2.183)
In order to determine this depth-dose curve, only the func-
tional relations
E(z) and (z) are needed. These are
obtained from the known range-energy relationship
and the probability of nonelastic nuclear interactions,
respectively.
The relationship between the initial energy E
and the range in the medium is given approx-
imately by
(2.184)
With p 1.5, this relationship is known as Geiger’s
rule, which is valid for protons with energies up to about
10 MeV. For energies between 10 and 250 MeV, the expo-
nent p increases to . The factor
is approximately
proportional to the square root of the effective atomic mass
of the absorbing medium, (Bragg-Kleeman rule).
It is also inversely proportional to the mass density of the
medium (see Figure 2.53).
The depth-dose distribution is calculated by [53]
(2.185)
which is of the form
(2.186)
The first term, , is the dose contribution from
those protons that have no nuclear interactions. It is pro-
portional to the (non-nuclear) stopping power and exhibits
to some degree the form of a Bragg curve, as it increases
monotonically from z 0 to and has a peak at
. However, due to the neglect of range straggling, the
peak is unrealistically sharp and there is a singularity at
. The second term, , represents the dose
delivered by the relatively small fraction of protons that
have nuclear interactions. It decreases monotonically and
is zero at . Note that comprises the dose
resulting not only from nuclear but also non-nuclear
interactions that take place before the nuclear collision.
FIGURE 2.53 Range-energy relationship according to ICRU 49 and analytical fit with Equation (2.184). The error bars represent a
relative error of the ICRU data of
1.5%. (From Reference [53]. With permission.)
D
ˆ
z()
D
ˆ
z()
1
---
z()
dE z()
dz
--------------
d z()
dz
---------------
Ez()
z 0()
E
0
zR
0
R
0
E
0
p
p 1.8
A
eff
D
ˆ
z()
0
R
0
z()
1 p()1
p()R
0
z()
1 p/
p
1 p/
1
R
0
()
-----------------------------------------------------------------------------------------------------
for zR
0
for zR
0
0
D
ˆ
z() D
ˆ
1
z() D
ˆ
2
z()
a
1
R
0
z()
1/p 1
a
2
R
0
z()
1 p/
D
ˆ
1
z()
zR
0
R
0
zR
0
D
ˆ
1
z()
zR
0
D
ˆ
1
z()
Ch-02.fm Page 69 Friday, November 10, 2000 10:53 AM
