Seuront L. Fractals and Multifractals in Ecology and Aquatic Science

Подождите немного. Документ загружается.

64 Fractals and Multifractals in Ecology and Aquatic Science

the positive kurtosis shows a distribution that is more peaked than expected in the case of normal-

ity (g

= 1.83). As organisms foraging for food (for example, the amphipod C. arenarium; see

Section 3.2.3) are likely to actively select areas of high chlorophyll a concentration, they may take

advantage of positively skewed distribution. Equation (3.22) was then applied to the distribution pat-

tern of chlorophyll a concentration higher than a given threshold (such as C > 8.85 mg Chl.a m

–2

;

Figure 3.20B) to investigate the relative advantages that foraging organisms may have to actively select

a specic range of food concentrations. The whole plot has size 15 × 15 in plot units, and each pixel

represents a surface of 6.67 × 6.67 cm in the eld. The log-log plot of m(d) vs. d exhibits a very clear

scaling behavior, resulting in the mass dimension D

= 1.82 for C > 8.85 mg Chl.a m

−2

(Figure 3.20C).

More generally, the fractal dimensions D

related to chlorophyll a concentrations ranging from 1.9 to

26.6 mg Chl.a m

−2

clearly decrease with increasing chlorophyll a concentration (Figure 3.21).

3.2.4.2.4 Ecological Interpretation

Low chlorophyll densities (C ≤ 6.65 mg Chl.a m

−2

) are characterized by high fractal dimensions,

= 1.89 ± 0.01. Such high dimensions (the maximum value that D

can reach is D

= 2.00) char-

acterize very complex processes where short-range, local variability is highly developed and tends to

obfuscate long-range trends; the variable is more evenly or regularly distributed (that is, less struc-

tured) in space. In other words, this indicates that the variation within a sampling unit is equal to

the variation among the sampling units. Alternatively, the dimensions D

related to high chlorophyll

concentrations (C ≤ 6.65 mg Chl.a m

−2

) are very low (D

= 1.03 ± 0.02) and cannot be distinguished

from the lower D

value (D

= 1). This indicates that the variability of high microphytobenthos

concentrations is characterized by the so-called random point pattern (Li 2000) (see Figure 2.9D).

Finally, patches corresponding to intermediate chlorophyll a concentrations (7.60 ≤ C ≤ 21.85 mg

Chl.a m

−2

) are characterized by decreasing fractal dimensions D

from D

= 1.85 to 1.07. According

to the optimal foraging theory (Pyke 1984), organisms are expected to optimize the energy required

to capture a given amount of food. This is particularly relevant here as food availability changes

depending on its fractal dimension. A low fractal dimension relates to a smooth and predictable dis-

tribution of food items gathered in a small number of patches. In contrast, a high fractal dimension

means rough, fragmented, space-lling and less predictable distribution. When a predator has no

2.0

Mass Dimension D

1.8

1.6

1.4

1.2

1.0

3.8 7.6 11.4 15.2 19.0

22.8 26.6

Figure 3.21 Mass fractal dimension D

estimated from discrete patterns of increasing microphytobenthos

chlorophyll a concentrations. The dimension D

is estimated as the slope of the log-log plot of m(d ) vs. d

(Equation 3.20). (See Figure 3.20C.)

2782.indb 64 9/11/09 12:04:55 PM

Self-Similar Fractals 65

detection ability, prey distributions with high dimensions should be more efcient, as food avail-

ability (which is here equivalent to the predator–prey encounter rates) becomes proportional to the

searched volume as fractal dimension increases. When a predator can remotely detect food items,

prey distributions with low fractal dimension should be relatively better. Given the sensory abilities

of intertidal organisms preying on microphytobenthos (see, for example, Erlandson and Kostylev

1995; Hutchinson et al. 2007), in the specic case studied here, microphytobenthos grazers should

then derive maximum benet from high concentration patches.

3.2.4.3 comparing the mass dimension D

to other Fractal dimensions

From Equations (3.9) and (3.10), and from Equations (3.19) and (3.20), it is readily seen that for

strictly self-similar mathematical fractals, such as the Cantor dust (Figure 3.3) and the Sierpinski

carpet and gasket (Figure 2.8), the mass dimension D

is the same as the Hausdorff dimension D

and strictly speaking to any other fractal dimension related to Equations (3.9) and (3.10) in this

section. However, for real-world fractals, there are signicant differences. The mass dimension can

nevertheless still be directly compared to the box dimension, D

Consider the mass of occupied pixels in a window (that is, box) of size (d ) as:

()

(3.23)

where

()

is the mass of the occupied pixels

()

, and

()

the total number of pixels in the

ith box of size d. The average mass,

m()

, in

N()

boxes of size d is then:

()

∑

(3.24)

Now, rethinking Equation (3.23) in terms of probabilistic arguments leads to expressing count fre-

quencies as probability density function p(d) following:

() ()

δδ

∑

(3.25)

One may note here that for a given value of d, the mass m(d ) is expressed as the rst moment (that

is, the mean) of the probability distribution as:

mNp

() ()

δδδ

()=

∑

(3.26)

Using Equations (3.25) and (3.24) can be equivalently thought of as

mN() /(),

δδ

leading to

rewrite Equation (3.22) as:

()

δδ

−

(3.27)

which is fully similar to the power-law relationship used to estimate the box dimension (

()

δδ

−

leading to:

(3.28)

2782.indb 65 9/11/09 12:05:03 PM

66 Fractals and Multifractals in Ecology and Aquatic Science

and using Equation (3.17) to

= D

(3.29)

The mass and box dimensions estimated for the distribution pattern of Corophium arenarium

shown in Figure 3.17A are respectively D

= 1.29 ± 0.02 and D

= 1.28 ± 0.01, and cannot statisti-

cally be distinguished (p > 0.05) from the cluster dimension estimated in Section 3.2.3.2, D

= 1.28 ±

0.02. Similarly, the mass, box, and cluster dimensions estimated from the microscale distribution

patterns of microphytobenthos chlorophyll biomass (Figure 3.20A) cannot be statistically distin-

guished whatever the chlorophyll a concentration C considered.

3.2.5 in F o r m a T i o n di m E n s i o n , D

3.2.5.1 theory

The information dimension, D

, can be conceptually related to the box dimension D

and

the cluster dimension D

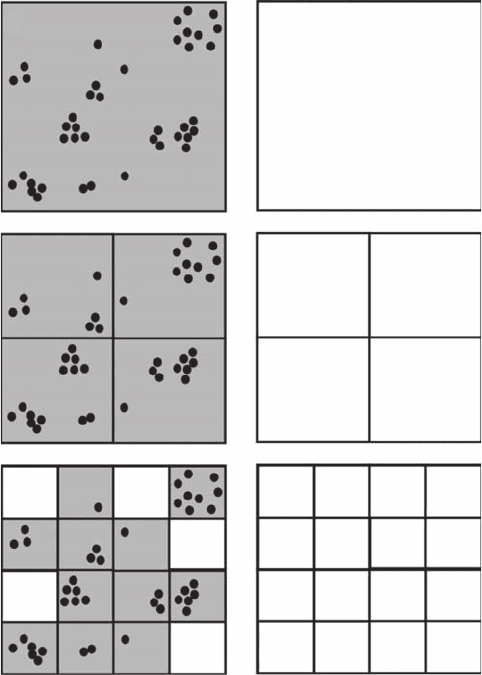
, because it is based on a count of occupied boxes of varying size d

(Figure 3.22). However, in the box and the cluster dimension estimates, a box is counted as occu-

pied (Figure 3.22A,B,C) and enters the calculations of N(d) (see Equations 3.12 and 3.14), regardless

1014

621

Figure 3.22 Schematic illustration of three successive steps of the box-dimension procedure, or equiva-

lently the cluster dimension procedure (A, B, C) and information dimension procedure (D, E, F) using three

different characteristic box sizes: d

(A, D), d

(B, E), and d

(C, F) dened as d

= 2d

= 4d

2782.indb 66 9/11/09 12:05:05 PM

Self-Similar Fractals 67

of whether it contains one point or a relatively large number of points. The information dimen-

sion provides more details, as the number of points n

within each occupied box are counted

(Figure 3.22D,E,F), and is expressed as the relative frequency f

(3.30)

where

is the total number of points in the set

()

, and

N()

is the number of occupied

boxes of size d. A weight is then assigned to each box; the boxes containing a greater number of

points count more than boxes with fewer points. The information entropy, or Shannon entropy

H()

at a scale d is subsequently dened as:

Hff

() log

()

=−

∑

(3.31)

Consider now a uniformly distributed point pattern in one-, two-, and three-dimensional spaces.

The number of points

and the frequencies

are thus proportional to

−1

−2

, and

−3

and to

, and

, respectively. Equations (3.12) and (3.14) are subsequently rewritten as;

HkD

() loglog

δδ

=−

(3.32)

where

is a constant. For nonuniformly distributed point patterns, the information dimension

is subsequently dened as:

HkD

() loglog

δδ

=−

(3.33)

where

is still a constant.

3.2.5.2 comparing the information dimension D

to other Fractal dimensions

Although the above-mentioned arguments lead us to consider the information dimension as a gen-

eralization of the box dimension, these dimensions are nevertheless not equal. Consider a uni-

form point pattern embedded in a

-dimensional space. All the frequencies

are equal, each

=1/ ()

and Equation (3.31) leads to

HN() log()

δδ

, that is, the maximum value of

H()

. All

the other (that is, smaller) values of

H()

thus quantify the nonuniformity of the point pattern or

alternatively correct the dimension estimate by giving less weight to the boxes that contain relatively

fewer points. In other words, if one denes the information dimension as:

→

lim

()

log( /)

(3.34)

and goes back to the formulation of the box dimension (Equation 3.15), it comes that:

(3.35)

for uniform point patterns, and

(3.36)

for nonuniform point patterns. The validity of Equations (3.33) and (3.34) is illustrated by the infor-

mation dimension analysis of the microscale distribution of the amphipod Corophium arenarium

2782.indb 67 9/11/09 12:05:21 PM

68 Fractals and Multifractals in Ecology and Aquatic Science

(Section 3.2.3; Figure 3.17A) and the related simulated uniform point pattern (Section 3.2.3)

(Figure 3.17B). As predicted by Equation (3.35), the information and box dimensions of the uni-

form point pattern cannot be statistically distinguished (p > 0.05). In turn, the information dimen-

sion D

is signicantly different from the box dimension D

for the point pattern of C. arenarium

(p < 0.01). Farmer et al. (1983) rened the denitions of both box and information dimensions,

stating that D

is a “metric dimension” (that is, it depends only on metric scaling properties, d),

while

is a “probabilistic dimension” (that is, it depends on both metric, d, and probabilistic,

properties).

3.2.6 co r r E l a T i o n di m E n s i o n , D

c o r

3.2.6.1 theory

The correlation dimension is well adapted to the characterization of spatial clustering in point pat-

terns and was initially introduced to characterize the dimension of strange attractors (see Section

6.1.3). This method, widely used in empirical analyses of dynamical systems (Grassberger and

Procaccia 1983) and in cosmology (McCauley 2001), has, to our knowledge, never been used in

ecology. A generalization of this method to the stochastic process has been applied by Ibanez (1986)

and Seuront (1999, 2004) to plankton transects and time series, respectively (see Chapter 6). The

correlation function of a point pattern, usually referred to as the correlation integral

C()δ

, is calcu-

lated as (Hentschel and Procaccia 1983):

() ()

δδ

∑

(3.37)

where

() ()

δθδ

=−

≠=

is the number of distinct pairs of points in a circle (or equivalently

a sphere if the point pattern is embedded in three dimensions) of radius

centered on the ith of

N points,

ij,

is the Euclidean distance between the ith and the jth points (

dxx

ij ij,

||=−

), and q(x)

is the Heaviside function, dened as

()x = 0

and

()x = 1

for

x < 0

and

x ≥ 0

, respectively. It is

possible to take 0 < d < 1. This means that the original dimensional variable d for each point has

been rescaled by dividing it by d

max,i

, where d

max,i

is the value of the unscaled variable d for which

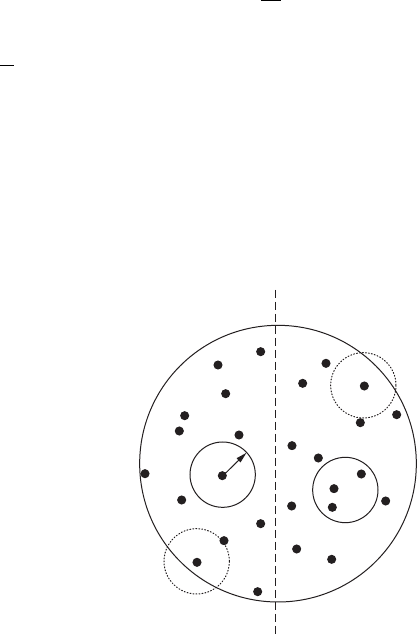
the radius d, centered on point i, just touches the boundary of the data set (Figure 3.23).

Figure 3.23 A point pattern, illustrating which clusters are used (solid circles) and not used (dashed circles)

in the search for scale invariance.

2782.indb 68 9/11/09 12:05:30 PM

Self-Similar Fractals 69

Equation (3.37) can be rewritten more simply as:

()

(3.38)

where

is the total number of pairs of points in the set, and

ij,

is the number of pairs with

ij,

In other words, the correlation integral

C()

represents the probability that the distance

between a pair of randomly chosen points will be less than a distance d

apart. In the case of a uni-

form point pattern, the correlation integral scales with the distance d

as:

C(d ) = kd

(3.39)

while for nonuniform distributions, C(d) is given by:

C(d ) = kd

cor

(3.40)

where

is a constant and the exponent

cor

is the correlation dimension, estimated as the slope of

the log-log plot of C(d ) vs. r.

3.2.6.2 comparing the correlation dimension D

cor

to other Fractal dimensions

Considering the correlation dimension as:

cor

→

lim

log()

log( )

(3.41)

leads to:

DDD

corib

(3.42)

for uniform point patterns, and it is seen from the comparison of Equations (3.13), (3.32), and (3.39) that:

DDD

corib

(3.43)

for nonuniform distributions. The correlation dimension D

cor

, information dimension D

, and box

dimension D

returned by respectively applying Equations (3.36), (3.29), and (3.12) to the microscale

point pattern of the amphipod Corophium arenarium (see Section 3.2.3, Figure 3.17A) and the

related uniform point pattern simulated with the same number of data points (see Section 3.2.3,

Figure 3.17B). As predicted by Equation (3.42), the correlation, information, and box dimensions of

the uniform point pattern are not statistically different ( p > 0.05) (Figure 3.24). On the other hand,

the three dimensions D

cor

, D

, and D

are signicantly different (p < 0.05) for the point pattern

of C. arenarium, with D

cor

= 1.15 ± 0.01, D

cor

= 1.22 ± 0.02, and D

cor

= 1.28 ± 0.02 (Figure 3.24),

hence verifying Equation (3.43). Chapter 5 shows in detail how the correlation dimension D

cor

, the

information dimension D

, and the box dimension D

can also be related using a generalization of

the entropy formulation introduced in Equation (3.31).

3.2.7 ar E a -pE r i m E T E r di m E n s i o n s

Area-perimeter methods have generally been used to estimate the fractal dimension of objects

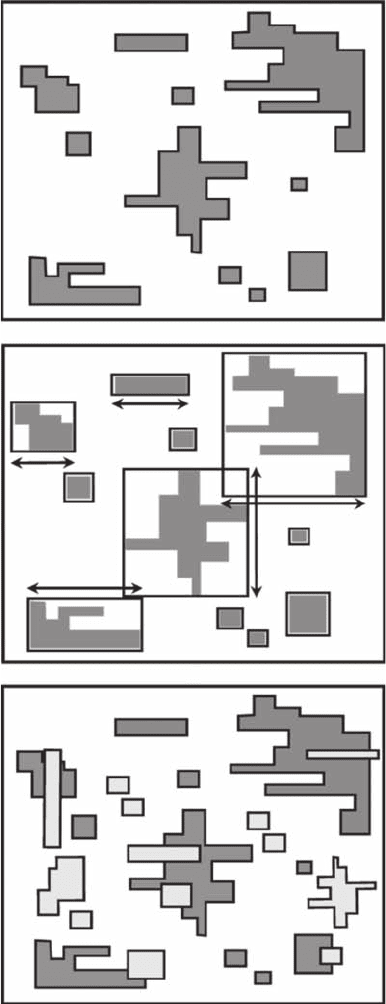
coded as digitized images. Consider as an example a landscape consisting of a set of vegetation

patches (Figure 3.25). These patches can be either monospecic (Figure 3.25A,B) or plurispecic

(Figure 3.25C). Area-perimeter dimension methods can be used to determine the fractal dimen-

sion of a set of patches as a function of the complexity of their boundaries or their space-lling

2782.indb 69 9/11/09 12:05:36 PM

70 Fractals and Multifractals in Ecology and Aquatic Science

character and also as a function of the quality of the surrounding patches. Three approaches are

thus possible:

Perimeter-based• , to determine the extent that a patch perimeter lls the plane

Area-based• , to determine the extent that a patch lls the plane

Landscape-based• , to compare patch complexity in an environment characterized by

patches of different types

Each of the three methods described in this section measures a fractal dimension, but it will be

shown that their application and interpretation are quite different.

3.2.7.1 Perimeter dimension, D

The perimeter dimension (D

) method basically provides a measure of the perimeter-area ratio for

a patch or a set of patches (Figure 3.25A). Consider an “ideal” circular patch (for example, Okubo 1980)

in a two-dimensional space. The area A and the perimeter P are related as:

PrrA A

== ≈

==≈

ππ

(3.44)

where r is the radius of the patch, and “

≈

” means proportionality. In case of a non-Euclidean patch

structure, Equation (3.44) leads to the following perimeter-area relationship:

PkA

(3.45)

where k is a constant, the area A is the number of pixels needed to cover a given object, the perimeter

P is the number of pixel edges, and D

is the perimeter dimension. For a single patch, the perimeter

dimension is thus simply written as:

DPA

= 2log /log

(3.46)

2.0

1.8

1.6

Fractal Dimension

1.4

1.2

1.0

corr

Figure 3.24 Correlation dimension D

cor

, information dimension D

, and box dimension D

estimated for the

microscale point pattern of the amphipod Corophium arenarium (see Figure 3.16) and a simulated uniform

point pattern with the same number of data points.

2782.indb 70 9/11/09 12:05:40 PM

Self-Similar Fractals 71

Figure 3.25 Area-perimeter dimensions. (A) Perimeter dimension D

is based on estimates of patch areas

(light gray) and perimeter (indicated by a black solid line). (B) Area dimension D

is based on estimates

of patch areas and largest horizontal or vertical dimension (n). (C) Landscape/seascape dimension D

a generalization of the perimeter dimension to patches of different species, here shown by different gray

intensities.

2782.indb 71 9/11/09 12:05:42 PM

72 Fractals and Multifractals in Ecology and Aquatic Science

Alternatively, the slope of the log-log area-perimeter plot for a set of objects gives a fractal dimen-

sion (Burrough 1986). Patterns characterized by perfectly circular patches (that is, a low perimeter-

area ratio) have a fractal dimension

, while those containing highly convoluted patches (that

is, a high perimeter-area ratio) have a fractal dimension

→2

. This method is thus well adapted

to studies focusing on ecotonal boundaries (edges).

However, a digitized image of any fractal object is Euclidean by virtue of its projection onto a

grid, and thus leads to biased estimates of

; see, for example, Falconer (1993), and Section 7.2.1.

As a remedial procedure, the expression of the perimeter P in Equation (3.45) needs to be modied

as (Olsen et al. 1993):

PPA

21=+−[()]

(3.47)

The ratio 1:4 is determined as the proportionality constant for pixelized systems, and

21()A−

the maximum value of the perimeter fractal dimension

of an object of area

considered on

a square grid. The corrected perimeter

should then be used instead of

when estimating

from Equation (3.45). Some additional limitations related to the representation of digital images are

discussed in Section 7.2.1.

3.2.7.2 area dimension, D

To quantify the space-lling characteristics of a patch (Figure 3.25B), Voss (1988) modied the stan-

dard box-counting framework (see Section 3.2.2) and suggested that the fractal dimension of a patch

can be instead measured as D

= log A/log L, where L is the maximum of the row and column lengths

of the pixelized patch. Square patches of size n

(Ln=

An=

) completely ll a two-dimensional

space (that is,

Dnn

2==log/log

), while for a “rectangular” patch of length

and width 1

(

Ln=

An=

Dnn

==log/log1

. The corresponding length-area relationship is written as:

A = kL

(3.48)

where k is a constant, and

the area dimension. This method returns high fractal dimensions for

patches that best ll their embedding space (that is, circular patches). Thus, in studies focusing on

acquisition and retention of space—for instance, in the framework of invading species (Kooi and

Kooijman 2000)—a circular patch (where the area-to-edge ratio is high) would be more likely to

retain space than a thin, convoluted patch (that is, where the area-to-edge ratio is low).

3.2.7.3 landscape/seascape dimension, D

This framework is a generalization of the perimeter-area relationship provided above to a set of

patches of different types (for example, patches of different seagrass species; Figure 3.25C) to esti-

mate the extent to which the perimeter of a given patch interacts with neighboring patch types.

The related measure of fractal dimension, the so-called landscape/seascape dimension D

, can be

estimated using a modied perimeter length P

(Olsen et al. 1993):

= P + [2(A − 1)(N/(N − 1))]

(3.49)

where P and A are respectively the patch perimeter and area, N is the number of adjacent patch

types, and N

is the number of all patch types in the landscape/seascape. The related fractal dimen-

sion for the seascape is subsequently estimated by substituting Equation (3.48) into the perimeter-

area relationship given by Equation (3.45). This method can be extremely useful to estimate the

impact of intra- and interspecic competition for space and resources—for instance, in the frame-

work of zoobenthic community establishment and maintenance (Boström and Bonsdorff 2000;

Hovel et al. 2002).

2782.indb 72 9/11/09 12:05:52 PM

Self-Similar Fractals 73

3.2.7.4 Fractal dimensions, areas, and Perimeters

Although the perimeter and the area fractal dimensions introduced in Section 3.2.7 specically

describe the relationships between the perimeter P and the area A of a patch, they can more generally

be used to quantify the structure of any rough object such as proteins, biological aggregates obtained

from natural environments (for example, marine snow) or bioreactors (for example, bioocculated

microbial aggregates generated by the activated sludge process), inorganic colloidal aggregates (for

example, clays, alum, ferric hydroxides), and growth patterns of inorganic and organic systems (for

example, cluster formation, dendritic growth, diffusion-limited aggregation). However, it appears

that many fractal relationships involving the perimeter or the area of an object signicantly differ

from the concepts introduced above. These relationships are reviewed hereafter and discussed in

relation to the related fractal dimensions.

3.2.7.4.1 Fractal Structure of Surfaces

3.2.7.4.1.1 On the Fractal Surface Dimension of Proteins

The characteristic roughness and corrugation of protein surfaces are of extreme biological relevance

in their function, including (1) the association of different subunits; (2) the recognition, diffusion,

and binding of a ligan; and (3) the release of products. Typically, the surface areas of proteins is

dened by the area accessible to a probe sphere (Lee and Richards 1971; Richards 1977) and the

related fractal surface dimension D

, estimated as

=−2

log

(3.50)

or equivalently

AkR

−2

(3.51)

where k is a constant, A the molecular surface area, and R

the probe radius (Lewis and Rees 1985).

Note that Equation (3.51) is the strict equivalent of Equation (3.6), and consequently of the box-

counting dimension D

described in Section 3.2.2. This approach has been used to investigate the

fractal surface dimension of three enzymes (lysozyme, ribonuclease A, and superoxide dismutase),

which was D

= 2.44 on average for scales ranging from 0.1 and 0.35 nm (Lewis and Rees 1985).

The variation in D

over the protein surfaces revealed high fractal dimensions (D

> 2.5) for surface

regions of lysozyme characterized by elevated reactivity, while lower D

values (D

∈[2.3 − 2.5])

were obtained from regions located near the activity surface of the enzyme (Lewis and Rees 1985).

The region of greatest surface roughness corresponded to the dimmer interface and to the subunit

interface in superoxide dismutase and ribonuclease A, respectively. Regions involved in the forma-

tion of tight complexes and permanent binding (for example, interfaces between subunits, antibody-

combining regions) appeared to be more irregular than average (D

> 2.4). In contrast, regions of

proteins that interact transiently with ligans and cannot tolerate formation of stable complexes (for

example, active sites) appear to be smoother than average. Despite the very narrow range of scales

used to estimate the fractal dimensions and in the absence of any discussion related to the obvious

changes in the values of D

with the size of the probe (Lewis and Rees 1985; see their Figure 2b),

this work indicates that increased roughness favors strong bounds, thus relating the fractal structure

to specic functions and suggesting that fractal dimension could actually be used to predict protein

functional sites, as functional surfaces are much rougher than protein surfaces in general (Pettit and

Bowie 1999). Note that Equation (3.50) has further been modied to account for statistical errors

resulting from local variations in roughness at specic sites on a protein surface as

=−

∑

log

(3.52)

2782.indb 73 9/11/09 12:05:55 PM