Seuront L. Fractals and Multifractals in Ecology and Aquatic Science
Подождите немного. Документ загружается.

x Contents
7 Estimating Dimensions with Condence ............................................................................231
7.1 Scaling or Not Scaling? That Is the Question ..................................................................... 231
7.1.1 Identifying Scaling Properties ............................................................................... 232
7.1.1.1 Procedure 1: R² – SSR Procedure ........................................................233
7.1.1.2 Procedure 2: Zero-Slope Procedure ....................................................234
7.1.1.3 Procedure 3: Compensated-Slope Procedure ......................................238
7.1.2 Scaling, Multiple Scaling, and Multiscaling: Demixing Apples
and Oranges ........................................................................................................... 239
7.2 Errors Affecting Fractal Dimension Estimates ..................................................................241
7.2.1 Geometrical Constraint, Shape Topology, and Digitization Biases ......................241
7.2.2 Isotropy ..................................................................................................................243
7.2.3 Stationarity ............................................................................................................ 243
7.2.3.1 Statistical Stationarity ..........................................................................243
7.2.3.2 Fractal Stationarity ..............................................................................244
7.3 Dening the Condence Limits of Fractal Dimension Estimates ......................................246
7.4 Performing a Correct Analysis ...........................................................................................246
7.4.1 Self-Similar Case ...................................................................................................247
7.4.2 Self-Afne Case ....................................................................................................247
8 From Fractals to Multifractals ............................................................................................249
8.1 A Random Walk toward Multifractality .............................................................................249
8.1.1 A Qualitative Approach to Multifractality ............................................................249
8.1.2 Multifractality So Far ............................................................................................250
8.1.3 From Fractality to Multifractality: Intermittency ................................................. 253
8.1.3.1 A Bit of History.................................................................................... 253
8.1.3.2 Intermittency in Ecology and Aquatic Sciences .................................. 253
8.1.3.3 Dening Intermittency ......................................................................... 253
8.1.4 Variability, Inhomogeneity, and Heterogeneity: Terminological
Considerations ....................................................................................................... 255
8.1.5 Intuitive Multifractals for Ecologists ....................................................................257
8.2 Methods for Multifractals ...................................................................................................260
8.2.1 Generalized Correlation Dimension Function D(q) and
the Mass Exponents t(q) ........................................................................................260
8.2.1.1 Theory ..................................................................................................260
8.2.1.2 Application: Salinity Stress in the Cladoceran Daphniopsis
Australis ...............................................................................................262
8.2.2 Multifractal Spectrum f(a) ....................................................................................262
8.2.2.1 Theory .................................................................................................. 262
8.2.2.2 Application: Temperature Stress in the Calanoid Copepod Temora
Longicornis ..........................................................................................265
8.2.3 Codimension Function c(g) and Scaling Moment Function K(q) ..........................265
8.2.4 Structure Function Exponents z(q) ........................................................................268
8.2.4.1 Theory ..................................................................................................268
8.2.4.2 Eulerian and Lagrangian Multiscaling Relations for Turbulent
Velocity and Passive Scalars ................................................................ 271
8.3 Cascade Models for Intermittency ...................................................................................... 276
8.3.1 Historical Background ........................................................................................... 276
2782.indb 10 9/11/09 12:02:31 PM
Contents xi
8.3.2 Cascade Models for Turbulence ............................................................................278
8.3.2.1 Lognormal Model ................................................................................278
8.3.2.2 The Log-Lévy Model ...........................................................................279
8.3.2.3 Log-Poisson Model ..............................................................................280
8.3.3 Assessment of Cascade Models for Passive Scalars in a Turbulent Flow .............280
8.4 Multifractals: Misconceptions and Ambiguities .................................................................282
8.4.1 Spikes, Intermittency, and Power Spectral Analysis .............................................282
8.4.2 Frequency Distributions and Multifractality .........................................................284
8.5 Joint Multifractals ...............................................................................................................285
8.5.1 Joint Multifractal Measures ...................................................................................285
8.5.2 The Generalized Correlation Functions ................................................................287
8.5.2.1 Denition .............................................................................................287
8.5.2.2 Applications .........................................................................................290
8.6 Intermittency and Multifractals: Biological and Ecological Implications ..........................293
8.6.1 Intermittency, Local Dissipation Rates, and Zooplankton Swimming
Abilities .................................................................................................................294
8.6.2 Intermittency, Local Dissipation Rates, and Biological Fluxes in the Ocean .......296
8.6.2.1 Intermittency, Turbulence, and Nutrient Fluxes toward
Phytoplankton Cells .............................................................................297
8.6.2.2 Intermittency, Turbulence, and Physical Coagulation of
Phytoplankton Cells .............................................................................298
8.6.2.3 Intermittency, Turbulence, and Encounter Rates in the Plankton .......299
9 Conclusion .............................................................................................................................301
References .....................................................................................................................................303
Index ..............................................................................................................................................337
2782.indb 11 9/11/09 12:02:32 PM
2782.indb 12 9/11/09 12:02:32 PM

xiii
Preface
This book originally owed its existence to chance, although it also represents a fair amount
of work. Apart from a brief encounter with fractals as an undergraduate in marine biology
in 1992, through the reading of a paper entitled “Applications of Fractal Theory to Ecology”
by S. Frontier picked up by pure chance on the dusty shelf of a university library, I had never
heard the word fractal and was struggling to nd something really appealing in my studies.
The seed was planted, though, and my main stimulus came a few months later from my very
rst encounter with Professor Serge Frontier. He was to become the mentor—without him,
I would probably never have been offered the chance to try to apply fractals and multifractals
to the characterization of plankton patchiness in turbulent ows for my Ph.D. thesis. His legacy
is everywhere in this volume, and I wish to thank him for his inspirational guidance that has
lasted over the years.
I also greatly beneted from passionate discussions on fractals shared with Christophe Luczak
during the stammering of our scientic careers in the mid-1990s. I am indebted to Jim Mitchell who
persuaded me to turn a rough manuscript into the present book. His friendship and support extend
well beyond the piece of work involved in this volume. A few signicant encounters contributed
to my personal and professional developments, and as such I wish to thank here, Mark Doubell, Li
Hua, Sophie Leterme, Justin Seymour, Yugi Tanaka, Raechel Waters, Dr. Fabian “95%” Wolk, and
Hidekatsu Yamazaki.
I wish to thank John Sulzycki from CRC Press / Taylor & Francis Group for his patience and trust.
Last, but not least, I thank my parents for their indefectible support despite their ongoing struggle
to understand my passion for science.
2782.indb 13 9/11/09 12:02:32 PM
2782.indb 14 9/11/09 12:02:32 PM

xv
About the Author
Laurent Seuront, Ph.D., is a professor in biological
oceanography at Flinders University (Adelaide, Australia)
and a senior research scientist at the South Australian
Research and Development Institute (West Beach,
Australia). His education includes a B.S. in population
biology and ecology from the Université des Sciences
et Technologies de Lille (1992); an M.S. in marine ecol-
ogy, data analysis, and modeling from the Université
Pierre et Marie Curie, Paris (1995); and a Ph.D. in bio-
logical oceanography from the Université des Sciences et
Technologies de Lille (1999). Prior to his present position,
Dr. Seuront was a research fellow of the Japanese Society for the Promotion of Science at the
Tokyo University of Fisheries (1999–2000) and a research scientist at the Centre National de la
Recherche Scientique (CNRS) in France (2001–2008).
Dr. Seuront’s current research concerns biological–physical coupling in aquatic and marine sys-
tem environments, with a focus on the effect of microscale (submeter) patterns and processes on
large-scale processes. Aspects of his work combine eld, laboratory, and numerical experiments to
study the centimeter-scale distribution of biological (nutrient, bacteria, phytoplankton, microphy-
tobenthos, and microzoobenthos) and physical (temperature, salinity, light, turbulence) parameters,
as well as the motile behavior of individual organisms in response to different biophysical forcings.
His work to date has been the subject of over 100 publications in international journals and contrib-
uted books, more than 80 presentations at international conferences, and invited seminars at over 50
locations throughout the world, including at prestigious institutions such as Cambridge University
and the Massachusetts Institute of Technology (MIT). Among multiple awards, Dr. Seuront recently
received the CNRS Bronze Medal in France (2007) in recognition of his early career achievements,
and a prestigious Australian Professorial Fellowship from the Australian Research Council.
2782.indb 15 9/11/09 12:02:33 PM
2782.indb 16 9/11/09 12:02:34 PM

1
1
Introduction
As suggested by the titles of several seminal earlier works, such as The Fractal Geometry of Nature
(Mandelbrot 1983) and Fractals Everywhere (Barnsley 1993), one could expect to nd fractal and
multifractal properties everywhere. This might indeed be the case, as the Science Citation Index
returned more than 12,500 and 1,600 articles respectively containing fractal and multifractal in
their title between 1987 and 2008.
The fractal character of a system has many implications for its properties. In particular, a fractal
set tends to ll the whole space in which it is embedded and has a highly irregular structure, while
it possesses a certain degree of self-similarity; that is, when viewed at increasing levels of magni-
cation, a fractal set appears to be the union of many ever smaller copies of itself (Figure 1.1). This
character is captured by the so-called fractal dimension, D
F
, of the set and can be regarded as one
measure of the complexity of the system and as the degree at which a set lls the Euclidean space
in which it is embedded. The compelling reasons for the emerging fractal theory in many scientic
elds are based on the hope that complex systems could be explained using a relatively low number
of parameters, say, the fractal dimension D
F
.
One of the most illustrative processes where the concept of fractals applies relates to atmospheric
and oceanic turbulence. Originally, the word turbulence referred to the random motion of a crowd,
turba being the Latin for crowd. The complex and self-similar nature of ows is present in the early
work of Leonardo da Vinci (1442–1519). In his study of owing and running water (1508–1510),
he captured the transition from ordered to chaotic uid motions (Figure 1.1A) and the complexity
and self-similar nature of turbulent ows (Figure 1.1B). Later pictorial work by Katsushika Hokusai
(1760–1849) (Figure 1.2A), Utagawa Hiroshige (1797–1858) (Figure 1.2B,C), and Vincent van Gogh
(1853–1890) (Figure 1.2D) clearly expressed the multiscale nature of the surface of the turbulent ocean
(Figure 1.2A,B,C) and atmospheric ows (Figure 1.2D). The self-similarity evidenced by Jonathan
Swift in his satiric verse, “So, Nat’ralists observe, a Flea Hath smaller Fleas that on him prey,
Figure 1.1 Flowing and running water (1508–1510) by Leonardo da Vinci (1442–1519).
2782.indb 1 9/11/09 12:02:35 PM

2 Fractals and Multifractals in Ecology and Aquatic Science
A
B
D
C
Figure 1.2 Turbulence in art. (A) The Great Wave of Kanagawa by Katsushika Hokusai (1760–1849);
(B) Naruto Straight Eddies at Awa; (C) Vortices in the Konaruto Stream by Utagawa Hirshige (1797–1858);
and (D) The Starry Night by Vincent van Gogh (1853–1890).
2782.indb 2 9/11/09 12:02:37 PM
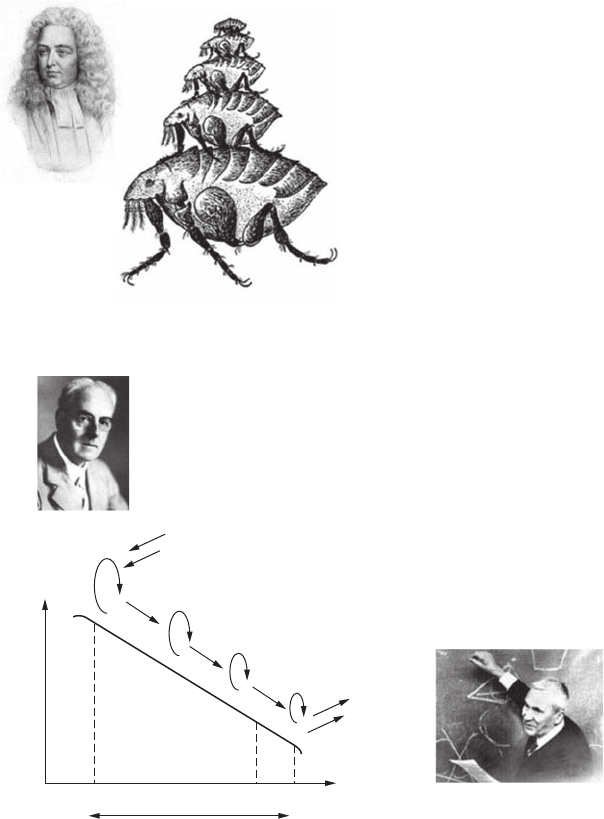
Introduction 3
So, Nat’ralists observe, a Flea
Hath smaller Fleas that on him prey,
And these have smaller yet to bite ‘em,
And so proceed ad infinitum.
A
B
C
Jonathan Swift, 1733
Modified from Hegner, R. (1938)
Big Fleas Have Little Fleas, or Who’s Who Among the Protozoa.
Williams and Wilkins, Baltimore.
Big whirls have little whirls that feed on their velocity,
and little whirls have lesser whirls and so on to viscosity
Lewis Fry Richardson, 1922
Log E(k)
Injection
Log (k)
Viscous
dissipation
Inertial subrange
1/L
1/1
1/1
k
Figure 1.3 The verse of the Irish satirist Jonathan Swift on eas, originally meant as a swipe at lesser poets
(A); parodied by the meteorologist L. F. Richardson to describe the multiscale nature of turbulence (B); which
was later formalized by the Kolmorogov turbulent cascade (C).
And these have smaller yet to bite ‘em, And so proceed ad innitum” (Figure 1.3A), seemingly led to
the crude, but picturesque, seminal description of turbulence by L. F. Richardson (1922), “Big whirls
have little whirls that feed on their velocity, and little whirls have lesser whirls and so on to viscos-
ity” (Figure 1.3B). This qualitative description of fully developed turbulence was later formalized
by the Kolmogorov turbulent cascade, which describes how turbulent kinetic energy generated at
large scales L, cascade through a hierarchy of eddies of decreasing size down to the viscous scale l
k
,
where energy is dissipated into heat (Figure 1.3C). This self-similarity of turbulent ows is clearly
visible from natural and simulated turbulent ows (Figure 1.4), as well as from large-scale patterns
such as von Karman vortex streets and cloud cover (Figure 1.5).
2782.indb 3 9/11/09 12:02:39 PM
