Seuront L. Fractals and Multifractals in Ecology and Aquatic Science
Подождите немного. Документ загружается.

4 Fractals and Multifractals in Ecology and Aquatic Science
More specically, most processes in natural sciences—for example, physical forcings, population
and community dynamics—are sources of heterogeneity and create space-time structures such as
gradients, patches, trends, and other complex patterns (Figure 1.6). Note that natural landscapes are
consistently more complex, exhibiting high levels of structural and organizational complexity that
can barely be compared to man-made landscapes (Figure 1.7). These heterogeneous structures are
particularly well developed in most aquatic environments where resources such as plankton exhibit
patchiness over a continuum of scales. The multiscale variability of marine environments leads to
a view of the ocean as a landscape—that is, a seascape—in the sense that it can be described by
patterns of different temporal and spatial scales. Many physical and biological oceanographers then
relate their ndings to the spectrum of physical processes of circulation patterns in oceanic basins
or large gyres to ne-scale eddies or rips. Ecologists also recognize spatial heterogeneity as a major
factor regulating the distribution of species. Terrestrial and aquatic ecology must deal with scale,
because the objects it focuses on—the organisms and types of environments—are rarely found to
have regular shapes and to be homogeneously distributed through time or space; the “geometry
of Nature” is barely understandable and quantiable in terms of human geometry (Figure 1.8 and
Figure 1.9).
Yet until recently no quantitative or qualitative theory has described the origin, dynamics, and
consequences of heterogeneity in ways that increase the accuracy of predictions about ecological
processes in a complex environment. Dealing with scales has therefore required overcoming the
difculties generated by space-time dependencies associated with the heterogeneous distribution
of ecological variables. Classical statistical theory works well to predict changes in variance due to
different sizes of sampling units or different grains of sampling strategies when the sampling units
are independent. The basic independence of replicates assumption, however, is rarely veried in
natural science, and therefore the use of classical theory is questionable. Moreover, the more tradi-
tional, widely used mathematical descriptors have little meaning in a multiscale spatial context.
AB
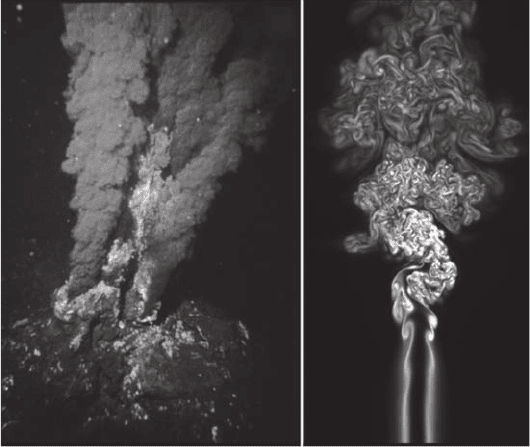
Figure 1.4 Black smoker at (A) a midocean ridge hydrothermal vent and (B) numerical simulation of a
turbulent jet at a Reynolds number of 4500. [(A) From OAR/National Undersea Research Program (NURP),
National Oceanic and Atmospheric Administration. (B) Courtesy of Peter Moore and Bendiks Jan Boersma,
Laboratory for Aero and Hydrodynamics, Delft University of Technology, The Netherlands.]
2782.indb 4 9/11/09 12:02:41 PM
Introduction 5
Scale is undoubtedly one of the central themes of landscape ecology (see, for example, Peterson
and Parker 1998; Wiens 1989, 2001). Most, if not all, of the landscape properties playing a role in
the biology and ecology of populations (such as gradients, patch quality, boundaries, connectivity,
and organism response) change with changes in scale. The notion of scale (sensu lato) is quite broad
and involves a wide range of terms and concepts that can be clustered under key categories such
as heterogeneity, hierarchy, and size. The rst one (heterogeneity) includes spatial patchiness and
temporal variability, and has been acknowledged as an essential property of nature (Kolasa and
Pickett 1991). The second one (hierarchy) is an intrinsic property of ecosystems, which are always
hierarchically organized (O’Neill et al. 1986; Kolasa 1989), and this implies the consideration of
an organizational scale. Finally, the evident, thought widely neglected, size-dependence of species’
A
B
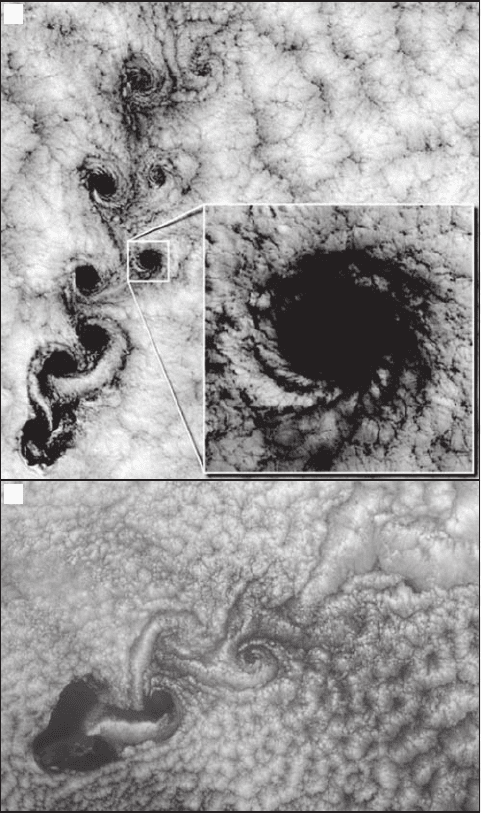
Figure 1.5 Self-similarity in the atmospheric von Karman vortex streets observed off the Mexican coast
near Guadalupe Island on June 11, 2000 (A) and off the Chilean coast near the Juan Fernandes Islands on
September 15, 1999 (B). Also note the self-similarity in cloud patterns. [(A) From Robert F. Cahalan, NASA/
GSFC (see Cahalan et al. 2001, http://climate.gsfc.nasa.gov/viewPaperAbstract.php?id=69). (B) From NASA/
GSFC/JPL.]
2782.indb 5 9/11/09 12:02:43 PM

6 Fractals and Multifractals in Ecology and Aquatic Science
AB
DC
Figure 1.6 Natural landscapes and seascapes. (A) Vertical vegetation zones in Honeur Harbor, France;
(B) a “snail’s-eye-view” of an intertidal rocky shore, Lincoln National Park, South Australia; (C) reefs built by
the colonial tube-polychaete Ficopomatus enigmatus in the Coorong, South Australia; and (D) local alterna-
tion between meadows and thickets, La Cauchie, France.
Figure 1.7 South Australian landscapes, with (A) and without (B) anthropogenic inuences. Both pictures
were taken from an altitude of 20 km. (See color insert following page 80.)
2782.indb 6 9/11/09 12:02:47 PM

Introduction 7
Figure 1.8 Contrast between the complexity of the geometry of nature (A) and the Euclidean geometry of
human architecture (B) in Tokyo (Japan), and an example of self-similarity in Hindu architecture, the Sri Siva
Subramaniya Temple (Nadi, Fiji) in an ensemble (C) and detail view (D).
Figure 1.9 Contrast existing between the geometry of a man-made surface, a brick wall (A) and (B) the bark
patterns of white g (Ficus virens), (C) the English oak (Quercus robur), and (D) the cotton palm (Washingtonia
lifera). (See color insert.)
2782_C001.indd 7 9/11/09 3:26:18 PM

8 Fractals and Multifractals in Ecology and Aquatic Science
features (Peters 1983) is critical to our understanding of how organisms—hence, populations and
communities—respond to the abiotic and biotic properties of their environment. The size of the “win-
dow” through which an organism views or responds to the structure of its landscape (its extent), for
example, may differ for organisms of different body sizes or mobility, and organisms may discern
the patch structure of the landscape within the window with different levels of resolution (grain).
As a result, the organism-dened “landscape” is intrinsically scale dependent (Figure 1.10). Note
that the organisms’ extent and grain dened above fundamentally differ from the measurement
scales imposed by the observer.
In heterogeneous data sets, where estimates of quantities such as biomass vary precisely with the
scale at which measurements are made, fractal dimension then appears to be a useful measure of
space-time complexity and provides several advantages over other descriptive indices of ecological
patchiness. However, despite some insightful description of various possible applications of fractals
in ecology (Frontier 1987; Sugihara and May 1990a; Hastings and Sugihara 1993) and successful
applications in landscape ecology, entomology, and behavioral ecology, they are still hardly ever
used. The situation is even more dramatic for multifractals, where use is often restricted to the elds
of nonlinear dynamical systems, fully developed turbulence, rainfall modeling, spatial distribution
of earthquakes, nancial time-series modeling, and Internet trafc modeling. Applications of multi-
fractals in ecology appear limited to a few papers published over the past 10 years dealing with the
characterization of the dynamics of forested systems (Scheuring and Riedi 1994; Solé and Manrubia
1995, 1996; Manrubia and Solé 1996; Drake and Weishampel 2000, 2001), patchiness of marine
systems (Pascual et al. 1995; Seuront et al. 1996a, 1996b, 1999, 2001, 2002; Seuront and Schmitt
2005a, 2005b; Lovejoy et al. 2001; Seuront and Spilmont 2002), and species-area relationships
(Borda-de-Água et al. 2002).
Two main reasons are suggested for the still very limited applications of fractals and multifractals
in ecology and aquatic sciences. First, the fractal and multifractal formalisms, mainly developed
and used in the elds of nonlinear dynamical systems and physical sciences, might be impenetrable,
at least for ecologists without a reasonable mathematical and statistical background or for those who
do not have the time to devote to such studies. Second, unlike most of the numerical techniques
used to analyze spatial data sets and time series, no software is commercially available for fractals
and multifractals. As a consequence, the main aim of this book is to bridge the gap between the
potentially obscure fractal and multifractal concepts and tools and the end-user ecologists. Fractals
and multifractals have thus been theoretically, mathematically, and practically treated at a level that
is reasonably accessible to the ecologists willing to fully understand and use them. Detailed consid-
erations on the construction and properties of theoretical fractals, such as the Cantor set, Sierpinski
Figure 1.10 Self-similar rabbits, originally used to illustrate concepts in population dynamics. (Courtesy of
Professor M. Bull, Flinders University, Adelaide, Australia.)
2782.indb 8 9/11/09 12:02:49 PM
Introduction 9
gasket and carpet, Pascal triangle, and Koch curve or the Mandelbrot and Julia sets widely investi-
gated elsewhere (such as Peitgen et al. 1992; Schroeder 1991; Barnsley 1993, 2000; Falconer 1985,
1993) were intentionally omitted to put more focus on real case studies.
The book naturally starts with basic denitions and illustrations related to Euclidean and fractal
geometries and dimensions. In particular, a special effort was made to dene the too-seldom-used
concepts of fractal codimension and sampling dimension. In Chapters 3 and 4, the concepts
of self-similar and self-afne fractals are introduced and the fundamental differences existing
between them are discussed, as well as the concepts of statistical self-similarity and statistical
self-afnity. Chapter 5 introduces a family of fractal dimensions derived from frequency dis-
tributions. Chapter 6 has subsequently been devoted to clarify the relationship between fractal
theory and concepts such as chaos theory, strange attractors, self-organization, and self-orga-
nized criticality. In Chapter 7, the intrinsic limitations of fractal analysis are addressed in detail,
and some criteria and easy-to-handle procedures to ensure the relevance of fractal analysis are
provided. In Chapter 8, the concept of a multifractal is dened, the different multifractal analy-
sis techniques available are reviewed and exemplied, and a very intuitive, “without the math”
multifractal technique is introduced and illustrated using a step-by-step procedure applied to a
real case study. The seldom-used joint multifractal framework is also introduced, dened, and
illustrated.
It is nally stressed that the motivation to write the present book stems from a report that non-
mathematically acquainted ecologists might not be able to appreciate the strength of fractals and
multifractals in analyzing their data sets because of the lack of nontechnical—hence, accessible—
books on the subjects. As such, the present work has been thought, designed, and written with
ecologists in mind. It has been written in a “handbook fashion” to promote the understanding and
the use of fractals and multifractals in ecological sciences. More technical sections are nevertheless
provided throughout the text for readers interested in getting into the (more mathematical) details of
fractal and multifractal techniques. As a consequence, it is, of course, statistically and mathemati-
cally colored. As such, the readers willing to get the details behind what could be referred to as the
“fractal/multifractal black box” can understand where a given equation comes from. However, what
ecologists do care about is ecology! Most of the techniques presented and discussed here have then
been illustrated with concrete examples from recent works but mostly using original data sets to
allow the readers to understand what they could get out of fractal and multifractal analysis without the
hassle of going through the math, or at least before eventually feeling the need to go through the math.
The less-mathematical readers will hopefully nd the hooks they need to appreciate the strength
and usefulness of fractals and multifractals in the eld of ecological sciences. Each example has
been treated as a short paper, including a description of the species and the system considered, and
the experimental procedures used to get the data, before presenting their results and discussing
them in an ecological context. More generally, the relevance of fractals and multifractals to describe
branched patterns and growth processes, habitat complexity, organism distribution, behavioral pro-
cesses, predator–prey and population dynamics, turbulent processes, and species diversity and evo-
lution are reviewed, exemplied, and discussed.
2782.indb 9 9/11/09 12:02:50 PM
2782.indb 10 9/11/09 12:02:50 PM

11
2
About Geometries
and Dimensions
2.1 From euclidean to Fractal geometry
The geometries of shores, rocks, plants, waves, hydrodynamic ow, organism trajectories, and
many other natural phenomena are important in different scientic disciplines, and each eld
tends to adapt specic concepts to describe the complexity of Nature. Ecological models often
approach natural shapes as simple geometrical approximations. Lakes are approximated as cir-
cles, particles as spheres, patches as squares and rectangles, and trees as cones (Figure 2.1). Many
patterns and shapes in Nature, however, are so irregular and fragmented that they present not sim-
ply a higher degree but an altogether different level of complexity, as compared with Euclidean
approximations. Curves, surfaces, and volumes in Nature can thus be so complex that ordinary
measurements become meaningless. Mandelbrot (1977, 1983) coined the term fractal geometry,
introducing a new concept that has rapidly provided a unifying and cross-disciplinary basis to
the description of Nature’s complexity. Many natural phenomena have a nested irregularity and
may look similarly complex under different resolutions (for example, turbulent water ow or
clouds) (Figures 2.2 and 2.3). Although this nested structure, referred to as scale invariant, could
be thought of as an additional source of complexity, it becomes a source of simplicity in fractal
geometry.
A
B
Figure 2.1 Illustration of the fundamental differences between human schematic depictions (A) of natural
forms such as trees (B).
2782.indb 11 9/11/09 12:02:52 PM
12 Fractals and Multifractals in Ecology and Aquatic Science
1000 1500 2500 3000 3500 4500 5000
0
10
–6
10
–8
10
–7
10
–6
10
–8
10
–7
10
–6
10
–8
10
–7
2000 3000 4000 6000
40002000
2000 2500 3000
Time (ms)
Dissipation Rate ε (m
2
·
s
–3
)
3500 4000
1000 5000
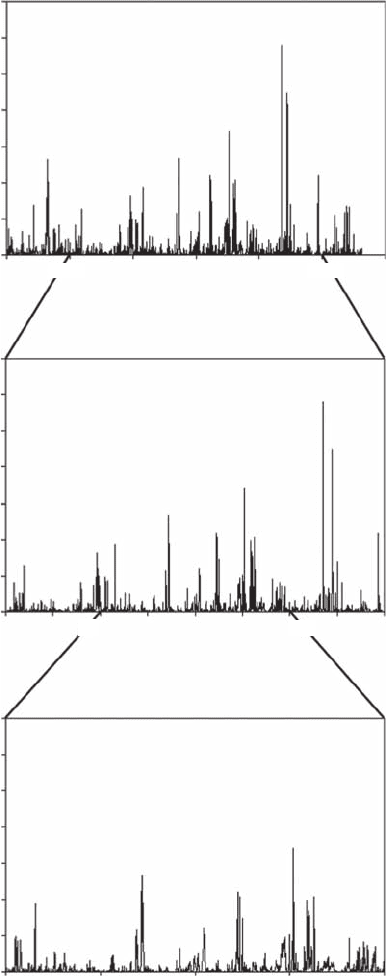
Figure 2.2 Nested structure perceptible in time series of microscale turbulent kinetic energy dissipation
rates (m
2
⋅ s
−3
). At increasing resolution, the local and global structures remain very similar.
2782.indb 12 9/11/09 12:02:54 PM

About Geometries and Dimensions 13
Scale invariance means that the observed structure remains unchanged under magnication or
contraction. A scale-invariant pattern is thus scale dependent and cannot be characterized by a
single scale. Fundamental to most denitions of fractals is then the idea of “measurement at scale
d.” For each d, we measure a set in a way that ignores irregularities of size less than d, and we see
how these measurements behave as d → 0. For instance, if one considers a plane curve C, then the
measurements, M(d), might be the number of steps required by a pair of dividers set at length d to
traverse C. In case of a fractal, the relationship between the measurements M(d) and the scale d must
obey a power-law form:
M(d) = kd
-f
(2.1)
where k and f are empirical constants, the constant f being referred to as the scaling exponent.
Taking logarithms, Equation (2.1) can be written as:
log M(d) = log k − f log d (2.2)
These relationships are appealing for computational and experimental purposes, since f can be
estimated as the slope of a log-log graph plotted over a suitable range of d, and k is the intercept (see
Figure 2.4A). Over a wide range of scales—typically many orders of magnitude—the same rela-
tionships among critical structural and functional variables are maintained. One may nevertheless
note that for real phenomena, we can only work with a nite range of d. In the ideal case, theory and
experiment diverge before an atomic scale is reached, but practically, there may be several scaling
regions, separated by breakpoints, that are fractal within each region but failing when a breakpoint
is crossed (Figure 2.4B). This question will be studied more thoroughly in Chapter 7. Such similar-
ity is said to be fractal, and the relationship among variables can be described by a fractal dimension
or a power law. Although the concept of fractals is fairly new (Mandelbrot 1983), the use of power
functions to characterize scaling laws has a venerable history.
Figure 2.3 Nested structure perceptible in the geometry of clouds. At increasing resolution, the local and
global structures remain very similar. (See color insert following page 80.)
2782.indb 13 9/11/09 12:02:55 PM
