Seuront L. Fractals and Multifractals in Ecology and Aquatic Science

Подождите немного. Документ загружается.

14 Fractals and Multifractals in Ecology and Aquatic Science

In particular, the use of power laws is so well established that they are called allometric equa-

tions (McMahon and Bonner 1983; Schmidt-Nielsen 1984). They are of the form:

y = ax

(2.3)

where y is some dependent variable, a is a normalization constant, x is some independent variable

(typically a body mass), and b is referred to as the scaling exponent introduced above.

Biological scaling relationships are called allometric because the exponent, b, typically differs

from unity. If b = 1, the relationship is called isometric, and it plots as a curve on linear axes. When

b ≠ 1, the relationship is called allometric, and it plots as a curve on linear axes. However, power

functions have the nice property that they are linear when plotted on logarithmic axes. This is read-

ily seen by taking the logarithms of both sides of Equation (2.3)

log y = log a − b log x (2.4)

which is conceptually equivalent to Equation (2.2). This is equivalent to the equation for a straight

line, where the dependent variable, log y, is equal to an intercept, log a, plus the product of the

slope, b, times the independent variable, log x. As stated above for Equation (2.2), the scaling expo-

nent of the power function is the slope of the linear plot on logarithmic axes. The mathematical

Log M (δ)

Log δ

Log k

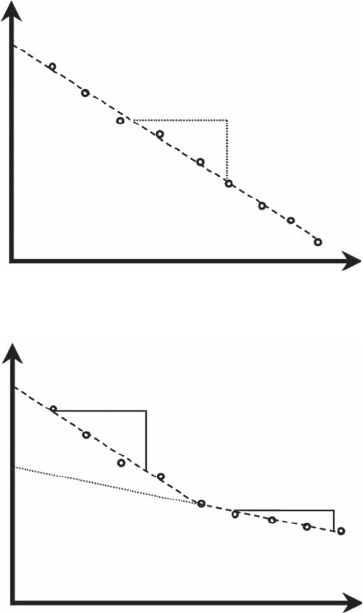
Figure 2.4 Schematic illustration of the expected behavior of M(d) vs. d in a log-log plot in case of a single

scaling regime (A) and multiple scaling (B). The slope of the linear parts of the graph provides an estimate of

the scaling exponent f.

2782.indb 14 9/11/09 12:02:57 PM

About Geometries and Dimensions 15

equivalence of Equations (2.3) and (2.4) means that it is fairly straightforward to derive empirical

allometric relationships by using a least-squares regression technique to t a linear regression to

log-transformed data. We will, nevertheless, see in Chapter 7 that great care must be exercised to

choose the appropriate regression procedure.

The most familiar example of allometry is simple geometric scaling. If we have spheres or any

objects of self-similar shapes, one can describe changes in surface area, A, or volume, V, as a func-

tion of a linear dimension, the radius, r, as follows:

A = pr

(2.5)

and

Vr=

(2.6)

in which the scaling exponents are the dimensions of the objects. In addition, if the objects maintain a

constant density as they vary in size, then the mass, M, is proportional to the volume, V (that is, M ∞ V),

and we can express their linear dimension, L, or surface areas, A, as functions of their mass M as:

L = c

1/3

(2.7)

and

A = c

2/3

(2.8)

where the values of the normalization constants, c

and c

, depend on the units of measurements.

Since the same equations apply to any shape, if living organisms preserve self-similar shapes as

they vary in size (Peters 1983; Schmidt-Nielsen 1984), then their linear dimensions and their sur-

face areas should vary as one-third and two-thirds of their body mass respectively, but with some

intrinsic restrictions.

Although the power laws shown in Equations (2.7) and (2.8) provide sharp limits on the form

and metabolic requirements of many families of living organisms, organisms do not usually exhibit

such simple geometric scaling as expected, for example, in the ideal case of size-nested painted

wooden dolls from Russia. This is because there are powerful constraints on structure and function

that do not allow organisms to maintain the same geometric relationships among their components

as size changes over several orders of magnitude. This was pointed out by Galileo, who noticed that

some laws of physics and biology are not necessarily unchanged under changes of scale. Referring

to the strength of bones, he argued that an animal twice as long, wide, and tall will weight eight

times more. He nevertheless pointed out that bones that are twice as wide have only four times the

cross-section and can only support four times the weight. Thus, to support the full weight, bone

width must be scaled by a factor greater than 2. This deviation from simple similarity introduces a

natural scale in the design of organisms, both animal and vegetal, land bound and aquatic. At some

roughly predictable size, the bones become larger than the rest of the animal, and scaling breaks

down; see Haldane (1928). For instance, as trees increase in size, the cross-sectional areas of their

trunks and the total surface areas of their leaves increase more rapidly than expected from purely

geometric considerations, as M

3/4

rather than M

2/3

. The differential increase in trunk area provides

for mechanical resistance to buckling due to gravity and wind, while the scaling of leaf area allows

for increased gas exchange to support the increased phytomass. Similarly, as mammals increase in

size, there is a differential increase in the thickness of their bones to provide mechanical support

and in the surface area of the lungs to provide gas exchange for metabolism. Another well-known

2782.indb 15 9/11/09 12:02:58 PM

16 Fractals and Multifractals in Ecology and Aquatic Science

instance of scaling in biology is the energy dissipation of homeothermic animals as a function of

their weight or mass. A “naïve” approach would expect the energy dissipation, E, to be proportional

to the animal’s surface area, which for similar animals is proportional to the two-thirds power of its

volume or mass M (see Equation 2.8), leading to E = C

2/3

where C

is a constant. However, it appears

that larger animals dissipate more energy than the relation E = C

2/3

would predict. The data for a wide

variety of species, ranging from unicellular organisms to whales, are much better tted by an exponent of

3/4 (Peters 1983; Schmidt-Nielsen 1984), suggesting that larger animals are less energy efcient.

Although the origin and the phenomenological relevance of the previous allometric (scaling)

exponents have been widely discussed elsewhere (Brown and West 2000), one must note here from

the comparison of Equations (2.5) and (2.6) with Equations (2.1) and (2.3) that the scaling exponents

f and b are conceptually similar to a fractal dimension. Before going further into the renements

of fractal geometry, I will discuss extensively the meaning of what we usually call a “dimension”—

with regard to “dimensions” in the fractal framework specically—and some related concepts.

2.2 dimensions

2.2.1 E

u c l i d E a n , To p o l o g i c a l , a n d Em b E d d i n g di m E n s i o n s

2.2.1.1 euclidean dimension

We learn from an early age that lines and curves are one-dimensional, planes and surfaces are two-

dimensional, and solids such as a cube are three-dimensional. The concepts refer to the traditional

Euclidean geometry and Euclidean dimension. More generally, any space that can be conceived

of has a characteristic number associated with it called a dimension. But what is a dimension?

Surprisingly, despite the a priori naïve character of the question, it is far from being easy to provide

a complete denition of dimension.

A denition of dimension could be the number of real-number parameters needed to

uniquely describe all the points in a space. Thus, the real-number line is one-dimensional as

it only takes one parameter to describe each point. Dimension is invariant so that a plane, for

example, requires two parameters in rectangular (x, y) or polar (r, q) coordinates. Other suitable

examples come to mind. The set of lines in a plane is two-dimensional, as describing any one

of them uniquely requires two parameters: the slope and y intercept or the x and y intercepts,

for example. The set of all circles in a plane is three-dimensional (two for the coordinates of the

center and one for the radius), and the set of all conic sections in a plane is ve-dimensional.

More formally, we say a set is d-dimensional if we need d independent variables to describe a

neighborhood of any point.

Another way to think of dimension is as the degree of freedom available within the space

(see, for example, Grassberger 1983; Hentschel and Procaccia 1983). Physical (Euclidean) space is

three-dimensional because there are three independent directions that objects within the space

can move (up/down, left/right, and forward/backward). The surface of the Earth, on the other

hand, is two-dimensional, as we are only free to move in one of two directions (left/right and

forward/backward). Any vertical motion is the result of moving in the other two directions. Under

these constraints, a countable set of points is now zero-dimensional as we have zero degrees of

freedom. It is not possible to move through such a space from one point to another without leav-

ing the space.

2.2.1.2 topological dimension

From earlier work in topology, the dimension of any set can be dened as one greater than the

dimension of the object that could be used to completely separate any part of the rst set from the rest.

A line has thus a dimension 1 since it can be separated by a point (0 + 1 = 1), a plane has dimension

2782.indb 16 9/11/09 12:02:59 PM

About Geometries and Dimensions 17

2 since it can be separated by a line (1 + 1 = 2), and a volume has dimension 3 since it can be sepa-

rated by a plane (2 + 1 = 3). This notion of dimension is called the topological dimension D

of a

set (Hurewicz and Wallman 1941; Dugundji 1966). Strictly speaking, the topological dimension of

any set is dened as one greater than the dimension of the object that could be used to completely

separate any part of the rst space from the rest. However, when referring to composite sets such

as an x-shaped set (×) or the union of a point and a lled circle (· •), the above denition seems,

however, incomplete. Indeed, locally the former set is one-dimensional except at the intersection

of the two segments where it becomes zero-dimensional (that is, a single point), and thus is obvi-

ously one-dimensional. The latter is a bit more challenging, as it is a union of completely separated

components, where the point component (·) is zero-dimensional while the circle component (•) is

two-dimensional.

Introducing the concepts of local dimension and global dimension, one can thus characterize the

composite set (· •) via the local dimensions of its components. To get the global dimension of the

set, the above denition needs to be slightly modied. The dimension of any set should be the maxi-

mum of its local dimensions where the local dimension is dened as one more than the dimension

of the lowest-dimensional objects needed to separate any neighborhood of the space into two parts.

According to this denition, the composite set (· •) is indeed two-dimensional.

More practically, the dimension of the union of nitely many sets is the largest dimension of any

one of them, so if we “grow grass” on a plane, the result is still a two-dimensional set. We should

nevertheless note here that if we take the union of an innite collection of sets, the dimension can

grow. For example, a line, which is one-dimensional, is the union of an innite number of points,

each of which is a zero-dimensional object.

2.2.1.3 embedding dimension

There can nevertheless occasionally be a little confusion about the dimension of an object. Sometimes

people call a sphere a three-dimensional object because it can only exist in space, not in the plane.

However, a sphere is two-dimensional. Any little piece of it looks like a piece of the plane, and in

such a small piece, you only need two coordinates to describe the location of a point. More formally

speaking, this is only a different measure of dimension, called the embedding dimension D

: A

set has embedding dimension D

if D

is the smallest integer for which it can be embedded into

without intersecting itself. Thus, the embedding dimension of a plane is 2 and the embedding

dimension of a sphere is 3, even though they both have (topological) dimension 2.

A topological property of an entity is one that remains invariant under continuous, one-to-one

transformations or homeomorphisms. A homeomorphism can best be envisioned as the smooth

deformation of one space into another without tearing, puncturing, or welding it. Throughout such

processes, the topological dimension does not change. A sphere is topologically equivalent to a

cube since one can be deformed into the other in such a manner. Similarly, a line segment can be

pinched and stretched repeatedly until it has lost all its straightness, but it will still have a topologi-

cal dimension of 1.

The meaning of dimension can be questioned, however, when dealing with geometric constructs

initially referred to as “mathematical monsters.” For the sake of illustration, consider two case-

study mathematical constructs (Figure 2.5). First, we consider the Koch curve, or Koch snowake

(Koch 1904, 1906). To build the Koch curve (Figure 2.5A), consider a triangle. First, take each line

segment and divide it into thirds. Second, place the vertex of an equilateral triangle in the middle

third, copy the whole curve, and reduce it to 1/3 its original size. Place these reduced curves in

place of the sides of the previous curve. This procedure is subsequently iterated n times. With each

iteration, the curve length increases by a factor of 4/3. An innite repeat of this procedure would

send the length off to innity. Such a geometric construct is unusual but not disturbing regarding

the above denition of dimension.

2782.indb 17 9/11/09 12:03:00 PM

18 Fractals and Multifractals in Ecology and Aquatic Science

This is not the case, however, with the second construct investigated here, the Peano curve

(Schroeder 1991) (Figure 2.5B). First, take a square and divide it into four identical copies of the

original. Second, draw a line starting in one square so that it passes through the center of every other

square until it returns to the starting position. Iterating this procedure n times leads to a curve so

twisted that it has innite length. The resulting object is specically referred to as a Peano monster

curve (Mandelbrot 1983), so called because of its monstrous or pathological nature; note the refer-

ence to the demiurgical nature of such objects. More remarkable is that it will ultimately visit every

point in the initial square. This construct thus generates a one-to-one mapping from the points in the

unit interval to the points in the unit plane. An object with topological dimension 1 can then be trans-

formed into an object with topological dimension 2. This iteration procedure could also be imple-

mented in a cube and would ultimately lead to a space-lling curve (Gilbert 1984). Simple bending

and stretching should leave the topological dimension unchanged, however. These apparently para-

doxical results thus raise questions about the meaning of dimension, especially when one knows that

the Koch and Peano curves are both regarded as basic examples of geometrical fractals.

2.2.2 Fr a c T a l di m E n s i o n

What about the dimension of the so-called fractal objects? For example, what is the dimension of

the Koch snowake (Figure 2.5A)? It has topological dimension 1, but it is by no means a curve; the

length of the “curve” between any two points on it is innite. No small piece of it is linelike, but

neither is it like a piece of the plane or any other d. In some sense, we could say that it is too big to

Figure 2.5 Building process of two theoretical fractals: the Koch snowake (A) and the Peano curve (B).

2782.indb 18 9/11/09 12:03:02 PM

About Geometries and Dimensions 19

be thought of as a one-dimensional object but too small to be a two-dimensional object. Maybe its

dimension should be a number between one and two. In order to make this kind of thinking more

precise, one must look at the dimension of familiar objects another way.

Strictly speaking, a mathematical fractal is dened as any patterns for which the dimension

exceeds the discrete topological dimension (Mandelbrot 1977, 1983). Formally, the concept of scal-

ing exponent dened above can be extended and generalized through the concept of Hausdorff

dimension (Carathéodory 1914; Hausdorff 1919), which can be regarded as the “core” of a whole

family of fractal dimensions. The Hausdorff dimension D

of a subset S embedded in an Euclidean

space of dimension D

(that is, S ∈ D

) arises from asking “What is the size of S?” Note that this question

is fairly general and can be applied to a wide variety of sets as “How long is S?” referring to the length of

a coastline or the Koch curve, “How large is S?” referring to the surface of an island or a vegetation patch,

or “How big is S?” referring to the volume of a cloud or a sponge. The answer comes from counting the

number of open balls needed to cover the set S (Figure 2.6). For each d > 0, consider N(d) the smallest

number of open balls of radius d needed to cover S. One can then show that the limit:

=−

(

)

→

lim log()/log

δδ

(2.9)

exists (see, for example, Mandelbrot 1977). D

is the Hausdorff dimension of the set S. Equation (2.9)

is equivalent to the approximate power law

()

δδ

≈

−

(2.10)

Figure 2.6 Hausdorff dimension of a set S. The Hausdorff dimension D

is estimated from counting the

number of open circles of radius d needed to cover the set S, where d → 0.

2782.indb 19 9/11/09 12:03:05 PM

20 Fractals and Multifractals in Ecology and Aquatic Science

where k is a constant and

≈

refers to an asymptotic behavior. Equation (2.10) must then be written

as “N(d) scales asymptotically as d

−D

,” or more loosely as “N(d) scales as d

−D

.” Although several

equivalent denitions can be found in the literature (see, for example, Rogers 1970; Federer 1969;

Falconer 1985) (Figure 2.7), the generality of the Hausdorff dimension makes it difcult to com-

pute and to determine its properties (Mandelbrot 1977, 1983). In particular, the intrinsic asymptotic

condition, d → 0 (compare this to Equations 2.9 and 2.10), is difcult to fulll in most applications.

More practical methods devoted to estimate fractal dimensions can be found in Chapters 3 and 4.

Hereafter, we will thus refer to the more general fractal dimension D

It can be understood that a fractal is a complex geometrical shape, constructed of smaller copies

of itself. The fractal dimension D

subsequently quanties how the “size” of a fractal set changes

with decreasing observation scales. However, while geometrical objects in Euclidean geometry are

described using integer dimensions (0 for a point, 1 for a line, 2 for a plane, and 3 for a volume),

fractal dimensions are not necessarily an integer and may take values between the boundaries of

integer topological dimensions. Topologically, a line is one-dimensional. The dimension D

of a

fractal pattern on the plane, however, is a continuous function with range 1 ≤ D

≤ 2. A completely

B E

δδ

Figure 2.7 Different ways of estimating the Hausdorff dimension D

of a set S. The number N(d) (see

Equation (2.10), is taken as (A) the least number of circles of radius d that cover S; (B) the greatest number of

disjointed circles of radius d with centers in S; (C) the least number of boxes of radius d that cover S; (D) the

number of boxes of size d that intersect S; and (E) the least number of sets of diameter at most d needed to

cover S. In all cases, the procedure is iterated until d → 0.

2782.indb 20 9/11/09 12:03:09 PM

About Geometries and Dimensions 21

differentiable series has a fractal dimension D

= 1 (the same as the topological dimension), while

a Brownian motion completely occupies two-dimensional topological space and therefore has a

fractal dimension D

= 2. Fractal dimensions 1 ≤ D

≤ 2 quantify the degree to which a pattern lls

the plane. In the same way, a planar curved surface is topologically two-dimensional, while a fractal

surface has dimension 2 ≤ D

≤ 3.

Consider now a measure unit dened as d

; for D

= 1, 2, and 3, one refers to a length, a surface,

and a volume, respectively expressed in m, m

, and m

. Following Equation (2.10), a given set S

thus measures N(d)d

≈ d

“meters at the power (D

− D

).” A set S characterized by a fractal

dimension D

= 2 will then have a nite surface (D

= 2), while its length (D

= 1) will be innite,

and its volume (D

= 3) nil. When D

is a noninteger, length, surface, and volume become useless to

characterize S because these metrics are nil or innite.

So what is the dimension of the Koch snowake? For such a self-similar mathematical fractal

(we will see in Chapter 3 that the fractal concept can nevertheless be signicantly complex) that

can be divided into N similar parts, each of which is a copy of the whole reduced k times, the fractal

dimension D

can simply be written as

log

(2.11)

In the case of the Koch snowake (Figure 2.5A), each part of the “curve” can be decomposed into

four rescaled copies of itself, contracted by a linear factor of 3. Equation (2.11) thus leads to a fractal

dimension D

= 1.262 for the Koch snowake. Consider now two other basic geometrical fractal

objects: the Sierpinski carpet and gasket (Figure 2.8). Each component of the Sierpinski carpet and

gasket can be decomposed into eight and nine copies of itself, contracted by linear factors of 3 and

4, respectively. The related fractal dimensions are then D

= 1.893 and D

= 1.585 for the Sierpinski

carpet and gasket, respectively. In other words, the Sierpinski carpet covers space more intensively

than the Sierpinski gasket and the Koch curve. One must nally note that any set exhibiting integer

fractal dimensions can simply be thought as a specic case of fractal patterns. The fractal dimen-

sion can thus be thought of as a measure of sparseness of any set embedded in a Euclidean space.

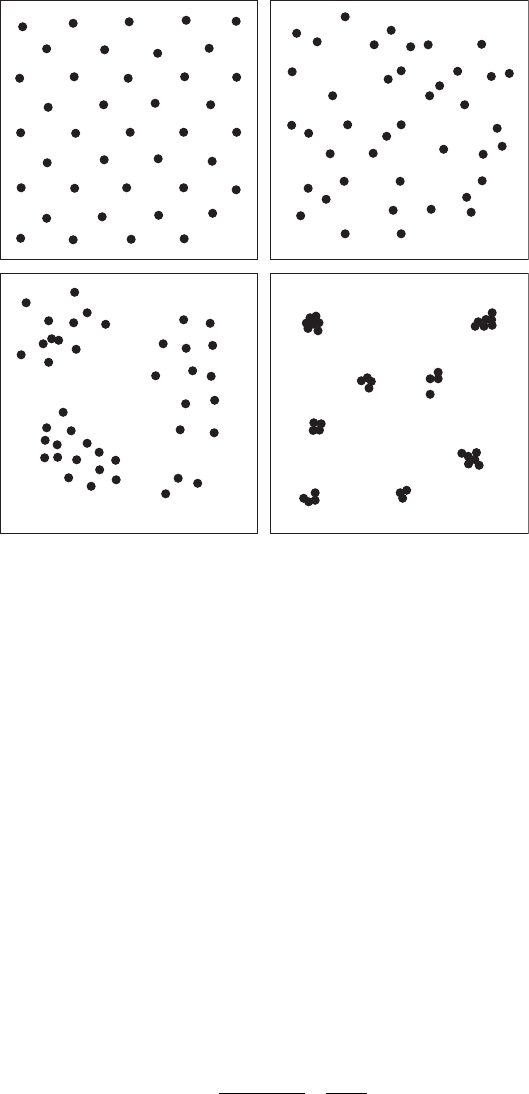
Consider a set embedded in a two-dimensional space. Homogeneous, regularly spaced sets will

then be characterized by a higher fractal dimension than more sparse sets (Figure 2.9). At the

limit, a plane-lling set has a fractal dimension D

= 2, while the fractal dimension of a set so

sparse that it is reduced to a single point is nil, D

= 0 (Figure 2.9). These different statements can

nevertheless be rened with the introduction of the concepts of fractal codimension and sampling

dimension.

Figure 2.8 Building process of two theoretical fractals: the Sierpinski carpet (A) and the Sierpinski gasket (B).

2782.indb 21 9/11/09 12:03:12 PM

22 Fractals and Multifractals in Ecology and Aquatic Science

2.2.2.1 Fractal codimension

Consider a set S characterized by a fractal dimension D

embedded in a space of topological dimen-

sion D

. The fractal codimension, c

, of the set S is given by:

= D

− D

(2.12)

The fractal codimension thus appears as a measure of the relative sparseness of the set S, while the

fractal dimension is a measure of its absolute sparseness. As a consequence, Koch and Sierpinski

constructs considered in a plane or in a three-dimensional space have the same fractal dimension,

while their codimension is increased a unit. The fractal codimension can thus be regarded as being

a more fundamental measure than the fractal dimension, especially in a probabilistic framework

where it can be introduced directly.

Consider the number of open balls of radius d needed to cover a set S. The probability Pr(B

∩ S)

for a ball B

to intersect S is given by:

Pr()

()

NB S

∩≈

∩

≈≈

−

(2.13)

where N(B

∩ S) [

NB S

()

∩≈

−

(see Equation 2.10) is the number of balls B

intersecting S, and

N(B

) [

()

≈

−

] is the total number of boxes. It is straightforward from Equation (2.13) that the

most infrequent events are characterized by the highest fractal codimensions and thus the lowest

Figure 2.9 Fractal dimensions and codimensions of different point patterns. (A) Regular point pattern,

= 2 and c

= 0; (B) random point pattern, D

= 1.8 and c

= 0.2; (C) random clumped point pattern, D

= 1.4

and c

= 0.6; and (D) aggregated clumped point pattern, D

= 1.1 and c

= 0.9.

2782.indb 22 9/11/09 12:03:16 PM

About Geometries and Dimensions 23

fractal dimensions (see Figure 2.9). One may note here that Equations (2.12) and (2.13) are equiva-

lent when c

≤ D

, or equivalently D

≥ 0. Equation (2.13), however, does not imply any constraint

on the fractal codimension c

. When c

> D

, Equations (2.12) and (2.13) thus lead to D

< 0. This

statement is totally inconsistent with the essence of a fractal dimension, dened as a strictly positive

measure (Mandelbrot 1977, 1983) (see, for example, Equations (2.1), (2.2), (2.9), (2.10), and (2.11).

A purely geometrical denition is no longer satisfactory in a probabilistic framework where the

effective dimension of the probability space is a function of the sampling effort.

2.2.2.2 sampling dimension

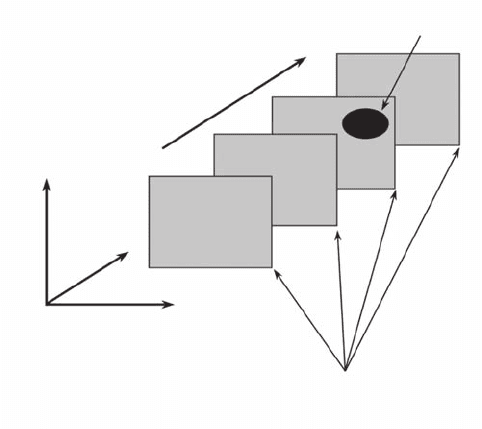
Mainly for practical reasons present in most scientic areas, statistics implicitly deal with samples

of nite size. The dimension of the probability space can nevertheless increase with the number of

independent samples considered (Figure 2.10). Considering N

independent samples of dimension

, the related quantity of information can be expressed as:

N × N

= d

−

)

(2.14)

where D

is the sampling dimension (Seuront 1998) dened as:

≈ (log /log )−

(2.15)

In particular, Equations (2.14) and (2.15) show that the dimension of the probability space can be

increased above D

(a single sample) and to overcome the a priori paradoxical limitation related

to the occurrence of negative fractal dimensions. Thus, considering a rare event S such as c

> D

Equation (2.12) can be rewritten as:

= D

+ D

− c

(2.16)

Probability Space

Physical Space

Independent Realizations

~ δ

–D

Figure 2.10 Sampling fractal dimension. Considering an increasing number of independent realizations

) increases the effective dimension of the probability space. The probability of nding a set S embedded

in a D

-embedding space increases with N

. One may also note that as N

→ +∞, the entire probability space

is explored.

2782.indb 23 9/11/09 12:03:19 PM