Schlechta K. Nonmonotonic Logics: Basic Concepts, Results, and Techniques
Подождите немного. Документ загружается.


84 CHAPTER 2. PREFERENTIAL STRUCTURES
2) If (~ r X E X and #(X) = #t(X) = 0, then no <
a,i >• Ntx
is minimal in
Ntx,
so, as
Nto = Me, .$4 t
is not X-stoppered.
Let all jr4 - X-coherent sequences be constant under #~, so (by Lemma 2.102)
all < a, A~ > satisfy (+b). By Lemma 2.87, A~ [a = Av~ [a, so nit < a, Av~ >
satisfy (+b). So all < a,~ > satisfy (*b) by Lemma 2.105, b., so for each a,
there is KJt= X-nice, such that ~4~c~ [a = A~:,, [a (Lemma 2.97, b.). Einkaufen:
Croissants, pain aux noix, grosse boule, fromage, confiture aux abrieots, Berna-
chon, C6te-R6tie. Let ~4 ! be the full cpm constructed from < KI~ : a E if/it >
in Lemma 2.89, then for all
a E Mc Apc,o [a = A~c~, [a
(Lemma 2.89), thus
~4jc~, [a = A~ [a and 3d ~ M ! (Corollary 2.88).
Niceness was defined relative to a given 3/t, but as # = #t, niceness with respect,
go 3d and niceness with respect to ~d r are equivalent. So we can argue: Looking
at the construction in Lemma 2.89, we see that for a ~ Mo there,/s =/C~' is
X-nice, and for a E M0 ~' =
{Me}.
By condition 2),
-~Ic
is X-nice. So all
K~ t are X-nice, 3,41 is full, so 3d r is X-stoppered by Lemma 2.93. []
2.1o7 Limit preferential models
Introduction
The main result (soundness and completeness) of this Section 2.1.7 is given in
Theorem 2.113. As a matter of fact, it is not very nice, carrying too much burden
of the semantical construction. It should thus be considered as a first step to
more appealing representation results. Yet in may be said that in particular the
seemingly contorted condition (e) is- with exception of (/3)(4) - something to be
expected: It expresses the connection to classical logic via a suitably closed subset
of the classical models and is also an adaptation of the definability preservation
condition in [Sch90] and [Sch96-1], (/3) is a version of cnmulativity between unit
cumulativity, i.e. TIN ~ --~ (T[~ r ~-* T, r '~b), and general cumulativity, i.e.
T I ~ @ for all ~b E Tl --+ (T I N ~b ~ T U TI [~ ~b), which says that any stronger
theory, whose models form a suitably closed and minimizing set, has the same
consequences. The failure of "OR" and of one half of the Deduction Theorem is a
direct consequence of the closure condition and our definability postulate, which
says that suitable initial segments have to correspond to some stronger theory
Tt. If we drop this definability condition, however, we seem to have to work with
dense sets of models (in the standard topology), and it is unclear to the author
how to arrive then at any Iogical characterization.
Some notation
Definition 2.107 Given !~, let [T, T~]~ abbreviate T/k T and for all TIt such
that
Tt ~ Tit P T
and all qS, T t" 4~ iff Tl/I~ ~, i.e. T, Tl define an interval of
IN -equivalent theories.

2.i. PREFERENTIAL STRUCTURES
85
We shall consider structures, whose base set M consists of pairs < rn, i >, where
m is a classical s i an index. Small variables x, Y, .. 9 will range over such
pairs < m, i >6 M, we write m, etc. to denote its first element.
The results
Definition 2.108 Let JM =< M,-<> be a set M of indexed classical E-models
< m,i >, with a transitive binary relation -4 on M. For simplicity, we assume
that each s occurs at least with one index i.
We shall further assume that
(a) if < m/,# >-<< m,i > and <
mr, i, >E M,
then also <
mr, i,
>-<< m,i >,
i.e. logically equivalent models have same successors (but not predecessors[).
Let A := AM be the set of pairs of s < T, T! > such that
(i) T! V T
(ii) Tt is downward closed in T (in jt4): For no z :< m, i >6 M, zt =< ml, # >E
M, rm E M(T,), m E M(T) - M(Tt)
we have x -4 xt.
(iii) Tt minimizes T: For all z =<
rn, i
> with
m E M(T) - M(Tt)
there is
zt =< mq it > with m/E
M(Tt)
and zt ~4 z.
(iv) Each
m E M(T)-M(TI)
"sees" all mt E M(Tt): For each m E
M(T)-M(TJ
and rn/E
M(TI)
there are indices i and/t such that < rm,//>~4< rn, i > (by (a)
then for all such i').
We further assume that
(b) all pairs y -< x are the composition of "useful" information in the sense
of A, i.e. there is an descending chain z = x0 >-- xl ~- ... ~- x~ = y, with
< T{, T;+~ >E a and m~. E M(T{) -M(T{+J, m~{+ 1 E M(T/+~).
Given such Ad and A~, we define T ~M r iff there is < T, Tt >E Am with
TI ~-4. []
We note the following immediate
Fact 2.109 For any A := AM as above, we have
(a) < T, T >E A for all s T,
(b)<T, TI>EAand<T,T">EA~ <T,T/UT,>EA,
(c) <T,T!>EA and <TI, T/I>EA~ <T,T/t>EA,
(d) <
T, TI
>E A and TI ~- Tit ~- T ~ <TIt,
Tt >6 A,
(e) <T, Tt>EAand <T,,S>EA, andT/~-Tttl-T~ <T, TIUS>EA.
Proof The proof is straightforward, we have to check (i) - (iv).
(a) trivial.
(b) Set S := Tt 12 T//. (i) is trivia!.
(ii) Suppose to the contrary there are z -< x/with
'm~: E
M(T) - M(S)
and
m:~, E
M(S). So m~, E
M(TI) N M(Tu),
and m~ C
(M(T) - M(TI) ) U (M(T) - M(T,)).
But both cases (for 'm~) yield a contradiction to (ii) of the prerequisites.
(iii) Fix z with mx E
M(T)-M(S).
Suppose m~ ~
M(TI).
By (iii), we find z --< x
with mz E
M(TI).
If
mz ff M(TII),
we find by (iii) xl --< z with m~, E
M(T,).
By

86 CHAPTER 2. PREFERENTIAL STRUCTURES
transitivity, xl -~ x, and by Tt/b T and (ii), rn~, E M(Tt). The case .rn~ ~ M(Ttl)
is analogous.
(iv) Let m E M(T) - M(S), and xll with rn~, E M(S) = M(TI) N M(TII). If
m f[ M(Tt), then we find < m,i > with x;t << rn, i > . Otherwise, we find
suitable < rn, i/> for Tll.
(c) Note that by Tll [- TI, M(TIt) C_ M(TI). (i) is trivial.
(ii) Suppose x ~ ztt, m~,, E M(Ttt), rn~ E M(T) - M(rll). If rn~ ~
M(T~),
we
have a contradiction to (ii) for < T, TI >, if rn~ E M(Tt) - M(Ttt), we have a
contradiction for < TI, Tit > .
(iii) Let rn~ E M(T) - M(Tu). If rn~ ~ M(Tt), we find xt -,( x with 'rn~, E M(Tt).
If rn~, E M(Tt) - M(TIt), we find xtt -~ xl, rn~,, E M(Ttt), by transitivity xtt ~ z.
If rn~ E M(TI) - M(TII), the result is immediate.
(iv) Let rn E M(T) - M(Ttr), and zH with rn~,, E M(TH)
c M(T~). If m
M(T) - M(T~), we are done, so we are if rn E M(Tt) - M(TII), in each case by
(iv).
(d) is trivial
(e) (i)is trivial.
(ii) Let xl with rn~, E M(T~) n M(X), 9 with rn~ E M(T) - M(TI U S). If
m~ r M(TI), we are done. Suppose then rn~ E M(Tr) - M(S), but then by
T! I- TI! rn~: E M(Ttl), and we are done again.
(iii) Let x with rn, E M(T) - M(TI U S). If rn~ r M(TI), we find z -~ x, rn~ E
M(Tr If rn~ ~ M(S), then by M(T~) c M(T~), we find ~ -~ ~, m~, ~ M(S). By
transitivity, x~ ~ x, and by (ii) for < T, T~ > and S ~- TH F T, rn~, E M(T~). If
rn,= E M(Tt)-M(S), then rn~ E M(Tt~)-M(S), and we find xZ-.4 x, 'rn~, ~ M(S).
Again, rn,,, E M(T@
(iv) trivial. Cl
Corollary 2.110 (a) T [- 4) --~ T ~ 4;,
(b) T ~M r and T ~M r T ~M 4;A 4;t,
(c) {4;: T ~M 4;} is closed under [-,
(d) < T, T~ >~ AM ~ [T, T~]~.
Proof Immediate from above Fact 2.109:
(a) by (a) of Fact 2.109, (b) by (b) of Fact 2.109. (c) follows from (b) of this
Corollary and the definition of ~M . (d): Let then T! [- Tu I- T. Suppose
T ~M 4;, so for some S, S [- 4; and < T,S >E A. But then < T, TI U S >E A by
(b) of Fact 2.109, and < TIt,TtU S > by (d) of Fact 2.109, so Ttt ~M 4. K, on
the other hand, Ttt ~M 4;, then for some S, S t- 4; and < Tit, S >E A. But then
< T, TI U $ >E A by (e) of Fact 2.109 and so T ~M 4;. []
Example 2.4 Neither OR (ffl~ ~b, ~/I,-~ ~ =~ 4;V 4;tl--~ ~b) nor one half of the
Deduction Theorem (T,r '• =~ T(~ 4; --~ ~) hoIds:
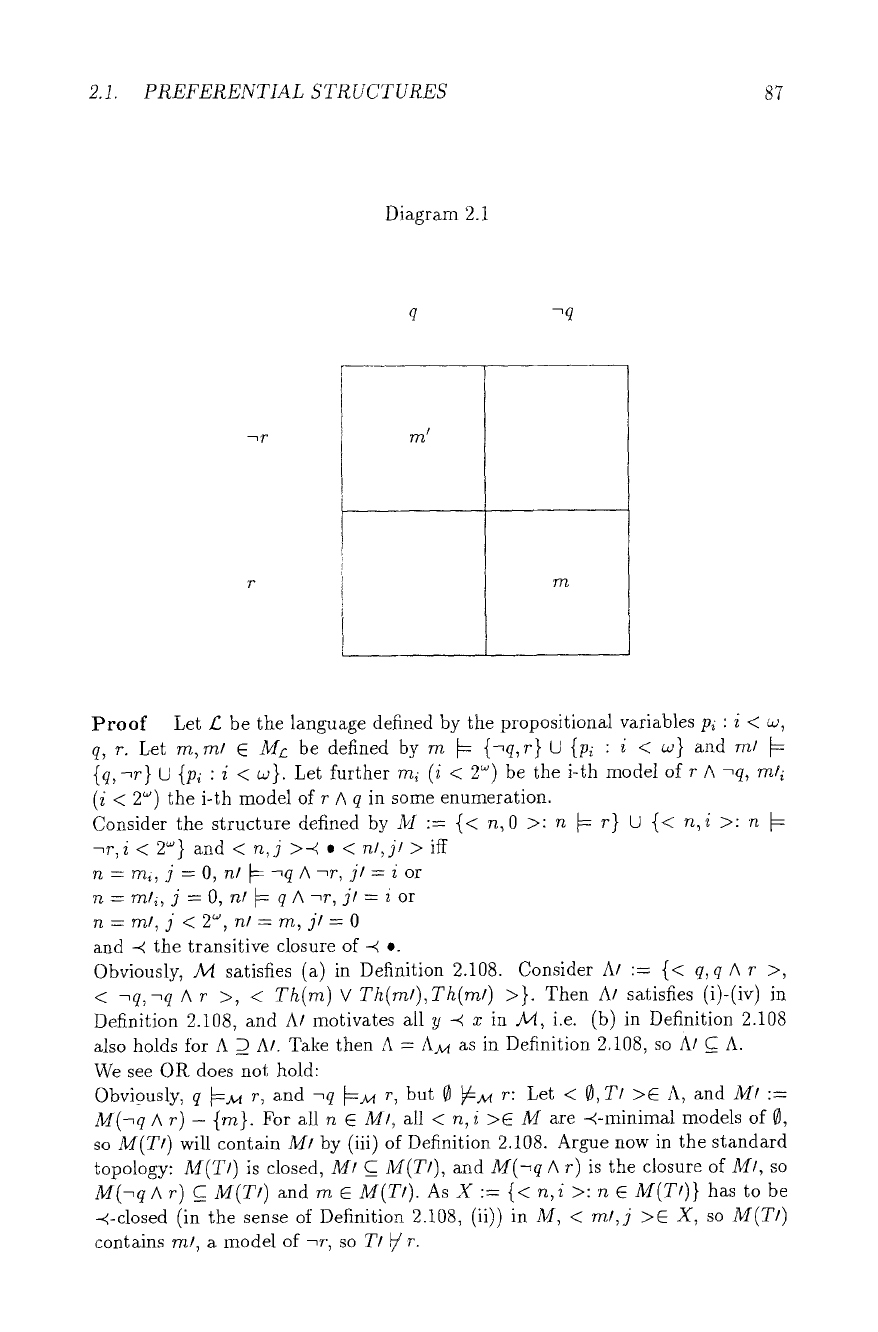
2.1. PREFERENTIAL STRUCTURES
87
Diagram 2.1
q ~q
m /
Proof Let/2 be t}~e language defined by the propositional variables Pi : i < co,
q, r. Let rrz, rn/
E ML
be defined by rn ~ {~q,r} U {Pi : i < co} and rn/
{q, ~r} U {p~ : i < co}. Let further m~ (i < 2 ~) be the i-th model of r A -~q, ml~
(i < 2 ~ the i-th model of r A q in some enumeration.
Consider the structure defined by M := {< n,0 >: n ~ r} U {< n,i >: n
~r,i
< 2 ~} and <
n,j >-d 9 < hi,j1
> iff
n = m~, j = 0, n/~ -~q/x ~r, jt = i or
n = rnli, j = 0, nl ~ q A -~r, jl = i or
n=rar ~',n/=rn,jI=0
and -< the transitive closure of --< 9
Obviously, M satisfies (a) in Definition 2.108. Consider At := {<
q,q A r >,
< ~q,o,q A r >, < Th(m) V Th(ml),Th(m~)
>}.
Then AI satisfies (i)-(iv) in
Definition 2.108, and Al motivates all y -< z in 34, i.e. (b) in Definition 2.108
also holds tor A __D Ar Take then A = AM as in Definition 2.108, so Ar C A.
We see OR does not hold:
Obvigusly, q ~a r, and ~q ~4 r, but 0 ~ r: Let < ~,TI >E A, and Me :=
M(-~q A r) --
{ra}. For all n E MI, all < n, i >E M are --<-minimal models of 0,
so
M(T~)
will contain Mt by (iii) of Definition 2.108. Argue now in the standard
topology:
M(TI)
is closed,
MI C_ M(Tt), and M(-~q
A r) is the closure of MI, so
M(~qA r) C
M(TI)
and ra E
M(Tt).
As X := {< r~,i >: n E M(T,)} has to be
--<-closed (in the sense of Definition 2.108, (ii)) in M, <
rul,j
>E X, so
M(Tt)
contains rn/, a model of ~r', so T/~ r'.

88 CHAPTER 2. PREFERENTIAL STRUCTURES
T, r ~,u ~ => T ~a r --~ ~P does not hold:
We work in the same example, and show that q ~:v, r, but not ~ ~,~ -~q V r. As
above, for any < O,TI >E A, M(TI) contains rn, so rnl, a model of q A -~r. []
Definition 2.111 (a) E is called a system of/2-pairs, iff E is a set of pairs of
E-theories < T, Tl > such that Tl t- T,
(b) A system E of g-pairs is called a full system of s -pairs, iff (1) For all T,
ewithTI ,-~ r <T,T/>E EwithTIk-r for all< T, Tt>E Ewe
have IT, T@.
(c) For a system E of/2-pairs, and two g-models m, ml define m/<t .r.m iff there
is < T, Tt >E E with m E M(T) - M(T~), ml e M(T@
(d) Let <s be the transitive closure of <1 .~ .
Note that <1.~ and <s are definable in logic from E, through correspondence
between models and complete theories, and m ~ T iff Th(m) t- T. []
Fact 2.112 Let f14 and A = A3a be as in Definition 2.108.
(a) y -~ x ~ my <a rn~,
(b) rn <A m/implies that there is j/such that for all j < m,j >-<< mr > .
Proof (a) A as defined in Definition 2.108 is a system of/2-pairs. Let y -~ x,
we then have by Definition 2.108, (b), y = ,% -4 ... -4 Xl -< a:0 = x, where
m,;~ E M(T~)-M(T~+~), m,;~+~ E M(Ti+I), and < T/, T/+I >E A. So rn~,+~<1.hm,,,
and rn~ <A m~.
(b) Let m <a rnl. So there is a finite sequence m = rn~ <1%... <1%rnl <1 .am0 =
me, with mi E M(T~) - M(Ti+~), mi+~ E M(TI+~) for suitable < T~,Ti+~ >E A.
By Definition 2.108, (a) and (iv), we find jl such that < rni+~,ji+~ >~< rn~,ji >
for all ji+~ and thus, by transitivity, we find suitable jl.
Theorem 2.113 Let IN
be ~
logic which satisfies
(a) Con(T) -+ Con(~),
(b) T=T/-+T=TI,
(c) T is closed under F,
(d) T c ~,
(e) there is a full system E of/2-IN -pairs which
(c~) is compatibel with closure under <e: For no < T, TI >~ E, ml E M(Tt),
m ~ M(T) - M(rr) m <~ 'ml,
(13) satisfies the following condition:
If T, Tt are such that
(1) T, k- T,
(2) TI is closed in T: For no mt E M(Tt), m E M(T) - M(TI) m <~ rrJ,
(3) each copy of each m E M(T) - M(TI) is minimized by some rn! E M(Tr):
For each rn E M(T) - M(T~) there is < T,~,TI,~ >E E such that m E M(T~) -
M(Tt,~) and Vn E M(TI,,) 3rnl E M(TI) such that rn/<~ n or rn/= n,
(4) For each 'ml E M(TI) and m E M(T) - M(TI), there is a copy of x, which is
above 'rnt: gm E M(T) - M(Tt) Vml E M(Tt) .mr
<sm
then IT, T{]~.

2.1. PREFERENTIAL STRUCTURES
89
Then it has a representation by a limit model 34 as defined above in Definition
2.108, and vice versa.
Proof We first show that the consequence relations ~M of Definition 2.108
satisfy indeed above conditions (a)-(e).
(a) holds by (iii) of Definition 2.108, (b) is trivial, (c) is Corollary 2.110, (c), and
(d) is Corollary 2.110, (a).
We turn to (e). Let A := A~. We show that A is a suitable system, satisfying
(a) and (/3). By Corollary 2.110, (d) for <
T, Tt >~
h
[T,T/]~,
so A is a full
system of Z;- ~ -pairs.
(a) : Suppose < v, rt >C A, ra, E
M(T/), ra 6 M(T) -
M(Tt), m <A ml. By
Fact 2.112, (b), there is then jl such that for all j <
ra,j
>-<<
rat,j/
>, so Tl
will not be closed in T, contradicting (ii) of Definition 2.108.
(/3) : It suffices to show that such T, Tt satisfying (1)-(4) of (/3) have the prop-
erties (i)-(iv) of Definition 2.108, so < T, Tt >E A, and by Corollary 2.110, (d)
(i) T/~- T is immediate by (1).
(ii) Suppose there are z -< zt with
ra~, 6 M(Tt), ra,: E M(T) - M(T@
By Fact
2.112, (a), ra~ <A ra=,, contradicting (2) of (/3).
(iii) Tt minimizes T: Let
rn E M(T) - M(Tt),
then we have by (3) of (/3)
< T,,~,Tt,~
>6 A such that
rn 6 M(T,~)-M(Tt,,~)
and Vn 6
M(Tt,,~)~mt 6 M(TI)
such that rat <an or rat = n. If rat <n n, by Fact 2.112, (b) there is then for
each
n E M(Tt~) - M(Tt)
j(n) such that for all jt <
ml, jt
>-<<
n,j(n) > .
Let now < ra, i > be given. By Definition 2.108, (iii) for <
T,,~,Tt~
>, we
have some <
n,j
>-<<
m,i
> with n 6
M(Tf,~). If n E M(Tf),
we are done.
Otherwise, by (a) of Definition 2.108, <
n;j(n)
>-<< ra, i > too, so by transitivity
< ra/,jt
>-<<
ra,i
> with
rat E M(T/).
(iv) Let
ra 6 M(T) - M(Tt), z/
with
ra=, E M(T@
We have to find i such that
z/-<< ra, i >. By (4) of (/3),
ra~,
<A 'ca. By Fact 2.112, (b), there is i such that
z/--<< ra~i > .
We turn to the converse and construct a suitable model 3d =< M, -<> for such
a logic from (an arbitrary system) E, as given by (e):
For ra 6 ML consider { < ra, f >: f E II{M(T/) :< T, Tt >6 E, m 6
M(T) -
M(Tt)} }
and set < ~,g >-~ 9 < ra, f > iff n
6 ran(f). Let -~ be the transitive
closure of -< ..
Note <
n,9 >-< 9 < m,f > ~ n <1 .Era,
and, consequently, < n, 9 >-<<
m,f >---+n<2m.
Proof of Note
<n,g>-<,<m,f>~nEran(f)--+3<T,T/>EEwith
rae M(T) - M(TI), n ~ M(T/) ---~ n <I .~m. []
(Note)
A = AM contains E : We have to check the conditions (i)-(iv) in Definition

90 CHAPTER 2. PREFERENTIAL STRUCTURES
2.108 for all < T, TI >E E. (i) is trivial. (ii) Assume there are < m,f >-4<
ml, fl > with rnl E M(TI), m E M(T) - M(TI). By our above Note, m <z ml,
contradicting (e), (c~). (iii) and (iv) are trivial by construction.
Obviously, (b) in Definition 2.108 is already satisfied by E, -~ is transitive, and
< n,g >~< rn, f > iff < n,gt >-~< rn, f >, so (a) in Definition 2.108 is satisfied
too. Thus, 3,t is indeed a structure as in Definition 2.108.
(a) T [,'- ~5 -+ T >ca r Let T I" r Let E be the full system of s -pairs E
JM is constructed from, so there is < T, TI >E }~ with TI ~- 6. But, as just shown,
E <_ A, so T ~4 r
(b) T ~ 4--+ TIN r So there is T1with < T, TI >E A = AM, Tr b- r so
by (d) T/I r It sumces to show
the conditions (1)-(4) of (/3) for E, as then
IT, T{]~, and thus TI.-~ r
(1) is trivial.
(2) Suppose to the contrary that there is ml E M(TI), m E M(T) - M(Tf),
m <z mL Thus we have a finite sequence m = m~ <1 9 9 - 9 <1 9 <1 9 = ml.
So there are < Ti, ~+~ >E E with m~ E M(Ti) - M(Ti+~), m~+~ E M(7}+~). But
then, by construction of M, there is f,~ with < rn, f~ >E M, ra~+~ E ran(f~), and
< mi+l, f/+l i>-~ 9 < mi, fi >, as -d 9 was defined only by the condition m~+l E
ran(f/). So < rn, fn >=< rnn, f~ >-4< mo, f o >=< 'ml, fo >, contradicting
condition (ii) for ~,ta 9
(3) Suppose to the contrary, that we have some m E M(T) - M(TI) without
any < T.r~, Tr,~ >E P, such that rn E M(T~) - M(Ts~) and Vn E
M(T~=)
3rnl E M(TI) such that ml <z n or m/= n. So for each < T,~,Ts~ >E P, with
m E M(Tm) - M(TI,~) we have n E M(TI,~) - M(T~) without any m~ E M(Tr
such that m~ <r. n. Take f, which always chooses those n, so, by construction
of 3/t, < m,f >E M. We show that we do not find < m~,fl >-<< m,f >,
m~ E M(T~), contradicting (iii) of Definition 2.108 for T~. Suppose to the contrary
we have a chain in ~v4 < m~,f~ >=< m~,r >-< .... -< 9 < m~,f~ >-< 9 <
m0, f0 >=< m,f > with m~ E M(T@ By definition of f and m~ E ran(f),
m~ ~ M(T 0 and we have no r~z E M(T~) with n~ <z rn~. But then, by above
Note, < m~, fr >r rrh, fl >, contradiction.
(4) We have to show that Vine E M(T~)Vm E M(T) - M(TI) mr <~ m. By (iv)
of Definition 2.108, we find for alI m E M(T) - M(T~) and me E M(Tr i, i~ with
< m~,it >-<< m,i >, so by above Note rut <~ rn. []
2.2
Local and global metrics for the semantics
of counterfactual conditionals
2.2.1 Introduction
The semantics for counterfactua! conditionals employs indexed relations -% be-
tween possible worlds, with x -4~ y read intuitively as "x is closer to a than is y."
This Section considers the question how far these different "closeness" relations
of a model may be derived from a common source. Despite some welt-known

2.2. MODELS FOR COUNTERFACTUAL CONDITIONALS
91
negative observations, we show that there is also quite a strong positive answer.
The main result is that for any model equipped with modular relations derived
from multiple metrics d~ via the equation z ~ y iff
d~(a, z) < d~(a, y),
there is
a model that validates exactly the same formulae of the logic of counterfactuals,
and whose relations -G are determined by a common metric d, via the equation
z ~ 9 iff
d(a, z) < d(a, y).
General perspective This Section is an essay on the expressive strength
of the language of counterfactual conditionals describing its models in the Stal-
naker/Lewis semantics of closest worlds.
On the one hand, the main result of this Section (Theorem 2.120) shows that
the language of counterfactual conditionals cannot distinguish between models in
which the distance (or closeness) of worlds is defined by several me_trics - in the
extreme case by a distinct metric for each world - and models where distance is
defined by a single global metric. More precisely, we show that for each model
of the first kind, one can construct a model of the second kind in which exactly
the same formulas of the language of counterfactual conditionals hold. The proof
makes essential use of the fact that, by the very definition of the truth of the
conditional 4; >> ~b in a single world in terms of "closest worlds where S holds",
the closest S-worlds "fence off" nil more distant worlds where S may also hold -
all we "see" is the closest, inner layer of S-worlds surrounding the given world.
On the other hand, we show by a simple example (Example 2.5) that the language
of counterfactual conditionals is expressive enough - given uncountably many
propositional variables - to be able to force models to contain an uncountable
well-ordered set of ever closer worlds. We show that there is an (uncountable)
theory in an uncountable language such that each of its models contains a world
which is approached by an uncountable descending well-order of other worlds.
The "trick" is to keep changing the antecedent S of the conditional S >> ~b, so
that the S-worlds do not hide the St-worlds of another conditional S/>> ~bl.
Beyond the contrasting nature of these results - one shows an expressive weakness,
the other a strength - they are linked together as follows. It is easily shown
(Observation 2.117) that every countable model for counterfactual conditionals
in which the closeness relations are ranked and centred, can be constructed by
defining distance through local metrics, and thus, by our main result, by a global
metric. Consequently, this is also the case for each model for a language of
counterfactual conditionals that has finitely many propositional variables. On
the other hand, the example mentioned in the preceding paragraph shows that
a language for counterfactual conditionals with uncountably many propositional
variables does not always permit models whose closeness can be expressed via a
metric: the set of reals with its natural order does not contain any uncountable
well-orders. The intermediate case of languages with countably infinite many
propositional variables remains to be studied. It is not known to the authors
whether all - or which - constructions of semantics for counterfactual conditionals
can in that case be carried out with countable structures, so as to be covered by
above result of constructibility through a global metric - given rankedness and

92
CHAPTER 2. PREFERENTIAL STRUCTURES
centredness. If one restricts oneself to logics with single formulas on the left hand
side, i.e. of the form ~ 1~ ~b - in contrast to T f~ % where T is an arbitrary
set of formulas - there seems to be a certain possibility as the number of pairs
r ~ and qilgL ~b to be constructed or destroyed is countable. But this is left
to further investigation.
Historical remarks and introduction The central idea of the semantics of
counterfactual conditionals, as developed by Stalnaker [Sta68], Lewis [Lew73] and
subsequent authors, is that a formula c~ >>/3 holds in a world a (of a given model)
iff/3 is true in all of the a-worlds (of that model) closest to a. The basic concept
of the semantics is thus one of "relative closeness", sometimes called "relative
similarity" or conversely "relative distance". It is given formal representation
in various equivalent ways, notably by a family of indexed two-placed relations
-<~ between worlds, with z -~ y read intuitively as "x is closer to a than is y."
Usually the relations -~ are assumed to be modular (i.e. such that there is a
function f from the field of the relation into a totally ordered set preserving the
relation in both directions), in which case we also call the model itself
modular.
From both a philosophical and a mathematical point of view, it is natural to ask
whether the different relations --% of "relative closeness to a" of a model may be
derived in some way from a common source. At first sight, the outlook appears
bleak, for two reasons, both of which can already be found in Lewis [Lew73].
First, we cannot simply identify the relations -% of a model with each other. For
if we take seriously the interpretation of z -4~ y as "z is closer to a than is y,"
then since it is hard to see how any x 5r a can be closer to a than is a itself,
it is customary to impose the constraint of "weak centering" that never x ~ a.
Clearly the only weakly centred models that identify all the relations -4~ with
each other are the trivial ones in which all the relations -% are empty.
Second, and again from the point of view of the ~ntuitive interpretation, it may
be argued that for at least some models the relations should be ldt totally inde-
pendent of each other, for "closeness" as seen from the standpoint of one possible
world need have little in common with closeness as seen from another world.
Now, in such a model, there will not exist any common (or global) metric d that
determines it in the sense that for all worlds
z,y,a
in the model, z -~ y iff
d(a, z) < d(a, g).
For whereas the relations of such a model are quite independent
of each other, the existence of such a global d creates connections. For example, it
forces a -% c whenever b -4~ c and a ~o b, since
d(a, b) < d(a, c) = d(c, a) < d(c, b)
implies by the transitivity of < over the reals'and symmetry of a metric that
d(b, ,~,) = d(a, b) < d(c, b) = d(b, c),
Without contesting the above observations, we shall show that there is still quite a
strong sense in which a common source may be found. Call two models
equivalent
iff they validate exactly the same formuiae of the language of counterfactua!
conditionals. Whilst the relations -~ of a given modular model may not have a
common source, there is "usually" an equivalent model whose relations do have
one. To be precise (Theorem 2.126) for any modular and centred model with at
most countably many worlds, there is an eqnivalent model whose relations -4~

2.2. MODELS FOR COUNTERFACTUAL CONDITIONALS 9.3
are all determined by the same, common metric d, via the equivalence displayed
above,
The first step towards this result is to show (Observation 2.117) that for every
modular and centred model with at most countably many worlds, each of its
relations is determined by some metric. Then we show that we may transform
these "local" metrics into a "global" one. To be precise (Theorem 2.120) given
any model (of any size) equipped with relations each of which is determined by
a metric, we can construct an equivalent model, whose relations are determined
by a common metric.
Some general comments may help place these results in perspective, particularly
as regards harmony with Lewis' philosophical outlook, constraints on cardinality
in the formulation of the results, and potential syntactical applications.
Although our results are positive, they are consistent with the intuitive interpre-
tation of the relation z -<a y and the philosophical perspective of Lewis that are
outlined above. Whilst, as Lewis contends, in a given model closeness as seen
from one world may have little to do with closeness as seen from another world,
our Theorem 2.126 shows that under appropriate hypotheses, we can always find
another model where the closeness relations do have a common origin, and which
validates the same formulae of the language of counterfactual conditionals.
Theorem 2.120 places no restriction on the size of the carrier of the model, i.e. how
many possible worlds it contains. On the other hand, both Observation 2.117 and
Theorem 2.126 require that the model be countable. This constraint is important.
Example 2.5 shows that both of those results can fail in an uncountable model
for an uncountable language.
Clearly, our results are all model-theoretic, but they raise the question of potential
syntactic applications. One would like to be able to prove results of the kind:
such-and-such a well-known logic T for counterfactuals, defined syntactically, is
characterizable by a set of models each of which has all of its "closeness" relations
determined by a common metric. More generally, one would like to be able to
obtain results of the kind: every logic T for counterfactu~is that satisfies certain
syntactic conditions (e.g. contains such-and-such formulae and is closed under
such-and-such rules) is so characterizable: By our Theorem 2.126, to obtain
such a result, it is enough to show that the logic T is characterizable by a set
of modular, centred, countable models, i.e. that for for every tbrmula r ~' T,
there is a modular, centred and countable model that validates T but does not
validate 4. Now, for certain specific well-known counterfactual logics T, there are
in the literature completeness theorems to the effect that for all $ {g T there is
a modular, centred model validating T but not r But it is not clear how far
the constructions in those completeness theorems already guarantee, or may be
adjusted to guarantee, countability of the model produced. That question calls
for further exploration, which will not be attempted in this Section.
We recall essential definitions in Section 2.2.2. For more background on the logic
of counterfactual conditionals, the reader is referred to e.g. Lewis [Lew73], Nute
[Nut84], or Makinson [Mak93]. For real-valued distance functions (metrics) and
topology in general, see e.g. Kelley [Ke175] or Engelking [Eng77].
