Schlechta K. Nonmonotonic Logics: Basic Concepts, Results, and Techniques

Подождите немного. Документ загружается.

104

CHAPTER 2. PREFERENTIAL STRUCTURES

s (i.e. for all A, B C s which, very likely, will finally have properties similar ~o

those of the original definition of extension of [FLM90].

2.3.6 A final example

In Sections 2.3.2 and 2.3.5, we chose a relatively brutal approach: E.g. in Section

2.3.2, we measured A~, globally comparing the p~'s and rds contained in it. This

served to decide on

al__[l

formulas of A~. We now give a more subtle technique,

looking at the individual "proofs" of the r E A~, and show how to define this

way a supraclassical cumulative inference operation.

Let s :=

{p~,q~,r~,si:

i < co}, and consider first closure under p~ t ~-, q~, p~ I" r~,

pi]~ si, q~lN s~:

A := A U {q~: p~ E A} U {ri: p~ E A} U {s~:

p, E A or

q~ E A} and set as above

Ao := A,

A~i+i

A2i._~,

A2i+2 := A2i+l,

A~ := I.J{A~ : i < co}.

We encode now in an ATMS-like fashion (the for us important part of) the proofs

of r E A~ from A by simultaneous induction on the length of proof:

For r E l; - A~, set B A := O.

Let now r E A~, and ~r be a proof of r from A = Ao.

Case 1: r E A0 (Tr the empty proof): Set b; := ~.

7ri

Case 2: The last step of ~r is r A ... h r I- r classically. By induction, br is

defined, where ~r~ is the branch of ~r proving ~. Set b; := U{b;i : i _< n}.

Case 3.1: r = qi, and the last step of ~r is p~ 1~-, q~. Set b~ := b ~p~, where ~r! is the

subproof of ~r, showing

pi.

Case 3.2: r = r~, and the last step of 7c is p~ I~ rl. Set b; := b;,f (~rt as above).

Case 4.1: r =

sl,

and the last step of~r is p;lN s~. Set b; := U'Up, {i}.

Case 4.2: r = s;, and the last step of ~r is q~ I" s4. Set b; := U'q, U {i}.

We thus encode the uses of

p~l~ si, qil

~ Si.

For technical convenience, we close

upwards and define B 2 := {a C co: there is a proof ~r of r from Ao, and b; C_ a}

for r E A~. Obviously, for A C A/,

B 2 ~ B2'.

Set

I A

:= {i : r~ E A~} and

b > t A

iff Vi E

bVj E IA.i >_ j.

(Thus, in particular,

>_ I A.

Note that

b, bl > I ~ ~ bUbt > IA.)

Set finally A := {r E &o:

We now show as usual:

1) A~A,

2) x ~ A -+ A+x = A.

[]

Chapter 3

Defaults as

quantifiers

generalized

3.1 Introduction

We first describe the framework of IBM's

LILOG

project, in which our treatment

of defaults was integrated, give then the formal definitions and results on the

N'-system semantics and the proof theory for the generalized quantifier V, and

finally present our theory revision approach.

Defaults in the LILOG framework

IBM Germany's Stuttgart LILOG project was a natural language (LILOG = Lin-

guistics + Logic) project, "simulating" a travel guide. A German text describing

a city (D(isseldorf) is fed into the computer, and natural language questions can

then be asked about the city. Typical sentences and questions are e.g. (in transla-

tion) "The Hetjens Museum was inaugurated in 1909 and is situated in the Palais

Nesselrode, which was built in the 18th century." and "Where is the Hetjens Mu-

seum?". Of course, there are hard linguistic restrictions on texts and questions,

but these need not concern us here. Typical nonmonotonic information in the

present context is e.g.: "Museums are normally closed on Mondays", "Buildings

normally have windows", connected by "hard" (= classical) information as: "All

museums are buildings", but also exceptions in the sense of "This museum is not

normally closed on Mondays".

More precisely, LILOG's knowledge representation language is an order sorted

language, a (logically equivalent, but computationally non-trivial) extension of

first-order predicate calculus, see [BHRg0]. Sorts are e.g. "Streets", "Buildings",

"Museums" etc. They are partially ordered by set-inclusion. This inclusion re-

lation is determined by one component of the inference system, We can assume

it as given and fixed. (In particular, it is monotonic - in contrast to defeasible

inheritance, where the subset relation is itself defeasible.) There is hard infor-

mation beyond the subset relation, represented by classical first-order formulas,

as "Museums have entrances", and "soft" (= default) intormation. The default

106

CHAPTER 3. DEFAULTS AS GENERALIZED QUANTIFIERS

Diagram 3.1

Flyers

Birds Penguins

Tweety

information is ~appended" to sorts as in the examples above, to :'Museums" and

~Buildings", it speaks about the elements of those sorts,

Obviously, conflicts between hard and default information and within default in-

formation alone can arise. (For simplicity, the hard information alone is assumed

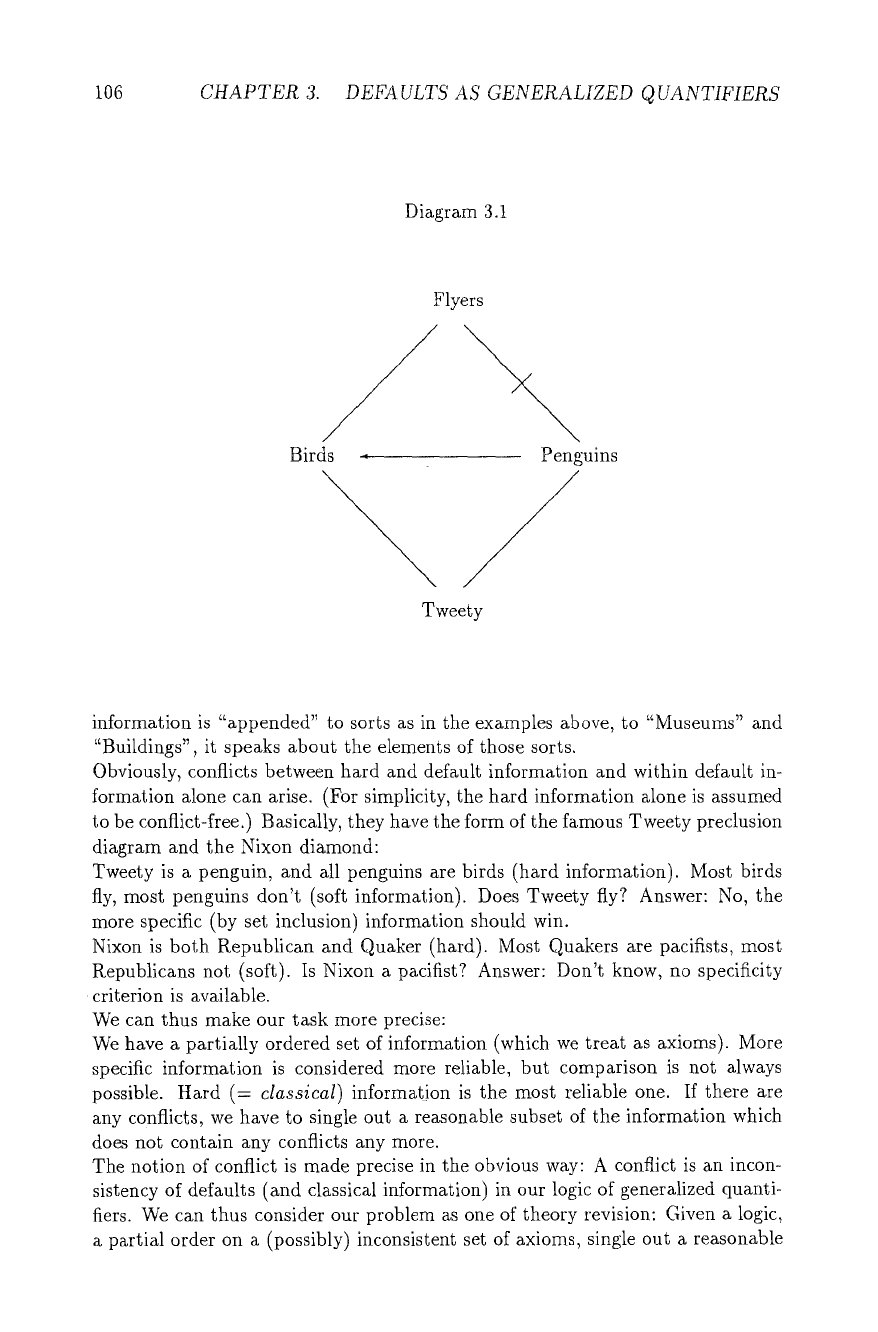
to be conflict-free.) Basically, they have the form of the famous Tweety preclusion

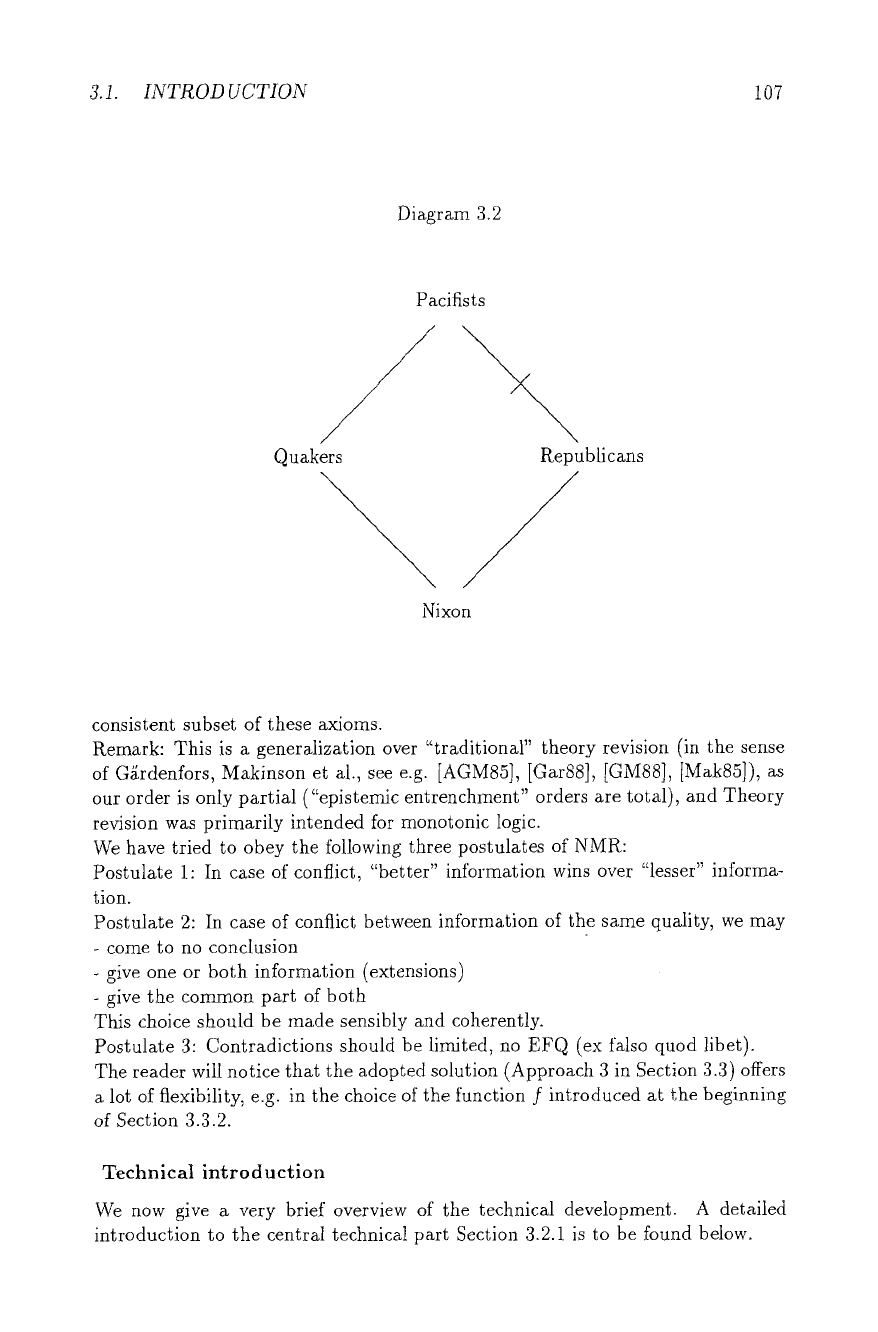
diagram and the Nixon diamond:

Tweety is a penguin, and all penguins are birds (hard information). Most birds

fly, most penguins don't (soft information). Does Tweety fly? Answer: No, the

more specific (by set inclusion) information should win.

Nixon is both Republican and Quaker (hard). Most Quakers are pacifists, most

Republicans not (soft). Is Nixon a pacifist? Answer: Don't know, no specificity

criterion is available.

We can thus make our task more precise:

We have a partially ordered set of information (which we treat as axioms). More

specific information is considered more reliable, but comparison is not always

possible. Hard (=

classical)

information is the most reliable one. If there are

any conflicts, we have to single out a reasonable subset of the information which

does not contain any conflicts any more.

The notion of conflict is made precise in the obvious way: A conflict is an incon-

sistency of defaults (and classical information) in our logic of generalized quanti-

tiers. We can thus consider our problem as one of theory revision: Given a logic,

a partial order on a (possibly) inconsistent set of axioms, single out a reasonable

3.1. INTRODUCTION

107

Diagram 3,2

Pacifists

Quakers

Republicans

Nixon

consistent subset of these axioms.

Remark: This is a generalization over "traditional" theory revision (in the sense

of Ggrdenfors, Makinson et al., see e.g. [AGM85], [GarB8], [GM88], [Mak85]), as

our order is only partial ("epistemic entrenchment" orders are total), and Theory

revision was primarily intended for monotonic logic.

We have tried to obey the following three postulates of NMR:

Postulate 1: In case of conflict, "better" information wins over "lesser" informa-

tion.

Postulate 2: In case of conflict between information of the same quality, we may

- come to no conclusion

give one or both information (extensions)

- give the common part of both

This choice should be made sensibly and coherently.

Postulate 3: Contradictions should be limited, no EFQ (ex falso quod fiber).

The reader will notice that the adopted solution (Approach 3 in Section 3.3) offers

a lot of flexibility, e.g. in the choice of the function f introduced at the beginning

of Section 3.3.2.

Technical introduction

We now give a very brief overview of the technical development. A detailed

introduction to the central techniezd part Section 3.2.] is to be found below.

108 CHAPTER 3. DEFAULTS AS GENERALIZED Q UANTIFtERS

We augment proof theory and semantics of classical FOL to deal with the (open

normal, in the sense of [ReiS0]) default "normally, ~(ac) holds". We say that

~(z) holds normally (in a model) iff there is a "large" subset of the universe of

that model in which ~b(x) "really" holds. In other words, "normally" is read as

a generalized quantifier. In that sense, our semantics is local, as we work in one

model only, and give a direct interpretation of defaults, in contrast to the various

types of preferential models (see e.g. [Boug0b], [De187], [DelS8], [tiLlVIg0], [Lif85],

[Lif86], [LM92], [McCS0], [McC86], [Sho87]) which are global, working with sev-

eral classical models. We first describe such systems of large subsets (Definition

3.1), and consider as basic semantic structures pairs 3.4 =< M,H(M) >, where

M is a model of classical FOL, and H(M) is such a system of large subsets of

(the universe of) M. Validity of Vz~(z) (= qS(z) holds normally) in 3/[ is defined

in Definition 3.5. Suitable axioms for the quantifier V are given in Definition

3.7, soundness and completeness of the axioms with respect to the semantics are

shown in Lemma 3.11 and Theorem 3.12 there. The system permits full nested-

hess and boolean combinations of defaults. In particular, a notion of consistency

of defaults results. The rest of Section 3.2.1 is devoted to extensions of the basic

idea: (Open normal) defaults with prerequisites are seen as restricted generalized

quantifiers, defaults of various strengths of "normality" are introduced, sound-

ness and completeness shown. In conclusion, we examine various strengthenings

of the axioms, which correspond to widespread use of defaults and other systems

of defensible reasoning discussed in the literature.

In Section 3.3, we use the notion of consistency of defaults given in Section

3.2.1 to choose a reasonable consistent subset from a possibly inconsistent set

of default information. We exploit the reliability relation given by the (partiM)

order of specificity in the sorted language of the LILOG project. The basic idea

is to consider minimal inconsistent subsets, and to eliminate at least one suitably

chosen (according to specificity, and determined by the function f there) element

from each. Several approaches are discussed, one of which has essentially been

implemented.

3.2 Defaults as generalized quantifiers

Overview for this Section

In this Section, we first take up the informal discussion of the introduction in

somewhat more formal terms. Moreover, we also present several problems with

the common use of defaults. We then proceed to the formal part of rigorous

definitions, theorems and proofs.

The common use of defaults seems to presuppose strong assumptions on the

structure of the universe - and seems thus to have common aspects with learning,

and even philosophy of science. E.g. applying both defaults "normally ~(z)" and

"normally ~b(x)" seems to presuppose that not only "normally aS(x)" and "nor-

mally ~b(x)," but also "normally q~(x)A~b(z)." Even if our base system is too weak

so permit such reasoning, we can easily adapt it by introducing a corresponding

3.2. DEFAULTS AS GENERALIZED QUANTIFIERS

109

axiom schema, and strengthening the system of 'qmportant" subsets to a filter.

Problems of this kind are discussed in the Introduction, Section 1.3.11.

Section 3.2.1 contains the central definitions and results of this Chapter. We

introduce N-systems, which formalize the notion of a "large" or "important"

subset, introduce the generaIized quantifier V - read e.g. "for almost all". N'-

systems then provide us with a semantics: A V-structure (or -model) is a classical

first-order structure with an N'-systern over its universe, and a formula Vxr

is defined to hold in an V-structure iff there is a large subset A of the universe,

i.e. some A in the N-system over the universe, such that for all elements a E A

r holds. An axiomatisation is given, soundness and completeness for our

semantics is shown. (For simplicity, we first treat the case of normal open defaults

without prerequisites - corresponding to Vxr in our notation - the extensions

to those with prerequisites is straightforward: Vxr : r is interpreted as a

generalized quantifier restricted to {z: r

The weakness - choosing N-systems weaker than filters, and making no but trivial

connections between the N-systems over different subsets of the universe for

the relativized V-quantifier - is deliberate: We make as little '~philosophical"

commitments as possible, and permit easy and straightforward strengthenings

into many different directions. In particular, the axiom systems P and R of

[KLMg0] and [LM92] can be incorporated easily into our system. Several such

extensions are discussed in Section 3.2.2.

3.2.1 Semantics and proof

theory

Overview for this Section

The basic definition of the Chapter is that of an N-system (over a set M), it

is given at the beginning of this section. We recollect that an H-system over

M is supposed to capture the notion of a "large" or "important" subset, or

one containing the "important" or "typical" elements of a base set M. Let me

emphasize again that we have made the properties of an .M-system deliberately

extremely weak, weaker than a filter. Thus, our approach is generic on the

sense that, if need be, we can strengthen the notion of an H-system, add the

corresponding axioms to the proof theory and still have a sound and complete

system. Such modifications would be harder to achieve if, instead, we had to take

away some undesirable strong properties.

The axioms for an H-system of large subsets over M are:

(1) M is large,

(2) supersets of large subsets are large,

(3) the intersection of two large subsets is non-empty.

The first property could be replaced by making the system itsetf non-empty.

The third property is the most interesting one. A filter would require the intersec-

tion of two large subsets to be large itself, we content ourselves with non-empty

intersection. This permits e.g. a simple probabilistic interpretation by "more

than half". It is property (3) which permits - in the intended interpretation - to

110 CHAPTER a. DEFAULTS AS GENERALIZED QUANTIFIERS

deduce that ~'normally qh(z)" and ~*normally -~5(z)" together can't be: there is

no element which satisfies both ~(z) and -,~(z).

The further development proceeds in two stages. We first treat normal open

defaults without prerequisites, and then extend the discussion to normal open

defaults with prerequisites (and N'-families, see below). All essential techniques

and ideas are present in the case without prerequisite, and the reader so inclined

may just leaf through the later subsections.

We introduce the new (unbounded) quantifier V into the language (and its dual

& for proof theoretical purposes only). The crucial definition linking language

and semantics is Definition 3.5, where we define an N'-model and validity of a

V-formula in an additional inductive step: An N'-model is a classical first-order

structure, with an N'-system of large subsets over its universe M. Vz~b(x) is

defined to hold in the N'-model, iff there is a large subset A C_ M such that

for all a E A •(a) "really" holds. As 4~ was not necessarily a classical formula,

we can treat nested V's. Moreover, the new quantifier is fully embedded into

the classical setting, so we can form boolean combinations, quantify classically

over defaults in the sense of e.g. 3zVy&(z,y) etc., and give these formulas a

precise meaning, preserving the constructive spirit of FOL. This seems to me one

advantage over "global" Kripke style semantics where we have to ~look elsewhere"

for the interpretation of normality. Here, we can say ~%ok, you see its holds in

this universe on a large subset, so it normally holds here".

A corresponding axiomatisation follows in Definition 3.7: The first axiom says

that implication preserves normality: If q~(z) normally holds, and qh(z) implies

~b(z), then ~b(x) normally holds. This corresponds to the second property of N'-

systems. The second axiom says that normally q5 and normally -~b can't be (we

have discussed this above), and the third that the V-quantifier ties between the

two classical ones, corresponding to the fact that M is a large subset of itself.

(The second half of the axiom could be derived by -~?a:~b(z) + gx-,~(z) --+

Vx-~r --~ -~Vxr - we prefer to state it explicitely.) The last two axioms

are auxiliary.

Lemma 3.8 states some basic and trivial consequences of the axioms. We then

give a normal form for V-formulas to facilitate the completeness proof.

The central result of the Chapter is given in Lemma 3.11: A consistent V-theory

has a model. The idea is to consider first-order consequences of pairs of V-

formulas: Assume T to be deductively closed under our axiomatisation. Let

Vxr Vy~b/(y) E T with, for simplicity, ~b, ~bl classical formulas. By Lemma

3.8, a) Vzg~(x) A V~J~b/(y) --+ Bx(~b A ~b~)(x). We now take a classical structure

M satisfying all those first-order consequences, say M ~ ~b A ~b1(cv,^~,, ). For fixed

Vx~b(z) E T, let Xv~(~) := {c~^v,, : Vz~r E T}. Xwv,(~) will be one of

the large subsets of the system to be constructed. It remains to show that the

intersections of those sets are non-empty, and that the defined structure really is

a model of T, But this is not difficult.

The soundness and completeness theorem is a direct consequence of this Lemma.

The extension to normal open defaults with prerequisites is straightforward:

Vzr : ~(z) (r ~b(a:), then normally ~p(x)") is interpreted as a generalized

3.2. DEFAULTS AS GENERALIZED Q UANTIFIERS 111

quantifier relativized to {z : ~(z)}, i.e. we consider an .M-system not over the

whole universe, but only over the subset where ~fi(z) holds. Again, we keep our

system deliberately very weak, in the sense that we do not demand any con-

nections between the H-systems over the different {z : ~(z)} and {z : ~,(z)}

besides the trivial ones when e.g. {z : ~(z)} = {x : ~b/(z)}. We even do not

postulate A E A/'(B) A A C_ BI _C B --* A E Af(BI), which a purely quantita-

tive reading would justify: A large subset of B is afortiori large in BI, when

A C_ BI C B. Again, we want to leave open all possibly intended developments

and strengthenings.

The next extension concerns different degrees of normality. This is again straight-

forward and the reader is referred directly to this subsection.

Semantics

Definition 3.1 Call A/'(M) C P(M) (= the powerset of M) a H-system over M

iff

a. M E .M(M),

b. A E N'(M), A C B _C M ---, B E H(M),

c. A, B E N'(M) --+ A M B ~ 0 if M ~ 0 (thus, {~ ~ A/'(M), if M ~ 0).

(Note that this is weaker than the corresponding axiom for filters.)

To facilitate proofs and enable normal forms, we introduce a complementary

quantifier, &, too, with the meaning ,$x~(x) :~-+ -~Vz~q~(z). The intuitive reading

of &zr is thus roughly: "for at least a few z, 4(z) holds".

Remark: Our semantics covers the two extremes:

fix one element a of the universe U, then {A C_ U: a E A} will be a X-system

let some probability measure be given on U, then {A C_ U: p(A) > 0.5} will be

a H-system.

(Note, however, that the former can also be expressed by a suitable point measure

on U.) We can thus cover both the "prototypical" and the "average" case.

Remark 3.2 a) Af stands for normal. We formalize "~fi is normally valid in e"

by ~a E A/'(c).Vz E a.r

b) There is nothing to prevent e.g. Af(c) = {a C c : :c ~ a} for some fixed

z E c. This might seem pathological. Two comments: First, compare to topology.

Suitable choice of topology will make e.g. the function d : N + N,

0 iffz is rational

d(z) := 1 otherwise

continous, certainly a pathological case too. Second, this z might be a very

prototypical case, and thus have ifltuitive meaning.

Lemma 3.3 Let f. C_ P(X) be such that A, B E f. ~ ANB # ~. Then N'(X) :=

{A _C X: 3/? ~ s C A} U {X} is a N'-system over X. []

Example 3.1 Let o be any ordinal, and U := {f:c~ ~ 2 = {0, 1}}. For i < c~

let Xi := {f E U : f(i) = 1}, X,,~ := {f E U : f(i) = 0} = U-Xi. For j < a

112

CHAPTER 3. DEFAULTS AS GENERALIZED QUANTIFIE'RS

let Ij C c~, Itlj C c~ -- {j} such that

Ij ,q DIj

= ~, and let s :=

{Xj N X~ : i

Ij} U {Xj N X~ : i ~ Dr

Then Kj satisfies the prerequisites of Lemma 3.3 for

Xj and all j. Consequently, Kj so defined generates a H-system over Xj for all

j~oz,

Proof

s C W(Xj)

is trivial. As Ii A I/1j = 0 and j ~ Ittj, the function

1 ifi=joriEIj

f(i) := 0

otherwise

is well-defined and in all

Xj C3 Xi, Xj n Xlli. []

Definition 3.4 We augment the language of first-order logic by the new quan-

riflers: If r and 0 are formulas, then so are Vzr

&xS(x),

Vxr :

"O(x),

&xr : r for any variable x. We cdll any formula of s possibly containing

V or & a V - K-formula.

Definition 3.5 (JV-Model)

Let s be a first-order language, and M be a s Let H(M) be a N-

system over M. Define <

M,N'(M)

> ~ r for any V - K-formula inductively as

usual, with two additional induction steps:

< M,H(M)

> ~ Vxr iff there is

A E H(M)

such that Va E A (<

My(M) > ~ 4[a]),

< M,N'(M)

> ~ &x4(x ) iff {a E M: <

M,A/'(M)

> ~ -~r r N'(M).

Lemma 3.6 <

M,N'(M)

> ~ &xr

eH(M)3a E

A(<

M,H(M) >~

r []

Proof theory

Definition

3.7 Let

any axiomatization of predicate calculus be given. Augment

this with the axiom schemata

1. We(x) A W(r --* ~(z)) =, W0(z),

S. Vxr --, Vxr ~ ~xr

5. Vxr +-+

Vy4(y) if x does not occur free in qS(y) and y does not occur free

i~ r

(for all 4, 0)-

We also denote the corresponding notion of derivability by Fv.

Lemma 3.8 The following formulae are derivable:

a. We(x) A Vx~(z) --* 3x(r A r

b. v~r A -,W~(~) ~ 3~(r a-,r

c. ~W-,r --+ ?xr

d. &xr --, 3me(x),

e. we(.) i ~,x~(.) + 3~(r A

~)(~),

f. Vx(r ~ '0(~)) -~ (Wd(~) ~ W-~(x)) /x (,~.r ~ ,~(~)),

g. Wr + ~,.r

3.2. DEFAULTS AS GENERALIZED QUANTIFIERS 113

It is usually r~ot derivable: &zo(z) A &z~(z) ~ ~'(~ A '~)(z). (To see this, use

Theorem 3.12 below and argue semantically.) []

Soundness and completeness

To prepare the proof of completeness, we introduce V-normal forms (V-NF).

Definition 3.9 ~b is in V-normal form (V-NF) iff

1. q~ contains only -7, A, V as propositional operators,

2. only atomic FOL formulas are in the scope of -~.

Lemma 3.10 For every ~b there is q~1 in V-NF such that ~-v ~b ~ ~bt.

Proof B2~ induction on the depth of V + & - nesting.

Lemma 3.11 Let T be a V - s Then T is consistent under the axioms

of Definition 3.7 iff T has a model as defined in Definition 3.5.

Proof The consistency of T when it has a model is trivial.

Let T be a t-v-consistent V - s We have to show that it has a model.

Throughout the proof, let "t-v-consistent" be abbreviated by "consistent". We

give a constructive proof, to make the reader comtbrtable with the new logic. By

the above, assume without loss of generality that all ~b E T are in V-NF.

We first construct a consistent Tr D T.

We add % : a < n new constants to s where n is the size of s and inductively

construct TI = I J{T-y : 3' < 8} (T~ ascending, fl large enough) with To := T, by

adding new tbrmulas to T, preserving consistency. (For simplicity, we omit the

exact enumeration process - it does not matter anyway.) Let ~b E T~, depending

on the topmost operator, we add 0, 1, or several new formulas. It should be noted

that all added formulas are in V-NF too.

Case 1: 4; = ~: We do nothing, by V-NF, ,~ is a classical atomic formula.

Case 2: q~ = ~p A ~/: We add zp, ~bl, obviously preserving consistency.

Case 3: ~b = ~ V ~p1: Both T-y + ~p and T~ + ~pl can't be inconsistent, as q~ E T-y, so

add one (or both) which preserves consistency.

Case 4: r = Vxr Add all ~p(c~), c~ < K.

Case 5: r = 3zr Add some r which preserves consistency.

Case 6: ~b = Vz~b(z): Add ?zr and tot each Vyr E T~ ~z(~, A Ct)(z)

and for each &yr E T~ Jx(r A r (after suitable renaming, preserving

consistency by Lemma 3.8).

Case 7: q~ = &xr Add 3xr and for each Vyr E T, ?z('~ A r

(after suitable renaming, preserving consistency by Lemma 3.8)

In case 6 and 7, we mark all new 3xr / 3z('~Ar as children of ~b = Vx~p(x)

/ r = w~{~) and r = W,~(~:) etc.