Schlechta K. Nonmonotonic Logics: Basic Concepts, Results, and Techniques

4.2. TECHNICAL DEVELOPMENT

135

as the initial segments S give a uniform distance measure. In particular, we can

define uniform continuity of a function between two such topological spaces and

show that any continuous function on a compact space is uniformly continuous.

(This is discussed in the material from Example 4.2 to Lemma 4.12.)

The subsequent material up to Corollary 4.17 carries the construction over to

logics, to theories more precisely. X is now presumed to be the set of propositional

variables of some language K, ordered by importance, the most important ones

the smallest. If S C X is an initial segment, T an K-theory, then

Us(T),

the

S-neighbourhood of T, consists of all theories TI such that

M(TI) E Us(M(T)),

where

M(T)

denotes the set of models of T etc. We can transform T into a

classically equivalent theory

T d,

consisting of all classical consequences of T which

are pure disjunctions of literals.

Td[[S

will be the subset of T e consisting of

all such r E T ~ in which only propositional variables from S occur. We have

TIE Us(T)iff

Tells = TI~[[S, moreover

T~[[S E Us(T),

and

Tells

is themost

general S-neighbour of T, i.e. TIE

Us(T)

implies

TI [- Td[[$.

Fact 4.18 shows compactness of the theory space in a special case, and Lemma

4.19 - Example 4.4 discuss continuity of logics on our theory spaces and the

relation between continuity and compactness (as a logic). The hurried reader

may skip this part too.

In the last Section, we define a a-algebra A on

Th~ (K

countable), and a measure

# : A ~ N. To this end, we construct a sequence of partitions of

ThL.

We start

with the trivial partition Rio :=

{ThL}. For ~

< ~,

we

set R/,~ :=

{Th(Gfn)

:=

{r: M(T) ~ U~(G)} : a c 2v(L/}. It is

easily seen

that this is a successive

refine-

ment: If n/> n and

Th(G[n) N

rh(Gl[nl) r 9, then

Th(GIfnl) C_

Th(G[n). We

assign each

Th(G

In) inductively an interval on the real line

g(Th(G

In)), starting

with

g(rhL)

:= [0,1),

and,

if

g(Th(G[n)) = [x, zl),

we give each

Th(G1[n +

1)

with

rh(Gr +

1) C Th(G[n) an equal share [y, y/) C Ix, xl). The size of [x,x')

determines that of

Th(G[~), i.e. p(Th(a[~)) := zl

- ~, if we start with the

standard measure on ~. The definition extends naturally to the a-algebra ~4

generated by I.J{Rr : n < w}, defining a measure on al. For two theories T,

Tt, we set their difference

T~TI

= 0 iff T = T/. Otherwise, there will be a

least n such that

M(T)[n r M(TI)[n,

and

TATI

will be set ~. Given two

logics I~, I~ l, we can then define their difference function [~-, A I~ I by

~.0 A ]~ I)(T):= ~--, (T))A@. I(T)) E N. We conclude by showing that, ifl~

andl~ / are continuous with respect to our standard topology, then f@. /k l" I),

i.e. their average difference, is defined. We use here the fact that all open sets of

the topology are in the a-algebra A.

4.2.2 The topological construction

Definition 4.1 Let X be a set, partially ordered by < . If X is an ordinal, _< is

the natural order, unless said otherwise.

S C_ X is called an initial segment of X, iff

x E S, x! E X, x/<_ x

implies xl E S

(i.e. S is downward closed). To avoid pathological cases, we assume S r ~ in

the sequel - though we will not be very exact about this point, it really does

136 CHAPTER 4. LOGIC AND ANALYSIS

not matter. Let E C_ 79(X) be a set of initial segments of X, totally ordered by

set-inclusion.

Let D be a set, F := D x = the set of functions f : X -+ D. For G _C F, S C X,

let G[S := {f[S : f E G}. Let Y C'P(F) be fixed. For G E )v, S C_ X, let

Us(G) := {H E ~: G[S = H[S}. Given F as above, S~ will denote the set of its

singletons: 5v~ := {{f} : ]'E F}.

If < I is a maybe different partial order on X, E/ a set of < l-initial segments of

X totally ordered by set inclusion, we say E y E/(E is finer than El) iff for all

Sl EEI there is S 6 E such that St C S.

Fact 4.2 Let G, Gl C_ F, SI C_ S C_ X, OrS C Gl[S, then G[SI g Gl[Sa

We obtain the basic

Lemma 4.a

i)

Let G, G, C 5", S/C S C X, Us(G) ~q Us,(GJ r {~, then Us(G) G

2) In particular,

Us(G) r] Us(G') r ~ *-+ Us(G) = Us(GO ~ G[S = Gt[S

a, us(a)

(for G, ol

3) Let G 6 ~-, SIC S C X, then Us,(G) = U{Us(H): H E 2, G[SI = HISs}.

4) Let D be finite, G C_ D x, S C_ X, z C X - S, G IS be finite, and K :=

{H[(S U {x}): H C D x, HIS = G[S}, then card(K) = card(2 v - 1) ~g(Ccs).

Fact 4.4 1) G[S=~ ~ G=O,

3)

o

r --, r Us(a) for all

s.

Corollary 4.5 Let 5", <, E, G I, El be as above, then

1) {Us(G): G G ~-, S E E} is the basis for a topology T = Tz on 2 c,

2) each Us(G)is cIopen (= dosed + open)in T,

a) let S E E, 7-f c 2, then U := U{Us(H): H C ?-f} is clopen,

4) if E -'4 Ef then T~, C_ Te.

4) shows that, to a certain extent, the order does not matter. What matters here

is, how far we approximate X from below. In particular, if E _ El y E, then any

function continuous with respect to Tz will be continuous with respect to Tz, too.

An even stronger independence result is given in Lemma 4.12, 2) where we show

that such E, EI do not change the uniformity of continuous functions. (Of course,

this does not always hold when the topology stays the same, as manipulating the

usual metric by e.g. ! shows.)

This-may be the place to indicate a possible (and straightforward) extension to

the predicate logic case:

For reasons of homogenity, we work on a fixed "superuniverse" W, which we take

large enough - a class, if you don't like to use downward L6wenheim/Skolem. Our

real universes will be subsets of I/V. More precisely: Let s be a first order language,

T an s We add a new unary universe predicate U to/J and relativize all

r ~ T to U, i.e. for each constant c, we add U(c), functions and predicates will be

4.2. TECHNfCAL DEVELOPMENT

t37

restricted to U, quantifiers too, i.e. Vzr will be replaced by gx(U(x) --~ r

3xr by

3x(U(x)

A r Without loss of generality, we now assume that s

has only predicate symbols. As in the propositional case, we assume an order

< to be given on the predicates - including U - which determines the degree to

which models differ. For simplicity, assume them to be totally ordered and finite

in number: p0 < pt < ..-pr~. We can now say that two/;-structures m and rnf

have distance i, iff

po...pi

have the same extension in rn and rn 6 but Pi+l is

interpreted differently in m and rnL Note that our treatment of the universe as

a new predicate allows us to attribute arbitrary importance to the preservation

of the universe - depending on where we place U in our order. Obviously, this

development is totally in parallel to the propositional case. We may, of course,

add refinement by considering also the size of the area on which the predicates

differ (by cardinality or subset-relation). The difference of two theories is then

again determined by the difference of the sets of their models.

Corollary 4.5, 2) has strong consequences for separation properties:

Lemma

4.6 1) T

satisfies Ta and

T4,

2) if T satisfies To, then it satisfies T~, so To, T1, T~ coincide for T.

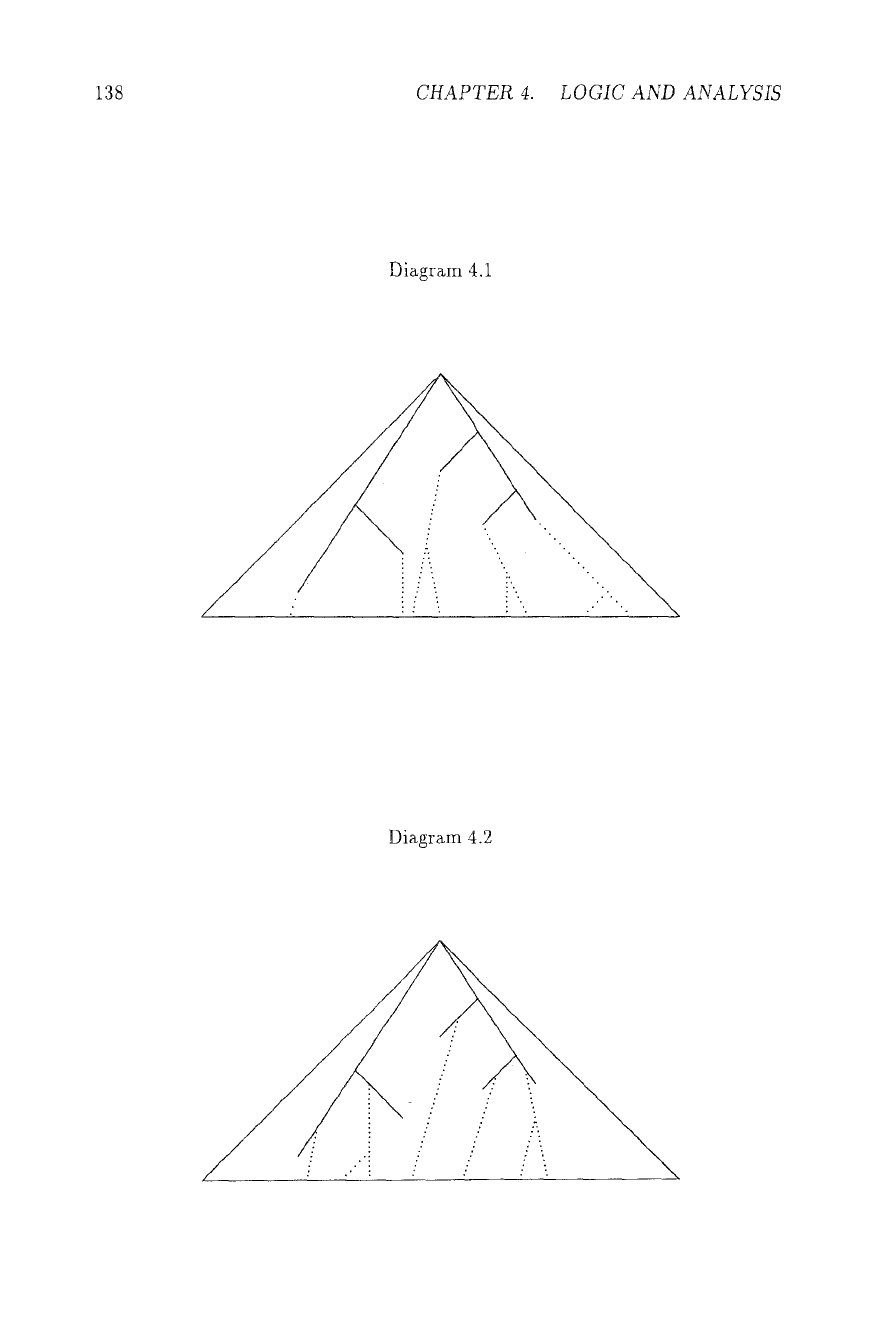
For the intuition, the reader is referred to Diagrams 4.1 and 4.2. A base set

Us(G)

can be identified with

G[S,

so any open set with

Gi [S;, i E I.

We can add a root

and consider -?-1 (for simplicity) as a tree T of branching factor card(D). So

G[S

is a - usually non-cofinal - branch in T, shown by full lines in Diagram 4.1. The

open set

U{Us,(Gi): i C I}

consists of all continuations of some

G~[SI,

speaking

"botanically", of all end-growths trom some

Gi [Si -

dotted lines in Diagram 4.1.

The elements of the complement, i.e. of a closed set, are "side-growths" of the

Gi [Si - shown by dotted lines in Diagram 4.2, they are not continuations of any

a~

[Si.

Definition 4.7

i)

E is called cofina!, iff U E = X,

2) E is called 5-cofinal, iff for all

G, GI E S, G r GI

there is S C E such that

ors

r a, rs.

It is not true that E cofinal -4 E 5-cofinal for all .T, as the following example

shows (see, however, Lemma 4.!3 below for D).

Example 4.1 Let X = E = w, D = 2 - recall that any ordinal is the set of

its predecessors - (note also that we are slightly inexact here, as 0 E E, and we

assumed above that nil S r 0, but this is not important, so we just neglect it).

Obviously, E is cofinal. For n E w + 1 let f~ : aJ -4 2 be defined by

f,(m)

= 0 iff

rn < n. Let G := {fn: n < w}, G/:= {fn : n < w}, .T := {G, GI}. Then, for each

S=nCw=E,f~[S=f~[S, andthusforeachSEEG[S=Gl[S. [3

Lemma 4.8 1) ~ is .T-cofinal iff 7- is T2,

2) if ~ is y-cofinal, a ~ 7, then P,{U~4G): S ~ ~,} = {C}.

138 CHAPTER 4. LOGIC AND ANALYSIS

Diagram

4.1

Diagram 4.2

4.2. TECHNICAL DEVELOPMENT

139

It is easy to find non-compact examples, e.g. by making D infinite, or by. taking

E = X = w + 1, D = 2, and considering ~- := Yl. The following positive result is

a little more interesting:

Definition 4.9 5 r has the E-intersection property iff for all U =

{Us;(G;) : i E

I} (S~ E E, G~ E ~), totally ordered by set-inclusion, I"l U # ~.

Lernrna4.10 Let D finite, E = X = co, 5 r _C

P(D x)

such that Y has E-

intersection property, then T is compact.

Proof Suppose not, so there is W :=

{Us,(G;) : i E I}, & E E, G; E 5

with

U W = ~', but for no finite I0 C_ I we have

U{Us,(G;) : i E

I0} = 5 v. Define a tree

on T := {<

Us(G), S

>:

S E E, G E .~, VSI < S.Us,(G) r W}

by <

Us,(G), Sl >

< < Us(H),

S > iff

St < S

and

Us(H) c_ Us,(G). < Us(G), S >E T

has height

SinT:

To demonstrate this, we show that {<

Us,(G),SI

>: St < S} are exactly the

predecessors of <

Us(G),S

> . First, for S/ < S <

Us,(G),SI

>E T : As

< Us(G), S >E T,

for all

Sll < S Us,,(G) ~ W,

so a fortiori by SI < S for all

SII < St Us,,(G) f[ W.

Second, obviously <

Us,(G), St > < < Us(G),

S > . On

the other hand, if <

Us,(H), SI > < < Us(G),

S >, then by definition $f < S

and

Us(G) C_ Us,(H),

so

G E Us,(H),

but then

Us,(H) = Us,(G).

Note that for each S E E

{Us(G)

: G E $'} is finite, as D and S are, so

there are only finitely many G IS. Thus, each level of T - which is of the form

{<

Us(G), S

>: G E 5-} - is finite. But T has also elements of arbitrary height.

< w: Suppose not. Then there would be S, such that for all G there is

SI < S

and

G E Us,(G) E W,

giving a finite subcover of W.

By KSnig's Infinity Lemma, T has an infinite branch B = {<

Usj(Gj), Sj

>: j E

co}, and by E-intersection property, there is

G E f-l{Us,(G d)

:<

Us,(Gj),Sj >E

B}. But G r UW : Suppose

G E Usk(Gk) E W

for some k E [, then Sk = S~ for

some

j E w, G E Uso(Gk) M Us,(Gj),

and

Usk(Gk) = Us~(Gj) ~_ W

(by Lemma

4.3, 2)), contradiction. []

If any topological space (.~', T) is a metric space, defined, say by a metric p, then

{Ur(x) : z E S,r > 0} with

UT(x)

:= {g :

p(x,y)

< r} forms a basis, so for all

x E S there is a countable set {U~(x) : n < co} of open neighbourhoods of x

dense in the neighbourhood filter of z, i.e. if U(x) is a neighbourhood of z, then

there is n < co such that

U• C U(x).

Thus the following example is not a metric space:

Example 4.2 LetX= E=col, D =2,$v=)v G= {f} ES. Obviously, for

C

$1 < S < wl Us(a) y~ Us,(G).

Suppose there is a countable set

U~(G) : i < co

dense in the neighbourhood filter V(G), so it is in particular dense in

{Us(G) :

S < COl}, and as each

Ui(G)

contains some

Ux~(G),

Si < COl, there is a dense

set

{Us~(G)

: i < co}. But, by regularity of col,

sup{Si

: i < w} ~ c~ < COl, so

C

U~+I(G) r

Us~(G)

for all i < co. Contradiction. []

140 CHAPTER 4. LOGIC AND ANALYSIS

Usually, ~'uniform continuity" or %niform approximation" are defined for metric

spaces only, but one does not really need all properties of a metric to make

such definitions. The uniformity of the construction of the Us(G) allows us to

speak about uniform continuity (and approximation): all we really need is for all

G E ~" a dense subset V'(G) of the neighbourhood filter such that all V'(G) are

comparable. But, of course, the systems {Us(G) : S E I3}, being a basis of the

open sets, provide such dense sets. In particular, we define and obtain:

Definition 4.11 Let T be defined on ~-, TI on $I as above, f : ~- -+ Y't is

called uniformly continuous for the spaces (~,7-), (Sc1, T/) iff VS/ E E/3S E

EVG E Y.f[Us(G)] c__ Us,(f(a)).

We shall also use the

shorthand notation f :

(~c, 2/-) --~ (~'/, T/) to fix the topologies concerned.

Simple continuity is, of course, defined as usual, i.e. by f-l[Ul] E T for all

UI E Tt, or, equivalently, by VS! E E/VG E )v3S E E.f[Us(G)] C_ Us,(f(G)).

Lernma 4.12 1) Let f : ()v 2r) -, (9v6 Tt) be continuous, T compact, then f

is uniformly continuous.

2) If2 -+ is constructed from E +, 7 -~ from E ~, T from E, T' from P/, i.e. T + = T~+

etc. in the notation of Corollary 4.5, and E+ J E, El -4_ E', and f : (~',T)

(SvI, TI) is uniformly continuous, then so is f : (~,T +) ~ (SrI, T*).

We turn to logics

Let X be the set of propositional variables for some propositional language t2. (We

sometimes identify propositional variables with their indices to simplify notation.)

Then any (classical) model ra is equivalent to a function f~ : X --* 2, so we can

identify m and f~. Not all sets of models correspond to theories, so we consider

only D C 72(2x). Moreover, ra (or f~) shall also denote the set of literals which

hold in ra, and for Y C X, m IY or f~ IY will also denote those which hold in ra

and are in Y. T etc. shall denote a E-theory, i.e. T E Thz.

Lemma 4.13 If E is cofinal, then it is D-cofinal.

Proof Suppose not, so there is A, Af E D, A r At, but for all S E E A[S =

AI[S. Let A = M(T) (i.e. A is the set of modeis of the theory T), At = M(TI),

and m E A!-A (the case ra E A-A/ is symmetrical). Thus, by our above

assumption, for all S E E, there is 'ms E A such that m[S = ms[S. As ra ~ T,

l~here is .6 E T such that m ~ 7.6, but, by the inductive definition of models and

finiteness of 6 (or by compactness of classical iogic), there is Xo C C_ X finite such

that m [Xo determines .6. As E is cofinal and X0 finite, there is S E E such that

Xo C_ S, so rags determines -,.6. But, as ra[S = ras[S, ras ~ -'4, so ras ~ T,

and 'ms ~d A. Contradiction. []

Definition 4.14

I) A

formula

r

will be said to be in strictly disjunctive form iff

it is of the form _~Pi0 V .,. V q_:2~, with p~ propositional variables. A theory T is

said to be in strictly disjunctive form, iff all .6 E T are.

4.2. TECHNICAL DEVELOPMENT

141

2) Recall that T denotes the classical closure of T, and let T d := {r E T : r

is in strictly disjunctive form }. Obviously, T and

T e

are classically equivalent.

(T would do, but

T e

gives the intuitively dearer picture.) 3) Let Y C_ X, then

T[[Y

:= {r E T: in r occur only propositional variables from Y}.

Note that for any model rn, rn[S decides all r E

T[[S.

We have:

Fact 4.15 1)

m[S 9

M(T)[S ~

Con(T,m[S).

2)

Td[[S C_ T#[[S *--* M(Td[[S)[S D M(T#[[S)[S,

3)

M(T d

[IS)IS =

M(T)IS,

thus

T d

[IS =

T, d [IS ~

M(T)IS = M(T,')IS,

4)

M(Td[[S)

= {rn :

rn[S E M(T)[S},

so, beyond

S, M(Td[[S)

can take any

value.

Definition 4.16 We abuse notation and define

Us(T)

:= {Tl E

Thr_. : M(TI) 9 Us(M(T))}

= {TI:

M(Tf)[S = M(T)[S}.

For G C 2 x, S C_ X, let

Th(GVS )

:= {T E

ThL: M(T)[S = G[S} -= {T 9 Thz.:

M(T) E Us(G)}.

(Thus, for

T E Th(G[S), Th(G[S) = Us(T),

in particular

Th(M(T)

IS) =

Us(T).)

Corollary 4.17 1)

Td[[S = TId[[S ~

(by Fact 4.15, 3)) M(T)[S = M(TI)[S

M(TI) E Us(M(T)) ~ Tf E Us(T),

2)

Td[[S

is the most general S-neighbour of T,

3) a logic f, which we also write in the more "logical" notation =, is continuous

iff w~ ~ rVT3S 9 ~VT~(T~

~ Us(T) -+ T~ 9 Us,(~)),

4) if G, Gt C F = 2 x, S C_ X and

G[S r Gt[S,

then

Th(G[S) ~ Th(Gt[S) = ~,

5) let S _C St, G C F, then

Th(G[S) = ~{Th(H[SO: H C_ F,H[S = G[S},

6) if E is cofinM, then {T} = ~{Th(M(T)IS): S E E} (up to logical equivalence),

7) if S is finite, then

Th(a[S) r 0

for any G _ F,

8) thus, by 4) and 7), for finite S, there is a one-one correspondence {G[S: G C

F} ~ {Th(GfS) :

G c_

F} such that

G[S 7~ GelS ~ Th(G[S) M Th(G,[S) = O.

Fact 4.18 D has the E-intersection property for all E, so in particular, 7- is

compact for E = X = w.

Proof Let U :=

{Us~(Gi) : i E I} -

without loss of generality without rep-

etitions - totally ordered by set inclusion, and define < on I by i < j :~

Us~(G~) C Usj(Gj).

Let Ti be such that G~ = M(T~). We have

i < j ~ Sj C_ Si

and

T~[[Sj = TS[[S j.

Consider now T := U{(T/[[SI) : i 9 i}, we show

M(T) E A U.

By Corollary 4.17,

1)

M(T) E Us~(Gi) ~ Td[[Si = T~e[[$i,

so we have to show the latter for all

i 9 I. Obviously,

T•[[SI C

Td[[S~. Let now r 9

T~f[N,

so there is finite/0 C I,

and Cj E

T~[[Sj,

A{r : J E -To} b- r Let k :=

min(Io)

(by above order on I).

For j Zo, k < j, so + TJ[rS = T .CCS c T CCS , so all 9 T2CrS c ,

so r ~ ~[[x~. Case l: i <__ ~. Then T~[[Sk = r~[[s so ~11

Cj ~

r~[[s c_ r~,

so T rrs Case 2: < i.

Then

r

E

r:rrs

-- T rrs . []

Lemma 4.19 Let X = E = w, f (written also 1~ or =) a continuous logic on

X, then f is compact as a logic.

142

CHAPTER 4. LOGIC AND ANALYSIS

Proof Let T]~ r r E TI :=T, we have to find To C T finite such that

T01~ r As r is finite, there is St E E such that for any model m, already m [St

decides r thus for T, G

Us,(Tf), T, ~ r

By continuity, there is S such that

flUs(T)] C_ Us,(Tl).

In particular,

J(Td[[S) E Us,(TI),

so

Td[[S I~ r

but we

have to do a little more. By finiteness of S, Tells is equivalent to a finite set

of formulas, so there is some finite To C T such that

To t- Td[[S.

It remains to

show To]'-"

4.

But

T F

To [-

rd[[ S,

so

T~[[ S D Tod[[ S D_ (Td[[ S)d[[ S = Td[[ S,

so To E

Us(T)

by Corollary 4.17, so ToI~ r []

But not vice versa:

Example 4.3 A logic which is compact, but not continuous:

LetX=E=co.

Define

=T :: ( TI; (i.e. all s otherwiseiff T t- -~pi for some i < co

k

1~ is compact: Let T[~ r ifT t- -~p~ for some i < co, then there is To C_ T finite

such that To I- ~pi, then To I ~ r If

T ~/-'pi

for any i < co, then T F- r By the

welt-known compactness of classicaI logic, there is finite To C_ T such that To ~- r

so also To 1~ r by definition.

t~ is not continuous: Consider To := {p; : i < co), then To = To, and let

Sl E E be given, then s r

Us,(~)

(As M(s = (~, but M(Too) not). On the

other hand, for any S E E, there is TIE

Us(To)

such that TI = s just take

T~ := {p~ : i < S} U {-~p; : S _< i < co}, giving a direct contradiction to the

definition of continuity. []

Example 4.4 A logic which is continuous, but not uniformly continuous:

Let E = X = co +co.

Define

Z :=

T +p~ iff there is m E w such that m = {n E ~ : T t- p~} and T b p~+~

T otherwise

IN is continuous:

We examine the different cases for T.

Case 1: {n E w : T F p~} r co. Then T = T. Let $/ E E be given, consider

S :=

max{co, Sl}.

Let Tt E

Us(T).

Then {n E co : Tr ~- p~} r co, so T/=

Tt.

We

have to show T~ E

Us,(T),

but Tr E

Us(T)

~ T-~ = T/E Ds(T) =

Us(~) G Us,(~)

Case 2: {n E co : T ~- pn} =: m • co, but T 17'P~+~. Again, T = T. Let $I E E be

given, consider S :=

max{SI,w

+'m + 1}. Thus, TIE

Us(T) ---* TI

coincides with

T up to p~+,~, thus TI = T/. Finish as in Case 1.

Case 3: m := {n E w : T ~- p,~} 6 co, and T ~- p~,+r~, SO T = T + p~. Let $1 be

given, and consider S :=

max { Sl, co + m + l }.

For TI 6

Us(T), m = {n E co : Tt F

pn}, and

T! F p~o+,~.

So TI = TI + p~. We have to show

T1 E Us,(T). Tf E

Us(T)

+ [Is = (T +

p o) e

[IX

e Us(T) c Us,(T).

4.2. TECHNICAL DEVELOPMENT 143

For (*), argue like this: Tl + p~ k- "~; ~ T~ k p~ ---, ~ --+ T k- p~ ---, ,~ ~ T + p~ i- ~;

for ~ E s as p~ --* ~b is also in s

],-~ is not uniformly continuous: Let $I := co + 1, and assume there is such

S < co + co which proves uniform continuity. Let S < co + m, m < co, and consider

I0:=m,/1 :=mU{co+m},T0 := {p~ :iE Io}U{~p~ :i ~ (co + co) - /o},

T~ := {p~: i e I1} U {-,p~ : i ~ (co +co) - I1}. Then

T~ ~ Us(To),

but p~ E T1 - To,

so ~ r us,(~). []

4.2.3 A measure on

Th;,

integration of the difference

between two logics

Assume in the sequel s to be countable with propositional variables {p~ : i < co}.

The following construction is by Corollary 4.17, 5) a successive refinement of

disjoint partitions of ThL: Set Rio := {The}. Recall that ~ = 2 "(c) and set

R~n := {Th(G[=) : G c F} for 0 < = <

co. (Corollary 4.17, 8) and Lemma 4.3, 4

will give the cardinalities.) Rt := U{Rt~ : n < co} (so each t~ E RI is a subset of

ThL).

We define inductively g : Rt --, B, B the Borel sets of the real line, by g(ThL) :=

[0,1). Let g(Th(G[n)) = [x, xt), card(G[n) = m, say {H[n +1: H[n = G[n} =

_ :~t-x

z--~--).

{hi,-.., h3m}, then for 1 < i < 3 '~ let 9(Th(hi)) := [x + (i 1)-5a- , x + .x,-~

Let some measure # on B be given, define for O E RI #(0) := #(g(0)), let R

be the algebra generated by RI (i.e. the closure of RI under complements and

finite unions), then by construction of 9 (preservation of unions and disjointness

back and forth), # can be extended uniquely to a measure on R, and if ~4 is the

cz-algebra generated by R (i.e. the closure of/~ - or R! - under complements and

countable unions), then there is a unique extension of # to ,4. (This is a standard

result of measure theory.)

Assume now E to be cofinal in co, each S E E finite, E = {Si : i < co}, Si C Sj for

i < j. By Corollary 4.17, 6), and countability of E, A contains all singletons (up

to logical equivalence). Moreover, for each S there is n such that S _C n. Let now

T ~

ThL, then Us(T) = Th(M(T) IS) = U{Th(H In): H C F, H IS = M(T) [5"},

a finite union of sets from R/, so Us(T) E R. As the set {Us(T): T E ThL, S E E}

is countab!e (E is, and for S E E {Us(T): T E The} is finite by finiteness of S),

each open set in Tz is in ~4.

If T :/ T~, n := the least m such that M(T)[S,~ r M(Tf)[S~ is defined (by

Lemma 4.13), we set

0 lifT = Tl

TA3T! := ~ otherwise (n as above)

Fact 4.20 1) TATu <_ max(TAT1, TIATII), and thus also

To~T~ <_ max(ToAT1,..., T~-I~T,~),

2) TATt < TI&T11 --, TAT11 = TI~Ttf.

For two logics [~ and [,-~ I, 1~ z~ [~ I(T) :~ (T)A [,-- I(T) defines a function

[~ A 1~ ~: The ~ [0, 1], and we can define as sketched in the introduction the

Lebesgue integral f(]~ ~ [~ I).

144

CHAPTER 4. LOGIC AND ANALYSIS

We conclude by showing that I~ /~ I "~ I r g', and thus that I~ A t~,, I) is

defined, ifl~ andt~ I are continuous.

Lemma 4.21 Ifl~-, ,I ~-, /are continuous (with respect

to

T~), then f@,

ai~

r)

is defined.

Proof By the above, it suffices

to

show that ],-~ & I n t is A - B-measurable,

i.e. for any Borel set X ~n A t,-~ t)-l(X) E A. As the open intervals generate

the Borel sets, it suffices to show the condition for all open intervals X = (x, x/).

We saw above that T~ g A, so it suffices to show that (]~ ZS l~--

O-l(z,xl)

is

open in Try. Let now T be such that ~ Z~ [~ I)(T) = y E (a:, a:t).

Case l: y = 0, i.e. 1~ (T) ~

I(T),

let n be such

that

[y- g~, y H_ ga_] C _1 1

(x,x'). and nil such that

n C_ Sn,,.

By continuity of ]~, f ,-~ 1, there is n/ such

that I~-,

(Us~,(T)) C C_ Us~,,~"~ (T))

and

I~ ,(Uso,(T))

c

Uso,,d~ ~(T)),

thus

for

Tl E Us~,(T)1~

(T,)~ In (T) <_ ~ and 1~ /(Tf)A 1~ r < ~, so

i n

,(r,)< (r,)al n (T),I~ (T)Z t~ ,(T)al~ ,(T,))

< andl~ al~ c (x,x').

Case2: y : ~. Let n,l and n/suchthat n+l

C_ S .... I~ (gs~,(T)) C Us.,,~"~ (T))

andl~

t(Us.,(T)) C Vs.,,~.. t(T)),

thus for

Tt E Vs.,(T)]~.,

(TI)A[~ (T) < ~s

and !-

,(T,)a

I- ,(T) < ~ I n (T)A I- t(T)

_ ~-zvr, so by : 1 and Fact 4.20,

2) l" (T,')A I~ t(T 0 = ~. So again [~ a I~

t(Us~,(T)) C

(x,x'). Thus,

al~ x,) is open in we are done. []

Finally, we give a very brief sketch of another way of defining a numerical differ-

ence between two theories, which is motivated by the following: Suppose we have

two theories, T and

Tt,

consisting of rules and facts, which are used e.g. to take

preventive action - medical diagnosis, monitoring a power plant etc. Let T be the

correct theory, TI a hopefully good approximation to T. If T t- r but Tt V r we

may not be warned of imminent danger, measured by some cost and probability

of occurrence. Conversely, deducing T! ~- 4, when T V 4; may cause unnecessary

preventive action, a certain cost, too. Going via models, we may assign each

model a cost (separately for both possibilities discussed), and probability, and

define the difference between the two theories as the sum (for both ways) of the

sum of probability*cost over all models where they diverge.

4.2.4 A toy application

Suppose we are given two therapeutical expert systems, and one '~real" expert,

who makes no mistakes and who is taken as a standard. Suppose they differ from

the medical point of view only slightly from the real expert, by their recommen-

dation of an additional drug alleviating a minor symptom in some cases.

Describing the situation in logical terms, we may be given a set of diagnostic

variables sl. 9 s,L representing symptoms, and a number of therapeutical variables

h..-tk representing possible drugs. The expert (system) can then be described

Schlechta K. Nonmonotonic Logics: Basic Concepts, Results, and Techniques

Подождите немного. Документ загружается.