Сапожников С.З. Китанин Э.Л. Техническая термодинамика и теплопередача
Подождите немного. Документ загружается.

191
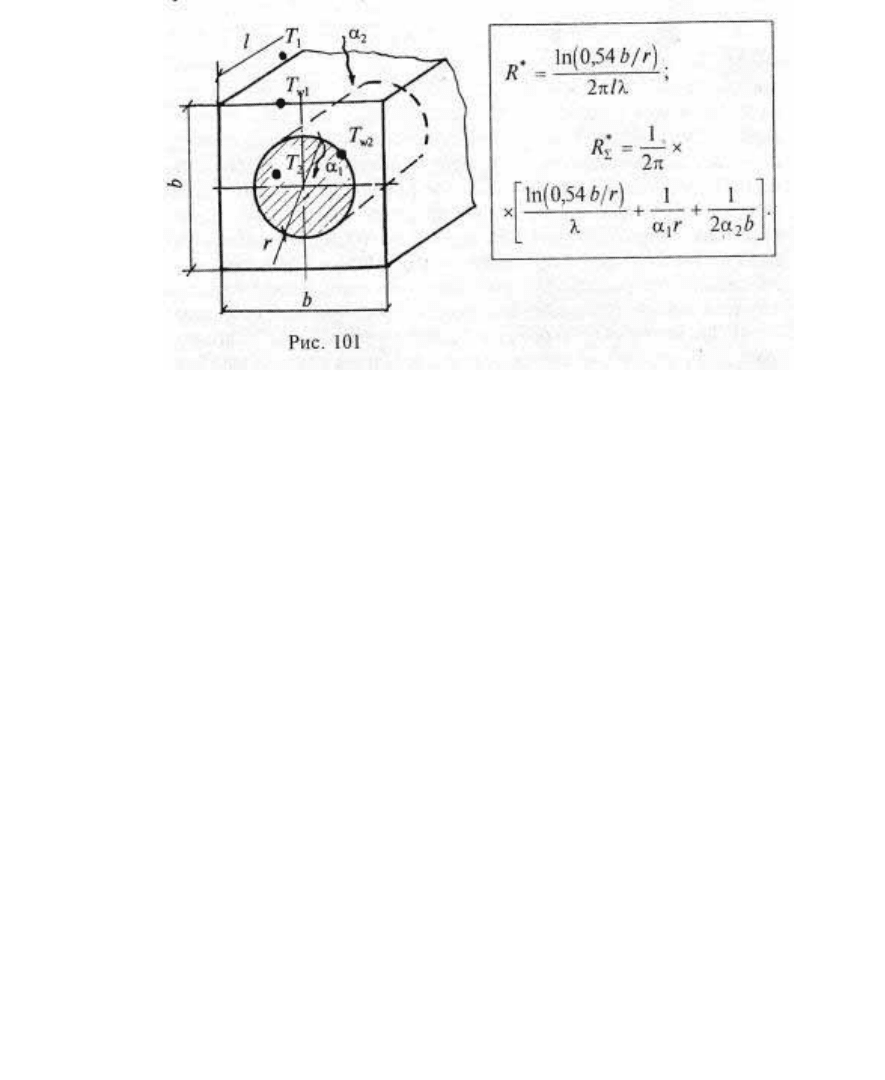
Рис. 101.
2.5.2. Графический метод
Если тело имеет сложную форму, то рассчитать поле
температуры, даже стационарное, методом ЭТА затруднительно.
Удобней обратиться к графическому методу, который требует
лишь простейших расчетов и, как сказано в одном руководстве,
обладает “поразительной точностью”.
Графический метод реализует векторную форму закона
Фурье, согласно которому в окрестностях любой точки тела
изотермическая поверхность перпендикулярна вектору теплового
потока. Если изотермические поверхности проведены “достаточно
густо”, то вместо векторов можно провести кривую q = const
(линию теплового тока), пересекающую все изотермические
поверхности по нормалям (рис. 102).
192
Рис. 102.
Графически это означает, что в каждой точке сечения линия
тока перпендикулярна изотерме, а вектор теплового потока
направлен к линии тока по касательной. Если построить
пересекающиеся семейства линий T = const и q = const, которые
будут в каждой точке пересечения взаимно перпендикулярны, то
удастся определить тепловой поток и поле температуры в сечении
тела.
Решение задачи разделяют на три этапа.
1. Вычерчивают, соблюдая масштаб, сечение расчетной
области.
2. Наносят линии T = const и q = const, добиваясь, чтобы
диагонали косоугольных четырехугольников делили одна другую
пополам и были взаимно перпендикулярны. Изотермы, кроме того,
должны быть перпендикулярны адиабатным границам (поскольку
на них q = 0), а также осям симметрии области, если они есть.
3. Уточняют расположение линий сетки, пока не будут
выполнены положения второго этапа, а затем определяют тепловой
поток, пользуясь законом Фурье.

193
Рассмотрим в качестве примера составную область (см. рис.
102), включающую Н-образную “вставку” (похожее сечение может
иметь теплоизолированная стенка кузова, усиленная армирующим
ребром). На границах области заданы температуры ,и
21 ww
TT т. е.
поддерживаются граничные условия I рода. Требуется определить
тепловой поток, идущий через “вставку”, — ее обычно называют
тепловым мостиком (если автомобиль оставили на улице, а ночью
были заморозки, все такие мостики утром станут ясно видны: на
них по-другому, чем на прочих местах, оседает иней).
Считаем задачу стационарной, а все границы “вставки”, кроме
выделенных жирной линией, — адиабатными; теплопроводность
материала вставки постоянна и равна λ. Исходя из соображений
симметрии, вычертим в удобном масштабе 1/2 сечения вставки, а
затем проделаем операции, указанные в этапах 1 и 2. Тепловой
поток мы разделили на составляющие Q
1
, Q
2
, Q
3
и Q
4
, причем их
сумма равна общему тепловому потоку:
.
1
∑
=
Σ
=
n
i
i
QQ
(2.102)
Для каждой ячейки (одна из них показана на рис. 102) можно
записать уравнение Фурье
x
TT
y
Q
q
iii
i
∆
−
λ=
∆
=
+1
(2.103)
(в формуле (1.103) полагаем, что в направлении, перпендикулярном
плоскости чертежа, размер ∆z = 1). Поскольку в каждой ячейке ∆x =
∆y, перепад температур между соседними изотермами будет
одинаковым. Если теперь между изотермами на чертеже М
промежутков (у нас М= 13), то
(
)
()
.;;
21
2121
1 ww
ww
i
ww
ii
TT
M
x
y
M
TT
Q
M
TT
TT −
λ
=
∆
∆
−
λ
=
−
=−
+
Условие ∆x = ∆y — одно из очень важных: именно оно
определяет, с каким интервалом следует проводить линии обоих
семейств (чем больше линий, тем точнее решение). Вначале задают
величину ∆y (например, так, чтобы изотермы шли с шагом в 5 или

194
10 К), а потом определяют число “каналов” (Q = const по
соотношению ∆x = ∆y; при этом линии тока разделят сечение на N
частей (у нас N = 4), поэтому
.
i
NQQ
=
Σ
Формула (2.104) примет вид
(
)
()
.
13
4
21
21
1
ww
ww
n
i
ii
TT
MM
TT
NNQQQ −
λ
=
−λ
===
∑
=
Σ
(2.104)
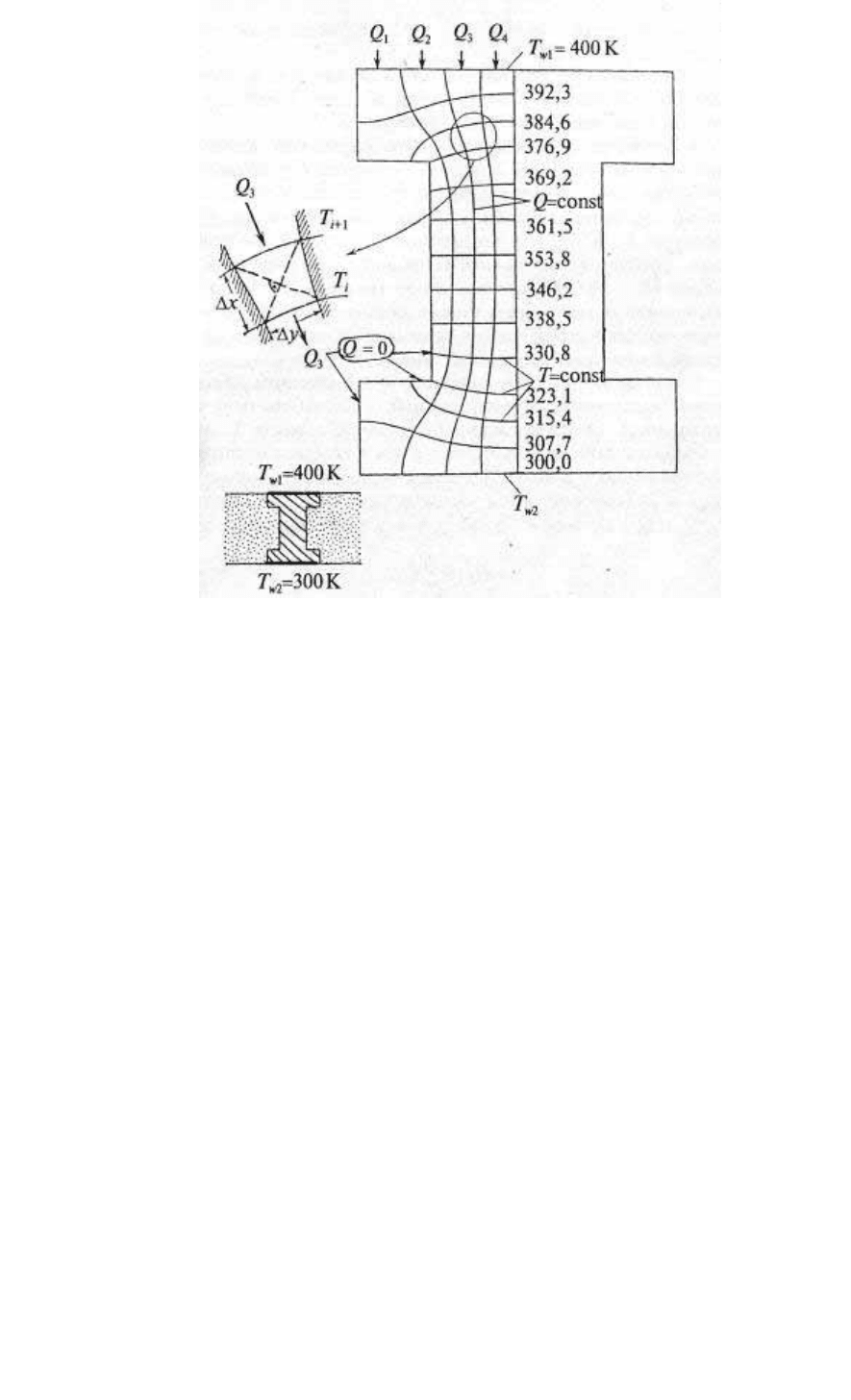
Теперь можно “оцифровать” чертеж: если, например, Т
w1
=
400 К, Т
w2
= 300 К, то изотермы пойдут с шагом 100/13 = 7,7 К.
Отношение N/М = S называют формфактором теплопровод-
ности; с учетом такого обозначения тепловой поток
()
,
21
TSTTSQ
ww
∆
λ
=
−
λ=
Σ
(2.105)
где ∆T — наибольший перепад температуры на исследуемой
области.
Мы провели расчет на единицу длины “вставки” (∆z = 1); в
общем случае величина S, как следует из формулы (2.105), должна
иметь размерность длины
[]
[
]
[
]
[
]
[][]
[]
.м
КВт
КмВт
=
⋅
⋅
⋅
=
∆λ
=
Σ
T
Q
S
Значения S заранее рассчитывают для систем,
распространенных в практике, а затем сразу переходят к оценке
Σ
Q
по формуле (2.105). Величину S можно определить и графическим
методом, а иногда — даже аналитически.
Показано, в частности, что для пластины размерами h×b×δ S =
hb/δ, а для полого цилиндра D × d × h —
()
Dd
h
S
ln
2
π
= (см. рис. 74).
Hа рис.103 представлены значения формфактора S для цилиндра с
эксцентричным каналом (рис. 103,а), бруса с каноническим каналом
(рис. 103,б), канала круглого сечения (рис. 103,в) и цилиндрической
полости конечной глубины в полуограниченном теле (рис. 103,г).
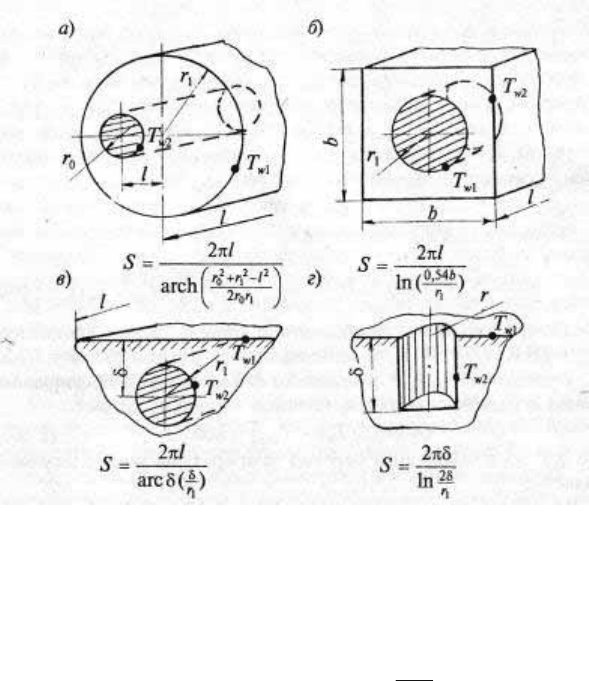
195
Рис. 103.
Заметим, что формфактор S связан с термическим
сопротивлением тела R* зависимостью
,
1
S
R
λ
=
∗
поэтому формулы
и таблицы в обоих случаях взаимозаменяемы: достаточно,
например, сопоставить формулы, приведенные на рис. 101 и 103,б.
Модификации графического метода существуют и для других
видов граничных условий, но они менее удобны. Еще одно
ограничение связано с тем, что метод применим лишь для
стационарных задач: при решении задач нестационарных пришлось
бы
для каждого выбранного момента проводить свой расчет,
корректируя температурное поле на границе по результатам
предшествующих выкладок.
2.5.3. Метод конечных разностей
Основная идея метода состоит в том, что непрерывный
процесс теплопередачи заменяют дискретным; при этом изотермы
из плавных линий превращаются в ломаные. Математически метод
конечных разностей означает замену дифференциального
уравнения теплопроводности алгебраическим уравнением, где роль
приращений
x
T
∂τ∂∂ ,, выполняют конечные разности .,,
x
T
∆τ∆∆

196
Рис. 104.
Впервые такой подход реализовал немецкий теплотехник
Э. Шмидт в 1924 г.; следуя его идеям, рассмотрим задачу
нестационарной теплопроводности пластины при граничных
условиях I рода с произвольным начальным распределением
температуры.
Разобьем пластину (рис. 104) на слои произвольно малой
толщины ∆х и присвоим им индексы n–1, n, n+1,... Интервалам
времени ∆τ присвоим обозначения k
–1, k, k+1,... Температуру n-го
слоя в момент времени k будем обозначать Т
n,k
.
Заменим дифференциальное уравнение Фурье
2
2
x
T
a
T
∂
∂
=
τ∂
∂
конечно-разностным приближением
.
2
2
x
T
a
T
∆
∆
=
τ∆
∆
(2.106)
Переход к алгебраическому уравнению (2.106) означает, что
температура в сечении пластины меняется по ломаной линии — она
соединяет точки 1, 2, 3, ..., лежащие в среднем сечении каждого
слоя толщиной ∆х.
Соединим эти точки для некоторого момента τ = k∆τ и
получим ломаную 1–2–3.
В пределах любого n-го слоя перелом линии означает, что aналог
частной производной
x
T
∆
∆
имеет два значения — “левое”
−
⎟
⎠
⎞
⎜
⎝
⎛
∆
∆
x
T
и
“правое”
+
⎟
⎠
⎞
⎜
⎝
⎛
∆
∆
x
T
:
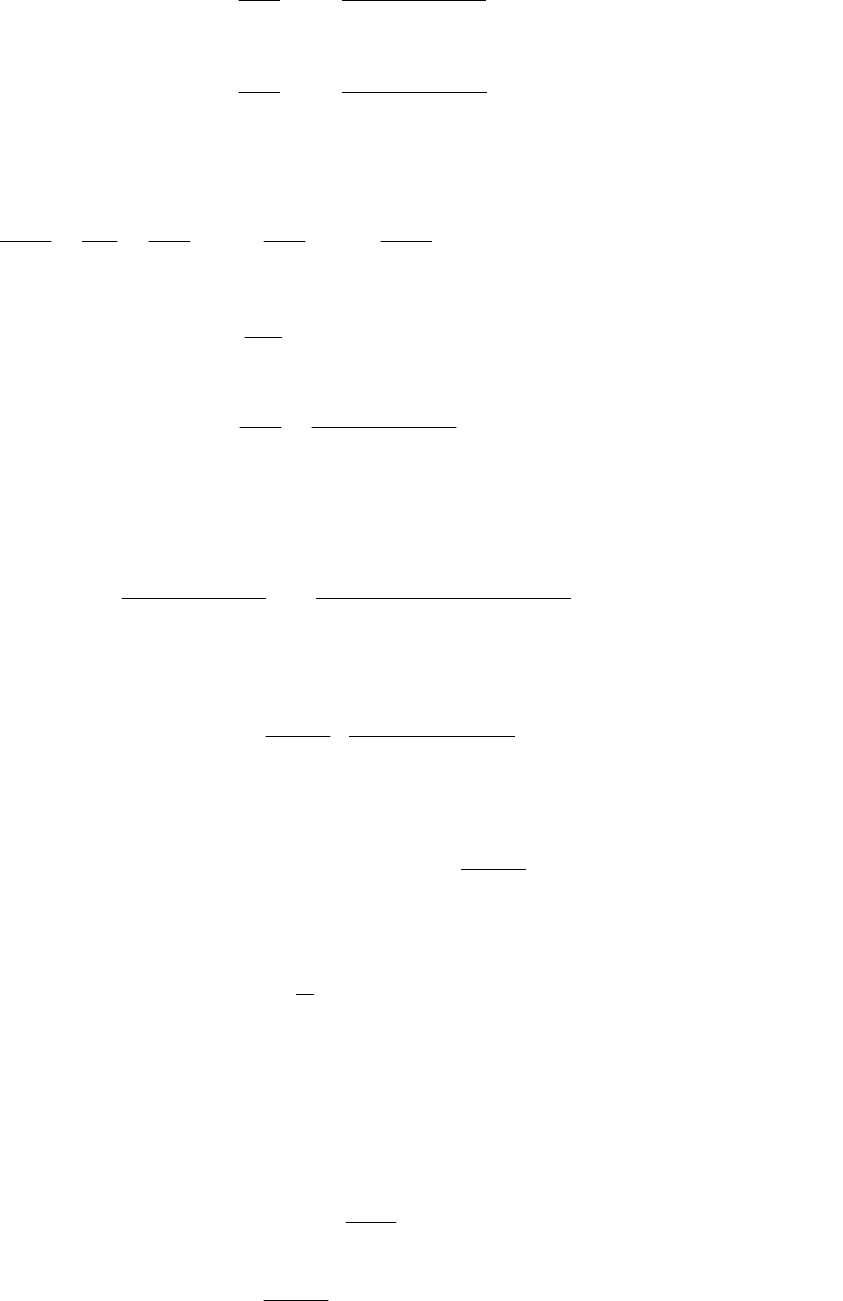
197
.
;
,,1
,1,
x
TT
x
T
x
TT
x
T
knkn
knkn
∆
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∆
∆
∆
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∆
∆
+
+
−
−
Aналог второй частной производной
()
knknkn
TTT
x
x
T
x
T
x
x
T
,,1,1
22
2
2
11
−+
∆
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∆
∆
+
⎟
⎠
⎞
⎜
⎝
⎛
∆
∆
∆
=
∆
∆
−+
+−
(2.107)
Аналог производной
τ∂
∂T
.
,1,
τ
∆
−
=
τ∆
∆
+ knkn
TT
T
(2.108)
С учетом подстановок (2.107) и (2.108) перепишем уравнение
(2.106):
;
2
,,1,1,1,
x
TTT
a
TT
knknknknkn
∆
−
+
=
τ
∆
−
−++
(2.108)
отсюда
.
2
2
,
,1,1
2
,1,
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
∆
τ∆
=−
−+
+
kn
knkn
knkn
T
TT
x
a
TT
(2.109)
Поскольку ∆х и ∆τ мы задали произвольно, их соотношение может
быть любым. Выберем его так, чтобы
1
2
2
=
∆
τ
∆
x
a
, тогда из равенства
(2.109) получим
(
)
,
2
1
,1,11, knknkn
TTT
−++
+=
(2.110)
т. е.
температура в n-м слое в момент (k+1)∆τ равна полусумме
температур в двух соседних слоях в момент k∆τ. На рис. 104
решение (2.110) представлено графически: точка 2 получается, если
соединить отрезком прямой точки 1 и 3.
Поскольку величина
2
x
a
∆
τ
∆
равна числу Фурье для слоя
толщиной ∆х, условие
1
2
2
=
∆
τ
∆
x
a
можно записать короче: Fо = 0,5.
198
Таким образом, для решения задачи методом Шмидта
необходимо:
разбить сечение на n слоев толщиной ∆х каждый;
выбрать интервал времени ∆τ, удовлетворяющий условию Fо
= 0,5;
задать начальное распределение температур 1–2–3–...;
последовательно определить температуры в моменты ∆τ,
2∆τ,..., k∆τ,..., используя соотношение (2.110) или эквивалентное
ему графическое построение.
Э. Шмидт предложил свой метод именно как
графический,
хотя сейчас его используют в основном как компьютерный.
Существуют двух- и трехмерные варианты метода конечных
разностей.
Дальнейшее развитие описанный подход получил в 1946 г.,
когда А.П. Ваничев предложил его модификацию —
метод
элементарных балансов, который позволил решать задачи
теплопроводности для составных тел и для сред с переменными
теплофизическими свойствами.
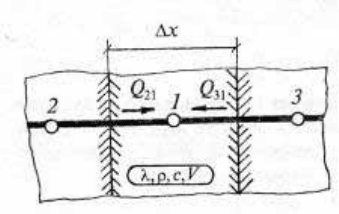
Метод элементарных балансов (применительно к одномерным
задачам) предполагает, что теплоемкость каждого n-го слоя
“сосредоточена” в некоторой точке 1 (рис. 105); со своими
“соседями” — точками 2 и 3 — точка 1 соединена
тепловыми
связями, по которым передается теплота. В основе метода
Ваничева лежат три постулата.
Рис. 105.
1. Изменение температуры между расчетными точками
(узлами) происходит по линейному закону и определяется
термическим сопротивлением тепловых связей.
2. Изменение температуры во времени происходит скачками.
3. Увеличение энтальпии элементарного объема,
прилегающего к данному узлу, пропорционально приращению
температуры в этом узле.
Если в сечении выделить слой ∆х, а все расчеты вести
для
пластины единичной площади, то элементарный объем слоя
199
(
)
.1
2
xxxV ∆=⋅∆⋅∆=
Теплота, переданная слою по связи 2–1, на основании
постулата 1,
()
,
1221
τ∆∆−
∆
λ
= xTT
x
Q
а переданная по связи 3–1–
()
;
1331
τ∆∆−
∆
λ
= xTT
x
Q
здесь T
1
, T
2
, T
3
— температуры узлов, рассчитанные в один и тот же
момент.
За время ∆τ температура узла 1 изменится, поскольку к нему
подведена теплота Q
21
,+Q
31
; это изменение, в силу постулата 3,
определится из соотношения
() ()
,2
132312111
TTT
x
x
QQTTVc −+τ∆
∆
∆
λ
=+=τ∆−
′
ρ
(2.111)
где
1
T
′
— температура узла 1, рассчитанная в конце интервала
времени ∆τ (в соответствии с постулатом 2 температура узла
меняется скачком).
Соотношение (2.111) — уравнение теплового баланса (отсюда
и название метода); из него следует, что
.2
1
1321
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
ρ
τ∆λ
+−+
ρ
τ∆λ
=
′
Vc
T
TTT
Vc
T
Если учесть, что
()
()
,Fo,,
2
2
=
∆
τ∆
∆==
ρ
λ
x
a
xVa
Vc
то
последнее равенство примет вид
.2
Fo
1
Fo
1321
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−++=
′
TTTT
(2.112)
Потребуем, как и прежде, чтобы Fо = 0,5, тогда
.
2
32
1
TT
T
+
=
′
(2.113)
Как видим, уравнение (2.113) имеет тот же смысл, что и
уравнение (2.110). В то же время условие Fо = 0,5 для уравнения
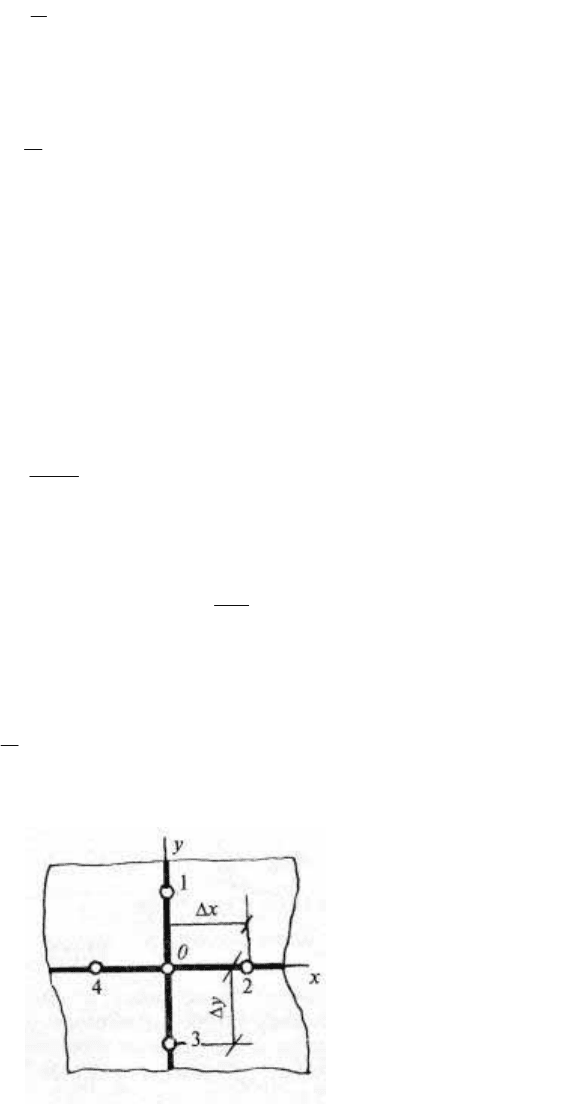
200
(2.112) не является обязательным; можно задавать любые значения
Fо < 0,5. Например, при Fо = 1/3 равенство (2.112) принимает вид
()
,
3
1
1321
TTTT ++=
′
а при Fо = 1/4 —
()
.2
4
1
1321
TTTT ++=
′
В правую часть этих формул входит величина T
1
: для расчета
каждой последующей температуры в узле 1 надо знать предыдущее
ее значение. Чем меньше Fо, тем точнее решение, но одновременно
с точностью, увеличивается трудоемкость (или применительно к
компьютерному варианту — время счета).
Для двумерных задач теплопроводности составляется
аналогичная расчетная схема (рис. 106); если положить,
что
,Foa,
2
δ
τ
∆
=δ=∆=∆
a
yx то в узле 0 в каждый последующий
момент времени температура
,2
Fo
1
Fo
043211
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−++++=
′
TTTTTT
а при Fо = 1/4
()
.
4
1
43211
TTTTT +++=
′
Рис. 106.
Трехмерные задачи решают, рассматривая пространственные
тепловые связи.
И метод Шмидта, и метод Ваничева реализуют
явные
конечно-разностные схемы: каждую последующую (во времени)
