Salby M.L. Fundamentals of Atmospheric Physics

Подождите немного. Документ загружается.

420

13 The Planetary

Boundary Layer

13.4 Ekman Pumping

Turbulent drag inside the boundary layer drives the large-scale motion out

of geostrophic equilibrium and introduces a divergent component (Sec. 12.3).

To satisfy continuity, that divergence must be compensated by vertical motion,

which imposes a secondary circulation on the

O(Ro ~

geostrophic flow in

the free atmosphere. Frictional convergence (divergence) inside the boundary

layer leads to rising (sinking) motion over surface low (high) pressure (Fig.

12.7).

Vertical motion atop the boundary layer is related to the circulation in the

free atmosphere through the boundary condition (13.17.3). By continuity, it

must also be related to the convergence of horizontal mass flux inside the

Ekman layer, which follows from the cross-isobaric component ~. Integrating

vertically over the boundary layer obtains the column-integrated mass flux

across isobars

M = po(O)

9dz

= po(O)

Uge -~z

sin

7zdz,

(13.25.1)

which reduces to

M = P~

23, Ug.

(13.25.2)

Since ~ is directed toward low pressure, the column-integrated mass flux across

isobars can be expressed

M = P~ x Vg.

(13.26)

By integrating the continuity equation (13.10.4) in a similar fashion, we obtain

V z 9 M + po(O)wo

= 0, (13.27)

where w 0 denotes the vertical velocity or

Ekman pumping

atop the boundary

layer. Incorporating (13.26) then yields

Wo = ~ srg(O), (13.28.1)

where

srg(0)- V2@(0) (13.28.2)

is the geostrophic vorticity at the base of the free atmosphere. According

to (13.28), Ekman pumping is directly proportional to the vorticity above the

boundary layer. For values used previously to evaluate 7 and for srg = 10 -5 s -1

typical of quasi-geostrophic motion, (13.28) gives

of order 5 mm s -1.

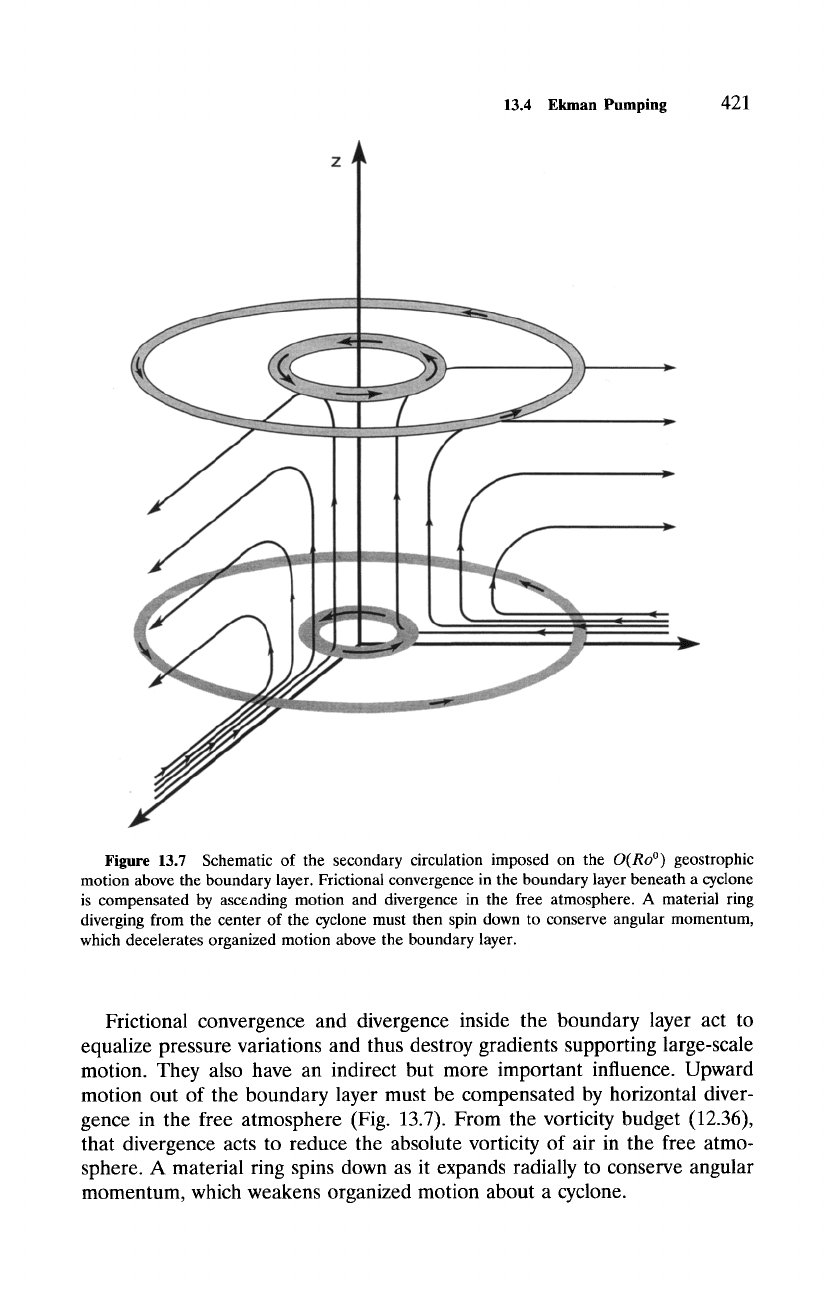
13.4 Ekman Pumping

421

Figure 13.7 Schematic of the secondary circulation imposed on the

O(Ro ~

geostrophic

motion above the boundary layer. Frictional convergence in the boundary layer beneath a cyclone

is compensated by ascending motion and divergence in the free atmosphere. A material ring

diverging from the center of the cyclone must then spin down to conserve angular momentum,

which decelerates organized motion above the boundary layer.

Frictional convergence and divergence inside the boundary layer act to

equalize pressure variations and thus destroy gradients supporting large-scale

motion. They also have an indirect but more important influence. Upward

motion out of the boundary layer must be compensated by horizontal diver-

gence in the free atmosphere (Fig. 13.7). From the vorticity budget (12.36),

that divergence acts to reduce the absolute vorticity of air in the free atmo-

sphere. A material ring spins down as it expands radially to conserve angular

momentum, which weakens organized motion about a cyclone.

422

The Planetary Boundary Layer

Under barotropic stratification, the horizontal velocity in the free atmo-

sphere is independent of height. Integrating the continuity equation (13.10.4)

from the top of the boundary layer to a height h where w has been driven to

zero then yields

w o = hVz.V

= hV z .Va,

(13.29)

where

v a

is the ageostrophic velocity associated with the secondary circulation.

The vorticity equation for quasi-geostrophic motion (12.47) restricted to an

f plane reduces to

dt - -foVz" Va"

With (13.29) and (13.28), this becomes

at = 2yh ~g

(13.30)

9 9 ~g

~ "

(13"31/

A vorticity anomaly like that accompanying a cyclone then decays exponen-

tially as

where

~'u=exp --- ,

,l" E

(13.32.1)

~'E = ~, 2h 2 j (13.32.2)

is an Ekman e-folding time. Hence, the secondary circulation imposed by

Ekman pumping causes the primary circulation to spin down. This process in-

volves no actual dissipation, but rather follows from a redistribution of angular

momentum when absolute vorticity is diluted over a wider region. By Stokes'

theorem, the circulation along an expanding material contour

s(x, y)

F= f vg.ds

= f,,

(13.33)

remains unchanged. (Should a disturbance's vertical structure make

= 0 at

the surface, Ekman pumping and divergence in the free atmosphere vanish,

eliminating spin down.) In practice, the depth h over which spin down occurs

is shaped by static stability in the free atmosphere. For values representative

Problems

423

of the troposphere, (13.32) gives an e-folding time of order days, which is an

order of magnitude shorter than the timescale for direct frictional dissipation

in the free atmosphere.

Suggested Reading

A First Course in Turbulence

(1972) by Tennekes and Lumley presents an in-

troduction to the subject at the graduate level and includes a formal treatment

of turbulent energetics.

Statistical Fluid Mechanics

(1973) by Monin and Ya-

glom is an advanced treatment that includes a wide range of observations and

a Lagrangian description of turbulent dispersion.

An Introduction to Boundary Layer Meteorology

(1988) by Stull is a nice devel-

opment at the graduate level. An extensive collection of recent observations is

included in

The Structure of the Atmospheric Boundary Layer

(1989) by Sorbjan.

Hydrodynamic Instability

(1985) by Drazin and Reid contains a formal treat-

ment of shear instability at the graduate level.

Problems

13.1.

13.2.

13.3.

13.4.

13.5.

Calculate the Reynolds number for the following flows: (a) Stokes flow

about a spherical cloud droplet (Problem 9.15) of radius 10 ~m and fall

speed of 3 mm s -a, (b) cumulus convection of characteristic dimension

1 km and velocity 1 m s -1, and (c) a midlatitude cyclone of characteristic

dimension 10 3 km and velocity 5 m s -a.

Express the Reynolds number as a ratio of timescales and then use

them to interpret the criterion for the onset of turbulence.

Estimate the height of the turbopause based on characteristic length

and velocity scales of 1 km and 10 m s -a, respectively.

In terms of temperature, water vapor mixing ratio, and ozone mixing

ratio, contrast the state of an air parcel before and after encountering

(a) the boundary layer and (b) cumulus convection.

Frictional dissipation is an essential feature of turbulence because it

cascades energy from large scales of organized motion to small scales,

on which molecular diffusion operates efficiently. The specific energy

dissipation rate for homogeneous isotropic turbulence is described by

U 3

L '

where U and L are the characteristic velocity and length scales of the

large-scale motion that drives the cascade. Hence, the rate of energy

dissipation, which occurs almost entirely at small scales, is dictated by

the motion at large scales, which is nearly inviscid. Use this result to

estimate the rate at which energy is dissipated inside a cumulonimbus

424 13 The Planetary Boundary Layer

cloud of characteristic dimension 10 km and velocity 10

m s -1.

Compare

this value with the 1000 MW generated by a large urban power plant.

13.6. For the cumulonimbus cell in Problem 13.5, estimate the precipitation

rate necessary to sustain the motion.

13.7. Derive the approximate vertical momentum balance (13.4).

13.8. Establish the flux form of the momentum equations (13.8).

13.9. Contrast the signs of the momentum flux in (13.11) and the heat flux

in (13.12) in light of their appearance in the primitive equations.

13.10. Verify that (13.18) is the solution of the boundary-layer equations, sub-

ject to appropriate boundary conditions.

13.11. Recover (13.20) governing mean motion inside the surface layer.

13.12. Demonstrate that the turbulent vertical heat flux must be positive (neg-

ative) under unstable (stable) stratification.

13.13. Show that divergence associated with the secondary circulation above

the boundary layer does not alter the circulation F = ~ v. ds along a

material contour.

13.14. Derive expression (13.27) for vertically integrated conservation of mass.

13.15. A midlatitude cyclone is associated with the disturbance height in the

lower troposphere

(x2+y )

z'=-Zexp - 2L 2 ,

where Z = 200 m, L = 1000 km, y is measured from 45 ~ and the

boundary layer has an eddy diffusivity of 10 m2s -1. Calculate the max-

imum vertical velocity atop the boundary layer.

13.16. Observations reveal a nearly logarithmic variation with height of mean

wind below 100 m above prairie grass land, which has a roughness

length of 4 cm. If the mean wind is 5 m s -1 at the top of this layer,

calculate the stress exerted on the ground.

13.17. Inside a well-mixed boundary layer of depth h, convection makes mean

horizontal motion and potential temperature invariant with height (Fig.

13.5), rendering the flux-gradient relationship inapplicable. The verti-

cal momentum flux then decreases linearly with height from a surface

maximum described by

w'v'ls = --edible,

where Cd is a dimensionless drag coefficient. (a) Construct a counterpart

of the Ekman equations (13.15) governing mean motion inside the well-

mixed layer to show that the effect of turbulence is then equivalent to

Rayleigh friction (Sec. 12.3). (b) Determine ~ if Vg = Ugi above the well-

mixed boundary layer. (c) Calculate the timescale of Rayleigh friction

for h = 1 km, Ca = 5.0

x 10 -3,

and a mean wind speed of 5 m s -1.

Problems

425

13.18. Estimate how strong vertical shear must become before turbulence

forms under stability representative of (a) mean conditions in the tro-

posphere:

N 2 --

1.0

x 10-4S -2

and (b) mean conditions in the strato-

sphere:

N 2 --

6.0

x 10-4S -2. (C)

How would these values be affected if,

locally, isentropic surfaces are steeply deflected from the horizontal?

13.19. Calculate the characteristic spin-down time due to Ekman pumping for

a cyclone at 45 ~ vertical motion extending to the tropopause at 10 km,

and an eddy diffusivity inside the boundary layer of 10

m2s -2.

Compare

this spin-down time with the timescale of radiative damping.

13.20. The contrail formed from the exhaust of a commercial jet flying at 200

mb contains liquid water. At a distance x from the jet, the contrail has a

temperature

T(x)

and a mixing ratio for total water

rt(x ).

The contrail

dissolves some distance

x d

downstream of the jet through entrainment

with ambient air, of temperature T~ and mixing ratio ra. Immediately aft

of the jet, the exhaust plume has temperature T(0) - T o and total water

mixing ratio rt(0 ) - r 0. (a) Formulate a differential equation governing

rt(x ),

in terms of the entrainment length L -1 -

d(lnm)/dx,

which

characterizes the rate at which the contrail expands through mixing

with ambient air (See. 7.4.2). (b) Derive expressions for

rt(x)

and

T(x).

rw(x ).

(d) Determine the distance

x d

at which the contrail dissolves

for L - 100 m, r 0 - 4 g

kg -1,

r a -

0.05 g kg -1, T O - -20 ~ C, and

T a -

-50 ~ C. (e) As in part (d), but under the warm moist conditions"

T a -

-30 ~ C,

r a -

1.25 g kg -1, T o - 0 ~ C, symbolic of conditions inside

the warm sector of an advancing cyclone.

Chapter 14

Atmospheric Waves

The governing equations support several forms of wave motion. Atmo-

spheric waves are excited when air is disturbed from equilibrium (e.g., me-

chanically when air is displaced over elevated terrain or thermally when air

is heated inside convection). By transferring momentum, wave motions com-

municate the influence of one region to another. This mechanism enables the

troposphere to drive the stratosphere out of radiative equilibrium (Fig. 8.27)

and tropical convection to influence the extratropical circulation.

14.1 Description of Wave Propagation

Wave motions are possible in the presence of a positive restoring force, which,

by opposing disturbances from equilibrium, supports local oscillations in field

properties. Buoyancy provides such a restoring force under stable stratification

(Sec. 7.3). The compressibility of air provides another. Variations with latitude

of the Coriolis force provide yet another restoring force, which will be seen to

support large-scale atmospheric disturbances.

14.1.1 Surface Water Waves

The description of wave motion is illustrated with an example under nonro-

tating conditions that will serve as a model of buoyancy oscillations in the

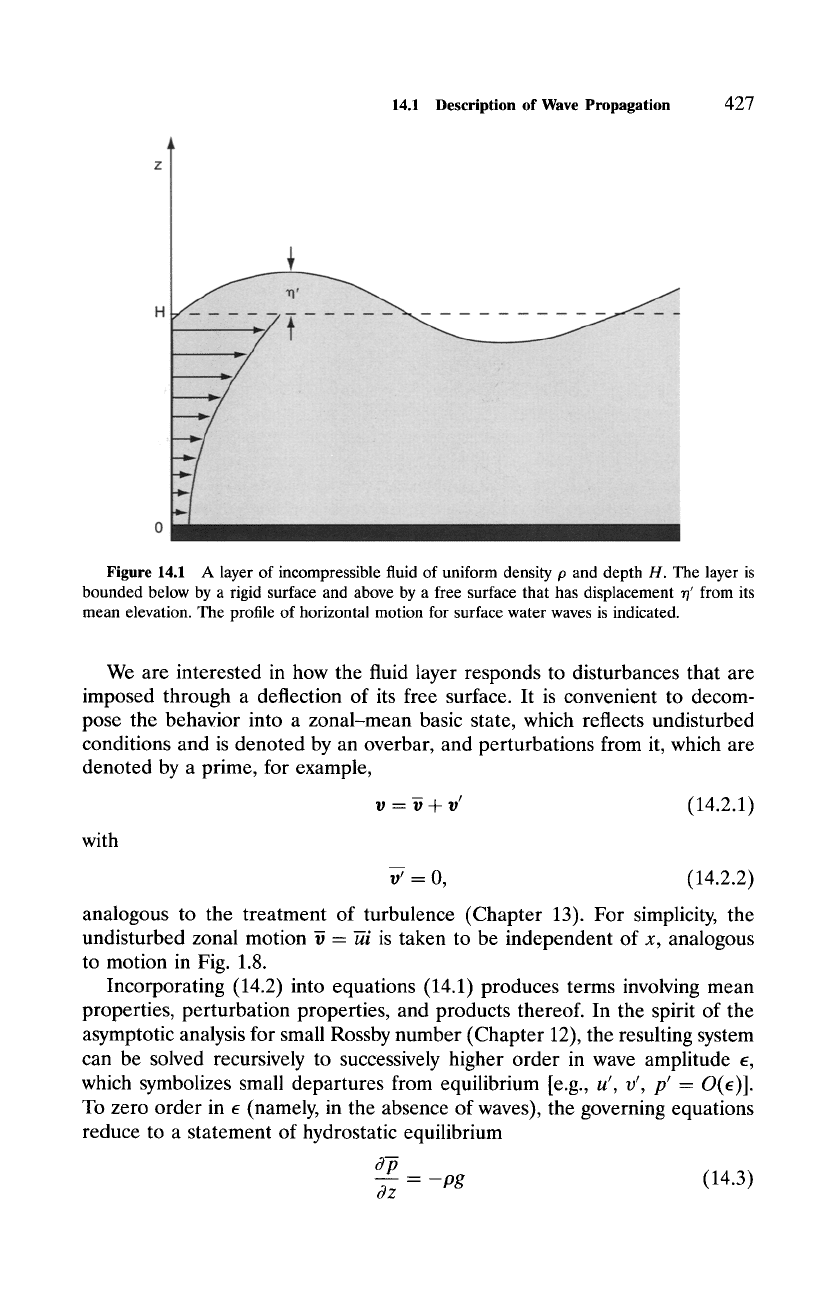
atmosphere. Consider disturbances to a layer of incompressible fluid of uni-

form density p and depth H (Fig. 14.1). The layer is bounded below by a rigid

surface and above by

a free surface,

namely, one that adjusts position to relieve

any stress. Motions inside this layer are governed by

P--d-t = -Vp - gk

(14.1.1)

V. v = O, (14.1.2)

with v and V referring to 3-dimensional vector quantities.

426

14.1

Description of Wave Propagation

427

Figure

14.1 A layer of incompressible fluid of uniform density p and depth H. The layer is

bounded below by a rigid surface and above by a free surface that has displacement ,/' from its

mean elevation. The profile of horizontal motion for surface water waves is indicated.

We are interested in how the fluid layer responds to disturbances that are

imposed through a deflection of its free surface. It is convenient to decom-

pose the behavior into a zonal-mean basic state, which reflects undisturbed

conditions and is denoted by an overbar, and perturbations from it, which are

denoted by a prime, for example,

with

v - -~ + v'

(14.2.1)

v'- O, (14.2.2)

analogous to the treatment of turbulence (Chapter 13). For simplicity, the

undisturbed zonal motion ~ = Ki is taken to be independent of x, analogous

to motion in Fig. 1.8.

Incorporating (14.2) into equations (14.1) produces terms involving mean

properties, perturbation properties, and products thereof. In the spirit of the

asymptotic analysis for small Rossby number (Chapter 12), the resulting system

can be solved recursively to successively higher order in wave amplitude E,

which symbolizes small departures from equilibrium [e.g., u', v', p' - O(e)].

To zero order in E (namely, in the absence of waves), the governing equations

reduce to a statement of hydrostatic equilibrium

= -pg

(14.3)

428

Atmospheric Waves

that must be satisfied by the mean state. To first order in e and with the basic

state balance (14.3) eliminated, the governing equations reduce to

Dr'

= -Vp' (14.4.1)

where

V. v'= 0, (14.4.2)

D 3 3

= -- --- (14.4.3)

Dt 3t + U3x

defines the material derivative following the mean motion. Linear in pertur-

bation quantities, equations (14.4) govern the wave field. However, because

they neglect products of perturbation quantities resulting from the advective

terms

v'. Vv',

the first-order equations ignore influences the waves exert on

the mean state. Such feedback is reflected in the equations accurate to sec-

ond order in ~, which, upon eliminating the zero- and first-order balances and

averaging zonally, yields

-- =-(v'. vv')

o(v'u') o(w'u')

= ~. (14.5)

Oy 0z

Quadratic terms appearing on the right-hand side of (14.5) represent the con-

vergence of an eddy momentum flux that forces the zonal-mean motion~just

like the turbulent eddy fluxes forcing mean motion in (13.10). Corresponding

changes in ~ then reflect second-order corrections to the zeroth-order steady

motion.

In the limit of small wave amplitude, to which the development is now

restricted, second-order terms in (14.5) are small, so the basic state may be

regarded as steady. Motion in the fluid layer is then described by the equa-

tions accurate to first order in wave amplitude, which are said to have been

linearized.

If the basic state is in uniform motion, so that ~ is independent

of position, applying V. to (14.4.1) and incorporating (14.4.2) leads to the

consolidated equation for the perturbation pressure

VZp ' -0. (14.6)

With fixed boundaries, Laplace's equation cannot describe wave propagation

because it is diagnostic. However, boundary conditions governing the free

surface introduce time dependence to make the complete system prognostic.

The free surface, which is an interface between fluids, must satisfy two

conditions. The

dynamic condition

requires the stress and hence total pressure

to vanish. With hydrostatic equilibrium for the mean state (14.3), the total

pressure on the free surface is

P - -Pg~7'

+ P' z = H + r/, (14.7.1)

14.1

Description of Wave Propagation

429

where rt' is the deflection of the free surface from its undisturbed elevation.

Then the perturbation pressure at the top of the layer is given by

P' = Pgn' z = H,

(14.7.2)

which may be evaluated at the mean elevation of the free surface to the same

degree of approximation inherent in (14.6). The

kinematic condition

requires

the free surface to be a material surface, so its vertical displacement must

satisfy

dr/'

= w z - H 4- r/'. (14.8.1)

In the limit of small amplitude, this reduces to

Dr/' = w' z- H. (14.8.2)

Combining the dynamic condition (14.7.2) and the kinematic condition (14.8.2)

obtains

1 Dp' = w' z- H,

(14.9.1)

pg Dt

which, when incorporated into the vertical momentum equation, gives the

upper boundary condition

1 DZp ' dp'

= z-H.

(14.9.2)

g Dt 2 3z

Another boundary condition applies at the base of the layer, where vertical

motion must vanish identically. Then the vertical momentum equation requires

ap'

=0 z-0. (14.10)

14.1.2 Fourier Synthesis

Consider a small disturbance to the free surface. The system is positively

stratified because the density of the liquid is much greater than that of the

overlying air, which is ignored. Buoyancy then provides a positive restoring

force, which drives fluid back toward its undisturbed position and sets up

oscillations. As a result, a compact initial disturbance radiates away in the

form of waves.

Wave activity radiating away from the initial disturbance may assume a

complex form (e.g., because the structure of the disturbance imposes that

form initially or because individual components of the wave field propagate

differently). Equations governing the wave field are linear in perturbation

quantities and have coefficients that are independent of position and time.