Salby M.L. Fundamentals of Atmospheric Physics

Подождите немного. Документ загружается.

410

13 The Planetary Boundary Layer

(13.10.1) is forced by the convergence of eddy x momentum flux and so forth.

Then, according to the discussion in Sec. 10.6, fluxes of x momentum carried

by the three components of fluctuating velocity

rxx = -poU'U'

(13.11.1)

7"xy "- -- Po Ut l) t

(13.11.2)

rxz - -pou'w '

(13.11.3)

constitute stresses in the x direction exerted on the mean flow by turbulent

motions. Referred to as

Reynolds stresses,

they are responsible for turbulent

drag on the mean motion of an air parcel. Collectively, the Reynolds stresses

define a turbulent stress tensor ~- -

-poV'V',

which is a counterpart of the

stress tensor in (10.22) and the divergence of which forces ~ according to

(13.10.1) through (13.10.3). A similar interpretation applies to the mean po-

tential temperature (13.10.5), which is forced by the convergence of eddy heat

flux

q v' O'

-- = P0 9

(13.12)

13.1.2 Turbulent Diffusion

Reynolds decomposition provides a framework for describing how turbulent

motions interact with the mean flow. However, it offers little clue as to how

the turbulent fluxes of momentum and heat forcing the mean circulation can

be determined. The description for mean motion (13.10) can be closed only

by resorting to empirical or

ad hoc

relationships between the eddy fluxes and

mean fields.

The closure scheme adopted most widely is inspired by molecular diffusion,

which smooths out gradients. Although more complex, turbulence has a simi-

lar effect on mean properties. Figure 13.2 shows the evolution of a turbulent

spot that has been introduced into a uniform flow at large

Re.

Streaklines of

smoke captured by the spot are dispersed across the turbulent region, which

spreads laterally with distance downstream. Therefore, mean concentrations

inside the turbulent region decrease steadily and have progressively weaker

gradients. Turbulent dispersion is responsible for mean concentrations of pol-

lutants diminishing following the breakdown of the nocturnal inversion (Sec.

7.6.3) and for the expansion of buoyant thermals (Sec. 9.3).

Turbulent dispersion acts on all conserved properties and is, at least quali-

tatively, analogous to molecular diffusion. The eddy momentum flux can then

be expressed in terms of the gradient of mean momentum (13.6.7)

~" = PoKM 9

V ~, (13.13.1)

13.1 Description of Turbulence 411

Figure 13.2 Turbulent spot introduced into a laminar flow (from right to left) at

Re =

4.0 x 105. After Van Dyke (1982).

where the

eddy diffusivity

of momentum KM is an analogue of the kinematic

diffusion. As far as the boundary layer is concerned,

viscosity v for molecular " " 3

it suffices to consider mean motion that is horizontally homogeneous, in which

case horizontal diffusion of momentum vanishes and KM pertains to the ver-

tical flux alone. The vertical eddy flux of momentum

w'v' - -KM-~z

(13.13.2)

is then proportional to the vertical gradient of mean momentum. Likewise,

the vertical heat flux becomes

w' O' - -Ki_I-~z ,

(13.13.3)

where K/_/is the eddy diffusivity of heat.

Expressions (13.13) comprise the so-called

flux-gradient relationship.

Turbu-

lent transfer in (13.10) then assumes the form of diffusion of mean properties

(e.g., KMV2~). Eddy diffusivity, although it can be defined as above, depends

on the unknown fluctuating field properties. So, in practice, KM and K/_/must

be evaluated empirically in terms of the eddy fluxes w'u' and w'0'. Measured

eddy diffusivities range between 1 and 10 2 m e s -1 inside the boundary layer.

These values of KM are orders of magnitude greater than its counterpart for

molecular diffusion (v - 10 -5 m e s-l), which makes turbulent diffusion the

chief source of drag and mechanical heating exerted on the mean flow.

3For anisotropic turbulence (e.g., wherein statistical properties vary with direction) KM is a

tensor, the components of which refer to turbulent dispersion in the horizontal and vertical

directions; see Andrews

et al.

(1987) for applications to two-dimensional models.

412

13 The Planetary Boundary Layer

13.2

13.2.1

Structure of the Boundary Layer

The Ekman Layer

In terms of eddy diffusivity, the horizontal momentum equations inside a

boundary layer in which mean properties are steady and horizontally homo-

geneous become

1 O-fi

o~2-U

-f-~ = t- K~ (13 14.1)

PO cgX o~Z 2' " '

1 o~p o~2V

f-a = ~- K~ (13.14.2)

Po Oy

~Z 2'

where K = KM is regarded as constant and the Boussinesq approximation has

been used to ignore vertical advection of mean momentum. Eliminating the

pressure gradient in favor of the geostrophic velocity transforms (13.14) into

K02

O9Z2 q-

f(5-

l)g) - 0,

(13.15.1)

Oz e - f(-~- Ug)

= 0. (13.15.2)

Multiplying (13.15.1) by

i = ~/~-1

and adding to (13.15.2) results in the single

equation

d2X

K-~-ffz 2 - if)( = -ifXg

(13.16.1)

in terms of the consolidated variables

X = ~ + if, (13.16.2)

Xg -- Ugn t- iVg.

(13.16.3)

llg

does not vary through the boundary layer and is oriented parallel to the

x axis, (13.16) has the general solution

X(z) - A

exp[(1 +

i)yz] + B

exp[-(1 +

i)yz] + Ug

(13.17.1)

where

7= 2-K" (13.17.2)

The no-slip condition requires the horizontal velocity to vanish at the surface,

whereas the motion must asymptotically approach the geostrophic velocity

13.2

Structure of the Boundary Layer

413

above the boundary layer:

~=0 z =0,

(13.17.3)

Incorporating these boundary conditions and collecting real and imaginary

parts then yields the component velocities

g(z) - ug (1 - e -v~ cos

yz),

(13.18.1)

V(Z) -- Vge -Tz sin yz, (13.18.2)

which define an

Ekman layer.

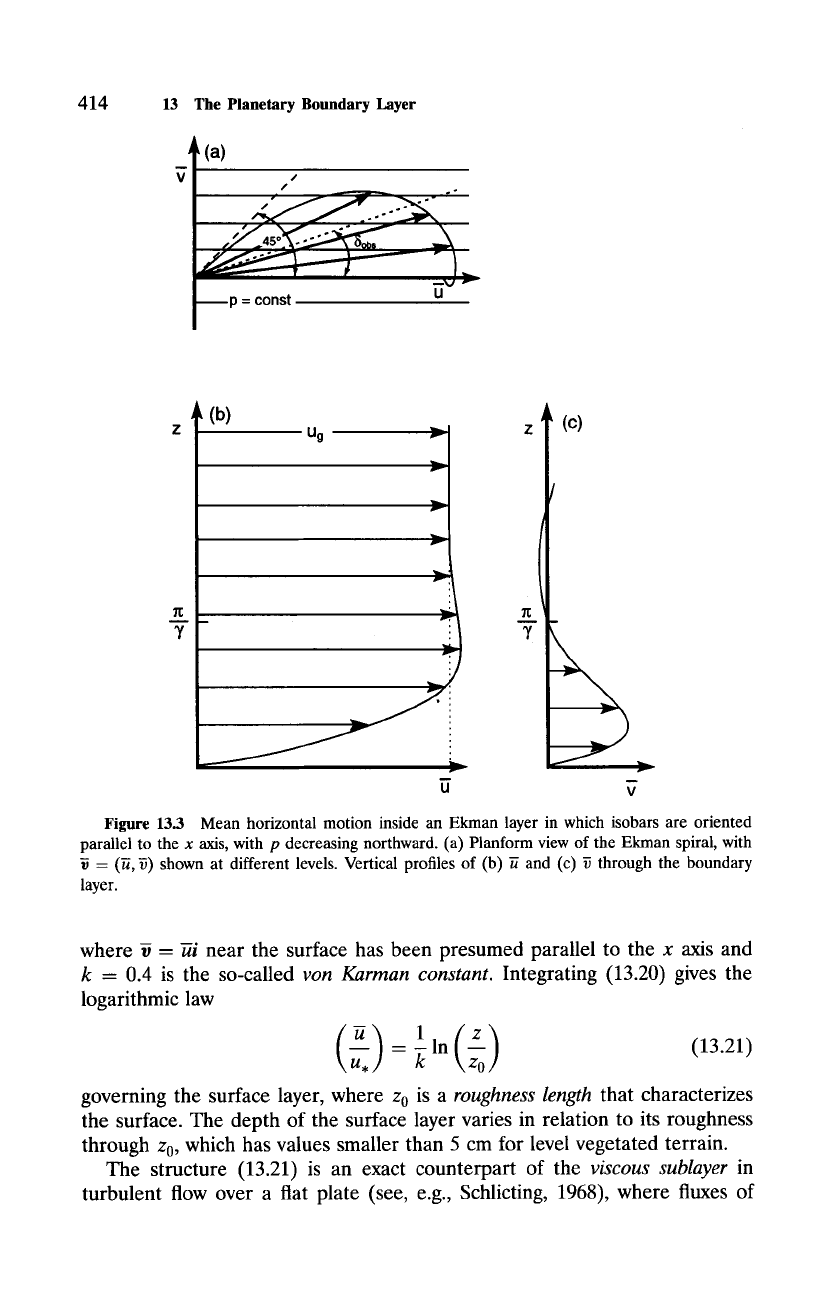
The mean velocity in (13.18) describes an

Ekman spiral,

which is plotted in

Fig. 13.3a as a function of height. Moving downward through the boundary

layer witnesses a rotation of the mean velocity, to the left in the Northern

Hemisphere and across isobars toward low pressure (Sec. 12.3), until a limiting

deflection 6 - 45 ~ is reached at the ground. The deflection from isobars is

an indication of turbulent drag exerted on the mean flow, which increases

with mean vertical shear (Fig. 13.3b) and drives the motion out of geostrophic

equilibrium. The effective depth of the Ekman layer is given by

7r/y,

where

reverses sign and above which ~ remains close to

(Fig. 13.3c). Values of

K - 10 m 2

S -1

and f-

10 .4 s -1

give

7r/y

~ 1 km. In practice, a pure Ekman

spiral is seldom observed. 4 Nonetheless, it captures the salient structure of the

planetary boundary layer, a deflection from surface isobars

6ob s "~

25 ~ being

typical.

13.2.2 The Surface Layer

Within the lowest 15% of the boundary layer, the assumption that K ~ const

breaks down. Instead, K, which is determined by the characteristic velocity

and length scales of turbulent eddies, varies linearly with height. In this re-

gion, the no-slip condition forces eddies to have a characteristic length scale

proportional to the distance z from the boundary and a characteristic velocity

scale

u, - (-u--~ ~ , (13.19)

which is known as the

friction velocity

because it reflects the turbulent shear

stress near the ground. The flux-gradient relationship (13.13) then requires

2 kzu, 0-~

u, - --, (13.20)

4The

high Re characteristic of the atmosphere makes simple Ekman flow dynamically unstable.

414 13 The Planetary Boundary Layer

~'l (a)

,, ,'

~p = const U

i~(b)

uQ ~!I

z (c)

-7- '

i n

u v

Figure 13.3 Mean horizontal motion inside an Ekman layer in which isobars are oriented

parallel to the x axis, with p decreasing northward. (a) Planform view of the Ekman spiral, with

= (~, ~) shown at different levels. Vertical profiles of (b) ~ and (c) ~ through the boundary

layer.

where ~ = ~i near the surface has been presumed parallel to the x axis and

k - 0.4 is the so-called yon Karman constant. Integrating (13.20) gives the

logarithmic law

(~__u,) 1 (z)_~ln ~00 (13.21)

governing the surface layer, where z 0 is a roughness length that characterizes

the surface. The depth of the surface layer varies in relation to its roughness

through z0, which has values smaller than 5 cm for level vegetated terrain.

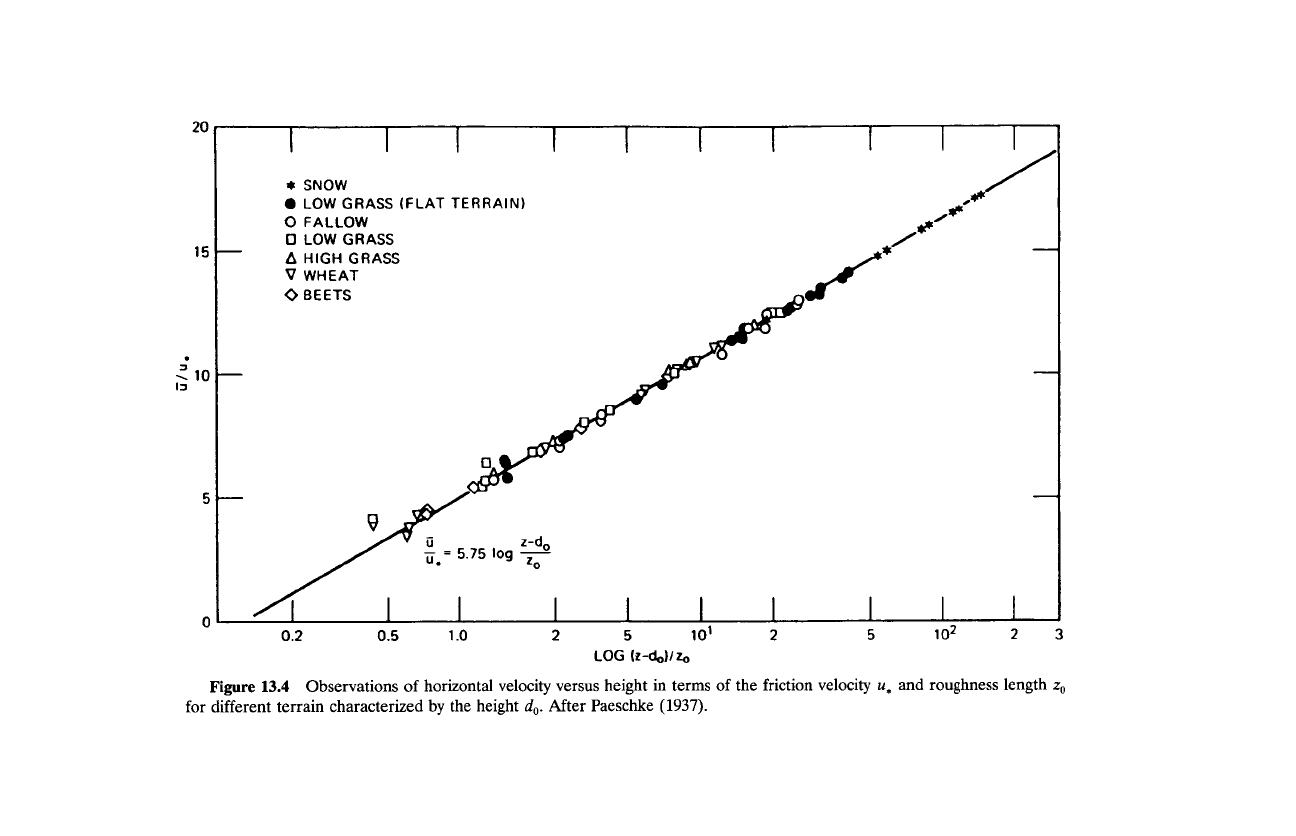
The structure (13.21) is an exact counterpart of the viscous sublayer in

turbulent flow over a flat plate (see, e.g., Schlicting, 1968), where fluxes of

13.3 Influence of Stratification 415

momentum and heat are independent of height. For neutral stability, the log-

arithmic behavior predicted by (13.21) is well-obeyed over a wide range of

level terrain (Fig. 13.4). The same is true for stable stratification, within some

distance of the surface.

13.3 Influence of Stratification

Under more general circumstances, static stability sharply modifies the char-

acter of the boundary layer by influencing the production and destruction of

turbulence. Vertical shear of the mean flow leads to mechanical production of

turbulent kinetic energy. Under neutral stability, that energy cascades equally

into all three components of motion. Turbulent kinetic energy is also pro-

duced through buoyancy. Contrary to mechanical production, buoyancy can

represent either a source or a sink of turbulent kinetic energy. Under unsta-

ble stratification, turbulent vertical velocities w' are reinforced by buoyancy,

whereas they are damped out under stable stratification. In either event, buoy-

ancy acts selectively on the vertical component of motion. Even though some

of that energy cascades into the horizontal components, buoyancy makes the

turbulent motion field anisotropic. In the presence of strong positive stabil-

ity, the vertical component may contain very little of the turbulent kinetic

energy.

The degree of anisotropy is reflected in the dimensionless

flux Richardson

number

g W f 0 /

= ~o~, (13.22)

which represents the ratio of thermal to mechanical production of turbulent

kinetic energy. Unlike other dimensionless parameters, Rf is a function of

position. Inside the surface layer, downward flux of positive x momentum,

which exerts drag on the ground, makes the denominator of (13.22) negative.

Under unstable stratification, the vertical heat flux must be positive to transfer

heat from lower to upper levels and drive the stratification toward neutral

stability (Sec. 7.5). Then

< 0. Large negative values of Rf, such as those

that occur in the presence of weak shear, imply turbulence that is driven

chiefly by buoyancy, which is termed

free convection.

If the heat flux vanishes,

= 0 and turbulence is driven solely by shear. Under stable stratification,

the vertical heat flux must be negative (Problem 13.12), so Rf > 0. Buoyancy

then opposes vertical eddy motions and damps out turbulent kinetic energy.

For turbulence to be maintained, production by shear must exceed damping

by buoyancy.

"nl n

SNOW

LOW GRASS (FLAT TERRAIN)

FALLOW

LOW GRASS

HIGH GRASS

WHEAT

BEETS

0.2

0.5

10’

102

LOG

k-&)/~

Figure

13.4

Observations of horizontal velocity versus height in terms of the friction velocity u, and roughness length

for different terrain characterized

the height

do.

After Paeschke

(1937).

13.3 Influence of Stratification 417

Analogous, but more readily evaluated, is the

gradient Richardson number

g o0

Ri - o oz

3-a] 2

3z]

N 2

= (o~2.

(13.23.1)

3z 1

With (13.13), the gradient Richardson number is related to the flux Richardson

number as

RZ - -~M Ri.

(13.23.2)

KM -- KH,

the two are equivalent. The gradient Richardson number reflects

the dynamical stability of the mean flow, so it provides a criterion for the onset

of turbulence. For

N 2 > O, Ri

is positive and buoyancy stabilizes the motion

by opposing vertical displacements. Disturbances having vertical motion are

then damped out if the destabilizing influence of shear in the denominator

is sufficiently small. Stability analysis (see, e.g., Thorpe, 1969) reveals sheared

flow to be dynamically unstable if

< ~. (13.24)

Supported by laboratory experiments (Thorpe, 1971), this criterion corre-

sponds to shear production of turbulent kinetic energy exceeding buoyancy

damping by a factor of 4. Small disturbances then amplify into fully developed

turbulence? Similar behavior occurs for

< 0, in which case turbulence is

1 small disturbances are damped out by

also driven buoyantly. For

Ri > ~,

buoyancy, so turbulence is not favored.

Stable stratification inhibits turbulence inside the boundary layer. But in-

creasing shear near the surface eventually makes mechanical production of

turbulent kinetic energy large enough to overcome damping by buoyancy.

Consequently, there inevitably exists a turbulent layer close to the ground in

which K varies logarithmically and fluxes of momentum and heat are indepen-

dent of height. The depth of this layer is controlled by surface roughness and

by stability. Strong stability limits the layer to a few tens of meters above the

ground, whereas weak stability allows a deeper layer with smaller

aft/Oz.

Strong surface heating, such as that occuring under cloud-free conditions or

over warm sea surface temperature (SST), favors buoyantly driven turbulence

5 Outside the boundary layer, the criterion for the onset of turbulence can be satisfied locally,

for example, in association with fractus rotor clouds (Fig. 9.22) and severe turbulence found in

the mountain wave (see Fig. 14.24).

Entrainment Zone

------

Layer

Free Convection

Superadiabatic Layer

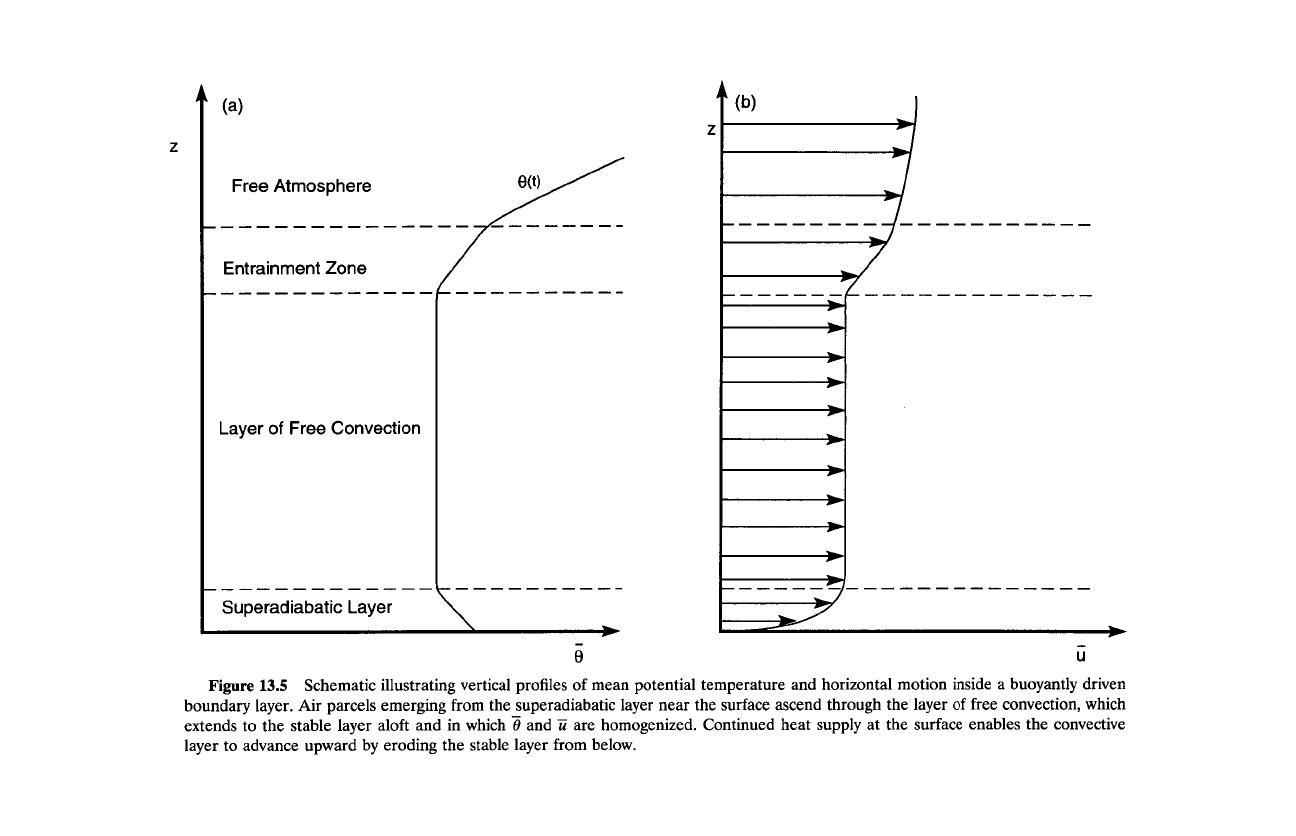
Figure

13.5

Schematic illustrating vertical profiles

mean potential temperature and horizontal motion inside

buoyantly driven

boundary layer. Air parcels emerging from the superadiabatic layer near the surface ascend through the layer

free convection, which

extends to the stable layer aloft and in which

and

are homogenized. Continued heat supply at the surface enables the convective

layer to advance upward by eroding the stable layer from below.

13.3

Influence of Stratification

419

2000

1800

1600

1400

"E" 1200

I'-

"1" 1000

u.I 800

600

400

200

I I I I

(a)

- 7:'

l,Y

_ 15.'~

I "

118

-f /

277 279 281 283 285 287 289 291

' ' ' /'t/

h r ..

i _

2000

1800

1600

1400

1200

1000

800

600

400

200

(b)'~i ' ' , , , , ,

9

- ~

":':'"~"~.. 15

12~. "'.

09~-

'1"

- ~t~

0 t

0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5

0 (K) q x 10 3

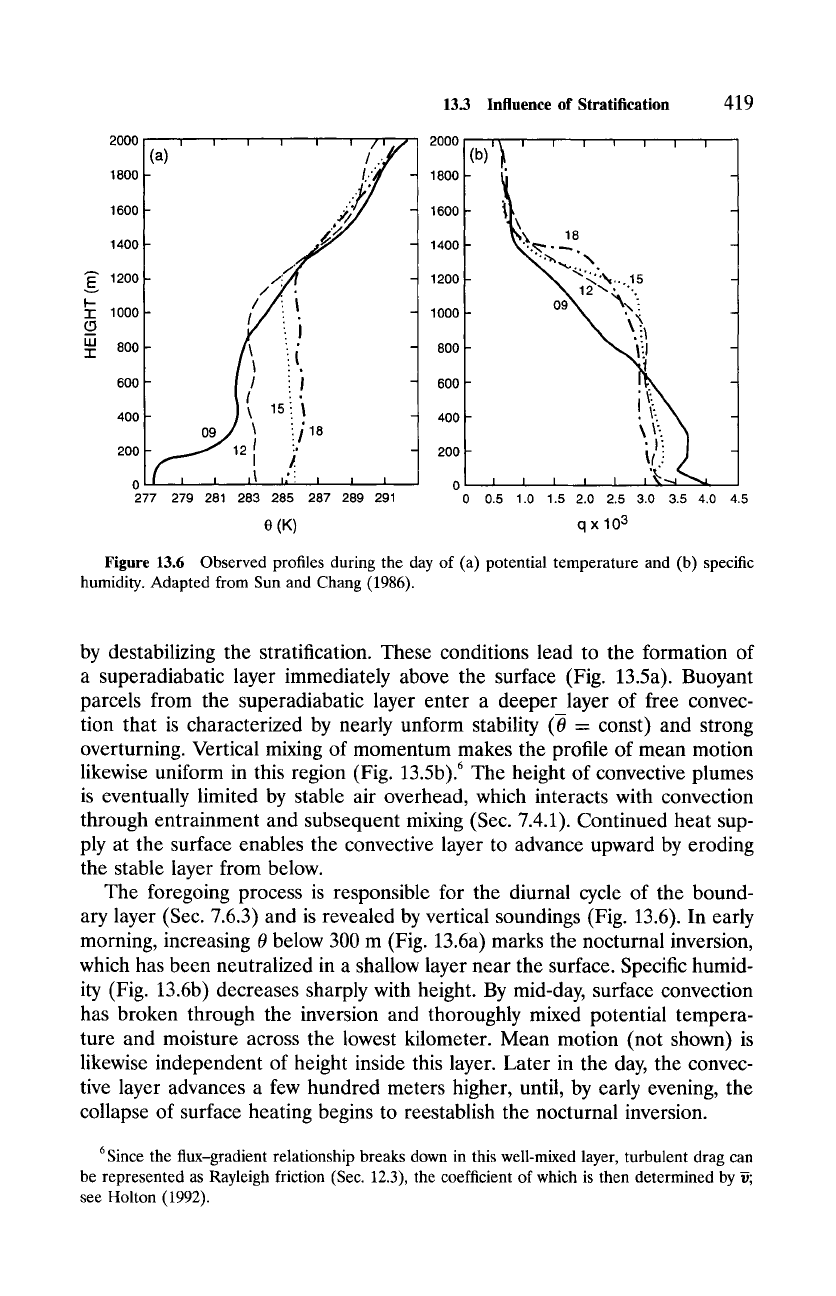
Figure 13.6 Observed profiles during the day of (a) potential temperature and (b) specific

humidity. Adapted from Sun and Chang (1986).

by destabilizing the stratification. These conditions lead to the formation of

a superadiabatic layer immediately above the surface (Fig. 13.5a). Buoyant

parcels from the superadiabatic layer enter a deeper layer of free convec-

tion that is characterized by nearly unform stability (0 = const) and strong

overturning. Vertical mixing of momentum makes the profile of mean motion

likewise uniform in this region (Fig.

13.5b). 6 The

height of convective plumes

is eventually limited by stable air overhead, which interacts with convection

through entrainment and subsequent mixing (Sec. 7.4.1). Continued heat sup-

ply at the surface enables the convective layer to advance upward by eroding

the stable layer from below.

The foregoing process is responsible for the diurnal cycle of the bound-

ary layer (Sec. 7.6.3) and is revealed by vertical soundings (Fig. 13.6). In early

morning, increasing 0 below 300 m (Fig. 13.6a) marks the nocturnal inversion,

which has been neutralized in a shallow layer near the surface. Specific humid-

ity (Fig. 13.6b) decreases sharply with height. By mid-day, surface convection

has broken through the inversion and thoroughly mixed potential tempera-

ture and moisture across the lowest kilometer. Mean motion (not shown) is

likewise independent of height inside this layer. Later in the day, the convec-

tive layer advances a few hundred meters higher, until, by early evening, the

collapse of surface heating begins to reestablish the nocturnal inversion.

6Since the flux-gradient relationship breaks down in this well-mixed layer, turbulent drag can

be represented as Rayleigh friction (Sec. 12.3), the coefficient of which is then determined by ~;

see Holton (1992).