Russ J.C. Image Analysis of Food Microstructure

Подождите немного. Документ загружается.

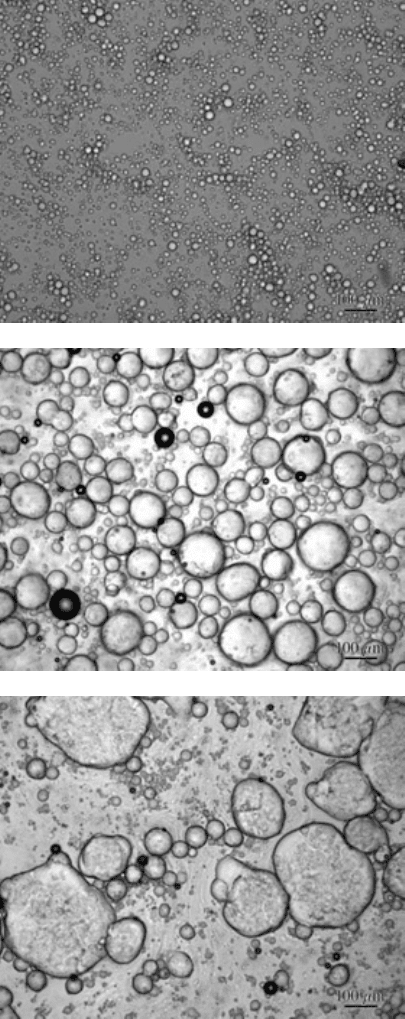
(a)

(b)

(c)

FIGURE 5.21

Fat droplets in milk: (a) after homogenization; (b) before homogenization; (c)

before homogenization, long standing time. (Courtesy of Ken Baker, Ken Baker Associates)

2241_C05.fm Page 307 Thursday, April 28, 2005 10:30 AM

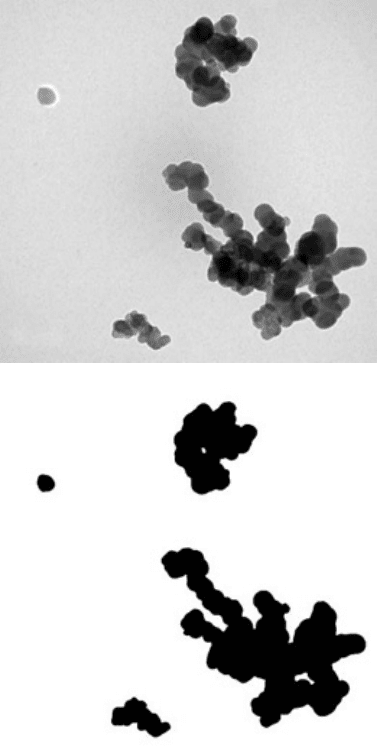
multiple images at high magniﬁcation (which will show the small features) and then

tile them together to produce a single large image in which the large features can be seen.

The images in Figure 5.21 raise another issue for feature measurement. Just

what is the size of a droplet? The dark line around each droplet results because the

index of refraction of light in water (the matrix) is not the same as in fat (the droplets).

Consequently, each droplet acts as a tiny lens and light that passes through the edge

of each droplet is directed away from the camera, producing the dark ring. The most

(a)

(b)

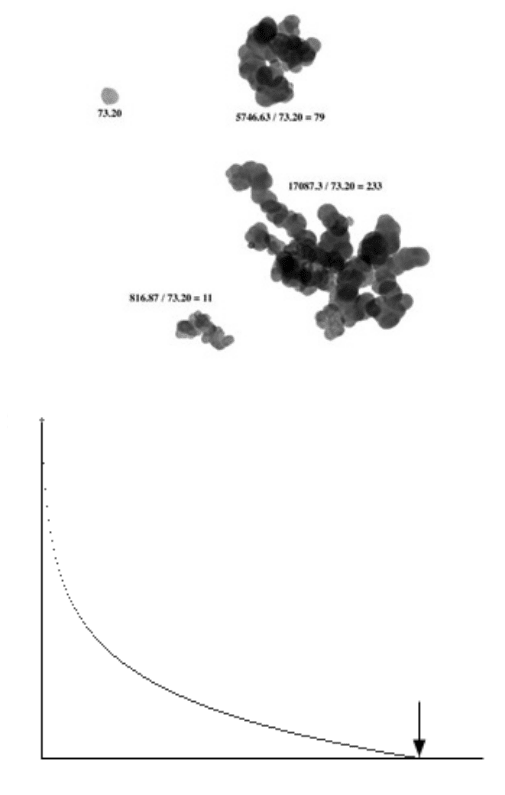
FIGURE 5.22 Using density to count particles in clusters: (a) original TEM image; (b) thresh-

olded to delineate the clusters; (c) combination of images (a) and (b) to delineate the clusters

with original grey scale values (labels give the integrated optical density and the estimated number

of particles); (d) Beer’s law calibration curve (the background point is set to the mean pixel

brightness of the background around the clusters, corresponding to no attenuation).

2241_C05.fm Page 308 Thursday, April 28, 2005 10:30 AM

convenient use of the dark outlines is to threshold them and ﬁll the interiors of the

droplets. That is correct for the case of fats in water. But for an emulsion of water in

fat, the dark line would surround the droplet rather than being part of it. In that case,

the procedure should be to threshold the dark line and process the image to keep the

interior but not the line. So some knowledge of the nature of the sample and the physics

of the generation of the image is needed to obtain accurate measurements.

Physics can be used to enable measurement in another situation that would other-

wise be difﬁcult, the case of a three-dimensional cluster of particles. In Figure 5.22

(c)

(d)

FIGURE 5.22 (continued)

816.87 / 73.20 = 11

17087.3 / 73.20 = 233

5746.63 / 73.20 = 79

73.20

1.0

Density (arbitrary units)

Background

= 219

0 255

Pixel brightness value

2241_C05.fm Page 309 Thursday, April 28, 2005 10:30 AM

several clusters of particles, all about the same size, are seen (along with one image

of a single particle). The projected area of each cluster can be measured, but is not

meaningful. If this were a two-dimensional sample with clusters, the ratio of the

area of the cluster to that of a single particle would provide a useful measure of the

number of particles present in each cluster. But for a three-dimensional cluster this

is not correct.

Physics describes the absorption of light (or any other radiation — the image is

actually an electron micrograph) by Beer’s law, an exponential attenuation of signal

with the mass of material through which it passes. So measuring the integrated

optical density (IOD) of each cluster and calculating the ratio of that value to the

IOD of a single particle (preferably after measuring several to get a good average)

will calculate the number of particles in each cluster.

Figure 5.22 shows the procedure. The original image is thresholded (based on

the uniformity of the background) to produce a binary representation of the clusters.

An opening was applied to remove isolated single-pixel noise. This binary image

was then combined with the original to erase the background and leave each cluster

with its original pixel grey scale values. A calibration curve was created using Beer’s

law of exponential absorption. The background point (zero optical density) was set

to the mean brightness level of the background. The vertical density scale is arbitrary

and does not require standards, since only ratios will be used.

The integrated optical density (IOD) of each cluster (and the single particle) is

determined by converting each pixel value to the corresponding density and summing

them for all pixels. The IOD thus represents the total absorption of radiation passing

through the cluster, which is proportional to the total mass (and thus to the total

volume) of material present. Dividing the IOD for each cluster by that for a single

particle calculates the number of particles present in the cluster. Of course, this

method only works if the cluster is thin enough that some signal penetrates com-

pletely through each point. If the attenuation is total so that a pixel becomes black,

then more mass could be added without being detected.

Generally, this method works best with images having more than 8 bits of

dynamic range. An optical density of 4 (the range that can be recorded by medical

X-ray ﬁlm) corresponds to attenuation values up to 99.99% of the signal, recording

a signal of one part in 10,000. A camera and digitizer with 13 bits of dynamic range

can capture a variation of one part in 8192, while 14 bits corresponds to one bit in

16,384. Cameras with such high bit depth are expensive, require elaborate cooling,

and are generally only used in astronomy. A high-end, Peltier cooled microscope

camera may have 10 or 12 bits of dynamic range (approximately one part in 1000

to one part in 4000).

BRIGHTNESS AND COLOR MEASUREMENTS

This foray into particle counting has brought us again to the measurement of

brightness and/or color information from images. The example in Figure 5.10

showed counting of features based on their color signature. The example in Figure

5.22 showed the use of integrated optical density measurement for each feature (each

cluster) to determine the number of particles contained within the feature. In general,

2241_C05.fm Page 310 Thursday, April 28, 2005 10:30 AM

density measurements are used to measure total mass. In the example of Figure 5.23,

an image of frog blood cells shows dark nuclei and less dense cytoplasm. Because

each cell has settled into a size and shape that only partly depends on its contents,

and partly on its surroundings, measuring the area of each feature does not produce

as useful a result as measuring its volume. This three-dimensional property can be

obtained from the optical density measurement.

The cells in the original image touch each other. Rather than watershed segmen-

tation, another procedure was used in this example. Each cell has a well deﬁned,

dark nucleus. These were thresholded and the image inverted so that the background

could be skeletonized. The skeleton of the background is called the “skiz” and

provides lines of separation that bisect the distance between features. Erasing the

pixels along the skiz lines from the thresholded image of the entire cells separates

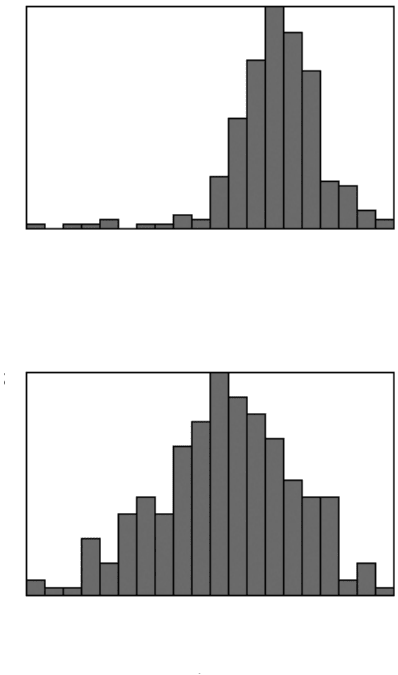
them so they can be measured individually. The distribution plot of cell areas has a

very different appearance from that of the cell integrated density values, which more

accurately reﬂect the total cell volumes.

In many cases the density values, either calibrated as optical density or simple

uncalibrated pixel brightness numbers, are used to measure proﬁles along lines across

(a) (b)

FIGURE 5.23 Measurement of density to determine volume: (a) original image of cells; (b)

thresholded nuclei; (c) skeleton of the background (the skiz); (d) cells separated by erasing

the skiz; (e) cell area distribution; (f) cell density distribution (arbitrary units).

2241_C05.fm Page 311 Thursday, April 28, 2005 10:30 AM

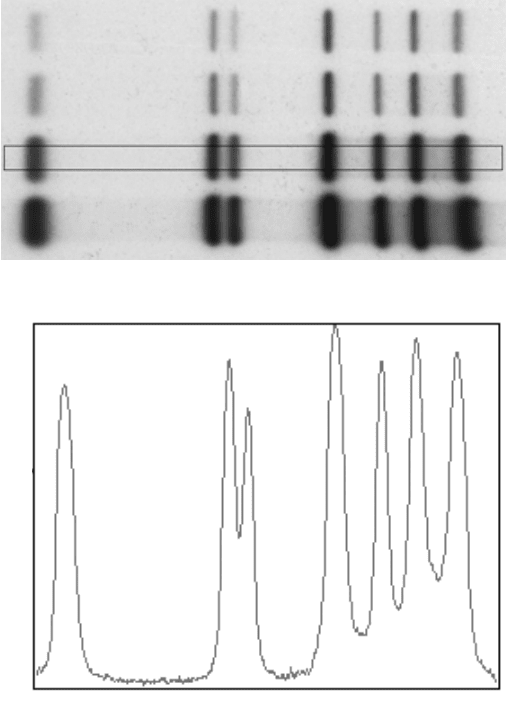
the image. Figure 5.24 shows a typical example, measuring the density along a

column in an electrophoresis separation of proteins. The values are averaged in the

vertical direction at each horizontal point within the marked column, and the average

intensity, usually converted to optical density, is plotted as shown. Analysis is then

performed on the one-dimensional plot using peak ﬁnding software.

In many cases a plot of intensity is an effective way to extract information in a

way that simpliﬁes measurement. Growth rings in plants (Figure 5.25) provide a

representative example.

Plots of color values can also be used in many cases to simplify measurement

of dimensions. In the example of Figure 5.26, determining the thickness of the crust

on the bread could be performed by a complicated procedure of thresholding and

applying morphological operations to delineate a boundary, using a Boolean AND

to apply a grid of lines, and then measuring the line lengths. It is much more efﬁcient

(e)

(f)

FIGURE 5.23 (continued)

Min = 701 Area (pixels) Max = 2343

To tal = 232, 20 bins

Mean = 1808.74, Std. Dev. = 224.391

Skew = 1.44688, Kurtosis = 7.97697

Count

Min = 114.8 Density Max = 151.5

To tal = 232, 20 bins

Mean = 134.689, Std. Dev. = 7.00476

Skew = –0.27632, Kurtosis = 2.59955

Count

2241_C05.fm Page 312 Thursday, April 28, 2005 10:30 AM

to plot the average proﬁle in a broad band perpendicular to the edge of the slice.

There is a deﬁnite change in color associated with the crust, and it is (as usual) more

effective to work with the hue, saturation and intensity values than with red, green,

and blue. In the example, the hue is virtually unchanged, and the intensity changes

only slightly at the boundary of the crust, reﬂecting primarily the presence of open

cells in the bread. However, the saturation drops abruptly when the crust gives way

to the interior bread structure, and provides a quick, effective and reproducible

measurement of the dimension.

Calibrating the intensity vs. concentration for ﬂuorescence images can be difﬁ-

cult, but in many cases can be avoided by instead using ratios of the intensity at two

(a)

(b)

FIGURE 5.24 Plotting a density proﬁle: (a) one column in a scanned image of protein bands

separated by gel chromatography; (b) the resulting density plot.

Distance

Density

2241_C05.fm Page 313 Thursday, April 28, 2005 10:30 AM

different wavelengths of excitation, or two different emission wavelengths. Ratios

of the intensity above and below the absorption edge energy of a dye, for example,

provides a direct measure of the amount of the ﬂuorescing material at each location.

Figure 3.47 in Chapter 3 illustrates that process for a Fura stain that localizes calcium

activity.

FIGURE 5.25 Growth rings in a ﬁr tree can also be measured by plotting an intensity proﬁle.

FIGURE 5.26 (See color insert following page 150.) Measuring the thickness of a surface

layer (crust on bread) by plotting averaged pixel values. The saturation data are more useful

than intensity or hue in this example.

Profile

Scan

Region

Intensity

Saturation

Hue

2241_C05.fm Page 314 Thursday, April 28, 2005 10:30 AM

When two (or more) different dyes or stains are present, recording their emis-

sions in different color channels is often used to produce color representations of

the structure. Figure 2.15 in Chapter 2 shows a typical example. In a color image

produced by recording different images in the red, green, and blue color channels,

the co-localization of stains is indicated by color shifts or the presence of mixed

colors such as magenta or yellow. A more quantitative approach to co-localization

can be obtained by plotting the intensity values of the channels at each pixel in the

image, as shown in Figure 5.27. The example in this case uses X-ray maps from an

SEM, indicating the distribution of speciﬁc elements in the sample. Clusters in the

plot represent pixels with various ratios of the two intensities, indicating the probable

presence of structures or phases with unique chemical signatures.

(a) (b)

FIGURE 5.27 Co-localization plots: (a) Si X-ray map; (b) Al X-ray map; (c) co-localization

plot. The four numbered clusters in the co-localization plot correspond to regions numbered

on the diagram (d).

Channel 1 intesity (Al)

Channel 2 intensity (Si)

2241_C05.fm Page 315 Thursday, April 28, 2005 10:30 AM

LOCATION

The location of features can be speciﬁed in several ways. The absolute coordi-

nates of the feature may be given in terms of distance from one corner of a slide or

mounting grid, or as the position of the microscope stage X- and Y- drives. This is

akin to using latitude and longitude as a way to describe position. For some purposes

it is very useful, but in others it is more interesting to know the distance and direction

from other features in the image. These in turn may either be similar features or

other structures present such as cell walls or boundaries. Examples in Chapter 4

showed how the Euclidean map could be used to measure distance from boundaries,

for instance.

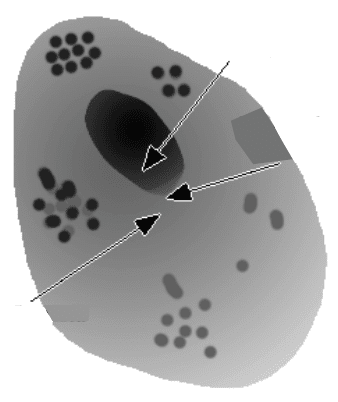
Another issue that arises in specifying the position of a feature is just what point

within the feature should be used for measurement. There are several possible

choices, as shown in Figure 5.28. The centroid of a feature is the point at which it

would balance if cut from uniform thickness cardboard, and this is one of the most

widely used location parameters. But for a feature like a cell in which density varies

from place to place (as discussed above, it typically measures local mass thickness),

the density-weighted centroid may be a more logical choice. The geometric center

can be speciﬁed in several ways, the most robust of which is the center of the

circumscribed circle around the feature. Another possible location point is the ulti-

mate eroded point from the Euclidean distance map; this is the center of the largest

inscribed circle in the feature. For most features these points will not be in the same

location and their measurement may lead to different interpretations of spatial

distribution. If the features are symmetrical, such as spherical droplets, the points

are all in the same place.

FIGURE 5.28 The location of a feature can be speciﬁed in several ways.

Density-weighted

Centroid

Geometric

Center

Centroid

2241_C05.fm Page 316 Thursday, April 28, 2005 10:30 AM