Russ J.C. Image Analysis of Food Microstructure

Подождите немного. Документ загружается.

dilated to 3 pixels thick so that they show up better in the book. For measurement

purposes, they would all be just one pixel wide, and connected as shown in Figure

4.29. The skeleton lines are eight-connected, meaning that they are continuous lines

in which a pixel is understood to touch any of its eight possible neighbors. That is

also the most common convention for deciding that pixels touch each other to form

a connected object. But if an image with an eight-connected skeleton is inverted, so

that the cells become features, they are not separated. The pixels in the cells also

touch at the corners and cross the skeleton lines. In general, if an eight-connected

rule is used for pixels in features, then a four-connected rule (pixels touch only if

they share a common side, not just a corner) must be adopted for the background.

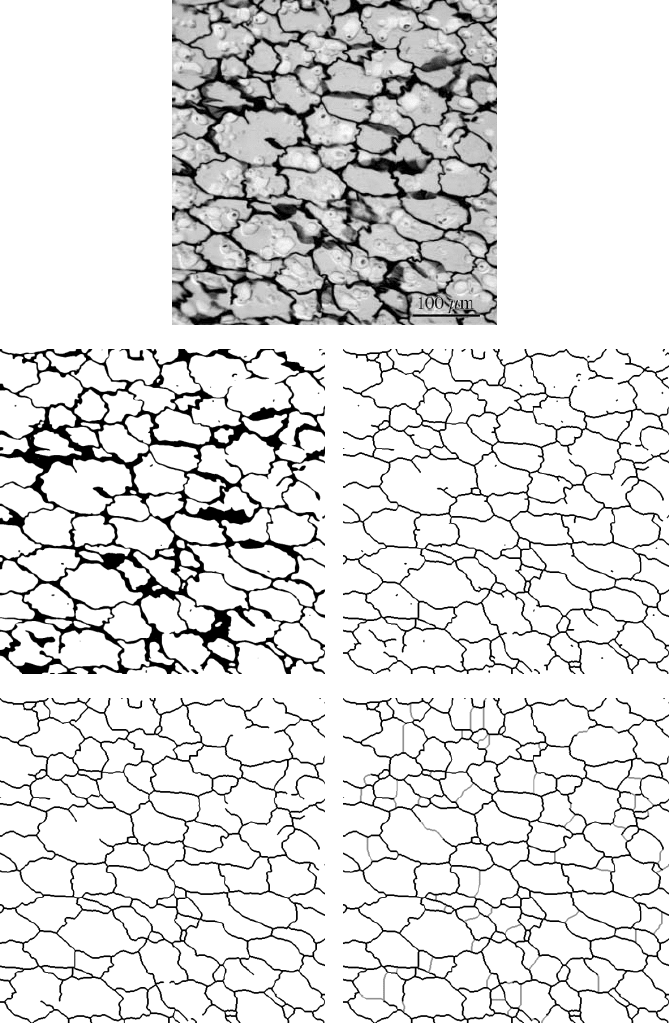
In the example of Figure 4.31, a section through potato shows broad cell walls

because of the ﬁnite thickness of the section and the angles of the walls. In the

thresholded image (from the red channel of the original color image), the broad

walls and some extraneous dark specks complicate measurement. Skeletonization

reduces the walls to lines, and discarding any terminal branches (ones that have end

points) and are short (in the example, less than 20 pixels) or lines that are not a part

of the continuous tessellation, cleans up the image.

There are still some breaks in the tessellation that may or may not be real, and

which can be seen to correspond to gaps in the original image. If the breaks are due

to inadequacies of preparation, then completing the tessellation by ﬁlling in the gaps

is legitimate. Rather than drawing them in by hand, an automatic method that works

well if the cells are convex is to invert the image and apply a watershed segmentation

to the interiors of the cells. As shown in Figure 4.31(e), this ﬁlls in the gaps, but in

this case also subdivides a few of the cells that have shapes that are narrow in the

center.

Skeletonization of a cell image allows measurement of several characteristics

that are often important descriptors of the three-dimensional structure and relate to

its macroscopic properties. As an example of the use of the skeleton for a cell

structure, Figure 4.32 shows cross-sections (at the same magniﬁcation) through

apples which are characterized by a sensory test panel as having ﬁrm, medium, and

soft textures.

In order to correlate structural properties with sensory parameters, the images

were thresholded and skeletonized. The principal difference between the ﬁrm and

medium apples is in the scale of the network structure. The node density in the ﬁrm

apples is 1.72 per 10,000 µm

, and this drops to 1.25 for the medium apples. The

simple coarsening of the structure allows greater compliance and can account for

the change in sensory perception. The structure of the soft apples is quite different.

The presence of a few large open spaces allows much more deformation before

fracture when the apple is bit into. From a measurement standpoint, the distribution

of lengths of the skeleton branches is very different for soft apples. The mean value

doubles and the standard deviation quadruples compared to the ﬁrm apples, while

the statistical kurtosis and appearance of the distribution suggests that a duplex

structure with two sizes of structure has formed. There may be other differences

between these apple varieties as well (for instance, the area or intercept length of

the sections through the cells will show a similar trend), but the ability of simple

microstructural measurements to support sensory experience is interesting.

2241_C04.fm Page 256 Thursday, April 28, 2005 10:29 AM

(a)

(b) (c)

(d) (e)

FIGURE 4.31 Editing the skeleton: (a) section of potato (red channel) showing cell walls; (b)

thresholded binary; (c) skeletonized; (d) elimination of short terminal branches and disconnected

segments; (e) ﬁlling in of additional lines by applying a watershed to the inverse image.

2241_C04.fm Page 257 Thursday, April 28, 2005 10:29 AM

(a) (b)

(e) (f)

FIGURE 4.32 Correlation between structure and sensory perception in apples: (a, c, e) cell

structure in ﬁrm, medium and soft apples; (b, d, f) skeletonized structure measured as

discussed in text. Magniﬁcation marker is 500 µm. (Source: P. Allan-Wojtas, K. Sanford, K.

McRae, and S. Carbyn, An Integrated Microstructural and Sensory Approach to Describe

Apple Texture, Journal of the American Horticultural Society,128(3), 381–390, 2003. Repro-

duced with the permission of the Ministry of Agriculture and Agri-Food, Canada.)

2241_C04.fm Page 258 Thursday, April 28, 2005 10:29 AM

(a)

(b)

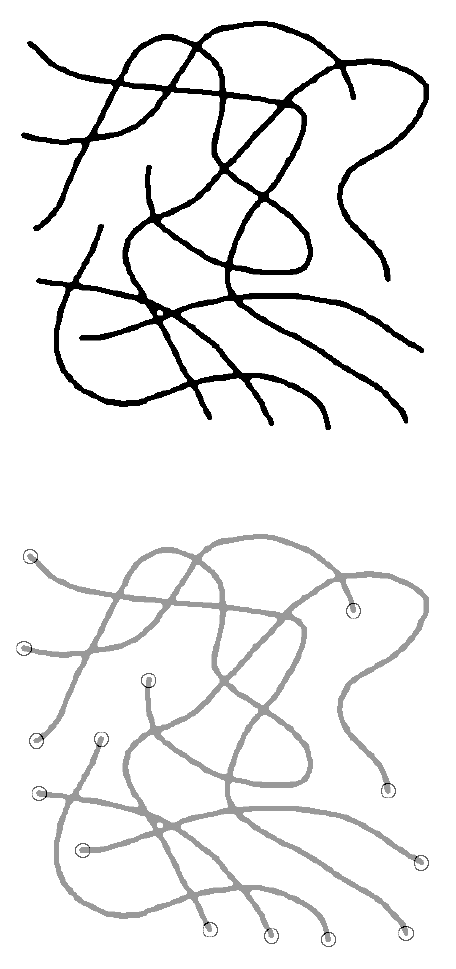
FIGURE 4.33 Example of an image with crossing ﬁbers: (a) binary image; (b) end points

marked using skeleton (there are 14 end points, corresponding to 7 ﬁbers, and the total length

of lines in the skeleton is 21 inches, so the average ﬁber length is 3 inches).

2241_C04.fm Page 259 Thursday, April 28, 2005 10:29 AM

FIBER IMAGES

Skeletonization is also used with ﬁber images, because it simpliﬁes counting and

measurement. In the example image of Figure 4.33, even a few crossing ﬁbers are

visually difﬁcult to count. Counting the end points (with one neighboring pixel) in

the skeleton of the ﬁbers gives a direct ﬁber count because each ﬁber has two ends.

Measuring the total length of the skeleton lines and dividing by the number of ﬁbers

(half the number of ends) gives the average ﬁber length, without any need to

disentangle the crossing features. (In the few instances in which measurement of

individual crossing ﬁbers is really necessary, the skeleton also plays a role. Finding

and removing all of the crossing points — pixels with more than two neighbors —

isolates the segments of the ﬁbers so they can be individually measured. Applying

logic to match up the segments based on their having end points that lie close together

and similar orientations allows adding together the pieces of each ﬁber to get the

overall length. This is a very specialized process, which is only rarely employed.)

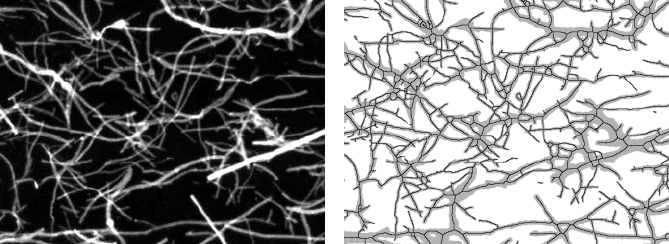
In a more complex ﬁber image such as the network of cellulose ﬁbers in Figure

4.34, the same technique of counting ends still works to determine the number and

total length of ﬁbers per unit area. If a ﬁber has only one end in the image ﬁeld, it

is counted as one-half ﬁber. That gives the correct number per unit area because the

other half would be counted in an adjacent ﬁeld of view. A few end points may be

missed if ﬁber ends lie exactly on other ﬁbers, but that is primarily a matter of

choosing the proper image magniﬁcation.

In a branching structure, the individual segments may be of interest (for example

to measure their length, orientation, etc.). Skeletonization followed by eliminating

the nodes or branch points disconnects all of the segments so that they can be

measured as individual features. In the example of Figure 4.35, the root structure

of a soybean seedling has been captured by spreading out the roots on a ﬂatbed

(a) (b)

FIGURE 4.34 More complex ﬁber image: (a) original grey scale image of cellulose ﬁbers;

(b) skeleton superimposed on binary image (measurement of the skeleton reports 174 end

points and 48 inches of total length in an area of 3 square inches).

2241_C04.fm Page 260 Thursday, April 28, 2005 10:29 AM

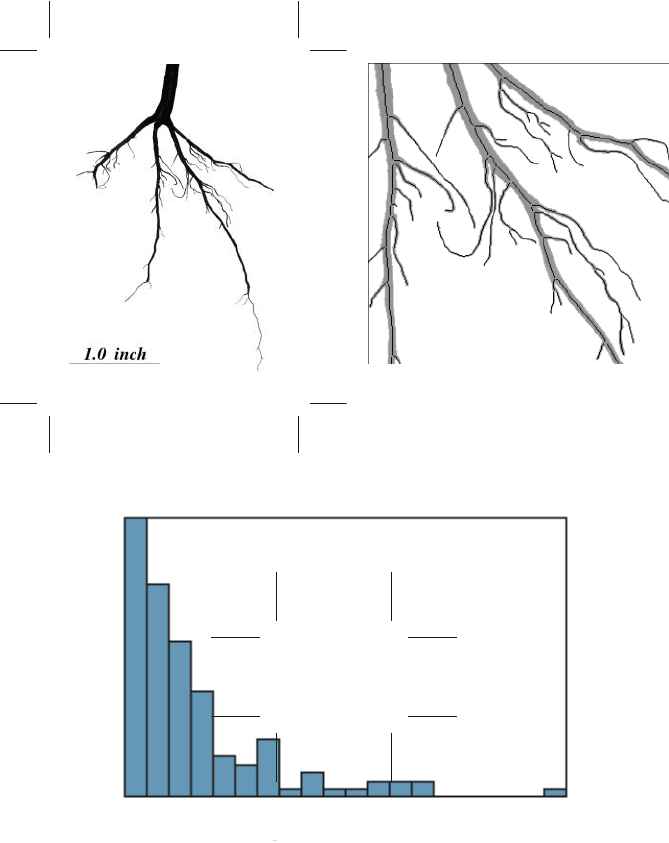
scanner. Thresholding, skeletonization, and removal of the points with more than

two neighbors, leaves the individual branches in the root structure. In a healthy plant

with adequate moisture and soil nutrients, a distribution with more uniform lengths,

rather than a few long and many very short branches, would be expected.

(a) (b)

(c)

FIGURE 4.35 Disconnecting skeleton segments: (a) original image of plant root; (b) enlarged

detail of skeleton with nodes removed, allowing measurement of individual segments; (c)

length distribution of segments.

To tal = 121

Mean = 0.14000

Std.Dev. = 0.14664

Min = 0.00664 Max = 0.84536

Length (in.), 20 bins

Number of Segments

2241_C04.fm Page 261 Thursday, April 28, 2005 10:29 AM

SKELETONS AND FEATURE SHAPE

The skeletons of individual features provide basic topological (shape) informa-

tion, which will also be used in the next chapter in the discussion of feature

measurements. Figure 4.36 shows that the number of end points in the feature

skeleton corresponds to the number of points in each star, which is the most recog-

nizable shape characteristic to a human observer.

In a more complex image, the visual recognition of properties such as the number

of arms, or the length of the arms, may be more difﬁcult for a person to recognize.

But the computer can do so easily using the same properties of the feature skeleton.

In the example of Figure 4.37, selection of the features with exactly six arms, or

with medium-length external branches (ones that end in an end point as opposed to

extending between two nodes in the structure) is illustrated. Combining these two

images with an AND selects features that meet both criteria.

FIGURE 4.36 Skeletons of some simple shapes superimposed on the original features. The

number of end points in each skeleton measures the basic topological information (number

of arms) that is recognized by human vision.

2241_C04.fm Page 262 Thursday, April 28, 2005 10:29 AM

MEASURING DISTANCES AND LOCATIONS

WITH THE EDM

In the preceding example, another variation present for the various irregular stars

is the width of the arms. Measuring the width of an irregular feature is often desired,

and sometimes cannot be handled well using a grid. In the example of Figure 4.19

a vertical line grid was appropriate because the thickness of the coating was implic-

itly deﬁned in that direction. But for the cross-section of the vein in Figure 4.20 the

radial lines do not really measure the desired dimension, and for a general, arbitrary

shape such as that shown in Figure 4.38, no ﬁxed grid can be devised that would

be useful.

(a) (b)

FIGURE 4.37 Feature selection using the skeleton: (a) hand-drawn star patterns; (b) features

with exactly six ends; (c) features with medium length arms; (d) Boolean AND combining

(b) and (c).

2241_C04.fm Page 263 Thursday, April 28, 2005 10:29 AM

The EDM provides a way to measure the width of such irregular shapes. The

distance map values increase from each edge and reach a maximum at the center of

the feature, which appears as a ridge line if the EDM is rendered as a surface. The

value of the EDM at each point along this line is the radius of an inscribed circle

at that location, and so measures the half-width of the feature at that point. Collecting

all of the EDM values along the center line thus permits the measurement of the

mean, variation (e.g., standard deviation), minimum and maximum widths of the

feature.

(a) (b)

FIGURE 4.38 Measurement of the width of an irregular feature: (a) example feature; (b)

Euclidean distance map; (c) skeleton with EDM values assigned to pixels; (d) histogram of

values in the skeleton. The minimum width of the feature is 34 (the lowest non-zero point

on the histogram is 17, which is the radius of the inscribed circle) and the maximum is 88

(the highest non-zero point on the histogram is 44). The mean width is 65.5 ± 13.1 (twice

the mean radius of 32.73 ± 6.55).

15 20 25 30 35 40 45 50

Radius (pixels)

100

120

Number (pixels)

2241_C04.fm Page 264 Thursday, April 28, 2005 10:29 AM

The skeleton marks the midline of the feature, so it can be used to collect the

desired EDM values, as shown in the ﬁgure. One way to accomplish this is to

duplicate the image, calculate the EDM of one copy and the skeleton of the second,

and then combine them arithmetically keeping whichever pixel value is lighter. All

pixels other than the skeleton are erased to white (background) while the EDM

values replace the black of the skeleton pixels. A histogram of the image (ignoring

all of the white background pixels) can be analyzed to perform the measurement.

Using the same procedure on the image from Figure 4.37, the features can be

grey-scale labeled to indicate the mean width of their arms as shown in Figure 4.39.

This adds another criterion by which they may be distinguished and sorted.

This measurement technique is particularly useful for characterizing the width

of irregular structures seen in cross section as shown in Figure 4.40. It must be

remembered that it is a two-dimensional measurement, and does not replace the use

of random line intersections as a tool for measurement of the true three-dimensional

thickness of layers sectioned at random orientations.

The location of features within cells, organs, or any other space, can also be

measured using the EDM. For a regular geometric shape such as a square or circle,

calculation of the distance of a feature from the boundary can be performed using

analytical geometry. For a typical irregular shape, this method cannot be used, but

the EDM can. Assigning the distance map value to each pixel within the cell or

region provides a measurement tool for any shape. Combining the EDM values with

an image of the centroid location of each feature, as shown in Figure 4.41, allows

the distance of each feature from the boundary to be measured using the grey scale

value (which can, of course, be calibrated in distance units rather than density).

In the example, the protein and starch granules were thresholded in one copy

of the image and the centroid feature of each marked (the ultimate eroded points

could also be used; in this example with convex features the difference is unimpor-

tant, but for irregular shapes the centroid may not lie within the feature, and the

ultimate eroded point may be preferred). A second copy of the image was thresholded

for the cell walls, which were then skeletonized and the image inverted so that the

FIGURE 4.39 The illustration from Figure 4.37(a) with features shaded according to the

width of the lines.

2241_C04.fm Page 265 Thursday, April 28, 2005 10:29 AM